基于MLS拟合带容差的测量数据加工刀位面生成算法
李向佳 戴 宁 廖文和 郭保苏 王永波
1.南京航空航天大学,南京,210016 2.山东新华医疗器械股份有限公司,淄博,255086
基于MLS拟合带容差的测量数据加工刀位面生成算法
李向佳1戴宁1廖文和1郭保苏1王永波2
1.南京航空航天大学,南京,2100162.山东新华医疗器械股份有限公司,淄博,255086
传统的刀位面生成算法无法直接生成存在缺陷的离散数据的刀位面,因此,针对球头铣刀提出了一种基于MLS拟合带容差的离散数据加工刀位面生成算法。该方法首先依据球头铣刀构造离散数据的点膨胀球模型,然后根据凸包原理获取该模型的最外层包络面,最终通过MLS投影拟合方法剔除奇异点、修补裂缝,生成刀位面网格模型。实例表明,该算法具有较高的稳定性,能够有效解决存在缺陷的离散数据刀位面生成问题,适用于实际工程应用加工。
移动最小二乘法;容差;测量数据;数控加工;刀位面
0 引言
CAD/CAM系统中,离散数据可以是由测量仪器直接获得的点云数据,也可以是由网格重构算法生成的多边形模型,即三角网格或四边形面片模型[1]。受到物理模型曲面的质量、复杂度以及测量仪器精度的影响,工程人员获得的点云数据可能存在细节缺失,并且这些缺失的细节会以裂缝的形式存在于待加工模型的表面。与点云数据相比,网格重构后的多边形模型虽然具有一定的拓扑连接关系,但模型表面会产生一些细小的裂缝和非二维流形奇异点。加工过程中,这些裂缝和非二维奇异点会使加工刀具行走路线出现偏差,在一定程度上造成刀具和机床的震动和磨损,严重影响模型的加工质量和效率。所以传统加工方法需要输入高质量无缺陷的离散数据模型才能正常完成模型加工。
传统加工离散数据的主要策略为:①获取离散数据的刀位面;②依据加工要求,在生成的刀位面上规划相应的刀具轨迹;③进行干涉检查和坐标转换,生成加工代码,完成离散数据的加工[1-2]。离散数据生成刀位面的方法主要有刀触点反算刀位点法和基于偏距原理法。由于球头刀有效切削区域为半球体,所以国内外学者多采用偏距原理生成离散数据的刀位面[3]。Choi等[4-5]提出了一种基于布尔运算的刀位面生成方法,该方法虽然实现了加工曲面和刀具反向扫掠曲面的布尔运算,生成离散数据的刀位面,但大量布尔操作增加了该算法的时间和空间复杂度。Jun等[6]基于三角面片法矢生成网格模型的刀位面,该方法原理简单,但为了构建完整封闭的刀位面模型,需要对三角面片偏移产生的断裂和自交进行延伸和裁减,增加了算法的计算时间。Ren[7]对上述算法进行了拓展,构建了适用于APT(automatically programmed tools)刀具的GCL-surface(general cutter location-surface)。由于该算法仍然需要进行上述后续操作,所以不适用于复杂的离散数据加工。为了避免后续繁杂的修复,Kim等[8]利用网格顶点对应的多重向量生成离散数据的刀位面,提出了适用于APT刀具刀位面的生成方法。但该算法适用性较差,当刀具半径较大时,模型内部存在自交。赵巍等[9]提出的基于特征点的离散偏距算法完善了上述算法。虽然减少了模型内部的自交,但该算法稳定性不足,不适用于生成离散数据的刀位面。Chen等[10]通过采样离散数据3个坐标方向的数据,构造LDNI(layered depth-normal images)-model,通过点的滤除器较好地去除了刀位面内部的自交,适用模型较为广泛。
上述传统的刀位面生成方法都需要输入没有缺陷的离散数据文件,对于一般存在缺陷的离散数据生成的刀位面质量不佳。缺陷数据需要事先编辑,检索出存在裂缝或非二维流形奇异点的区域,通过软件进行修补以达到光滑无空洞的要求。如果存在容差无自交的刀位面生成算法,则可以省去上述繁琐的预处理过程,直接生成符合工程实际应用的刀位面数据,提高离散数据加工范围和加工质量。所以本文提出了一种基于移动最小二乘法(moving least squares,MLS)拟合带容差的离散数据数控加工刀位面生成方法。
1 基于MLS拟合的离散数据刀位面生成方法概述
1.1离散数据数控加工刀位面的定义
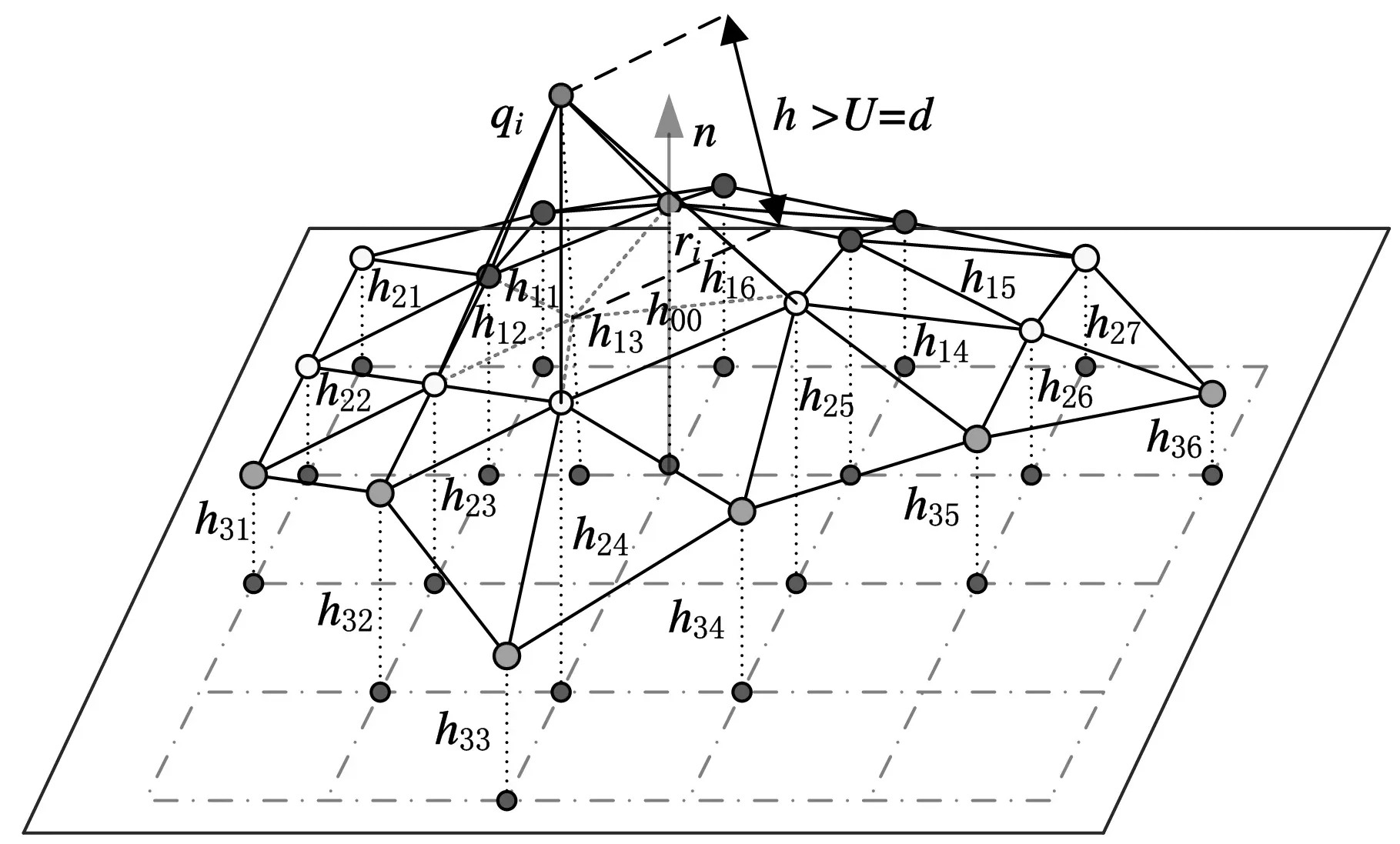
球头铣刀加工精度高、刀具寿命长,离散数据模型数控精加工常采用该类铣刀。球头铣刀的刀位点可以是刀具的几何中心,也可以是刀具的尖点。本文将球头铣刀刀具的几何中心视作刀具的中心点,加工刀具中心点所在的平面自然构成了加工刀位面[11]。因为刀具正向加工刀位点扫掠的曲面和刀具沿着加工曲面反向扫掠曲面重合[12],且球头铣刀有效切削区域为半球体,所以可以通过偏距球头刀半径大小的距离来获得离散数据多轴数控加工的刀位面,如图1所示。
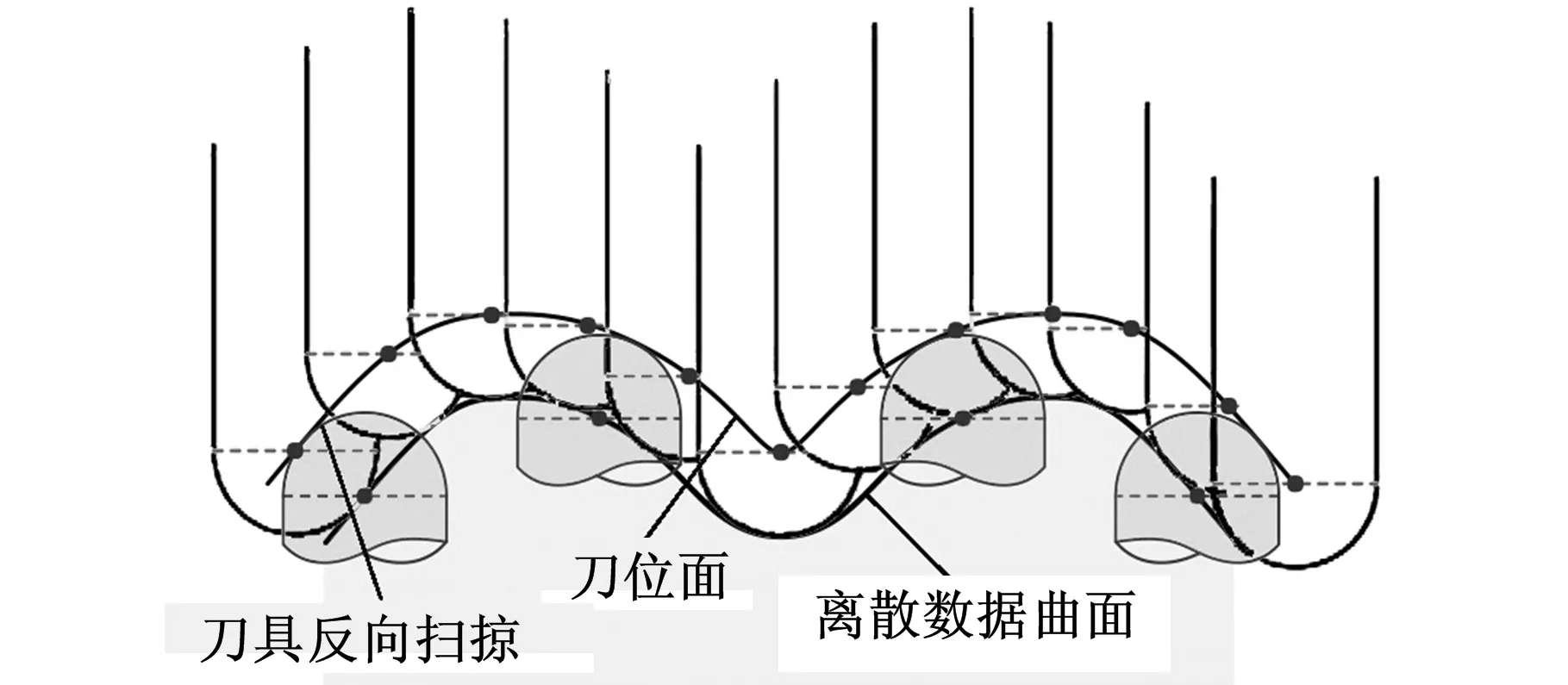
图1 刀位面形成原理
1.2技术路线
受到图像处理中膨胀思想的启发,本文提出以下技术路线:①基于离散数据各顶点产生与加工刀具半径等长的点膨胀球模型;②借鉴计算几何方法中的三维凸包算法,通过一个凸包冗余点滤除器获取点膨胀球模型的最外层包络面数据;③利用MLS投影操作去除可能存在的膨胀奇异点,并通过MLS局部拟合完善去除点和裂缝的拓扑连接,生成无自交的离散数据刀位面网格数据。技术路线如图2所示。
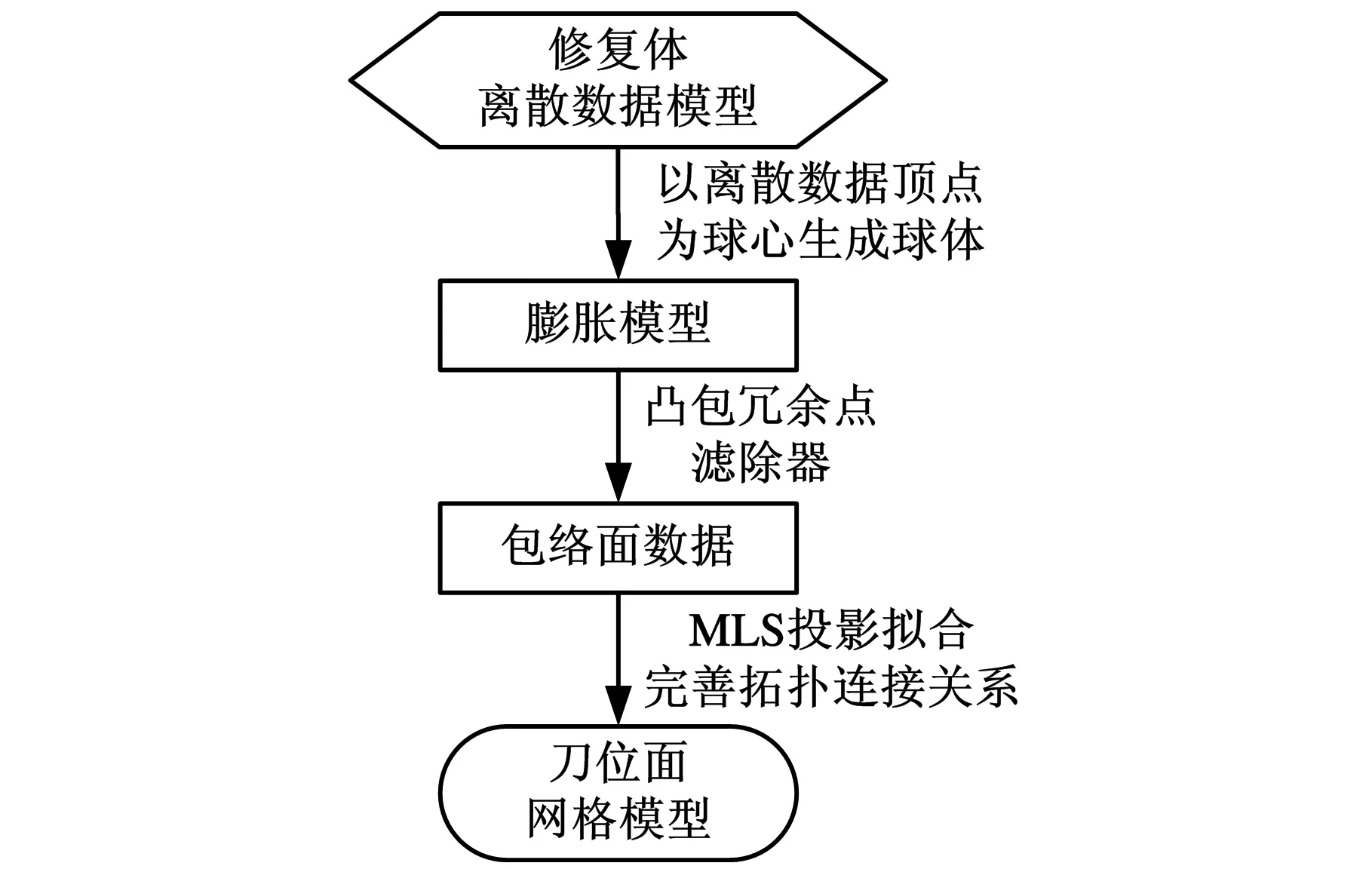
图2 刀位面生成算法技术流程图
2 点膨胀球模型包络面数据的生成
2.1离散数据模型缺陷的分类
经过逆向工程生成的离散数据可能存在裂缝和非二维流形奇异点这2种缺陷。技术人员可以根据缺陷的自身特性对这些缺陷进行具体的定义和分类,并根据缺陷的不同情况设计一个容差的离散数据刀位面生成算法。
2.1.1离散数据裂缝的定义和分类

(a)缝隙示意图

(b)裂纹示意图图3 裂缝的分类
如前言所述,测量获得的离散数据表面由于各种原因,存在部分信息缺失,此时需要定义参数才能对这些缺陷进行定量分析。设定参与加工的球头铣刀刀具半径为R,同时获取缺失信息的最小纵向距离dw和最大横向距离dl。依据参数大小对存在的缺失信息进行分类:①dl≫2R,离散数据表面存在空洞,待加工模型数据存在重大信息缺失,不能正常加工,需要重新采样;②2R>dl,离散数据表面存在缝隙,如图3a所示;③dl>2R>dw,离散数据存在裂纹,如图3b所示。此处把影响离散数据刀位面生成的缺失信息统称为裂缝。2.1.2非二维流形奇异点的定义和分类
在计算机图形应用领域,研究人员定义曲面为一个嵌入于IR3连续定向的二维流形。这种曲面是一个非退化三维实体的光滑边界曲面,能够适当地分离实体的“内部”和“外部”[13]。那些不遵循二维流形定义,存在于曲面内部和外部凸起的异常点和面称为非二维流形奇异点和面。这些缺陷可以依据其空间方向进行定义和分类。其中,与离散数据表面法向量n方向一致的方向为曲面外方向,与表面法向量方向相反的方向为曲面内方向。根据非二维流形奇异点不同的空间位置,可以把非二维流形奇异点分为以下几种类型:①若非二维流形奇异点位于离散数据曲面空间的外部,则定义该非二维流形奇异点为外部奇异点,如图4a所示;②若非二维流形奇异点位于离散数据曲面空间的内部,则定义该非二维流形奇异点为内部奇异点,如图4b所示;③若非二维流形奇异点位于离散数据表面,则定义该非二维流形奇异点为相交奇异点,如图4c所示。
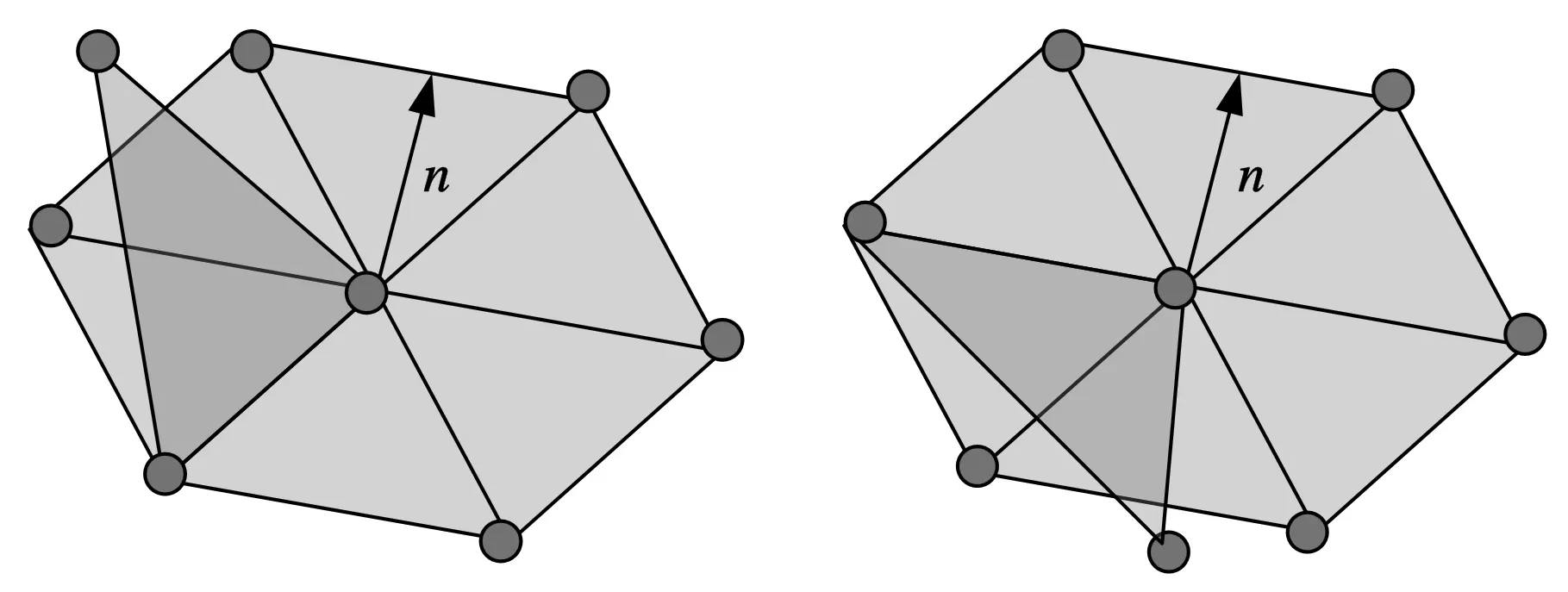
(a)外部奇异点(b)内部奇异点
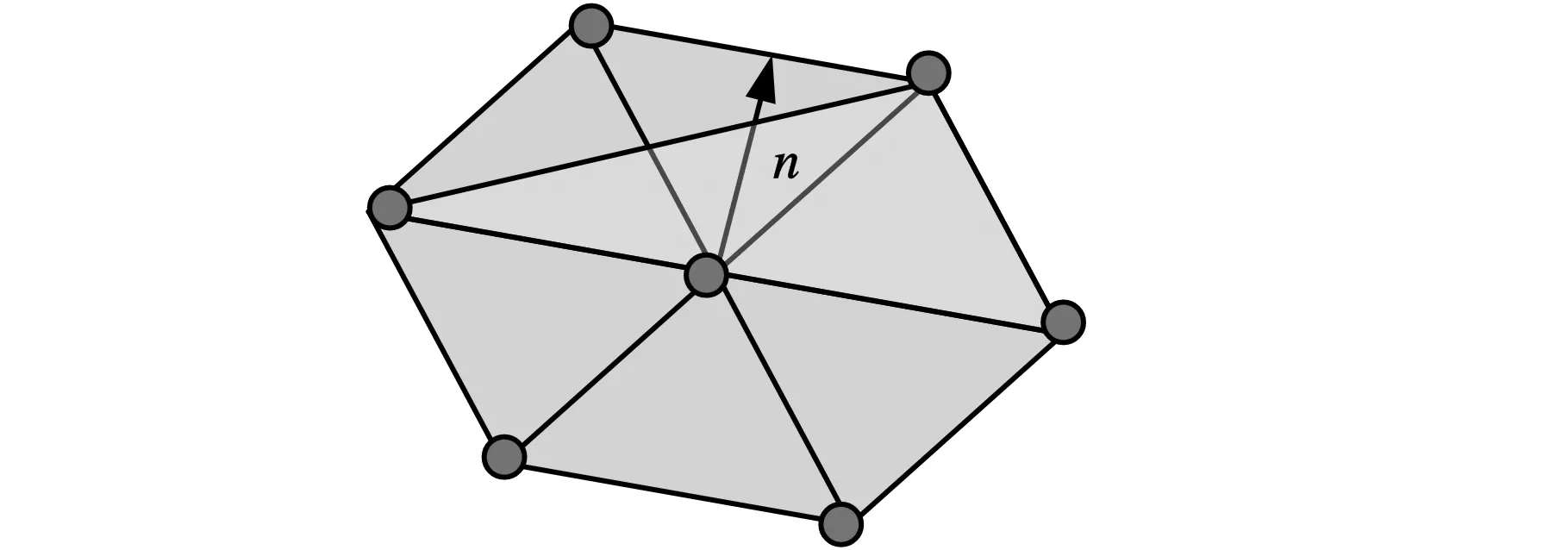
(c)相交奇异点图4 非二维奇异点的分类
2.2离散数据点膨胀球模型的建立
球头铣刀加工离散数据模型时,依据上述刀具反向原理,刀具正向加工刀位点扫掠的曲面和刀具沿着加工曲面反向扫掠得到的曲面重合。此时,球头铣刀可以简略成一个等刀具半径的球体,该球体沿着离散数据曲面滚动所生成的最外层包络面就是刀位面。因此,以离散数据内部各点为球心,生成等球头刀刀具半径的球体。该模型可近似为球头刀动态扫掠生成的扫掠体,从而进一步获取离散数据的球头铣刀刀位面。
离散数据生成点膨胀球模型时,离散数据上的裂缝边缘也会生成相应的膨胀球体。这些膨胀球体组成的包络体和刀具在裂缝上扫掠得到的扫掠体重合。所以,可以利用生成的膨胀球体的最外层包络数据拟合出裂缝处的刀位面数据。离散数据缝隙和裂纹处的点膨胀球模型分别如图5a、图5b所示。
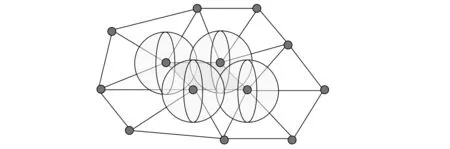
(a)缝隙的膨胀球模型
(b)裂纹的膨胀球模型图5 不同位置的膨胀球模型
同时,通过生成离散数据的点膨胀球模型可以部分消除非二维流型奇异点对离散数据刀位面生成的影响。远离离散数据模型的外部奇异点的膨胀数据如图6a所示。内部奇异点的膨胀球数据存在于离散数据整体点膨胀球模型的内部,如图6b所示。相交奇异点的膨胀球数据位于整个离散数据的点膨胀球模型上,如图6c所示。由于重新规划拓扑连接,对最终生成的刀位面数据没有影响,因此针对一般情况的离散数据,通过构造离散数据的点膨胀球模型可以避免部分缺陷对离散数据刀位面产生的影响。
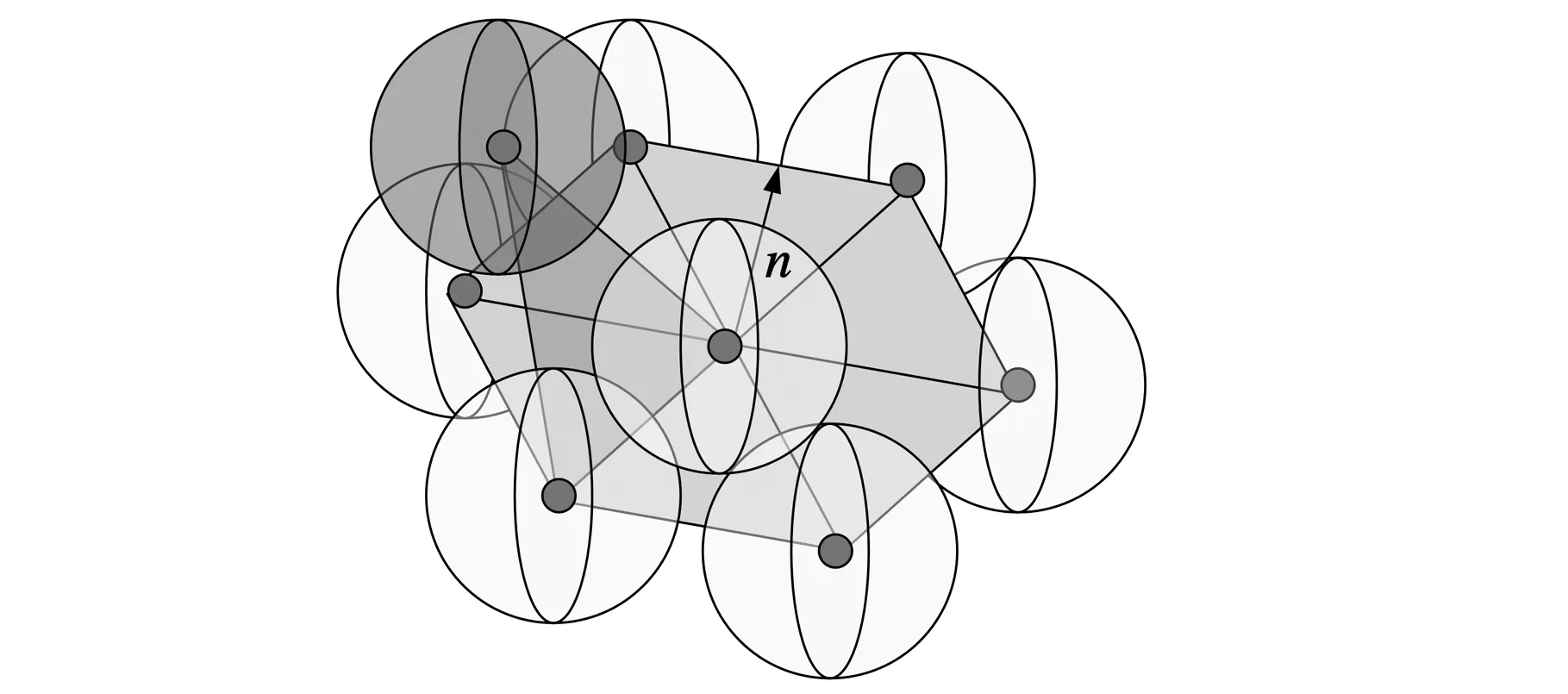
(a)外部奇异点的点膨胀球模型
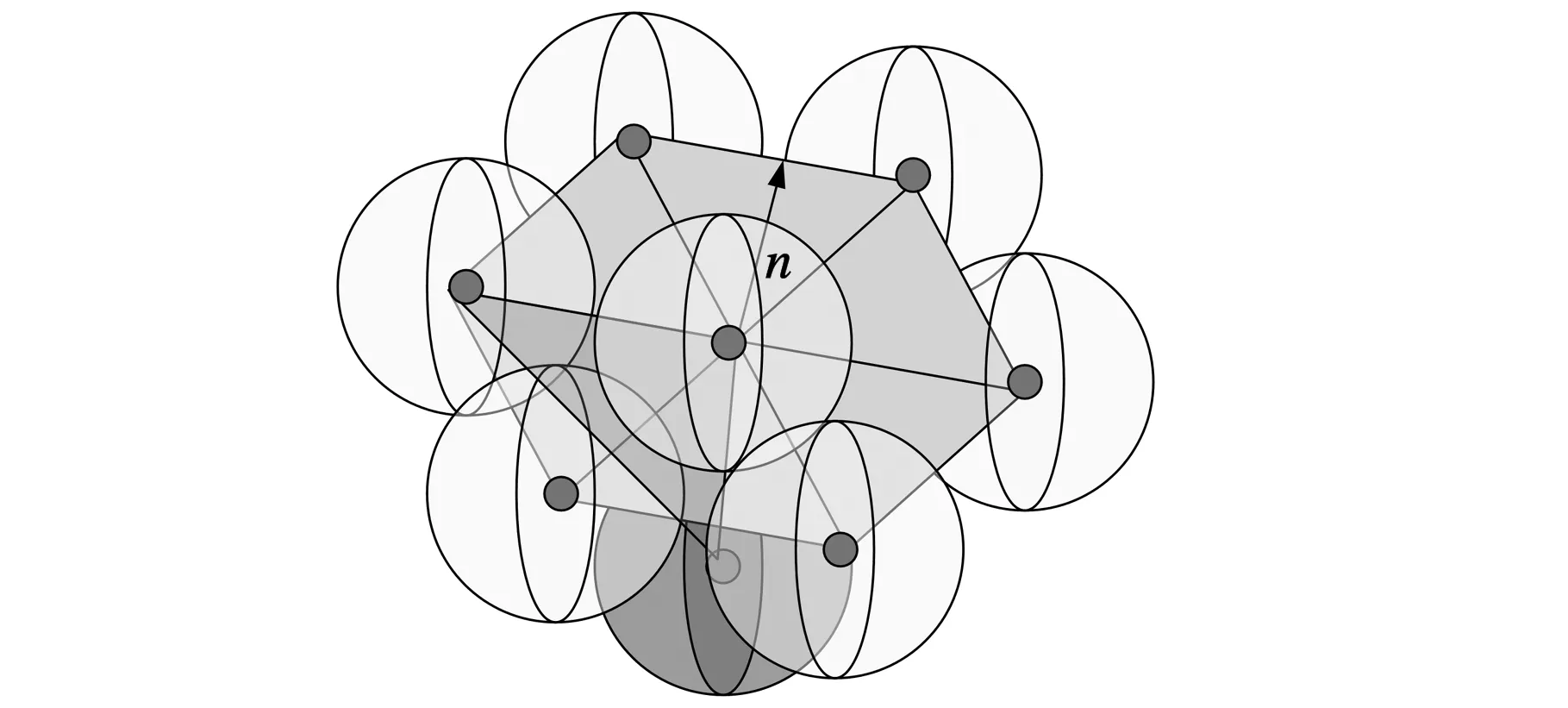
(b)内部奇异点的点膨胀球模型
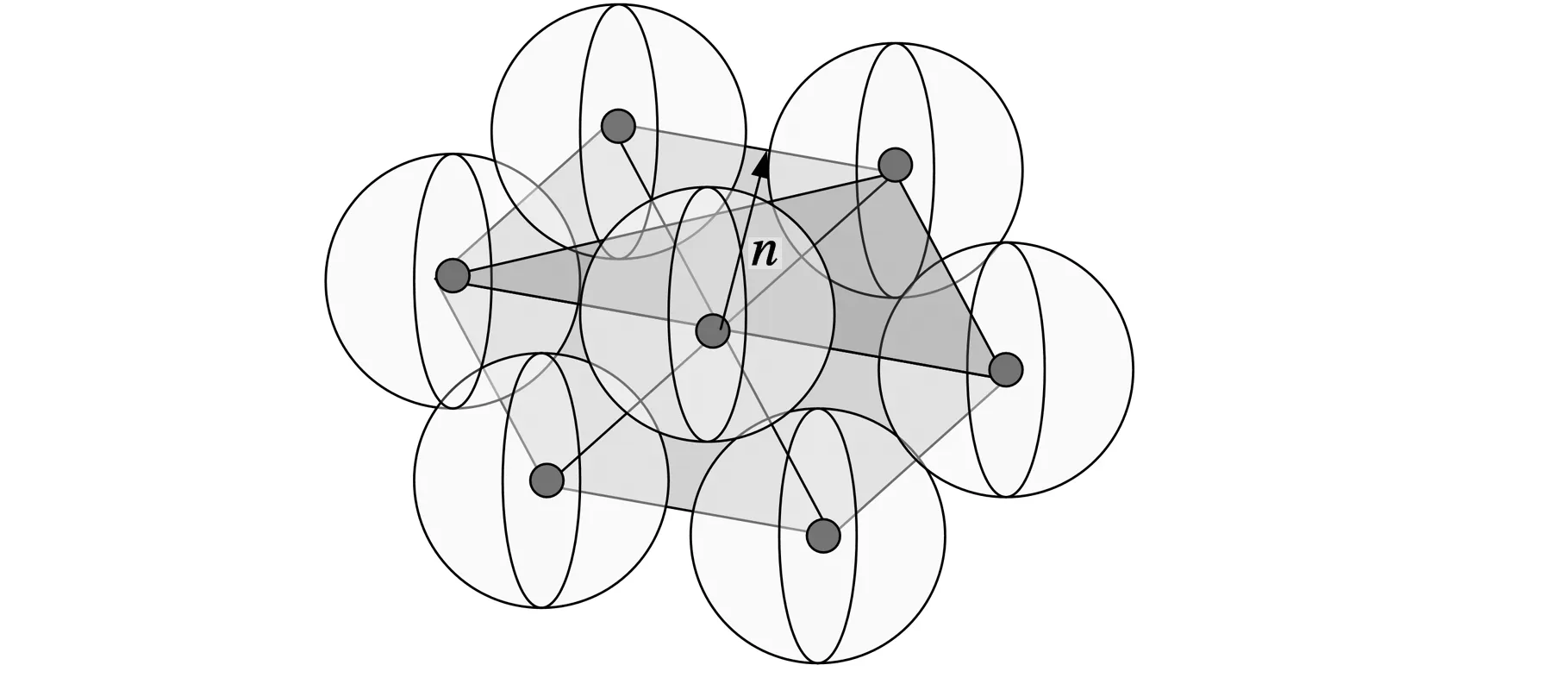
(c)相交奇异点的点膨胀球模型图6 离散数据的点膨胀球模型
一定程度上,膨胀球体的点云数量影响了点膨胀模型外表面的连续性,进而影响了刀位面的生成精度,所以在建立离散数据点膨胀球模型之前需要确定单个球体的点云数量。以下根据离散数据的点云数据量Lm、球模型半径R(mm)、离散数据点与点之间平均长度De(mm)和刀位面的精度级别Uc,设定膨胀系数Qswell来确定单个膨胀球体的点云数量。通过实验分析获得离散数据膨胀系数:
(1)
离散数据膨胀系数和各参数的函数关系如图7所示。通过图7分析可知,随着刀位面精度要求的提高,膨胀系数也会相应增加。工程人员需结合加工模型的实际情况设定参数,确定合理的膨胀系数。
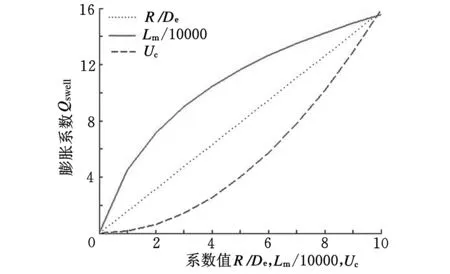
图7 点膨胀球模型的膨胀函数系数图
离散数据点膨胀球模型的建立分为两个过程:(1)对于不同类型的离散数据建立相同的数据结构进行存储。其中,分别采用KD树和半边结构分别建立点云数据和网格数据间的邻域关系。(2)数据存储完后,遍历离散数据点集链表Vlist,以每个顶点数据为球心,一环邻域为边界,根据膨胀系数Qswell生成当前顶点的部分球体。该球体的半径等于球头铣刀的刀具半径,且由一系列点云表示。
2.3点膨胀球模型包络数据的建立
球头铣刀离散数据加工刀位面和等球头刀具半径的点膨胀球模型最外层包络曲面重合,通过获取离散数据点膨胀球模型最外层的包络数据,可生成离散数据的刀位面[14]。离散数据模型存在局部曲面曲率小于球头刀刀具半径的区域,所以该区域的点集以及内部奇异点生成的膨胀球体存在于离散数据点膨胀球模型的内部[15]。运用凸包算法可以直接获取离散数据点膨胀球模型的外层包络面,这样就可以避免判断自交和去除自交的复杂过程,从而获取最终的包络面数据[16]。所以,基于凸包原理设计的凸包冗余点滤除器可以快速获得点膨胀球模型的最外层包络面数据。
凸包冗余点滤除器的具体实施过程:采用KD树快速确定点云内部的邻域关系,遍历离散数据点集Vlist,通过计算两点Vi、Pa的欧氏距离d(Vi,Pa)判断、删除存在于整个点膨胀球模型内部的膨胀球数据。然后,通过凸包原理依次获取每个外部膨胀球模型的最外层顶点,并且把它作为外部包络数据点存入包络点集Vconvex。以下为冗余点滤除器的部分伪代码。
Step 1:
If(所有点指针访问标志isvisited为真){转Step 3;}
Else{依次遍历离散数据模型点链表Vlist中点的指针,使其成为当前结点Vi;转Step 2;}
Step 2:
While((Vi)isvisited=false){(Vi)isvisited=true;
for(遍历离散数据点膨胀球模型n维领域点集Pswell) {d=distance(Vi,Pa);
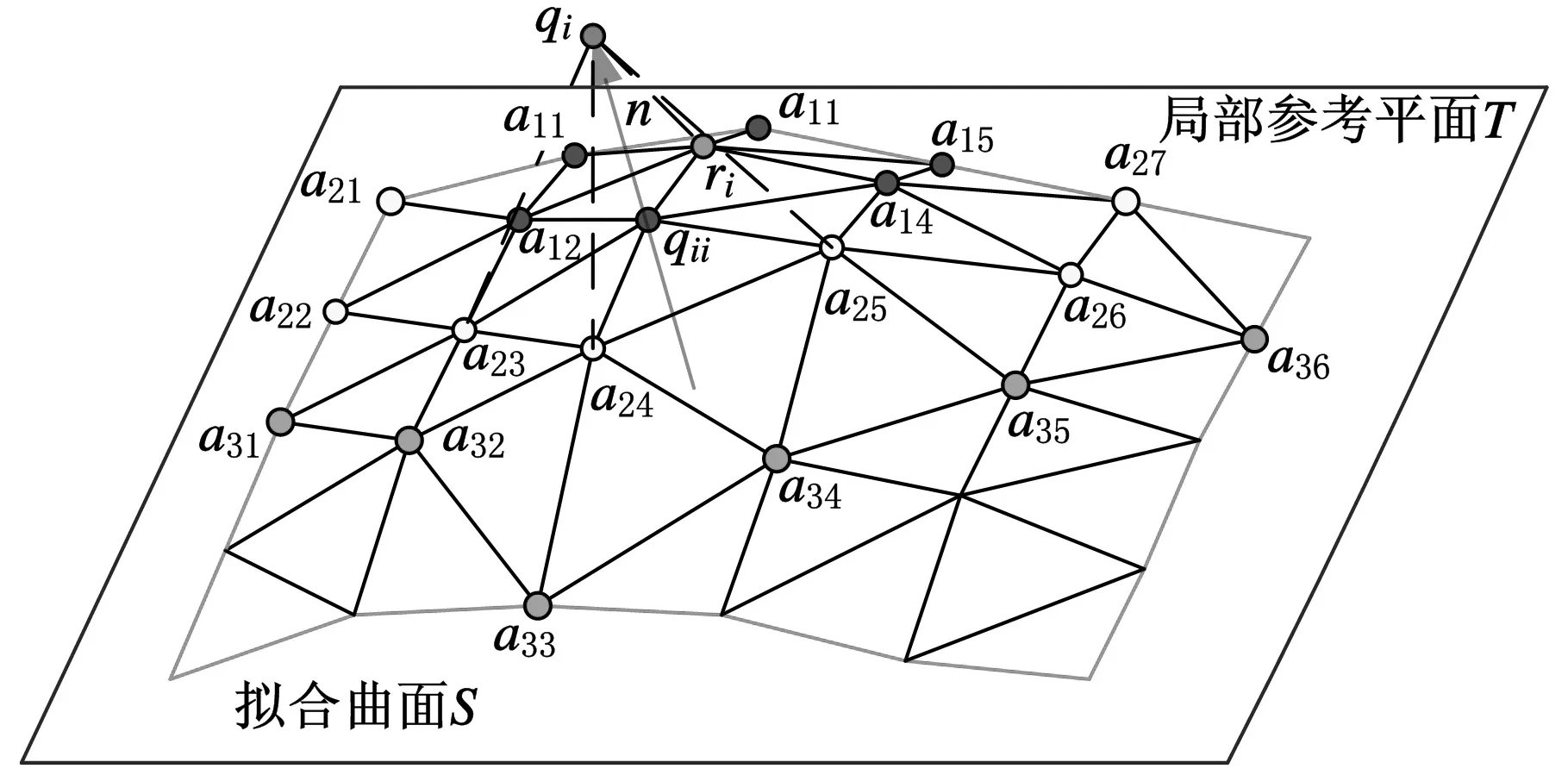
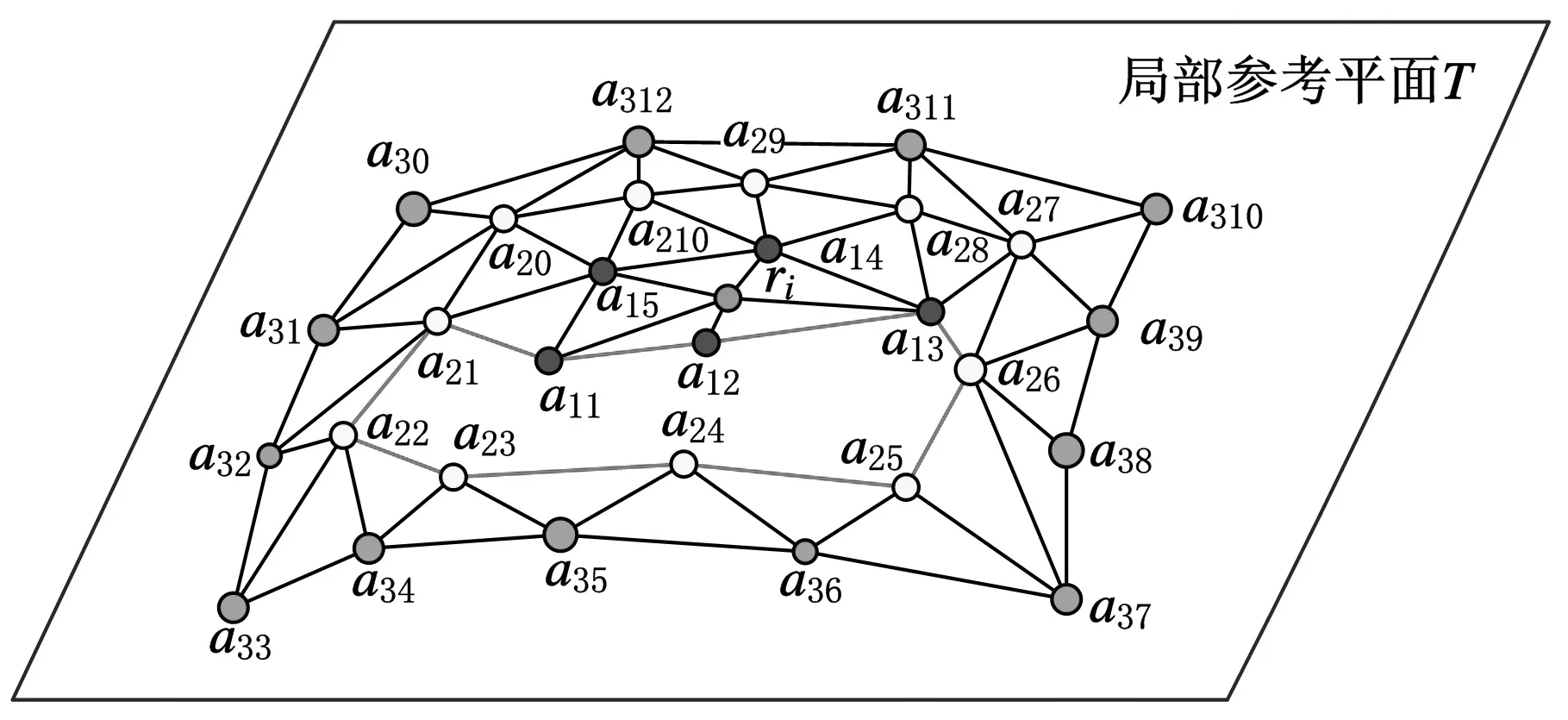
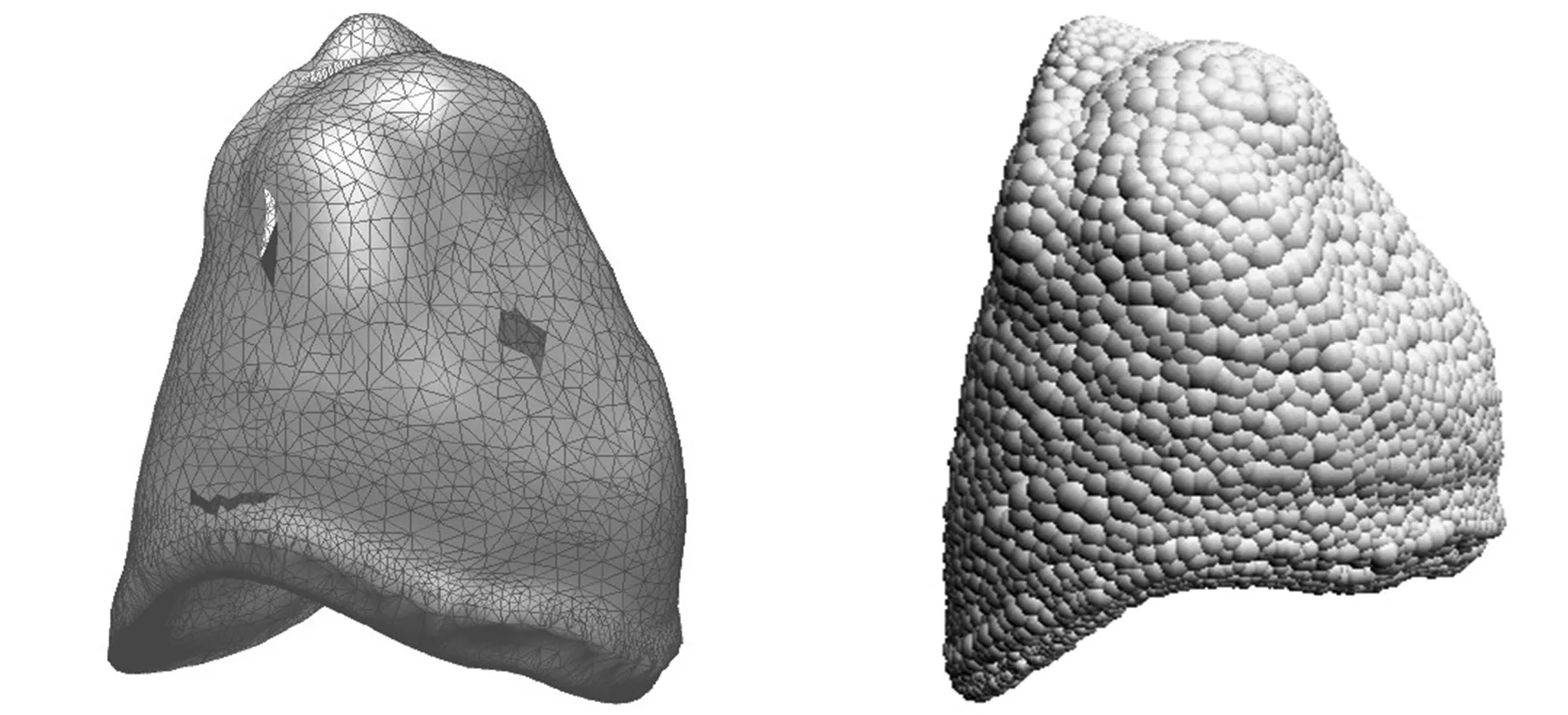
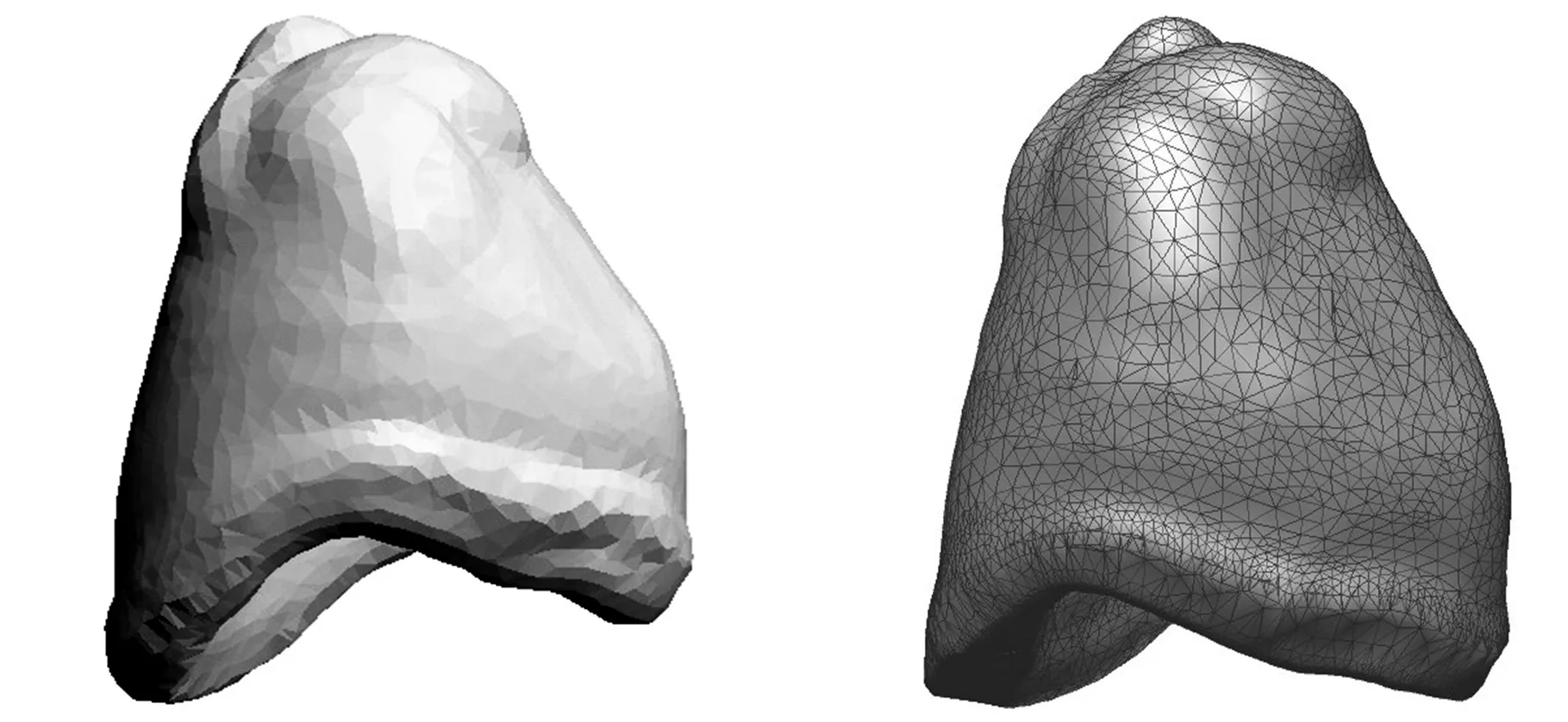
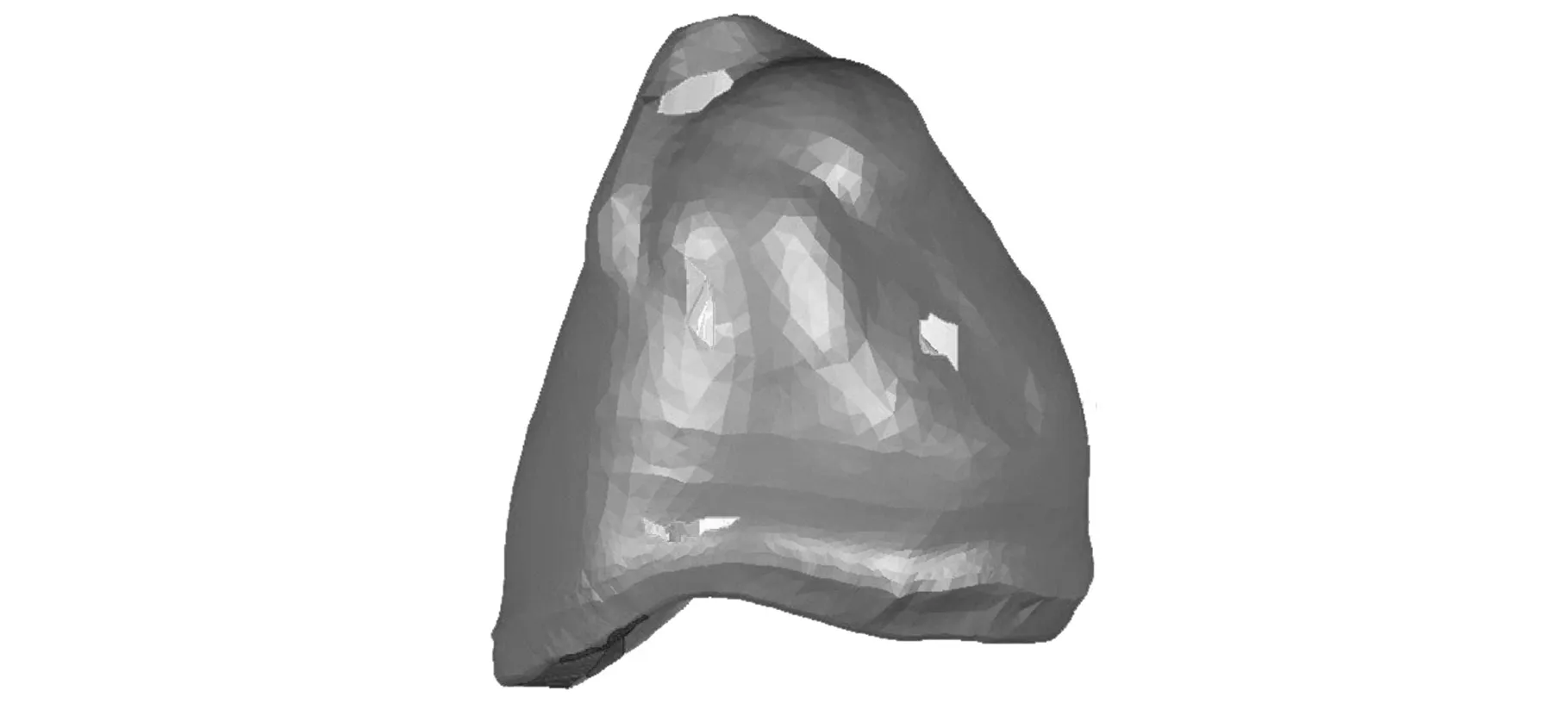
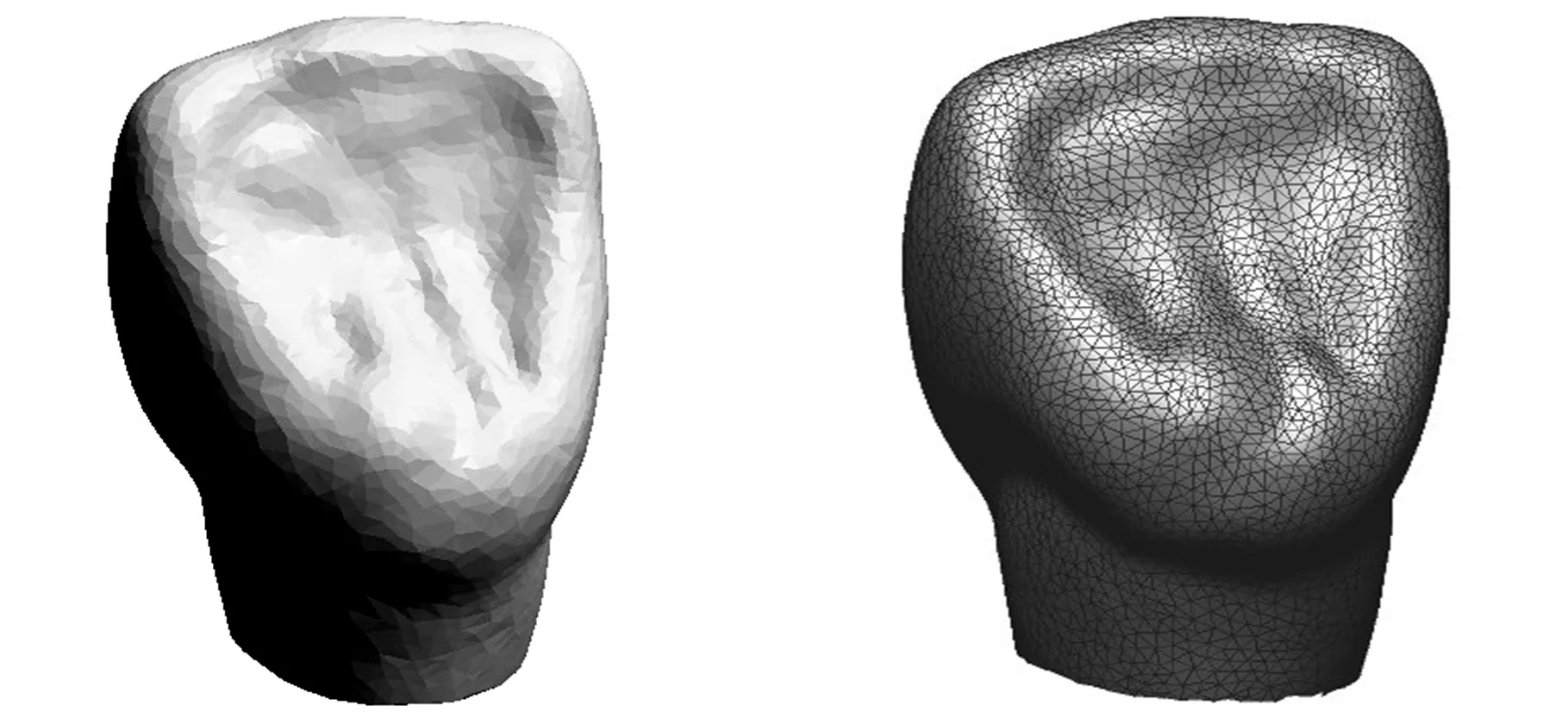
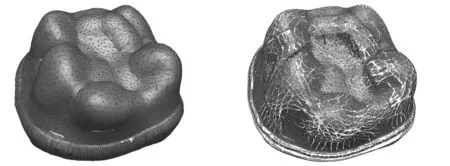
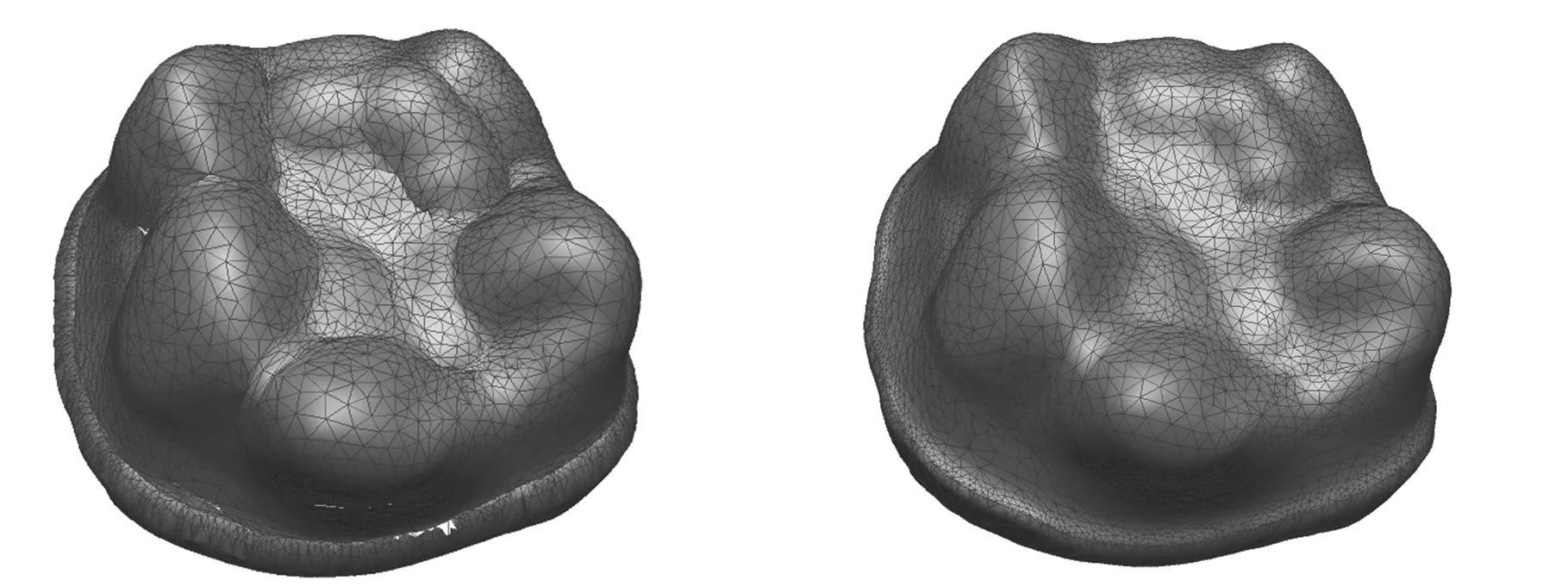
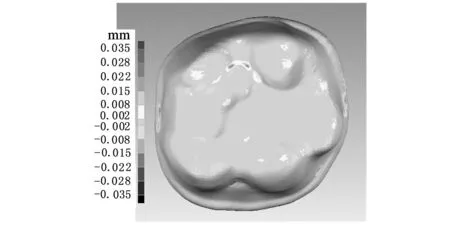
If (d Else{Viis_swell=convhull(Pi); If (Viis_swell==1); Vconvex=Pi;将最外层点Pi插入凸包点集Vconvex;}}}转Step 1; Step 3: 最外层包络数据建立完成。 经过上述凸包冗余点滤除器处理后的离散数据点膨胀球模型外部的包络数据可能会存在局部误差,如图8a所示。误差derror与刀具半径和离散数据点之间的间距d有关,且误差大小范围为0≤derror (a)局部误差示意图 (b)获取外部包络数据建立凸包示意图图8 点膨胀球模型包络面建立示意图 离散数据可能存在外部奇异点和裂缝,需要对获取的外部包络数据进行局部曲面拟合。通过采样局部拟合后的曲面添补刀位面缺失的真实信息,最终获得曲面特性较好的刀位面网格数据。MLS拟合是一种离散数据快速拟合方法。通过该拟合方法获得的曲面叫做MLS曲面。研究表明,MLS曲面拟合方法具有拟合精度高、模型表达简单等特点,同时可减小噪声点带来的误差[17]。相对于传统简单的拟合数据,离散数据的数据存储量大、空间分布不均匀,所以针对数据量较大的离散数据可采用MLS投影拟合的方法获得离散数据的局部MLS曲面[14]。因此,本文采用这种局部曲面拟合的方法消除外部奇异点对刀位面的影响,同时添加可能存在的缺失信息,生成表面质量较高的刀位面网格数据。此处的MLS投影拟合过程分为两个步骤:①建立局部参考平面,通过设定阈值,完成MLS投影,去除并标记可能存在的外部奇异点;②对拟合点参数化,并完成局部多项式曲面拟合,移动拟合区域生成全局刀位面数据。 3.1MLS投影去除外部奇异点 离散数据表面可能存在外部奇异点,经过上述处理后,外部奇异点产生的膨胀点存在于离散数据点膨胀球模型的外部包络面上。本文通过设定阈值,实现MLS投影,从而删除这些外部奇异点产生的奇异膨胀点。首先,获取离散数据点膨胀球模型的外部包络点集Vconvex中点rj的一环邻域面。依据环领域面的面积加权平均各面法矢估算点rj的近似法向量n。设定与该法向量空间正交的平面T为点rj的局部参考平面。该图局部参考平面T的数学表达式为 T={rn|(n,ri-rj)=0,rn∈R3} (3) n∈R3并且|n|=1 式中,(n,ri-rj)表示向量n与向量ri-rj的叉乘积。 图9 MLS投影判断、去除奇异点qi 为了更有效去除奇异膨胀点,同时保证投影在局部参考平面T上的点满足下式: (4) 其中,|n,ri|为顶点ri在rj法向量方向上的投影距离hj;l为在rj法向量方向上的投影距离;w为高斯权函数[18],w=exp(-d2/k2);参数k是rj的一环领域边长的平均值;变量d为ri、rj两点之间的欧氏距离|ri-rj|。高斯权函数w(qi-rj)=exp(-|qi-rj|2/k2)具有指数变化的特性,权重w(qi-rj)会随着偏离距离|qi-rj|的增加指数级地减小。所以高斯权函数降低了膨胀偏离点qi对局部拟合曲面S的影响,从而使曲面更加的光顺。 3.2刀位面网格数据的生成 离散数据的点膨胀球模型的包络数据保持着一定的网格连接关系。离散数据的网格连接关系会随着删除奇异膨胀点的操作发生相应改变。对删除点的区域进行局部拟合,获取奇异膨胀点处真实的曲面信息可以有效解决这一问题。设当前删除点为qi,那么qi的三阶领域环所在空间范围就是局部曲面拟合区域。在局部参考平面T内,对点集{ri}内的点的坐标参数化,并建立拟合曲面的目标函数S(u,v): S(u,v)=Au2+Buv+Cv2+Du+Ev+F (5) 式中,A、B、C、D、E、F为该拟合曲面的系数[19]。 同时建立局部拟合误差范式: (6) 使其在当前拟合条件达到最小[17]。其中,p(xi)为二次函数的基[u2v2uvuv1]T;a(xi)为待求曲面S(u,v)的系数;fi为点ri所对应的真实值。 图10 MLS拟合获取奇异点qi真实点 如图11a所示,当曲面存在裂缝时进行局部曲面拟合,通过判断包络点间距,可以有效地拟合裂缝处的曲面信息如图11b所示。从而生成网格曲面分布均匀、质量较好的离散数据刀位面的网格数据。 (a)存在裂缝的局部曲面 (b)MLS拟合获取裂缝缺失信息图11 存在外部奇异点刀位面生成过程 基于MLS拟合带容差的离散数据加工刀位面生成算法已在PC上的VC2008和MATLAB软件开发平台中实现应用,应用本文提出的技术路线生成离散数据刀位面和用商业软件的偏距功能生成相同模型的刀位面实例如图12、图13所示。 (a)存在裂缝的点云数据(b)点膨胀球模型 (c)点膨胀球模型凸包包络面(d)刀位面三角网格模型 (e)商业软件生成的刀位面数据图12 存在裂缝的尖牙刀位面的生成过程 (a)存在奇异点的网格模型(b)点膨胀球模型 (c)点膨胀球模型凸包包络面(d)刀位面三角网格模型 (e)商业软件产生的刀位面数据图13 存在奇异点的切牙刀位面的生成过程 图12所示为存在裂缝的修复体尖牙点云数据刀位面生成过程:图12a所示为存在裂缝的修复体尖牙点云数据,首先生成的尖牙的点膨胀球模型如图12b所示,然后根据凸包原理生成的点膨胀球模型包络面如图12c所示,最终经过以上处理生成的刀位面见图12d,本文用商业软件里的偏距功能生成相同模型的刀位面数据如图12e所示。图13所示为存在非二维流形奇异点的修复体切牙网格模型刀位面生成过程:图13a所示为存在非二维流形奇异点的修复体切牙网格模型,该切牙的点膨胀球模型如图13b所示,该切牙的点膨胀球模型的凸包包络面如图13c所示,经过本文算法处理生成的最终切牙刀位面模型见图13d,用商业软件产生的刀位面数据则如图13e所示。 实际工程应用中,技术人员根据加工阶段和加工模型的大小选用不同刀具半径的球头刀。因此,球头刀刀位面的生成算法应满足不同尺寸的生成要求。本算法以磨牙为例,生成不同刀具半径的加工刀位面,如图14、图15所示。同时,应用其他基于偏距原理的刀位面生成算法生成加工刀具半径为0.5 mm的磨牙模型的刀位面,利用商业软件对生成结果依次进行了实验对比,误差分析对比见图16,各参数如表1所示。通过上述实例分析,本算法生成的刀位面网格质量较高,生成过程较稳定;当生成较大半径的球头铣刀刀位面时,刀位面内部不存在自交。 (a)点向量法(b)面向量法 (c)多重向量法(d)本文算法图14 各种算法生成的球头刀磨牙加工刀位面 (a)点向量法 (b)面向量法 (c)多重向量法 (d)本文算法图15 各种算法生成的球头刀磨牙加工刀位面实验结果 (c)Doffset=1.0 mm(d)Doffset=1.5 mm图16 本算法生成的不同Doffset的刀位面 基于偏距原理生成刀位面的方法评价参数自交平均误差(μm)裂缝奇异点算法时间复杂度点数、面数点向量法有8有有O(n):[2.535s]相同面向量法有9有有O(n)+bO(n):[4.375s]急剧增加多重向量法有6有有O(n)+bO(s):[6.790s]增加本算法无4无无O(n)+bO(e):[5.105s]基本相同 注:磨牙网格文件由13 071个点、26 138个面组成,其中,n为离散数据的面数,b为后续操作的时间复杂度的复合系数,bO(n)为去除自交的时间复杂度,s为待去除的尖状点和边的总数(s≪n),e为奇异点和裂缝的总数。 (1)本文首先对离散数据一般存在的缺陷进行了定义和分类,然后将计算几何凸包原理和MLS局部曲面拟合技术应用到离散数据刀位面的生成研究上,实现了存在缺陷的离散数据刀位面的生成算法。针对存在缺陷的离散数据,首先生成与球头铣刀刀具半径等距的点膨胀球模型;然后,应用凸包冗余点滤除器获取点膨胀球模型 的最外层包络面;最后,采用MLS局部投影拟合的方法去除存在的外部奇异膨胀点,并修复由外部奇异膨胀点的删除和裂缝所导致的包络数据网格的缺失,从而得到最终的刀位面网格模型。 (2)切牙等离散数据刀位面的生成实例表明,所提出的算法能够解决存在空裂缝和非二维流形奇异点的离散数据刀位面生成问题。在生成刀位面的过程中,省去了修补、删除等离散数据预处理操作,同时避免了刀位面内部自交问题,为后续数控加工节省了时间,提高了效率。 (3)本文提出的技术路线尚有不足之处。因为本算法通过点膨胀球模型获得的是等距的球头铣刀刀位面,所以不适用于实现不等值偏距的其他APT刀具刀位面的生成,这需要在后续研究中进一步完善。因此,为了适用于更广阔的加工领域,研究广义APT刀具的刀位面生成算法将是未来的一个重要研究点。 [1]Lasemi A,Xue Deyi,Gu Peihua.Recent Development in CNC Machining of Freeform Surfaces:A State-of-the-art Review[J].Computer-Aided Design,2010,42(1):641-654. [2]Lin A C,Liu H T.Automatic Generation of NC Cutter Path from Massive Data Points[J].Computer-Aided Design,1998,30(1):77-90. [3]董光雷.面向齿科数控加工轨迹的高效生成方法研究[D].南京:南京航空航天大学,2011. [4]Choi B K,Jerard R B.Sculptured Surface Machining[M].Dordrecht:Kluwer,1999. [5]Choi B K.Surface Modeling for CAD/CAM[M].Amsterdam:Elsevier,1991. [6]Jun C S,Kim D S,Park S H.A New Curve-based Approach to Polyhedral Machining[J].Computer-Aided Design,2002,34(5):379-389. [7]Ren Yongfu.Computational Techniques to Improve Efficiency and Accuracy for High Performance Machining of Polyhedral Models[D].Raleigh:North Carolina State University,2002. [8]Kim Su-Jin,Yang Min-Yang.Triangular Mesh Offset for Generalized Cutter[J].Computer-Aided Design,2005,37(5):999-1014. [9]赵巍,戴宁.基于特征点的离散建模偏置技术研究[J].中国制造业信息化:学术版,2012,41(9):38-42. Zhao Wei, Dai Ning. Study of Discrete Modeling Offset Technology Based on Feature Pionts [J].Manufacture Information Engineering of China,2012,41(9):38-42. [10]Chen Yong,Wang C L.Uniform Offsetting of Polygonal Model Based on Layered Depth-normal Images[J].Computer-Aided Design,2011,43(1):31-46. [11]Park S C,Chung Y C.Tool-path Generation from Measured Data[J].Computer-Aided Design,2003,35(5):467-475. [12]Park S C.Sculptured Surface Machining Using Triangular Mesh Slicing[J].Computer-Aided Design,2004,36(3):279-288. [13]Botsch M,Pauly M,Kobbetl L,et al.Geometric Modeling Based on Polygonal Meshes[J].ACM Siggrapd,2007,36(5):221-234. [14]Kim Soo-Kyun,Kim Chang-Hun.Finding Ridges and Valleys in a Discrete Surface Using a Modified MLS Approximation[J].Computer-Aided Design,2005,37(7):1533-1542. [15]Fasshauer G E. Toward Approximate Moving Least Squares Approximation with Irregularly Spaced Centers[J].Computer Methods in Applied Mechanics and Engineering,2004,193(1):1231-1243. [16]杨文玉,胡雯蔷,熊有伦.基于三维凸包的可变形离散网格模型[J].中国机械工程,2004,15(22):2040-2043. Yang Wenyu,Hu Wenqiang,Xiong Youlun.A Deformable Mesh Model Based on Convex Hull of Scattered Points[J].China Mechanical Engineering,2004,15(22):2040-2043. [17]曾清红,卢德堂.基于移动最小二乘法的曲线曲面拟合[J].工程图学学报,2004,25(1):84-89. Zeng Qinghong,Lu Detang.Curve and Surface Fitting Based on Moving Least-squares Methods[J].Journal of Engineering Graphics,2004,25(1):84-89. [18]刘福保,李卫国.散乱数据曲面拟合的局部加权最小二乘插值方法及权函数的选择讨论[J].数学理论与应用,2009,29(1):113-117. Liu Fubao,Li Weiguo.The Topic on Choice of Weighted Functional and Local Weighted Leased-mean Square Method for Surface Interpolation to Scattered Data[J].Mathematical Theory and Application,2009,29(1):113-117. [19]钱归平.散乱点云网格重建及修补研究[D].杭州:浙江大学,2008. (编辑张洋) An Algorithm for Tolerance Cutter-location Surface Generation of Measured Data Based on MLS Method Li Xiangjia1Dai Ning1Liao Wenhe1Guo Baosu1Wang Yongbo2 1.Nanjing University of Aeronautics and Astronautics,Nanjing,210016 2.Shinva Medical Instrument Co., Ltd.,Zibo,Shandong,255086 Traditional offset method can not directly generate the cutter-location surface of measured data with defects.Thus,a tolerance method of cutter-location surface generation was proposed based on MLS fitness.Firstly,the measured data were transformed to a swelling ball model by the length of ball-end cutter’s radius. Secondly,according to the geometric principle of convex hull,outer envelope data of this swelling ball model were acquired.Finally,local MLS projection fitting method was used to eliminate possible defects,and generated the final cutter location mesh surface.It is shown that this algorithm is able to generate cutter-location surface of measured data even they have defects,and also is suitable for the practical engineering applications for its high efficiency and accuracy. moving least squares(MLS);tolerance;measured data;NC machining;cutter-location surface 2013-06-13 国家科技支撑计划资助项目(2012BAI07B04);国家自然科学基金资助项目(51205192,81271181);国家高技术研究发展计划(863计划)资助项目(SS2013AA040801-02);南航科研基地创新基金资助项目(NJ20130015) TP391DOI:10.3969/j.issn.1004-132X.2015.08.010 李向佳,女,1989年生。南京航空航天大学机电学院硕士研究生。主要研究方向为数字化设计与制造、生物医学工程。戴宁,男,1978年生。南京航空航天大学机电学院副教授。廖文和,男,1965年生。南京航空航天大学机电学院教授、博士研究生导师。郭保苏,男,1986年生。南京航空航天大学机电学院博士研究生。王永波,男,1979年生。山东新华医疗器械股份有限公司工程师。

3 离散数据刀位面的生成
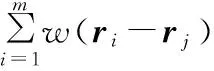


4 实验与分析






5 结论

