三自由度等刚度永磁弹簧的力学特性研究
孙 凤 张 明 孙兴伟 金俊杰 李 清 李殿起 王 可
沈阳工业大学,沈阳,110870
三自由度等刚度永磁弹簧的力学特性研究
孙凤张明孙兴伟金俊杰李清李殿起王可
沈阳工业大学,沈阳,110870
设计出一种三自由度等刚度永磁弹簧,并根据单组永磁体结构,采用虚位移法建立其径向磁力解析模型,利用有限元方法对径向磁力进行了仿真计算。仿真结果和模型计算结果基本吻合。解析计算与仿真结果表明,该永磁弹簧的径向磁力随着径向位移的增加而增大,随着轴向位移的增大而减小。在永磁弹簧平动平面内,两个移动方向的刚度系数和垂直于平面中心的回转刚度系数均相等。在径向位移较小时,径向位移与弹簧刚度系数近似成线性关系。
等刚度;永磁弹簧;径向磁力;有限元法
0 引言
金属弹簧在机械行业广泛应用,但它存在产生振动和噪声的缺点。利用永磁体间磁力相互作用的永磁弹簧,具有无机械接触、无磨损、功耗低、寿命长、噪声小等优点,可以取代金属弹簧用于快速机械响应机构,特别适合于真空、高速和超洁净等特殊的应用场合[1-4]。
高海波等[5]将磁弹簧减------------------------
震器(没有严格的密封要求)应用于行星轮式月球车的减震系统,很好地适应了高度真空的月球表面环境,克服了现有以液体或气体为工作介质的减震器的工作局限性。
文献[3-4]采用有限元法对稀土永磁弹簧的磁场分布进行了数值模拟分析,并就弹簧永磁体的结构参数对弹簧特性的影响作了详细的研究,得出弹簧的力学特性与永磁体的形状和尺寸的关系。文献[6-7]分析了轴向混合磁轴承磁路以及各部分磁导,结合稀土永磁体的工作特性,用虚位移法得出了轴向混合磁轴承的径向承载力解析数学模型。文献[8-10]分析了双磁环和多磁环磁轴承气隙磁导及磁通,得出了磁环间径向磁力解析数学模型。
本文在分析了环形永磁体和柱形永磁体及气隙磁导的基础上,提出了一种径向为工作方向的三自由度等刚度磁弹簧。根据磁弹簧的结构,结合环形永磁体和柱形永磁体的工作特性,用虚位移法建立三自由度等刚度磁弹簧径向磁力解析数学模型,计算径向磁力,分析了径向磁力与轴向位移和径向位移的关系,计算弹簧刚度系数,分析刚度系数和轴向位移的关系,并通过有限元方法对解析计算结果进行验证。
1 结构及工作原理
笔者设计了图1a所示的三自由度等刚度磁弹簧装置。该装置由上顶盖、下底盖、3个环形永磁体、3个柱形永磁体和3个平面球轴承组成。1个环形永磁体和1个柱形永磁体为一组,同轴布置,且相同磁级相对。3组永磁体与3个平面球轴承相互间隔、均匀布置在以装置轴线为中心的同心圆上。将平面球轴承去掉一侧轴承端盖,安装于下底盖,使轴承钢球直接与上顶盖接触,支撑上下两端盖,形成永磁弹簧间轴向的均匀气隙。该弹簧达到稳定支撑和三自由度等刚度的最小组数为3。
如图1b所示,每组永磁体的柱形永磁体和环形永磁体在竖直方向上表现为吸引力,在水平方向上表现为斥力(上顶盖在轴向方向上不会发生窜动)。此种布置的永磁弹簧,在平动平面内,可以沿着x方向、y方向移动和绕c轴转动。结构中,环形永磁体的内半径大于柱形永磁体半径,柱形永磁体从与环形永磁体同轴位置沿平面内任意方向向环形永磁体靠近时,在变化量相等的情况下,两者之间沿平面内任意方向上产生的斥力均相等。因此,在图1a所示由3组永磁体组成的永磁弹簧结构中,沿弹簧的x方向、y方向移动和绕c轴转动时,柱形永磁体和环形永磁体的相对气隙变化量相等时受到的回复斥力相等,即沿x方向、y方向移动和绕c轴的回转的刚度系数数值相等。该永磁弹簧的总回复力为n倍的单组永磁体斥力,总转矩为n倍的单组永磁体回复斥力与单组永磁体中轴线和磁弹簧中轴线间距离之积。永磁弹簧的回复力随着x方向、y方向和c向的位移量增大而增大。最大位移量为环形永磁体的内半径与柱形永磁体半径的差。
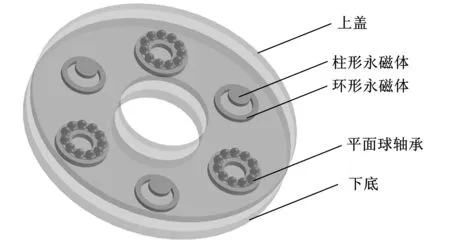
(a)三维结构图
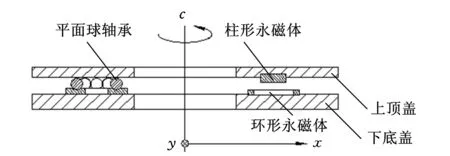
(b)剖视结构图图1 三自由度等刚度磁弹簧结构
2 数学模型
为了对该永磁弹簧各方面的特性进行深入分析。首先建立该系统的数学模型。由于该系统由3组结构完全相同的柱状永磁体和环形永磁体构成。故先建立一组永磁体的模型,如图2所示。
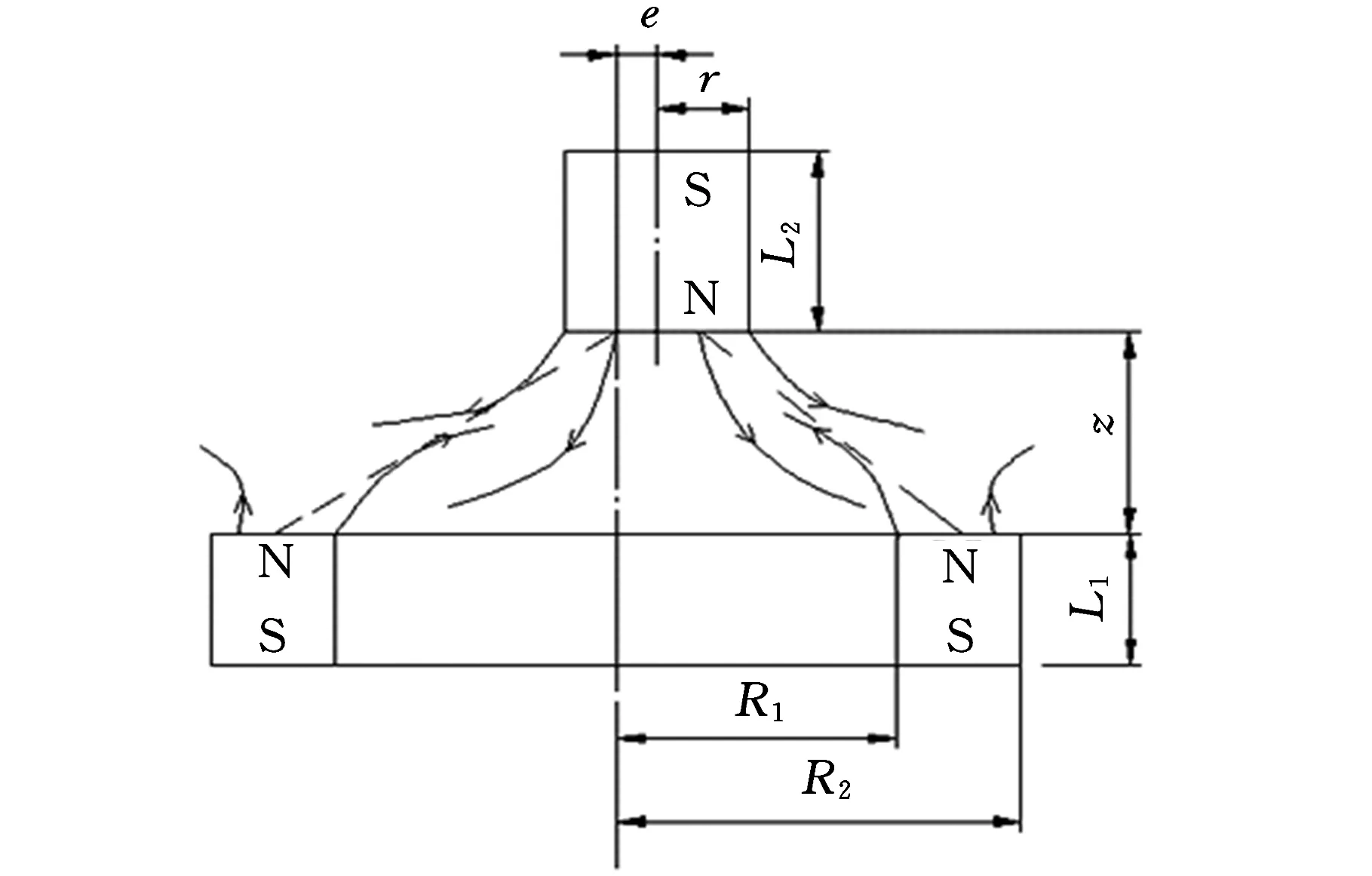
图2 一组永磁体的结构参数
2.1磁导计算
参照半径为r、极间距为z的异性圆柱磁极之间的磁导公式:
G=μ0(πr2/z+1.632r)
(1)
当柱形永磁体和环形永磁体径向位移为e,轴向距离为z时,中轴线右侧磁力线长度gR和中轴线左侧磁力线长度gL可以表示为
(2)
(3)
式中,R2、R1、L1分别为环形永磁体的外径、内径和厚度;r、L2分别为柱形永磁体的半径和厚度。
环形磁极气隙磁导Gg1和柱形磁极气隙磁导Gg2为
(4)
Gg2=μ0(πr2/g+1.632r)
(5)
可得环形磁极与柱形磁极气隙磁导Gg:
Gg=αGg1+βGg2
(6)
根据磁导定义式G=μS/L,得到环形永磁体和柱形永磁体的磁导:
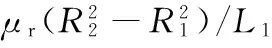
(7)
G2=πμrr2/L2
(8)
式中,μr为钕铁硼永磁材料磁导率。
根据折算到磁极两端的圆柱形永磁铁漏磁导公式可认为,环形永磁铁的漏磁导等于半径为R2的圆柱形永磁体漏磁导与半径为R1圆柱形永磁体漏磁导的和,永磁柱漏磁导等于半径为r的圆柱磁体漏磁导,故有
(9)
GL2≈πμrr2/L2
(10)
半径为r,间距为z,厚度为L的两圆柱体侧面磁导公式为
Gc=2μ0Lr/(1+g)
式中,g为磁力线长度。
因此环形永磁体内外两个侧面磁导Gc1和Gc2为
(11)
(12)
(13)
式中,Ga为磁路总磁导。
将式(6)~式(12)代入式(13)可得:
(14)
将式(2)、式(3)代入式(14)得到中轴线右侧总磁导GaR和中轴线左侧总磁导GaL。
根据式(2)、式(3)和式(6)得到气隙导磁的径向偏导:
(15)
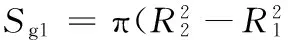
2.2磁环和磁柱间的磁通
对于永磁体和气隙组成的磁路,根据磁路基尔霍夫第一定律和第二定律有
(16)
式中,Bm、Hm分别为永磁体工作点的磁通密度和磁场强度;Bg、Hg分别为气隙处的磁通密度和磁场强度;Sg、Sm分别为气隙处和永磁体中磁路的横截面积;Lg、Lm分别为气隙处磁路长度和永磁体在磁化方向的有效长度;Kf、Kr分别为磁路的漏磁系数和磁阻系数。
永磁材料为烧结钕铁硼,其中保磁力Hc,剩磁Br为已知参数,其退磁曲线近似直线(图3):
Bm=Br(1-Hm/Hc)
(17)
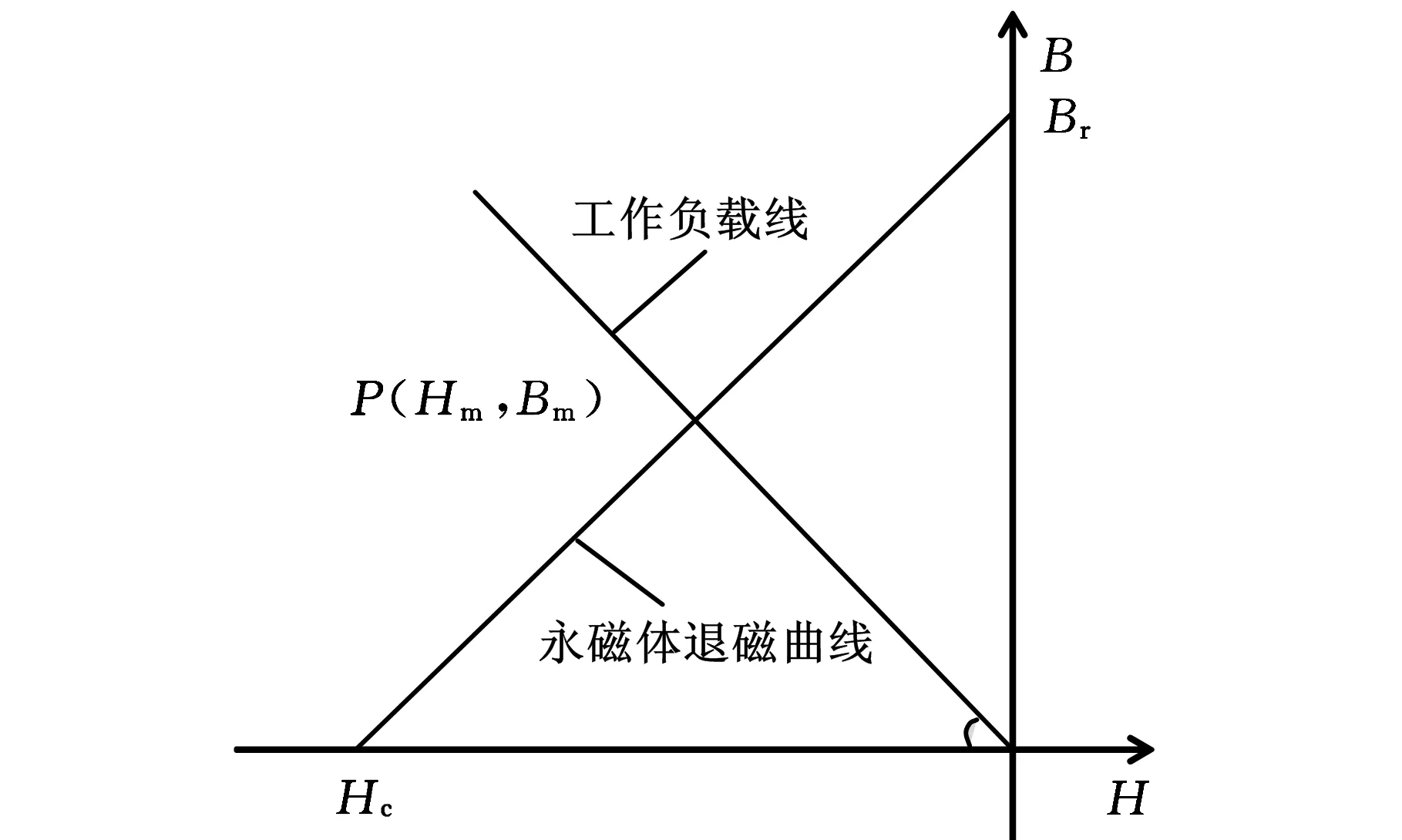
图3 NdFeB永磁体退磁曲线和磁路气隙负载曲线
由式(16)、式(17)得到
(18)
(19)
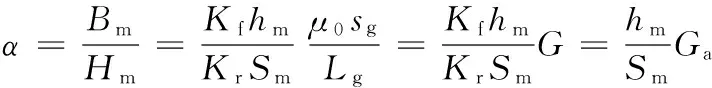
(20)
由式(19)可得磁弹簧中轴线右侧总磁通ΦgR和中轴线左侧总磁通ΦgL:
(21)
2.3径向磁力数学模型
依据磁场理论,磁铁气隙磁能W=Φ2/(2G)。由虚位移法得到径向磁力:
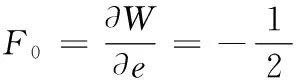
(22)
F=FR-FL
(23)
由上式可知,若z和e一定,则F一定。在平动平面内,沿任意方向移动的位移和沿垂直于平面中心回转的位移相等时,受到的总斥力是相等的,即等刚度。
3 力学特性分析
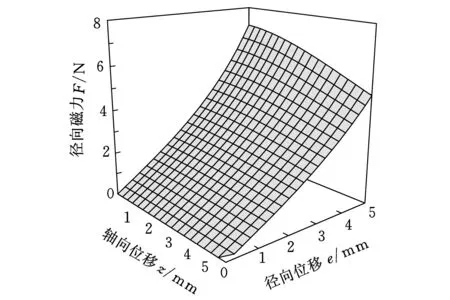
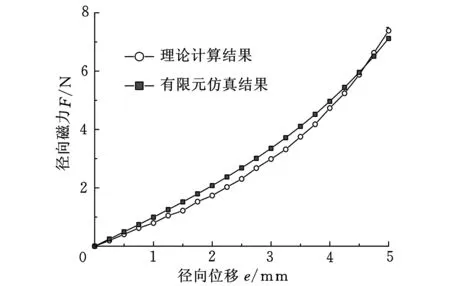
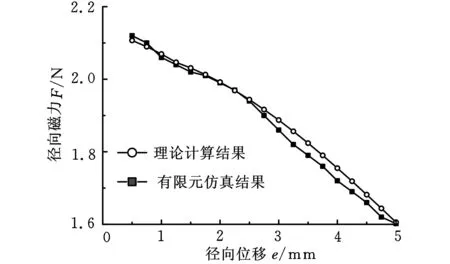
永磁体材料为NdFeBN35H,环形永磁体外径R2=20.5mm,内径R1=14.5mm,柱形永磁体半径r=9mm,环形永磁铁长度L1=4mm,柱形永磁铁长度L2=14mm,永磁体保磁力Hc=-880 000A/m,空气磁导率μ0=4π×10-7H/m,轴向位移0 3.1工作区域判定 为了判定本永磁弹簧的工作区域,利用电磁场有限元仿真软件,对该永磁弹簧一组永磁体进行了仿真分析。 环形永磁体和柱形永磁体径向、轴向的相对位置不同时,径向磁力变化如图4所示,图中,轴向位移为0的位置是柱形永磁体下底面与环形永磁体上顶面重合的位置。由仿真结果可知,随着柱形永磁体和环形永磁体的轴向位置从负变到正并逐渐增加,径向磁力也由负变到正,达到峰值后,缓慢下降。磁弹簧工作磁力应为径向磁力为正值的情况,在考虑磁弹簧过载时,柱形永磁体和环形永磁体不发生碰撞,磁弹簧工作区域选为轴向位移z大于0的位置。 图4 径向磁力与轴向位移关系曲线 3.2径向磁力与径向和轴向位移关系的计算分析 由式(23)可知,径向磁力是径向位移e和轴向位移z的复杂函数,不能直观看出其力学特性,将永磁弹的参数代入数学模型,计算分析其力学特性。当轴向位移z从0.5 mm变化到5.5 mm,径向位移从0变化到5 mm时,径向磁力F的计算结果如图5所示。由图5可知,径向磁力F随着轴向位移z增大而减小。这是由于气隙随轴向位移z增大而增大,磁场强度随之减小。由曲线斜率可知,径向刚度随轴向位移z增大而减小,径向磁力随着径向位移e的增大而增大。 图5 径向磁力与轴向、径向位移的关系 3.3力学特性的有限元验证 对比分析永磁弹簧一组永磁体的径向磁力和径向位移关系的有限元仿真结果和理论计算结果。仿真与理论计算中采用的永磁体为钕铁硼N35H,轴向间距z为0.5 mm。由图6可知,径向磁力F随永磁体径向位移的增加而增大。径向位移较小时,径向磁力与径向位移近似成线性关系,且弹簧刚度约为0.99 N/mm。从图6还可看出,理论计算与仿真结果之间存在误差,其原因在于数学模型没有考虑其他部分磁阻对磁路影响。径向磁力的理论计算与仿真分析结果的平均误差在0.201 N以内,最大误差为0.399 N。 图7表示径向位移e为2 mm时,径向磁力F 图6 径向磁力与径向位移关系 图7 径向磁力与轴向位移关系 随着环形永磁体和柱形永磁体间轴向距离z变化情况。从结果可以看出,永磁体间轴向间距逐渐增大时,径向磁力F逐渐减小,其刚度系数随之减小。 本文提出了一种三自由度等刚度永磁弹簧。磁弹簧的等刚度条件是每组永磁体的环形永磁铁和柱形永磁铁同轴,相同磁级相对布置且轴向存在一定气隙;三组永磁体沿磁弹簧中心对称分布。永磁弹簧在平面内的工作区域是磁弹簧形变量不超过环形磁铁与柱形磁铁的半径差的区域。对永磁弹簧径向斥力进行了理论计算,并利用有限元软件进行了分析计算。计算结果表明:在平动平面内,径向位移一定的情况下,此磁弹簧在3个自由度上的刚度相等。径向磁力随着径向位移的增大而减小,在径向位移较小时,径向磁力与径向位移近似成线性关系。径向磁力和刚度系数随轴向位移的增大而减小。 [1]Xi Qian Kun,Zeng Pei,Min Ru Wei,et al.Novel Magnetic Spring and Magnetic Bearing[J].IEEE Transactions on Magnetics,2003,39(1):559-561. [2]Robertson W,Cazzolato B,Zander A.A Multipole Array Magnetic Spring[J].IEEE Transactions on Magnetics,2005,41(10):3826-3828. [3]杨红,赵韩.稀土永磁弹簧的力学特性研究[J].农业机械学报,2003,34(1):111-117. Yang Hong,Zhao Han.Study on Dynamic Characters of Rare Earth Permanent Magnetic Spring[J].Transactions of the Chinese Society for Agricultural Machinery,2003,34(1):111-117. [4]刘雪箐,白志红,熊光煜.永磁弹簧的设计与计算分析[J].太原工业大学学报,2004,35(3):349-351. Liu Xuejing,Bai Zhihong,Xiong Guangyu.Calculation of Permanent Magnets Spring[J].Journal of Taiyuan University of Technology,2004,35(3):349-351. [5]高海波,邓宗全,胡明,等.行星轮式月球车移动系统的关键技术[J].机械工程学报,2005,41(12):156-161. Gao Haibo,Deng Zongquan,Hu Ming,et al.Key Technology of Moving System of Lunar Rover with Planetary Wheel[J].Chinese Journal of Mechanical Engineering,2005,41(12):156-161. [6]张云鹏,刘淑琴,李红伟,等.基于磁路分析的轴向混合磁轴承径向承载力解析计算[J].电工技术学报,2012,27(5):137-142. Zhang Yunpeng,Liu Shuqin,Li Hongwei,et al.Calculation of Radial Electromagnetic Force of Axial Hybrid Magnetic Bearing Based on Magnetic Circuit Analysis[J].Transactions of China Electrotechnical Society,2012,27(5):137-142. [7]孙立军,张涛,赵兵.永磁磁轴承数学模型的研究[J].机械工程学报,2005,41(4):69-74. Sun Lijun,Zhang Tao,Zhao Bing.Study of Mathematical Model of Permanent Magnet Bearings[J].Chinese Journal of Mechanical Engineering,2004,41(4):69-74. [8]汤双清,蔡敢为,杨家军,等.一种新型被动磁悬浮轴承的研究[J].中国机械工程,2002,13(4):2134-2136. Tang Shuangqing,Cai Ganwei,Yang Jiajun,et al. Study on a New-type Passive Magnetic Bearing[J].China Mechanical Engineering,2002,13(4):2134-2136. [9]田录林,李言,安源,等. 轴向放置轴向磁化的双环永磁轴承径向磁力研究[J]. 中国机械工程,2007,18(24): 2926-2929. Tian Lulin,Li Yan,An Yuan,et al.Research on the Radial Magnetic Force of Axial Placement and Axial Magnetization Bi-annular-shaped PMB[J].China Mechanical Engineering,2007,18(24):2926-2929. [10]田录林,李言,田琦,等. 轴向放置的轴向磁化多环永磁轴承径向磁力研究[J]. 中国机械工程,2008,19(10):1163-1166. Tian Lulin,Li Yan,Tian Qi,et al.Research on the Radial Magnetic Force of Axial Placement and Axial Magnetization Multiannul-shaped Permanent Magnetic Bearings[J].China Mechanical Engineering,2008,19(10):1163-1166. (编辑张洋) Study on Mechanics Characteristics of 3-DOF Same-stiffness Permanent Magnetic Spring Sun FengZhang MingSun XingweiJin JunjieLi QingLi DianqiWang Ke Shenyang University of Technology,Shenyang,110870 This paper presented a 3-DOF same stiffness permanent magnetic spring.According to the structure,the mathematical model of permanent magnetic spring was set by virtual displacement method.The model of the spring’s radial magnetic force was calculated by the mathematical model and FEM software,the calculated results are basically in agreement with the simulation results.The results show that the radial magnetic force of the permanent magnet spring increases with increasing the radial displacement,decreases with increasing the axial displacement. In translational plane,the stiffness coefficients of two moving directions and the rotational direction are equal. When the radial displacement is small, the relationship between the radial displacement and spring stiffness coefficient is approximately linear. same-stiffness;permanent magnetic spring;radial magnetic force;finite-element method(FEM) TH135DOI:10.3969/j.issn.1004-132X.2015.08.003 2014-05-07 国家自然科学基金资助项目(51105257);辽宁省高等学校杰出青年学者成长计划资助项目(LQJ2014012) 孙凤,男,1978年生。沈阳工业大学机械工程学院副教授、博士。主要研究方向为磁悬浮技术与数控技术。发表论文50余篇。张明,男,1988年生。沈阳工业大学机械工程学院硕士研究生。孙兴伟,女,1970年生。沈阳工业大学机械工程学院教授、博士。金俊杰,女,1982年生。沈阳工业大学机械工程学院博士研究生。李清,男,1990年生。沈阳工业大学机械工程学院硕士研究生。李殿起,男,1968年生。沈阳工业大学机械工程学院副教授、博士。王可,男,1957年生。沈阳工业大学机械工程学院教授、博士研究生导师。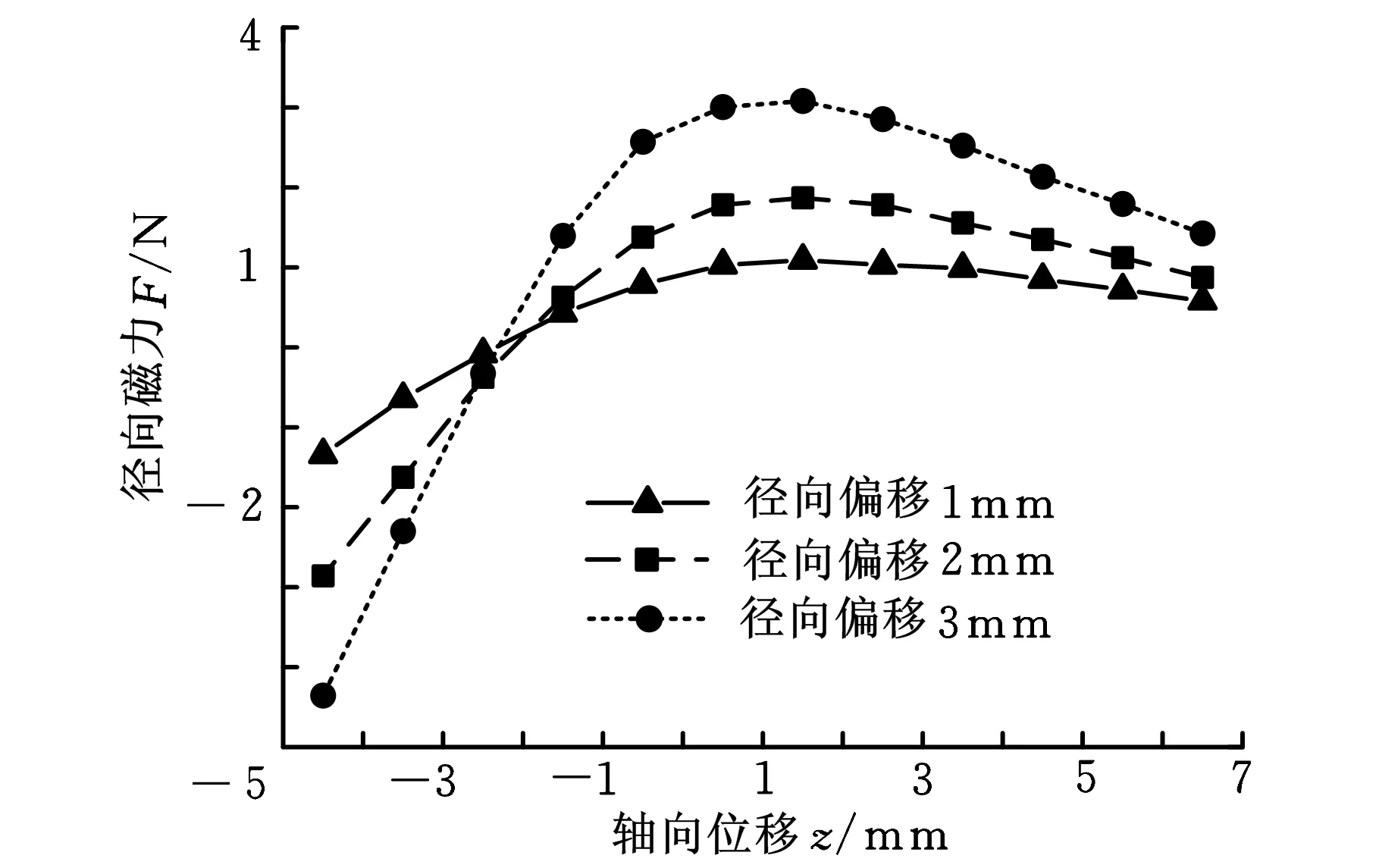
4 结语

