垂直平面三杆柔性机械手动力学建模及仿真
田 颖 张建华 张明路
河北工业大学,天津,300130
垂直平面三杆柔性机械手动力学建模及仿真
田颖张建华张明路
河北工业大学,天津,300130
为解决柔性机械手动力学建模常用的有限元等方法导致模型精度不高的问题,将柔性机械手视为连续整体,用矢量法建立了机械手的动力学模型。对比了矢量法和FEM法建立的动力学模型以及理想状态下机械手刚体动力学模型的仿真结果。对比结果表明,用矢量法建立的柔性机械手动力学模型是可行的,精度也较高。
柔性机械手;矢量法;动力学;Lagrange方程
0 引言
机械手柔性对其末端运动轨迹有一定影响,并且机械手杆件越长,柔性变形越不可忽略。因此对轻质柔性机械手的研究成为机器人领域研究的热点。对于由轻质杆件组成的机械臂来说,常用的动力学研究方式分为三种:质量集中法、假定模态法(AMM)与有限元法(FEM)。
质量集中法是建立柔性机械手动力学模型的最简单方法,但建立的模型精度较低。AMM与FEM的核心思想是将杆件离散为有限个刚性体组成的系统,使用这两种方法建立的动力学模型其精度较质量集中法有所提高,但应用范围较小[1]。Priyanka等[2]使用AMM进行了单杆机械手动力学分析,用浮动切线坐标系定义杆件上的点位置,并给出了仿真结果。但该方法仅适合于简单机械手系统,多用于单杆匀质机械手。杆件数目增加或是杆件截面不规则时,确定模态难度很大,AMM不再适用。FEM与AMM相比,其适用范围有所扩大。Shin等[3]阐述了应用FEM的两杆机械手的动力学建模过程,但未能进行仿真。Wen[4]研究了三杆及三杆以上机械手的动力学分析,给出了仿真结果。FEM的缺点在于它的精度依然不高,而且该方法适宜在平面运动的机械手,不能满足空间机械手的建模要求。Vicente等[5]应用矢量法对单杆机械手进行动力学分析,并以此为基础进一步建立了控制模型,验证了该方法的可行性。Masoud等[6]从建立数学模型的角度证明了矢量法应用于三杆以上的多杆机械手的动力学分析的可行性,但是仅针对多杆机械手中的某一杆件进行了仿真实验,没有得出以多杆机械手作为整体的机械手系统仿真结果。本文针对以上情况,以垂直平面三杆机械手为例,讨论如何应用矢量法建立柔性机械手动力学模型,并通过仿真对比验证分析柔性机械手运动情况。
1 垂直平面三杆柔性机械手的简化
本文以匀质刚性铰接的三杆机械手为例,对其进行简化。由于机械手运动过程中的纵向变形和扭曲变形远小于横向变形,可以认为杆件只有横向变形,且变形前后杆件两端直线距离保持不变。图1所示为垂直平面三杆机械手简化模型。其中,θ1、θ2、θ3分别为理想刚性臂与水平地面的夹角;M1、M2、M3分别为第一关节、第二关节和末端的负载;L1、L2、L3分别为三连杆的长度;τ1、τ2、τ3为机械臂的转矩。从图1可以看出,机械手的独立坐标变量应当包括θ1、θ2、θ3和各杆件的横向变形。
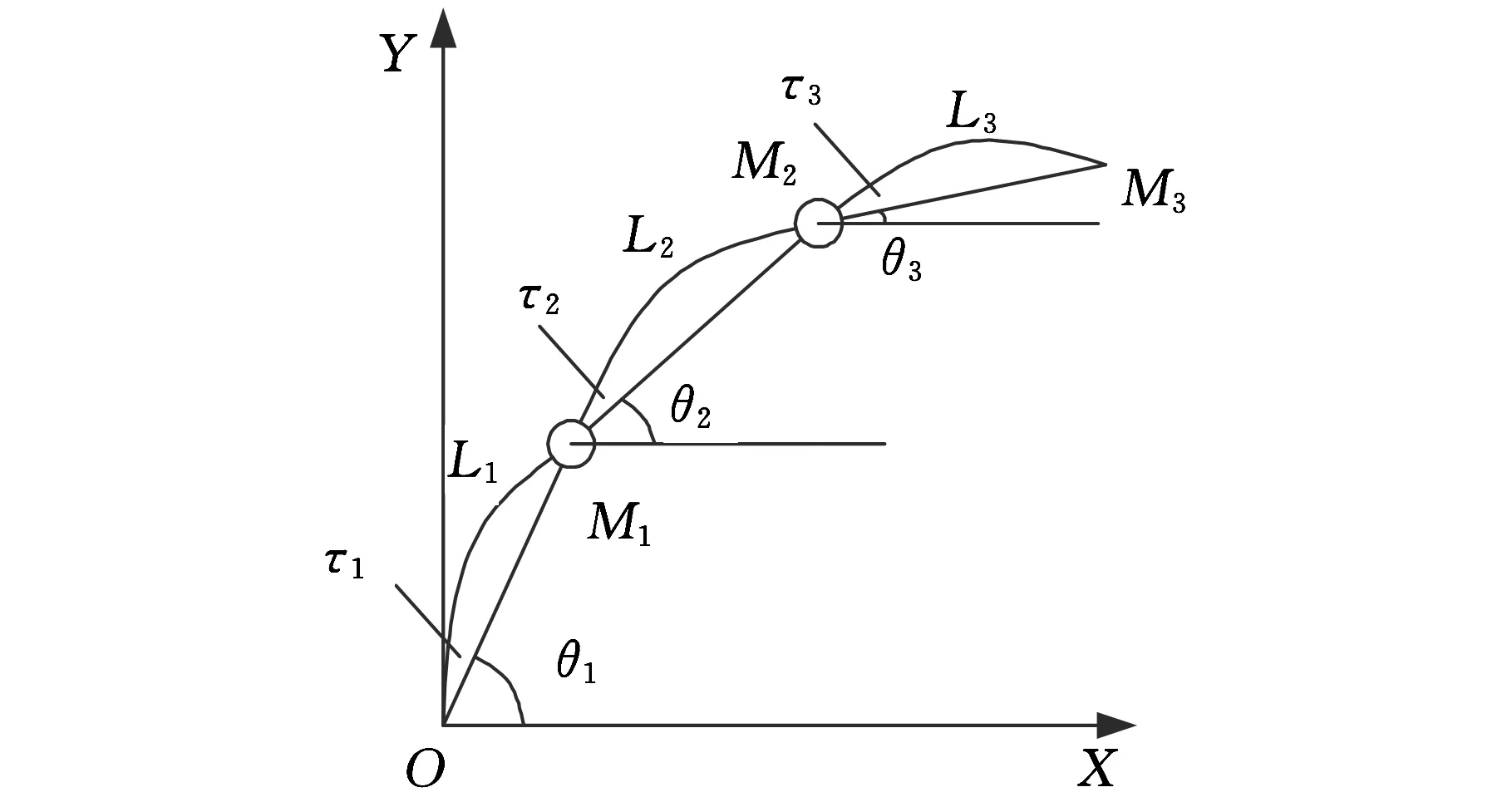
图1 三杆机械手简化模型
2 矢量法的机械手动力学模型
2.1柔性机械手能量计算
FEM和AMM法对柔性机械手的动能和势能的处理如下:先将柔性构件离散为有限个刚性构件,再将刚性构件的能量分别计算累积求和,因此在离散过程中会产生一定的误差。矢量法将杆件视为柔性整体,从源头上避免了这一问题的出现。
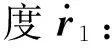
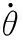
则杆1的动能为
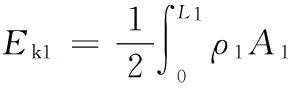
(1)
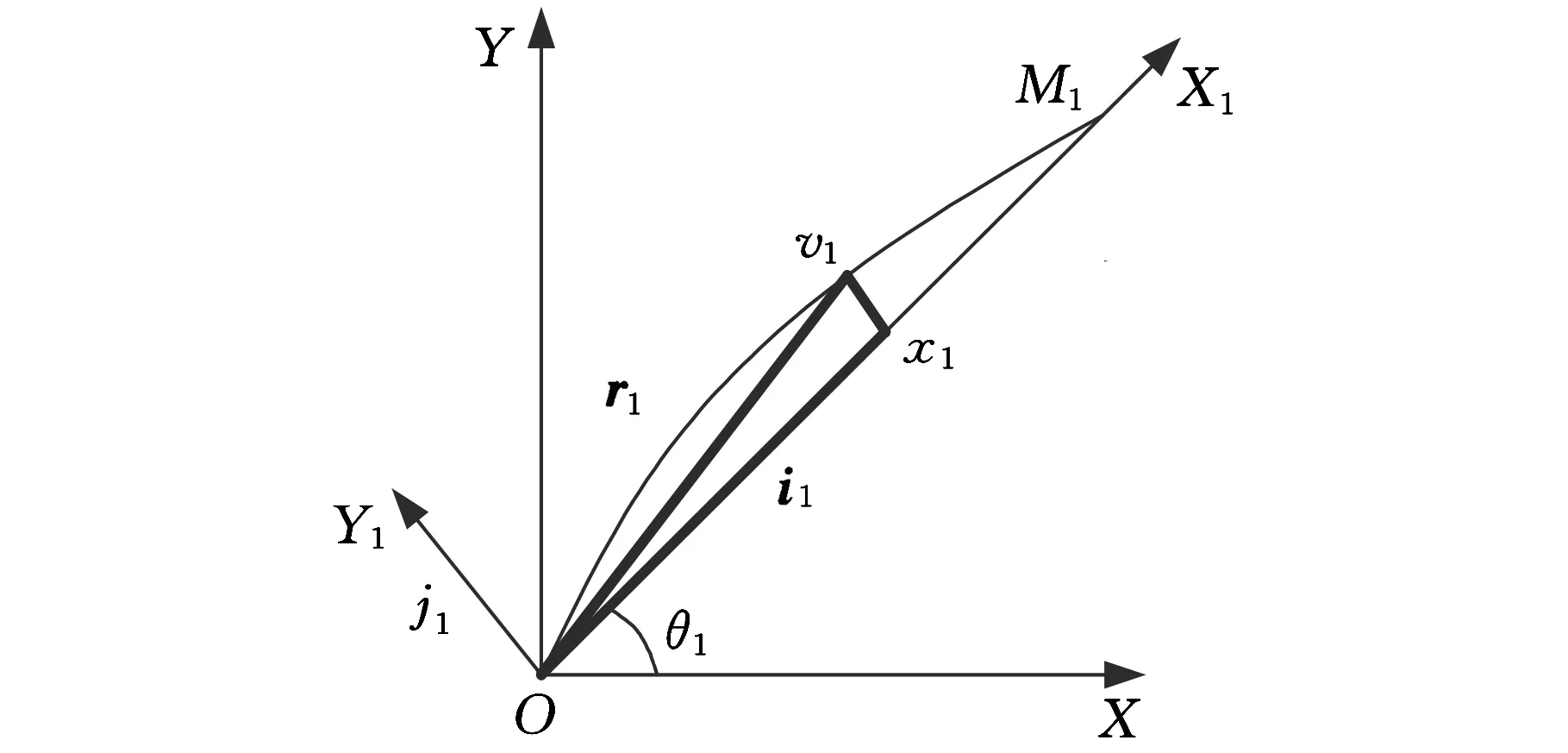
图2 杆1弹性变量示意图
图3中杆2任一点矢量表示为
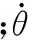
则杆2的动能为
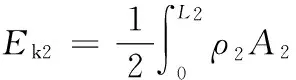
(2)
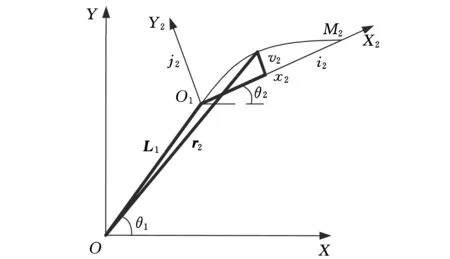
图3 杆2弹性变量示意图
依此类推,杆3的任一点矢量为
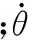
杆3的动能为
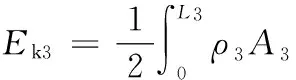
(3)
式(1)~式(3)中,单位向量的运算关系满足:
k,m=1,2,3且k≠m
则柔性机械手系统的动能之和为
Ek=Ek1+Ek2+Ek3
(4)
第i(i=1,2,3)杆的弹性势能为
(5)
vi=φi1(xi)qi1+φi2(xi)qi2
φij(xi)=sin(jπxi/Li)i=1,2,3;j=1,2
式中,EiIi为第i杆的弯曲刚度;vi为第i杆上任一点的横向变形;φi j(xi)为振型函数,下标i、j分别表示第i杆和j阶弹性模量;qi1、qi2分别为一阶和二阶弹性模态的时间函数,与杆件转动角度一起,组成了矢量法中的独立坐标变量。
基于以上弹性势能公式的推导,可得三杆机械手弹性势能之和:
Ep=Ep1+Ep2+Ep3
(6)
平面三杆柔性机械手的重力势能简化为每杆重力等效在变形后的杆件中点产生的重力势能。则杆1的重力势能为
W1=(m1|r1(L1/2)|+M1L1)gsinθ1
(7)
杆2的重力势能为
W2=m2gsin(θ1+θ2)|r2(L2/2)|+
M2g(L1sinθ1+L2sinθ2)
(8)
杆3的重力势能为
W3=m3gsin(θ1+θ2+θ3)|r3||x3=L3/2+
M3g(L1sinθ1+L2sinθ2+L3sinθ3)
(9)
三杆机械手系统的重力势能为
W=W1+W2+W3
(10)
由于柔性机械臂是一个非保守系统,其能量公式可应用于Lagrange方程:
(11)
L=Ek-(Ep+W)
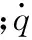
机械手系统独立坐标变量为
在不考虑重力的影响下,系统所作的虚功为
(12)
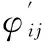
通过式(12)可以求得系统广义力Qn。
2.2三杆机械手动力学方程的符号推导
式(11)经过整理后,可得柔性机械手的显式动力学方程:
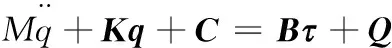
(13)
L1L2(M2+2m3+M3)cos(θ1-θ2)-
m2L1L2(2q21+q22)sin(θ1-θ2)/π
m51=m15=-2ρ2A2l1cos(θ1-θ2)
m71=m17=(m3L3+M3)L1L3cos(θ1-θ3)-
m3L1L3(2q31+q32)sin(θ1-θ3)/π
m81=m18=-2m3L1L3cos(θ1-θ3)/π
m91=m19=-m3L1L3cos(θ1-θ3)/π
m22=m33=m1L1
m47=m74=L2L3(m3L3+M3)cos(θ2-θ3)-
m3L2L3(2q31-q32)sin(θ2-θ3)/π
m48=m84=-2m3L2L3cos(θ2-θ3)/π
m49=m94=-m3L2L3cos(θ2-θ3)/π
m55=m66=m2L2
m88=m99=m3L3
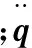
3 刚性机械手动力学建模
垂直平面三杆刚性机械手自由度为3,其广义坐标变量
qg=[θ1gθ2gθ3g]T=[q1gq2gq3g]T
刚性三杆机械手动能为
(14)
三杆刚性机械手势能为
Wg=(m3/2+M3)gL3sinθ3g+
(m2/2+m3+M2+M3)gL2sinθ2g+
(m1/2+m2+m3+M1+M2+M3)gL1sinθ1g
(15)
由于刚性机械臂是一个非保守系统,其能量公式可应用于Lagrange方程:
(16)
Lg=Ekg-Wg
整理式(16)可得三杆刚性机械手的显式动力学方程:
(17)
mg33=m3L3
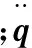
4 仿真结果比较与分析
通过比较矢量法、FEM法建立的柔性机械手动力学模型和刚性机械手动力学模型仿真结果,可以判断矢量法的可行性并定性分析矢量法建模的精度。
表1所示为柔性三杆机械手的仿真参数,除弯曲刚度EiIi外,其余仿真参数也应用于刚性三杆机械手的仿真。
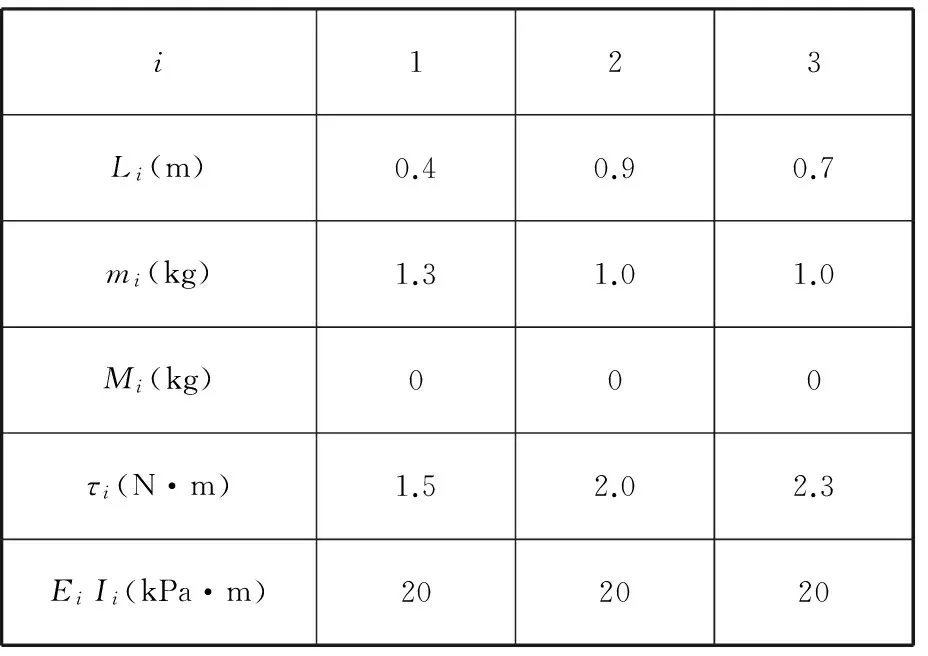
表1 三杆机械手参数值
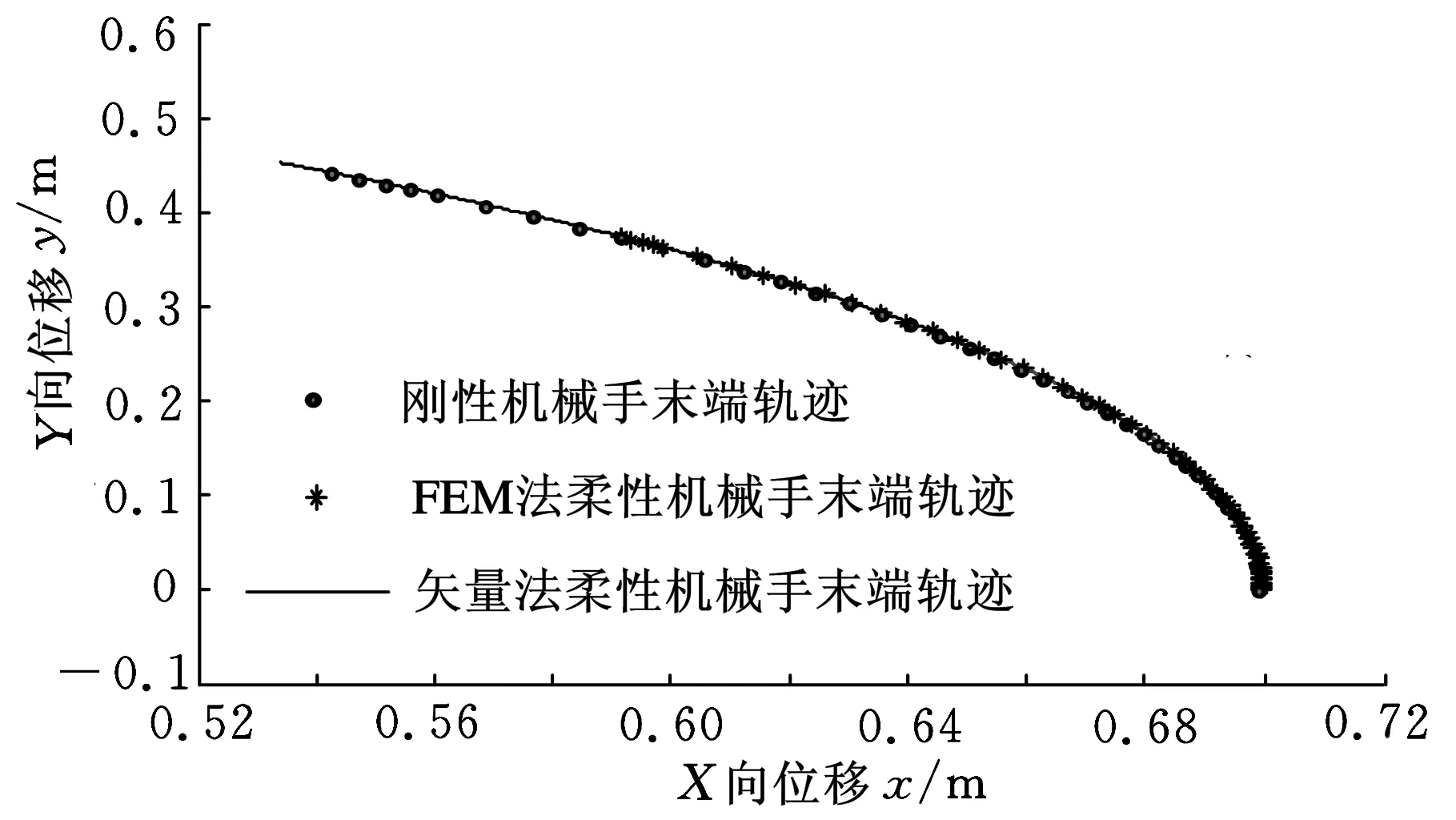
图4 柔性与刚性机械手末端运动轨迹
图4所示为使用矢量法、FEM法的柔性机械手末端运动轨迹仿真结果与理想刚性机械手末端运动轨迹仿真结果。由图4可以看出,在表1所示条件下,机械手的柔性变形较大,不可忽略。矢量法和FEM法的轨迹较为吻合,证明矢量法可行。
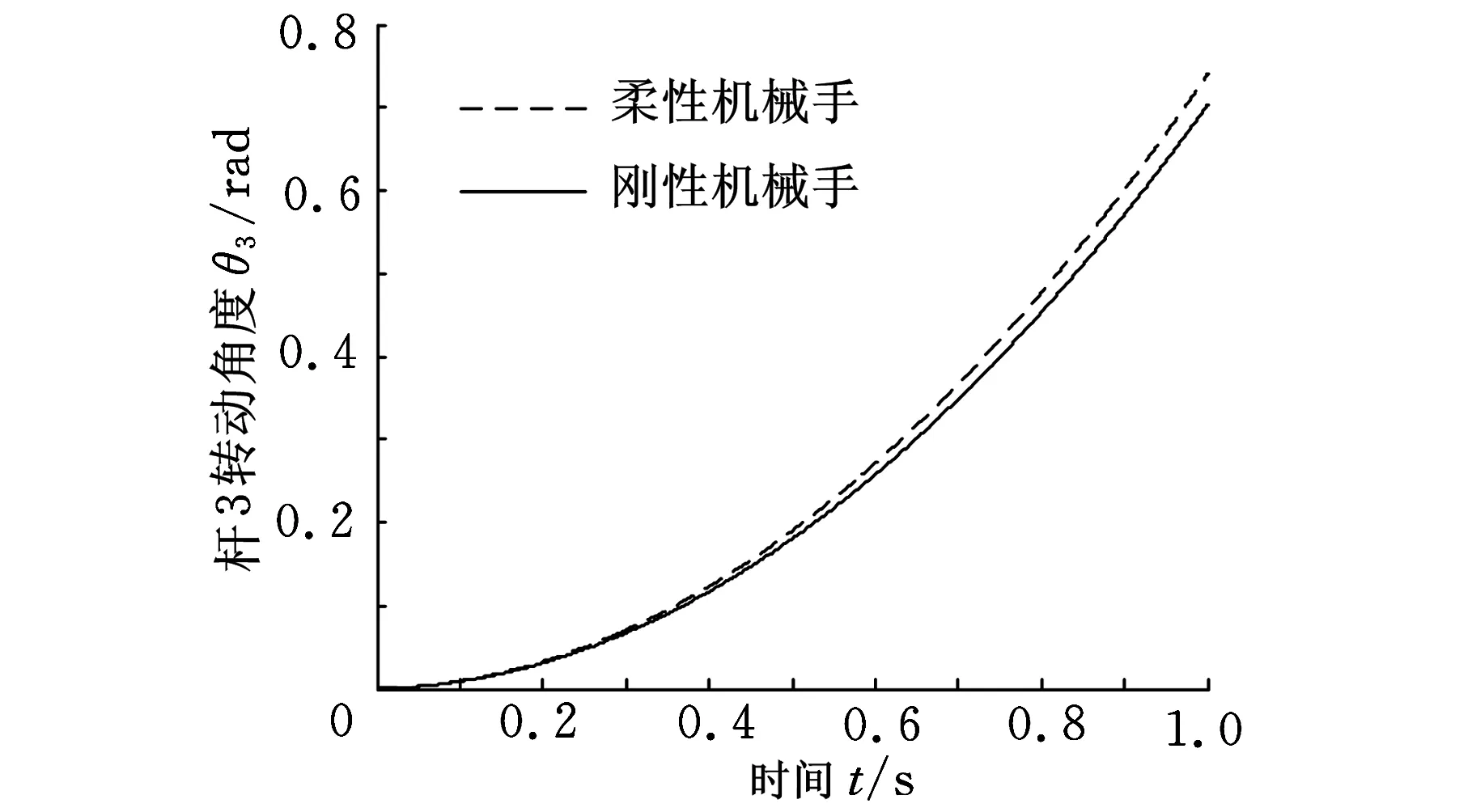
图5 杆3的转动角度仿真结果
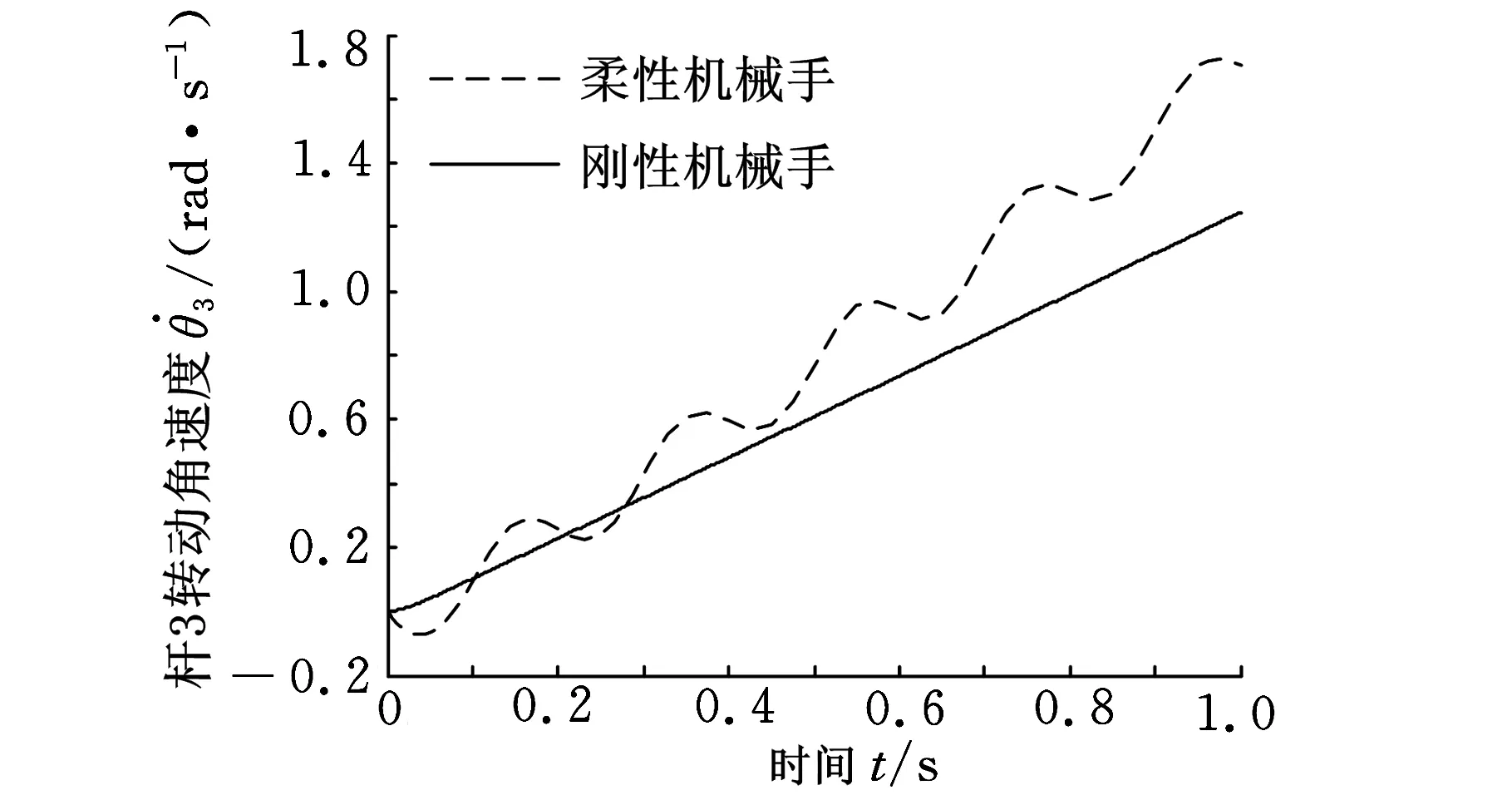
图6 杆3的转动角速度仿真结果
由图7、图8可以看出,柔性机械手的横向变形较小,最大值小于0.4mm,这符合机械手实际运动情况。对于刚度较大的杆件材料和结构,其弹性变形较小,通常情况下可以忽略,但对于高精度要求下的机械手作业,该变形不能忽略。
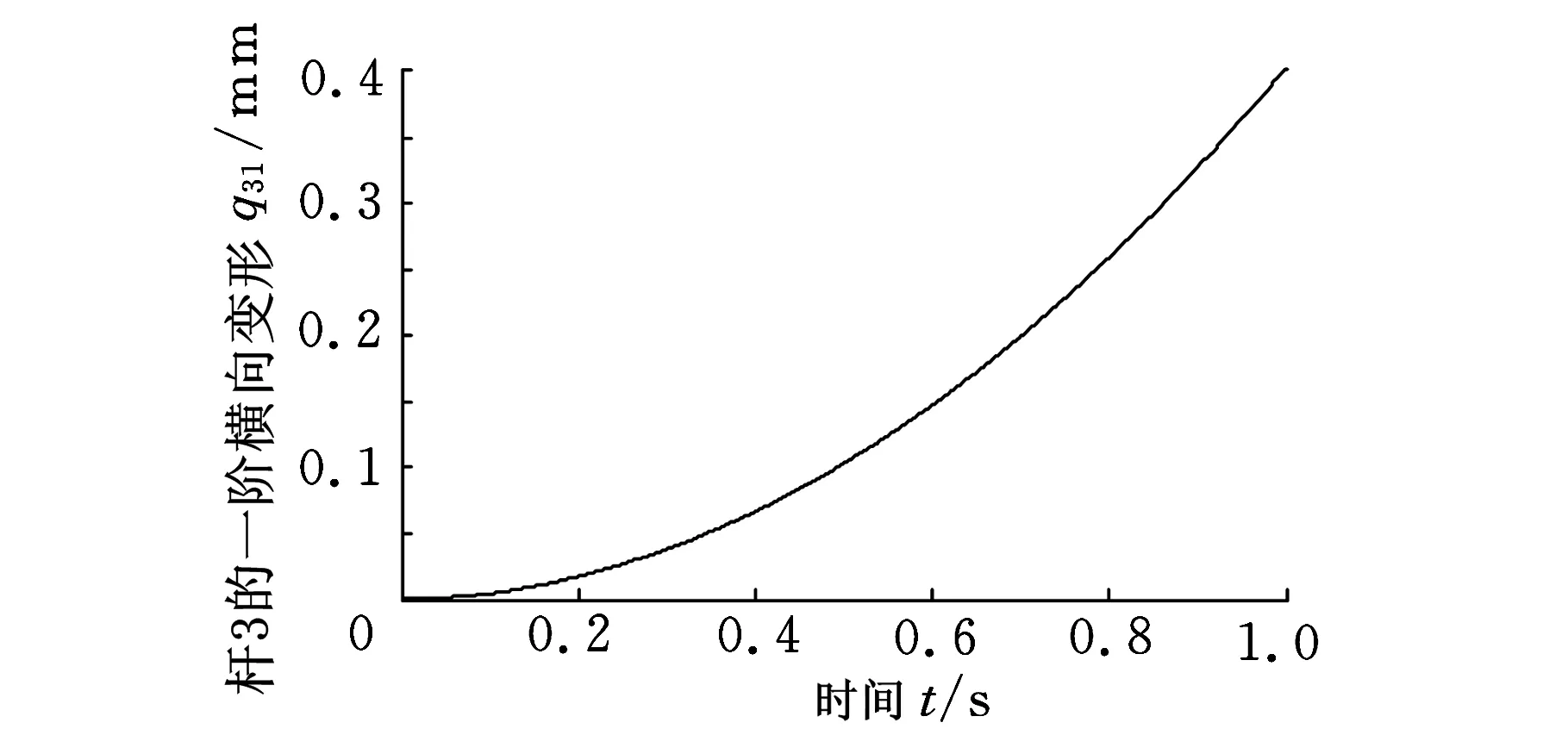
图7 柔性机械手杆3的一阶横向变形
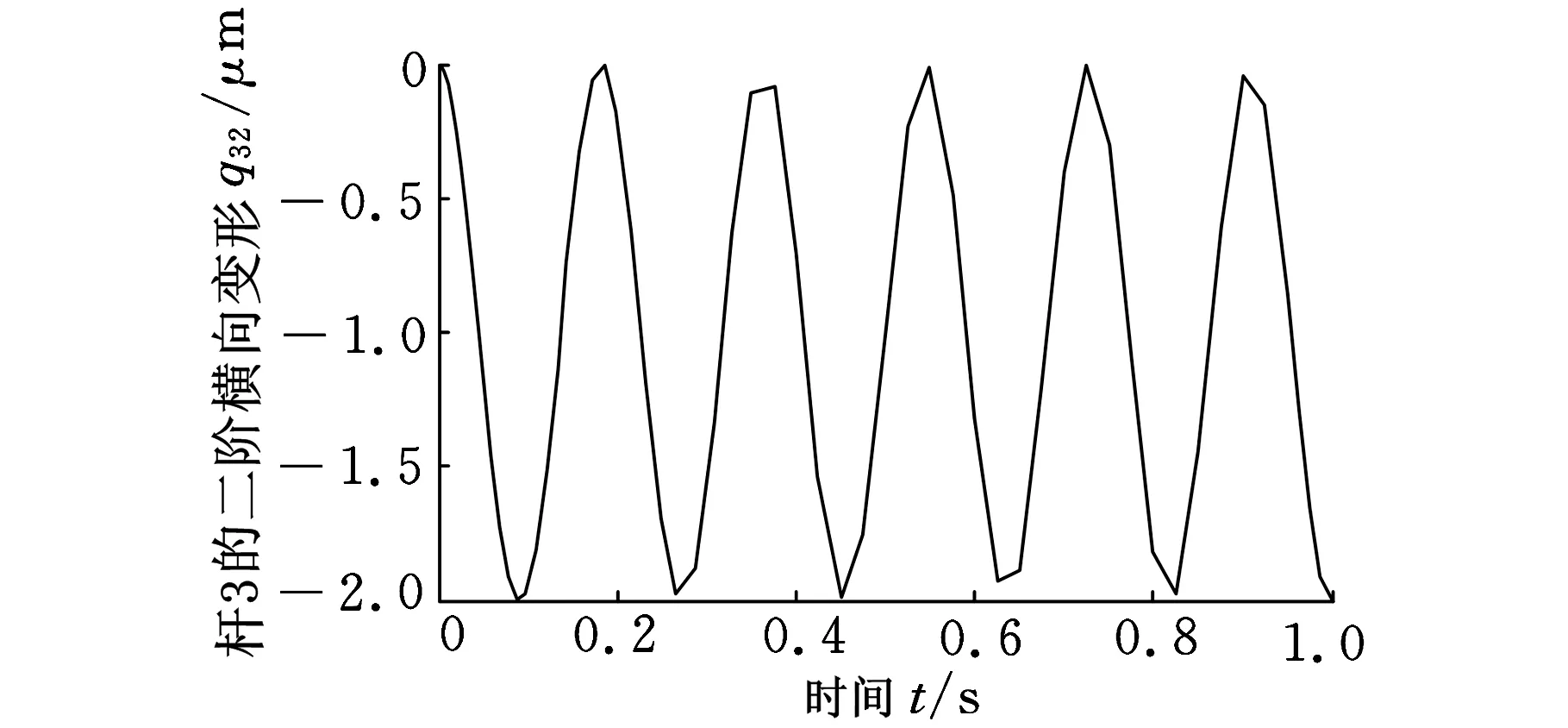
图8 柔性机械手杆3的二阶横向变形
5 结语
用矢量法建立的垂直平面三杆柔性机械手系统的动力学模型,具有计算精度高、计算复杂程度低的特点。刚性机械手和柔性机械手的仿真结果对比证明了该模型的可行性。柔性机械手的仿真结果还表明,对于刚度较小、精度要求较高的柔性机械手,其柔性变形已不能忽略,机械手系统如果继续作为理想刚性机械手处理会引起较大误差。
但矢量法也有其缺点,由第二节建立动力学模型的过程可以看出,大量的符号运算提高了计算精度,但导致数据的计算较为繁琐,如何在提高模型精度的基础上进一步简化计算过程,是矢量法建模今后的研究方向。
[1]Santosha K D,Peter E.Dynamic Analysis of Flexible Manipulators,a Literature Review[J].Mechanism and Machine Theory,2006,41(7):749-777.
[2]Priyanka M,Qiao Sun,Yoshikazu Kanamiya.A Pseudo-rigid Model for the Inverse Dynamics of an Euler Beam[J].Applied Mathematical Modelling,2011,35(8):3854-3865.
[3]Shin Ho-Cheol,Choi Seung-Bok.Position Control of a Two-link Flexible Manipulator Featuring Piezoelectric Actuators and Sensors[J].Mechatronics,2001,11(6):707-729.
[4]Wen Chen.Dynamic Modeling of Multi-link Flexible Robotic Manipulators[J].Computers and Structures,2001,79(2):183-195.
[5]Vicente F,Emiliano P,Iván M D.Passivity-based Control of Single-link Flexible Manipulators Using a Linear Strain Feedback[J].Mechanism and Machine Theory,2014,71:191-208.
[6]Masoud M,Mostafa G,Mohammad J S.A Nonlinear High Gain Observer Based Input-output Control of Flexible Link Manipulator[J].Mechanics Research Communications,2012,45:34-41.
(编辑张洋)
Dynamics Modeling and Simulation of Three-link Flexible Manipulator on Vertical Plane
Tian YingZhang JianhuaZhang Minglu
Hebei University of Technology,Tianjin,300130
For solving problem of lower accuracy induced by common methods in flexible manipulator dynamics modeling,such as FEM etc.,flexible manipulator was considered as a continuous whole and its dynamics model was built by vector method.Simulation results of dynamics model of flexible manipulator under vector method and FEM,and dynamic model of ideal rigid manipulators were compared to prove that vector method is effective and more accurate.
flexible manipulator;vector method;dynamics;Lagrange equation
2013-09-09
TH113.22DOI:10.3969/j.issn.1004-132X.2015.08.005
田颖,女,1987年生。河北工业大学机械工程学院博士研究生。主要研究方向为机器人动力学及控制。张明路,男,1964年生。河北工业大学机械工程学院教授、博士研究生导师。张建华,男,1979年生。河北工业大学机械工程学院副教授。

