一种疲劳-蠕变交互作用寿命预测模型及试验验证

陈　凌　张贤明　欧阳平

重庆工商大学废油资源化技术与装备教育部工程研究中心,重庆,400067

一种疲劳-蠕变交互作用寿命预测模型及试验验证

陈凌张贤明欧阳平

重庆工商大学废油资源化技术与装备教育部工程研究中心,重庆,400067

基于延性耗竭理论和损伤力学，对材料疲劳-蠕变交互作用下的延性消耗、损伤、循环周次和失效寿命之间的关系进行了分析，在此基础上,建立了一种疲劳-蠕变交互作用的寿命预测模型,模型形式简单,非常便于实际工程应用。通过1.25Cr0.5Mo钢光滑试样540℃和520℃环境下应力控制的梯形波加载试验，用该模型进行了失效寿命的预测，可以很好地解释相同温度和加载条件下的寿命波动，预测结果与实测结果符合较好。

疲劳-蠕变;延性;损伤;平均应变;寿命预测

0　引言

随着我国石化、冶金、电力、航空航天等行业的迅速发展，加氢反应器、燃气轮机、高温冶炼装置等设备得到了广泛的应用。这类设备在服役过程中长期承受启动停车、温度波动等工况造成的循环载荷，同时在高温环境下，材料会产生缓慢的黏性流动导致蠕变变形，使设备部件承受疲劳、蠕变的交互作用，引发失效，因此，研究疲劳-蠕变交互作用的寿命预测对高温设备部件的可靠性设计和安全评估具有非常大的工程实际意义。

关于疲劳-蠕变交互作用的寿命预测,国内外学者进行了大量的研究,主要的方法有寿命-时间分数法[1]、频率修正法(FM)[2]、频率分离法(FS)[3]、应变范围划分法(SRP)[4]、应变能划分法(SEP)[5]等经典理论以及一些相应的修正方法[6-8]。这些疲劳-蠕变交互作用的寿命预测方法大都是基于应变控制条件提出的，对于应力控制条件较难适用。针对应力控制条件下疲劳-蠕变交互作用的寿命预测,有学者提出了相应的预测方法[9-11]，这类方法针对特定的工况具有较好的效果,但不能解释材料相同温度和加载条件下的寿命波动，同时形式较为复杂，不便于实际应用。

针对上述情况,本文基于延性耗竭理论和损伤力学，对材料疲劳-蠕变交互作用下的延性消耗、损伤、循环周次和失效寿命之间的关系进行了分析，在此基础上，建立了一种疲劳-蠕变交互作用的寿命预测模型。为验证模型的准确性，进行了1.25Cr0.5Mo钢光滑试样高温环境(540℃和520℃)应力控制的梯形波加载试验，选取各个寿命段的采样数据用该模型进行失效寿命的预测，同时利用该模型对相同温度和加载条件下的寿命波动进行了解释与预测。

1　一种疲劳-蠕变交互作用寿命预测模型

1.1延性耗竭理论

延性是一种物理特性,是指材料在受力产生破坏之前的塑性变形能力。根据延性耗竭理论[12-14],高温环境下,疲劳和蠕变以黏性流的方式产生交互作用,消耗材料延性,使材料产生损伤,当材料延性耗尽时，即累积的延性消耗达到临界值时，材料发生失效。上述理论表明材料的损伤过程伴随着材料的延性消耗,因此,材料的损伤可用材料的延性消耗来表示，即

D=f1(dεf)

(1)

式中,εf为材料延性;D为材料损伤。

另一方面，材料延性与温度密切相关，随着温度升高,晶界参与滑移的程度增加，延性变大，同时材料延性消耗的过程伴随着材料的变形，因此，可用平均应变和温度的函数来表示材料延性的消耗,即

dεf=f2(εm,T)

(2)

式中,εm为平均应变;T为环境温度。

将式(2)代入式(1),可得如下表达式：

D=f1(f2(εm,T))=F(εm,T)

(3)

即材料的损伤可用平均应变和温度的函数来表示,对于特定的温度,材料的损伤为平均应变的函数。

1.2疲劳-蠕变交互作用的损伤理论

根据损伤力学的经典理论[15]：材料或结构内部存在的位错、微裂纹、微空洞等微缺陷，在损伤过程中相互作用、相互影响，造成材料有效承载面积减小，产生损伤，可用有效承载面积的减小定义损伤,即

D=1-S*/S

(4)

式中,S为材料未产生损伤时的有效承载面积;S*为材料产生损伤后的有效承载面积。

根据式(4)的定义，疲劳和蠕变造成的有效承载面积的减小量可直接相加,因此,材料疲劳-蠕变交互作用下的损伤可表示如下：

D=Df+Dc

(5)

式中,Df为疲劳损伤;Dc为蠕变损伤。

由前期研究可知[16],疲劳和蠕变的损伤可分别表示为

Df=Df f-(Df f-Df0)[(1-N/Nf)]α(σ,T)

(6)

Dc=Dcc-(Dcc-Dc0)(1-t/tc)β(σ,T)

(7)

式中,N为循环周次;Nf为疲劳寿命;t为蠕变时间;tc为蠕变失效时间;Df0和Df f为疲劳条件下的初始损伤和失效损伤;Dc0和Dcc为蠕变条件下的初始损伤和失效损伤;α(σ,T)和β(σ,T)为受加载水平σ和环境温度T所决定的材料常数。

对于带保载循环的疲劳-蠕变交互作用,蠕变时间和循环周次的关系、蠕变失效时间和疲劳寿命的关系可分别表示如下：

t=TF-CN

(8)

tc=TF-CNf

(9)

式中,TF-C为一个循环内的保载时间。

同时,对于带保载循环的疲劳-蠕变交互作用,疲劳寿命与失效寿命是一致的,即

Nf=NF

(10)

式中,NF为失效寿命。

将式(6)～式(10)代入式(5),可得

D=(Df f+Dcc)-[(Df f-Df0)(1-N/NF)α(σ,T)+

(Dcc-Dc0)(1-N/NF)β(σ,T)]

(11)

其中,Df f+Dcc=1,即材料失效破坏时损伤为1,代入式(11)可得

D=1-[(Df f-Df0)(1-N/NF)α(σ,T)+

(Dcc-Dc0)(1-N/NF)β(σ,T)]

(12)

由式(12)可知,疲劳-蠕变交互作用下的材料损伤可用变量N/NF和加载工况的函数来表示,即可将式(12)简化为

D=G(N/NF,σ,T)

(13)

1.3疲劳-蠕变交互作用寿命预测模型

由上文可知,基于延性耗竭理论和损伤力学,疲劳-蠕变交互作用下材料的损伤可分别表示为式(3)和式(13)，联立式(3)和式(13)可得

D=F(εm,T)=G(N/NF,σ,T)

(14)

对于特定的加载水平,材料会做出对应的变形反应，因此,式(14)中的加载水平可用平均应变的函数来反应,即

F(εm,T)=G(N/NF,g(εm),T)

(15)

由式(15)可知,N/NF可用平均应变和温度的函数来表示,即

N/NF=H(εm,T)

(16)

εm=a1+b1Nc1

(17)

式中,a1、b1、c1为材料常数。

由式(16)可知，对于特定温度下的疲劳-蠕变交互作用,材料的循环周次与失效寿命的比值和平均应变之间存在对应关系。前期研究表明[17]：在疲劳-蠕变交互作用下,材料的平均应变εm与循环周次N之间呈明显的power函数关系,如下式所示：

对于一个特定试样的失效过程而言,循环周次N是变化量,失效寿命NF是常数,N/NF的变化趋势与N一致。因此，平均应变εm与循环周次N存在式(17)所示的对应关系，则εm与N/NF也必然存在式(17)所示的对应关系,记为

εm=a+b(N/NF)c

(18)

式中,a、b、c为材料常数。

同时由式(16)可知,a、b、c为与温度相关的材料常数，不同的温度对应不同的材料常数。

利用式(18)反算失效寿命,可得下式：

NF=N/[(εm-a)/b]1/c

(19)

特定温度下，对于承受疲劳-蠕变交互作用的材料，当已知循环周次和对应周次下的平均应变，利用式(19)即可得出材料的失效寿命，失效寿命减去已进行的循环周次，即为材料的剩余寿命。

试样疲劳-蠕变交互作用下的失效除受环境温度和加载水平影响外，还与表面及亚表面的夹杂物、缺陷、光滑度等密切相关，相同的工况下，试样的失效寿命可能存在较大的波动。另外，如前所述，材料延性是材料的物理特性，与温度密切相关，加载水平以及试样表面、亚表面存在的夹杂物、缺陷等因素只影响材料延性消耗的快慢，对于材料延性本身没有影响。因此，上述基于延性耗竭理论和损伤力学，利用材料延性的消耗来描述损伤，进而推导得到的寿命预测模型(式(19))，可以很好地适用于相同温度和加载条件下出现寿命波动的情况，具有明确的理论依据，该寿命预测模型形式简单，非常适合实际工程应用。

另外，对于合金钢等金属材料设备的复杂结构应力集中区,可采用von Mises屈服准则计算相应的等效应变，然后取每次加载历程的最小等效应变和最大等效应变的平均值作为等效平均应变，结合式(19)，即可将本文所述寿命预测模型推广至复杂结构应力集中区。

2　试验结果及讨论

试验在岛津电液伺服疲劳试验机上进行，试验材料为1.25Cr0.5Mo珠光体耐热钢，试验温度为540 ℃和520 ℃。按国家标准GB/T 15248-2008《金属材料轴向等幅低循环疲劳试验方法》[18]进行试验,试验采用螺纹夹持的圆棒试样。试验控制方式为应力控制,加载波形为梯形波以引入蠕变保载,加载频率为0.05 Hz,上下保载时间各为5 s。试验中采用高温引伸计自动记录应力和应变。

表1、表2为材料540 ℃、520 ℃下的试验数据,其中Δσ为名义应力范围。加载过程中材料的平均应变εm为每次循环加载过程中的最小应变(梯形波加载初始点)和最大应变(梯形波加载上保载完结点)的平均值。图1、图2为材料540 ℃、520 ℃下平均应变εm随循环周次N的变化图(其中横坐标用N的常用对数表示),图3、图4为材料540 ℃、520 ℃下平均应变εm随循环周次与失效寿命的比值N/NF的变化图(其中横坐标用N/NF的常用对数表示)。

表1　540℃下材料疲劳-蠕变交互作用试验数据

表2　520 ℃下材料疲劳-蠕变交互作用试验数据

图1　540 ℃下平均应变随循环周次变化图

图2　520 ℃下平均应变随循环周次变化图

图3　540 ℃下平均应变随循环周次与失效寿命比值变化图

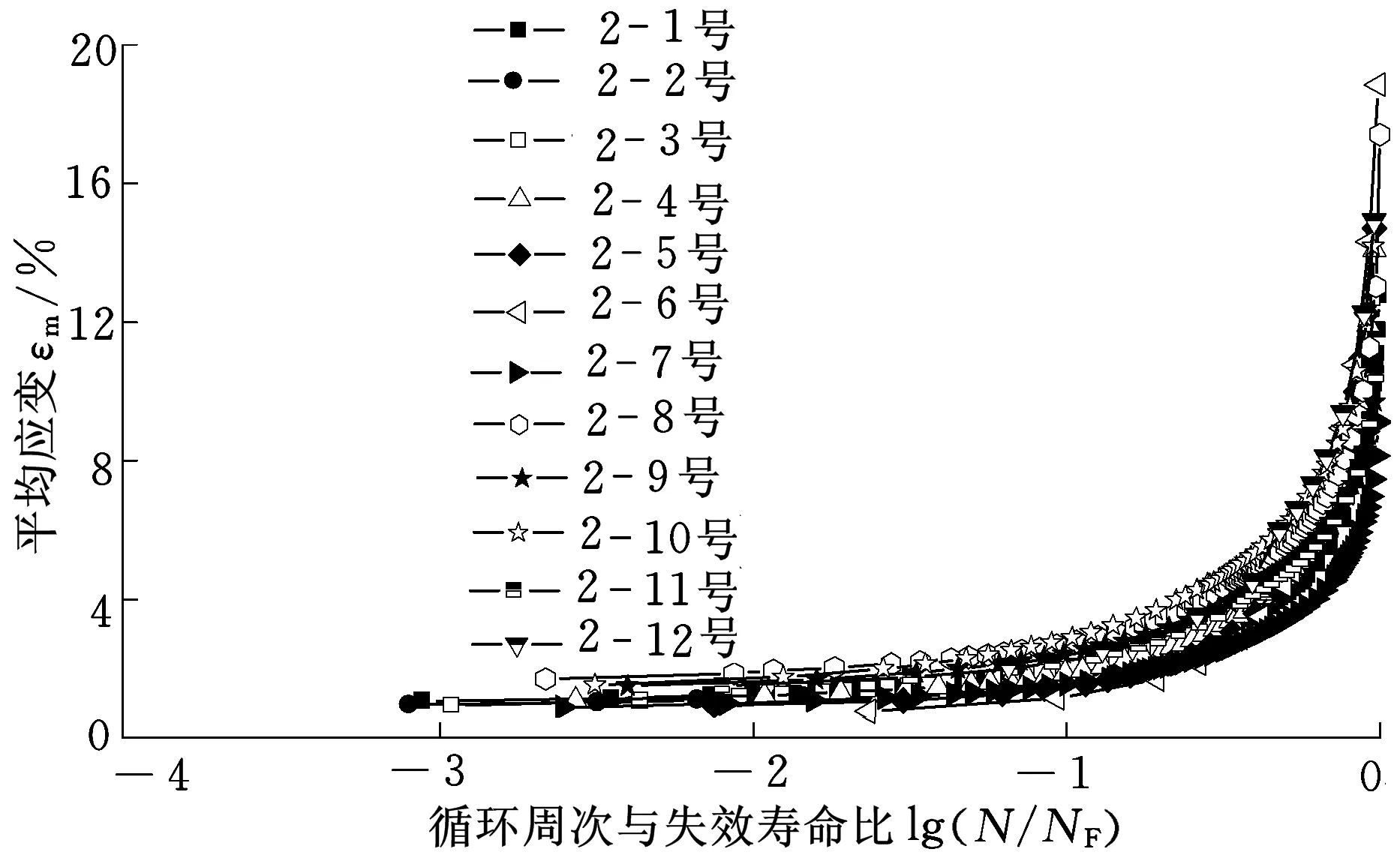
图4　520 ℃下平均应变随循环周次与失效寿命比值变化图

由图1～图4可知:①高温环境疲劳-蠕变交互作用下，材料的平均应变εm随循环周次N的变化趋势呈式(17)所示的power函数形式,同时,540 ℃时的变形量明显大于520 ℃时的变形量,说明温度越高材料延性越大;②相较于εm随N的变化,同一温度不同加载条件下,εm随循环周次与失效寿命的比值N/NF的变化趋势接近一致,说明在特定温度条件下,材料的延性消耗对应的寿命消耗是一定的，利用式(18)可以获得材料不同温度条件下εm与N/NF的对应关系，进而利用式(19)反算材料的失效寿命。

图5　540 ℃下εm与N/NF的对应关系拟合曲线

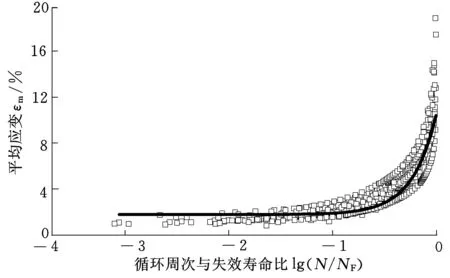
图6　520 ℃下εm与N/NF的对应关系拟合曲线

图5、图6分别为540 ℃、520 ℃时1.25Cr0.5Mo钢疲劳-蠕变交互作用下,εm与N/NF的对应关系(式(18))拟合曲线，其表达式如下：

在540 ℃、R=0.98357时

εm=0.82464+13.93886×(N/NF)2.00288

(20)

在520 ℃、R=0.97673时

εm=1.77938+8.73767×(N/NF)1.86818

(21)

其中,R为曲线拟合相关系数。

利用式(20)、式(21)反算失效寿命，可得到在540 ℃时，有

NF=N/[(εm-0.82464)/13.93886]1/2.00288

(22)

在520 ℃时，有

NF=N/[(εm-1.77938)/8.73767]1/1.86818

(23)

利用式(22)、式(23)，根据不同循环周次对应的平均应变，即可获得失效寿命。分别选取1.25Cr0.5Mo钢540 ℃、520 ℃疲劳-蠕变交互作用下NF/4、NF/2、3NF/4附近对应的循环周次和平均应变采样点,进行失效寿命的预测，预测效果图见图7、图8。

图7　540 ℃下疲劳-蠕变交互作用寿命预测效果图

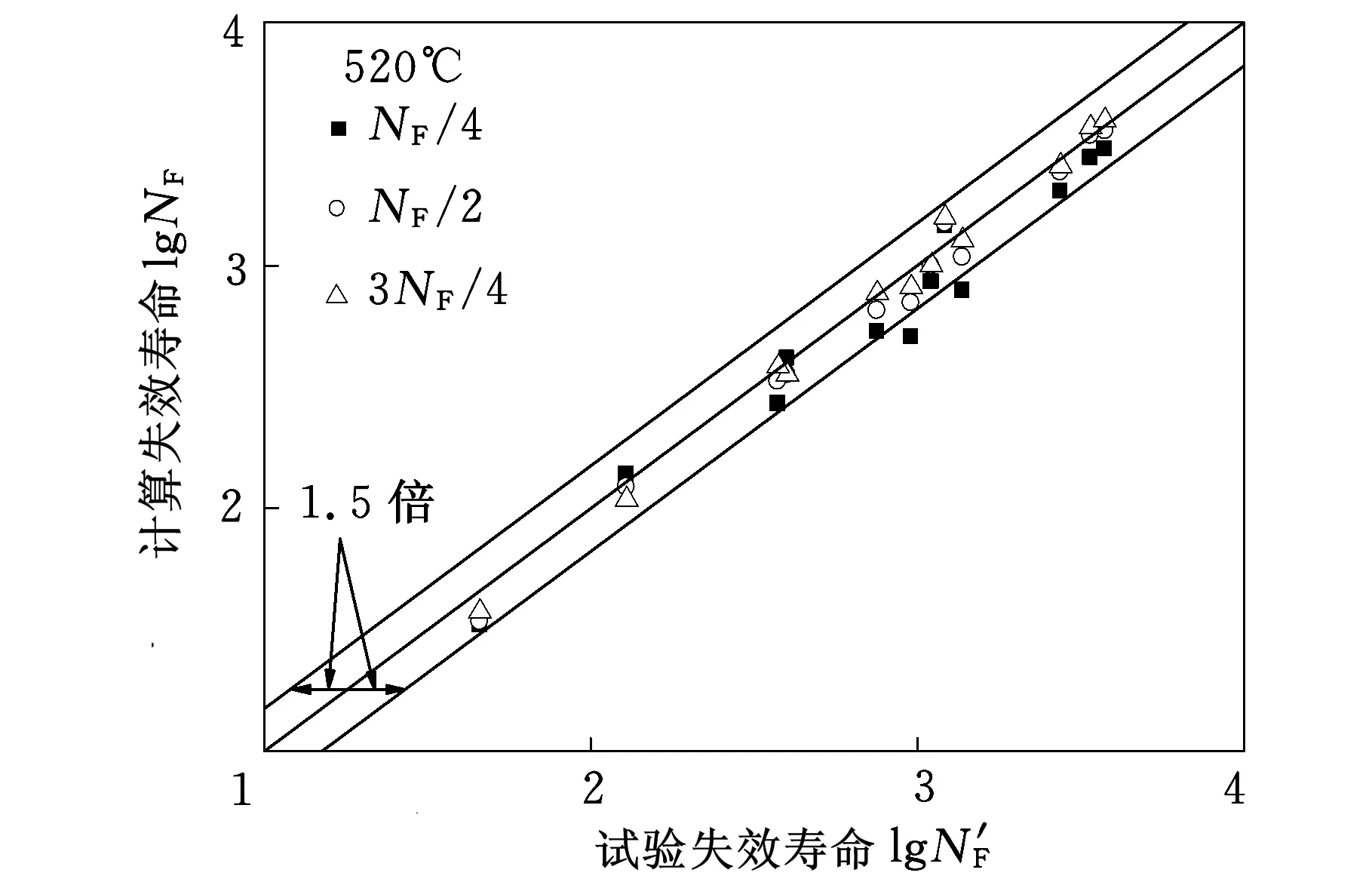
图8　520 ℃下疲劳-蠕变交互作用寿命预测效果图

从图7、图8可以看出，本文提出的疲劳-蠕变交互作用寿命预测模型对于各个寿命段的采样数据均具有较好的预测效果,540 ℃时，93%的数据点位于1.5倍误差带以内,520℃时,94.4%的数据点位于1.5倍误差带以内。同时模型形式简单,应用方便,利用不同循环周次对应的平均应变,即可方便地得出相应工况下的失效寿命和剩余寿命，非常适合用于实际工程的安全评估。

另一方面，如前所述，在相同的温度和加载条件下，材料表面及亚表面存在的夹杂物、缺陷等因素会导致材料的延性消耗快慢的不同，但对于材料延性本身没有影响，本文基于延性耗竭理论和损伤力学提出的寿命预测模型，对于相同温度和加载条件下出现寿命波动同样适用。图9为540 ℃时环境相同加载条件下，不同失效寿命的预测效果图，如前所述分别选取NF/4、NF/2、3NF/4附近对应的循环周次和平均应变采样点进行寿命预测,从图9可以看出,除个别异常点外，所有的数据点都位于1.5倍误差带以内,预测效果较好。

图9　540 ℃下疲劳-蠕变交互作用相同加载条件不同失效寿命的预测效果图

从上述试验结果可知，本文基于延性耗竭理论和损伤力学，利用材料延性的消耗来描述损伤，进而推导得到疲劳-蠕变交互作用寿命预测模型,对不同寿命段的采样数据均具有较好的预测效果，同时可以很好地解释以及预测相同温度和加载条件下出现的寿命波动，理论依据明确，形式简单，非常适合实际工程应用。

3　结论

(1)基于延性耗竭理论和损伤力学，对材料疲劳-蠕变交互作用下的延性消耗、损伤、循环周次和失效寿命之间的关系进行了分析，在此基础上，建立了一种疲劳-蠕变交互作用的寿命预测模型。模型形式简单，理论依据明确，可以很好地解释相同温度和加载条件下的寿命波动,同时可用于应力控制条件,非常便于实际工程应用。(2)用上述模型进行1.25Cr0.5Mo钢高温应力控制下疲劳-蠕变交互作用的寿命预测,对不同寿命段的采样数据均具有较好的预测效果,同时对相同温度和加载条件下出现的寿命波动情况也具有较好的预测效果。

[1]Miner M A.Cumulative Damage in Fatigue[J].J. Appl. Mech. Trans.,1945,67:A159-A165.

[2]Coffin L F.The Effect of Frequency on High-temperature Low-cycle Fatigue[C]//Proceedings of Air Force Conference on Fracture and Fatigue of Aircraft Structures and Materials.Miami:AFDL TR 70-144，1970:301-312.

[3]Coffin L F.The Concept of Frequency Separation in Life Prediction for Time-dependent Fatigue[C]//Symposium on Creep-fatigue Interaction.New York:ASME MPC-3,1976:349-363.

[4]Manson S S.Creep-fatigue Analysis by Strain-range Partitioning[C]//First Symposia on Design for Elevated Temperature Environment.New York:ASME,1971:12-28.

[5]何晋瑞.金属高温疲劳[M].北京:科学出版社,1988.[6]张国栋,赵彦芬,薛飞,等.P91钢蠕变-疲劳交互作用应变特征与寿命预测[J].中国电力,2011,44(10):54-59.

Zhang Guodong,Zhao Yanfen,Xue Fei,et al.Strain Performance and Life Prediction for P91 Steel under Creep-fatigue Interaction[J].Electric Power,2011,44(10):54-59.

[7]胡绪腾,马晓健,宋迎东.含保载弹性应力循环下TA12钛合金缺口试样的蠕变疲劳损伤分析[J].机械工程材料,2013,37(3):90-94.

Hu Xuteng,Ma Xiaojian,Song Yingdong.Creep-fatigue Damage Analysis of TA12 Titanium Alloy Notched Sample at Elastic Stress Cycle with Dwell Time[J].Materials for Mechanical Engineering,2013,37(3):90-94.

[8]胡绪腾,宋迎东.应用总应变-应变能区分法预测热机械疲劳寿命[J].燃气涡轮试验与研究,2012,25(1):14-16,53.

Hu Xuteng,Song Yindong.Life Prediction for Thermomechanical Fatigue Using Total Strain Version of Strain Energy Partitioning[J].Gas Turbine Experiment and Research,2012,25(1):14-16,53.

[9]陈学东,范志超,陈凌,等.三种疲劳蠕变交互作用寿命预测模型的比较及其应用[J].机械工程学报,2007,43(1):62-68.

Chen Xuedong,Fan Zhichao,Chen Ling,et al.Comparison among Three Fatigue-creep Interaction Life Prediction Models and Their Applications[J].Journal of Mechanical Engineering,2007,43(1):62-68.

[10]范志超,陈学东,陈凌,等.基于延性耗竭理论的疲劳蠕变寿命预测方法[J].金属学报,2006,42(4):415-420.

Fan Zhichao,Chen Xuedong,Chen Ling,et al.Prediction Method of Fatigue-creep Interaction Life Based on Ductility Exhaustion Theory[J].Acta Metallurgica Sinica,2006,42(4):415-420.

[11]董杰,陈学东,范志超,等.基于微裂纹扩展的疲劳蠕变寿命预测方法[J].金属学报,2008,44(10):1167-1170.

Dong Jie,Chen Xuedong,Fan Zhichao,et al.Prediction Method Of Fatigue Creep Life Based on Microcrack Propagation[J].Acta Metallurgica Sinica,2008,44(10):1167-1170.

[12]Goswami T.Creep-fatigue Life Prediction-a Ductility Model[J].High Temperature Materials and Processes,1995,14(2):101-114.

[13]Goswami T.New Creep-fatigue Life Prediction Model[J].High Temperature Materials and Processes,1996,15(1/2):91-96.[14]Goswami T.Low Cycle Fatigue Life Prediction-a New Model[J].International Journal of Fatigue,1997,19(2):109-115.

[15]沈为.损伤力学[M].武汉:华中理工大学出版社,1995.

[16]陈志平,蒋家羚,陈凌.1.25Cr0.5Mo钢疲劳-蠕变交互作用的损伤研究[J].金属学报,2007,43(6):637-642.

Chen Zhiping,Jiang Jialing,Chen Ling.Research on Fatigue-creep Interaction Damage of 1.25Cr0.5Mo Steel[J].Acta Metallurgica Sinica,2007,43(6):637-642.

[17]陈凌.典型压力容器用钢中高温环境低周疲劳和疲劳蠕变交互作用的行为及寿命评估技术研究[D].杭州:浙江大学,2007.

[18]中国国家标准化管理委员会.GB/T 15248-2008金属材料轴向等幅低循环疲劳试验方法[S].北京:中国标准出版社,2008.

(编辑王艳丽)

A Model of Life Prediction for Fatigue-creep Interaction and Its Experimental Verification

Chen LingZhang XianmingOuyang Ping

Engineering Research Center for Waste Oil Recovery Technology and Equipment of Ministry of Education,Chongqing Technology and Business University,Chongqing,400067

Based on the ductility exhaustion theory and damage mechanics, the correlation among the ductility consumption, damage, cycles and failure life of materials under fatigue-creep interaction was analyzed herein.And then, a model for fatigue-creep interaction life prediction was established.This model was very convenient for practical engineering applications because of its simple formation.Through fatigue-creep interaction experiments with smooth specimens of 1.25Cr0.5Mo steel at 540℃ and 520℃ under stress control, which used a trapezium waveform with the hold-time per cycle, the prediction of the failure life was carried out by this model. Compared with the experimental data, it is found that the predicted results are in good agreement with the experimental ones.Besides,this model can explain the life fluctuation under the same temperature and loading condition well.

fatigue-creep;ductility;damage;mean strain;life prediction

2014-06-16

国家自然科学基金资助项目(51375516);重庆市基础与前沿研究计划资助项目(CSTC2013jcyja50025);重庆工商大学科研启动经费资助项目(2014-56-10)

O346.2;TG115.5DOI：10.3969/j.issn.1004-132X.2015.10.014

陈凌,男,1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心高级工程师、博士。主要研究方向为金属材料的疲劳、断裂、腐蚀研究及机械结构安全评估。获发明专利9项。发表论文50余篇。张贤明,男,1955年生。重庆工商大学废油资源化技术与装备教育部工程研究中心教授。欧阳平，男，1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心副研究员。