基于耦合传热的涡轮增压器涡轮箱有限元分析

龚金科　田应华　黄张伟　贾国海

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于耦合传热的涡轮增压器涡轮箱有限元分析

龚金科田应华黄张伟贾国海

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于涡轮增压器涡轮箱传热机理，采用专业CFD软件和FEM软件分别建立了涡轮箱流体区域和固体区域网格仿真模型。在流体域建立多重旋转坐标系，精确计算出涡轮箱流场、壁面传热系数及温度。应用流固耦合的仿真方法对涡轮箱进行耦合传热分析，得到涡轮箱固体域的温度场并对其进行热应力分析。与实验结果对比发现，仿真模型的温度场符合实际涡轮箱温度分布，最大误差仅为3.3%。该涡轮箱耦合传热模型具有较高的精度，为涡轮增压器的设计优化提供了依据。

涡轮箱；耦合传热；温度场；热应力

0　引言

涡轮增压器安装在发动机的进排气歧管上,在高温、高压和高速运转的恶劣环境下工作，其各部件的温度分布不均匀[1-3]。随着涡轮增压技术的发展，涡轮增压器各零部件的工作环境越来越恶劣，涡轮箱等零部件的热负荷也逐渐增大，而涡轮箱的温度场和热应力状况很大程度上决定了涡轮增压器的可靠性[4]。长期以来,国内外涡轮增压器的研究多集中在涡轮叶片以及轴承体上，缺乏对涡轮箱流场、温度场和热疲劳的整体研究[5-7]。

本文基于涡轮箱传热机理，利用专业CFD软件和FEM软件对某发动机涡轮增压器涡轮箱进行耦合传热数值仿真研究，通过在流体区域建立多重旋转坐标系，模拟涡轮箱内腔废气的流动，得到涡轮高速旋转时涡轮箱流体域的流场、壁面传热系数和温度场分布，以及其固体域的温度场,分析了其热应力，并将仿真计算值与实验值进行了对比验证。

1　涡轮增压器涡轮箱传热原理

采用有限单元法对流体的流动与传热进行数值仿真，首先需要建立反映流体工程本质的数学模型。

高温废气在涡轮箱中的流动与传热过程都遵从质量守恒、动量守恒和能量守恒定律。

废气在涡流道内的流动属于湍流运动。简化的标准k-ε模型方程如下[8]。

湍流动能k方程：

(1)

式中，k为湍流动能；ui为湍流速度；μ为流体动力黏度；ρ为流体密度；μt为湍流动黏度;Gk为由平均速度梯度引起的湍流动能k的产生项；Sk为湍流动能源项;σk为湍流动能k对应的Prandtl数，σk=1.0;ε为湍流耗散率。

湍流耗散率ε方程：

(2)

式中,Sε为湍流耗散源项;σε为湍流动能耗散率ε对应的Prandtl数,σε=1.3;C1ε和C2ε为经验常数,C1ε=1.44,C2ε=1.92。

涡轮增压器涡轮箱的传热是一个非常复杂的传热过程,其内表面以对流和热传导的方式与高温废气进行换热的同时,又以热传导的方式向涡轮箱体进行传热。

在涡轮箱和高温气体接触的流固边界上,传热过程是一个涉及固体、流体和温度场等多个物理场同时作用的耦合传热过程。流固耦合是典型的弱耦合，只在边界上存在热量交换，其边界上的温度、传热系数都应看成是计算结果的一部分，而不是已知条件，在涡轮箱流固耦合传热边界上有[9]

qw|solid=qw|f luid

(3)

当黏性流体在贴近壁面附近流动且流速很小时,其相对运动可忽略不计。在涡轮箱废气与壁面交界处的固体一侧,由傅里叶导热定律可知[10]：

qw|solid=-λgradt

(4)

式中,λ为热导率;gradt为贴近壁面法线方向上流体温度变化率。

对流传热的牛顿冷却公式为[10]

qw|f luid=h(tw-tf)

(5)

式中,tw和tf分别为交界面和附近冷却液的温度;h为涡轮箱对流传热表面传热系数。

由式(4)、式(5)可以得到对流传热表面传热系数与流体温度场的关系式：

(6)

在采用数值法进行研究时，若只应用单一综合性有限元软件对正常工况下涡轮增压器涡轮箱进行数值模拟仿真计算,很难在减小计算量的同时保证较高的计算精度[9]。

本文采用ABAQUS软件提供的流固耦合传热交界面模型，如图1所示。在进行流固耦合传热仿真计算时，固体域和流体域之间可通过此交界面进行数据传递。当利用STAR-CCM+软件仿真计算出流体区域的壁面温度和传热系数后,将数据映射到图1所示的耦合传热交界面上,这将成为ABAQUS软件计算的第三类热边界条件。计算得到涡轮箱固体区域的温度场，再通过耦合传热交接面将固体区域内腔壁面温度映射到流体区域,这将成为流体软件STAR-CCM+计算的壁面温度条件。如此反复计算，直到涡轮箱体节点上的温度不再发生变化为止。得到精确的涡轮箱固体区域温度场分布后，将此温度场导入ABAQUS预定义场，并利用其力学模块计算涡轮箱热应力，其过程如图2所示。

图1　耦合传热交界面

图2　计算过程

2　涡轮增压器涡轮箱仿真模型

2.1涡轮增压器涡轮箱网格仿真模型

图3　涡轮箱固体区域网格模型

在进行数值仿真计算前，对涡轮箱外表面倒角和细小结构进行简化，可避免计算出错并使计算收敛更快。通过几何处理后采用四面体网格对涡轮箱划分体网格，图3为涡轮增压器涡轮箱固体区域网格模型，其节点数为69 230，网格数为312 358。建立涡轮箱流固耦合模型，还需对流体区域进行网格划分。为了精确模拟流体流动需要采用边界层网格，在进出口区域设置拉伸层网格，以保证流体流动的稳定性。运用几何编辑软件将导入的涡轮箱的外表面删除，提取内腔壁面，对进出口处进行封面处理，将其转换为实体并分割为三部分，即进口段、出口段以及涡轮旋转区域，如图4所示。

图4　流体区域网格模型

在进行流体计算时，为了更精确地模拟高温废气的流动，需建立交界面INTERFACE模型和多重旋转坐标系MRF模型：分别在涡轮旋转区域与流体进口段和出口段设置接触面INTERFACE1和INTERFACE2，用于不同区域之间的物质及能量传递；在涡轮旋转区域，建立MRF模型，并定义其旋转方向和转速，实现动网格的高速旋转。图4为涡轮箱流体区域网格模型，共有354 380个节点，1 327 725个单元。

2.2物理模型材料

准确的材料物性参数是仿真分析获得准确结果的重要前提。在ABAQUS软件中，对于固体域通常需要提供固体材料的热导率、质量热容、密度等参数。涡轮增压器涡轮箱的材料选用灰铸铁，其密度为7010 kg/m3，质量热容为510 J/(kg·K),泊松比为0.274,热导率为47W/(m·K),线膨胀系数为1.5×10-5K-1,弹性模量为160 GPa。

2.3边界条件

涡轮箱承受的热载荷与发动机气缸数、废气温度等密切相关，是一个随时间变化的交变载荷。本文在研究涡轮箱温度及热应力时，视高温废气的流动为三维不可压缩的黏性湍流流动，湍流模型采用k-ε湍流模型。入口采用质量流量边界条件，根据提供资料，选取涡轮转速为220 kr/min,使用GT-Power/Endenvironment模块建模,计算得到正常工况下废气温度T及质量流量qm随时间变化情况,并导入STAR-CCM+,成为流体计算的入口边界条件,如图5所示。

图5　增压器入口端废气质量流量及温度随时间变化

涡轮箱采用压力出口边界条件,由于涡轮叶片高速旋转导致气流在出口端产生湍动,故其出口压力p同样随时间变化,具体情况如图6所示。

图6　涡轮增压器出口端废气压力随时间变化

3　计算结果分析

3.1涡轮箱流场分析

通过流体计算得到涡轮箱内部废气压力以及速度分布。图7显示出了涡流道的压降过程，越靠近涡轮处，压降越明显。在涡轮叶片处，由于废气高速冲击涡轮，导致叶片与废气直接接触的一侧压力较高,而叶片的另一侧，压力最低，为0.116 40 MPa。图8为废气在涡流道内的速度矢量图，在入口端，速度最小且分布均匀。当废气进入涡流道后，由于流道的引流作用，废气速度增大，对比其压降云图，由于能量守恒，流道内废气的势能转换为动能,在达到涡轮叶片时呈现最高速度,为594.28 m/s,保证了涡轮获得动能最大。

图7　涡轮箱涡流道压力场分布

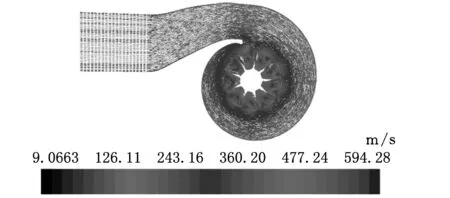
图8　涡轮箱涡流道速度场分布

3.2涡轮箱内壁面传热系数与温度分布

发动机废气具有很高的动能和势能，涡轮箱与之直接接触，会接收从废气中传出的大量能量。涡轮增压器涡轮箱内壁面的传热系数直接反映了高温废气和涡轮箱传热情况。

图9为流体计算得到的涡轮箱内壁面传热系数的分布云图，其传热系数处于569.07～4083.9 W/(m2·K)之间。从涡流道至出口端面,传热系数先减小后增大，显示出明显的传热系数梯度。最高传热系数分布在进口端涡流道与涡轮旋转区域交界面处，在此区域高温废气高速冲击涡轮叶片，并伴随着大量势能和动能之间的转换。整个涡流道由于在能量转换之前与高温废气充分接触，故此区域整体传热系数较大。

图9　涡轮箱内壁面传热系数分布图

传热系数直接影响温度的分布,如图10所示，可以看出涡轮箱内腔温度分布明显不均匀。总体从涡轮箱入口端至出口端呈现明显的下降趋势，高温区域分布在涡轮旋转区域，此区域由于剧烈传热导致局部温度较高，最高达到1185.7 K。进口涡流道总体温度较高，在1063.1 K以上,出口区域温度最低，仅为572.72 K。

图10　涡轮箱内壁面温度分布图

3.3涡轮增压器涡轮箱温度及热应力分析

涡轮箱在正常工作时，由于高温废气传热,故将其流体区域传热系数及温度映射到涡轮箱固体网格内腔壁面上，作为计算固体域温度场的第三类热边界条件。

在ABAQUS软件中进行计算,得到涡轮箱温度场分布情况，如图11所示，涡轮箱温度分布趋势总体上向出口端递减，这是由于涡轮箱主要的热源来自发动机排放的废气，高温废气通过涡轮箱流道时与之充分接触，热量迅速传递到涡流道壁面上，且废气大量势能转化为涡轮叶片的动能，越靠近出口端温度越低。涡轮箱整体温度较高，在624.2～1176 K之间。最高温度在进气涡道、进气法兰及V形圈边，都超过1130 K,最低温度分布在涡轮箱尾部出口端下缘,局部甚至温度不足700 K。涡轮箱入口端和出口端温差较大,从1176 K迅速降低到624 K。涡轮箱进气法兰端面温度分布不均匀,在900～1100 K之间,越靠近涡流道的区域温度越高。

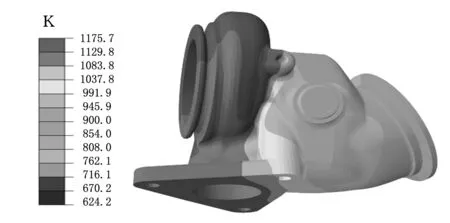
图11　涡轮箱整体温度分布

图12为涡轮箱热应力分布情况，涡流道入口、V形圈边等部位，热应力远大于其他部分热应力，涡轮箱有两边向中间挤压的变形趋势,这主要由于涡轮箱进出口端被安装固定，温度变化使得涡轮箱高温的部位产生膨胀，而这种膨胀受到法兰、阀门圈座等固定部位的限制，从而产生局部热应力。

图12　涡轮箱整体热应力分布

图13显示了涡轮箱流道截面温度分布情况，在正常工作状态下，涡流道长时间承受高温，其内壁面的温度达到最高，接近排气温度，涡轮箱流道整体温度在1100 K以上，在涡流道导向喷嘴处，其内外侧温差较大。

图13　涡轮箱涡流道截面温度分布

图14所示为涡轮箱涡流道截面热应力分布情况,当发动机冷却60 s后,内外侧受热状况不一样，涡流道外壁面迅速降温，内表面由于残气继续加热，温度下降较慢，导致温度梯度增大，故涡流道局部温度不均而产生热应力，越靠近固定法兰处热应力越大。涡流道导向喷嘴处由于壁厚较薄，在冷却过程中其内外侧温差较大,易产生较大热应力。设计时在保证能量转换效率下适当增加导向喷嘴厚度，可有效减小热应力。

图14　涡轮箱涡流道截面热应力分布

图15为涡轮箱整体截面的温度分布云图，从涡流道至出口端，温度下降较快，形成明显温度梯度。针对本模型的单流道涡轮箱，其入口端的涡流道温度较高，都处于1100 K以上,因此区域在高温、高压、高速的恶劣工况下工作并伴随大量能量的转换。涡轮箱整体涡流道部分温度分布不均匀，越靠近废气出口端的涡流道部位温度越低。

图15　涡轮箱截面温度分布

图16显示了涡轮箱截面热应力分布情况。对于入口端，停机冷却时，由于内部受到残余废气的继续加热，其温度较为稳定，而法兰的边缘温度下降较快，由于螺栓固定住了法兰面，导致法兰面高温区域膨胀受挤压，故产生热应力及变形。在法兰端螺栓孔处设置凸台，可减小螺栓孔热应力，同时在保证密封前提下采用弹性垫圈可缓解法兰端部分热应力。在V形圈边处可适当增加其厚度，并在保证密封前提下采用弹性垫圈，可缓解由于限制热膨胀而产生的热应力。

图16　涡轮箱截面热应力分布

4　实验验证

对于机械零部件而言，热应力产生的主要原因有两个方面：一方面是不同材料由于不同的热膨胀系数导致变形不均；另一方面是相同材料本身冷热不均致使热胀冷缩产生变形以及变形位移受到某些限制而导致。对于涡轮箱而言，箱体由相同材料构成，热膨胀系数的不同由温度差异造成，而这些差异不足以对热膨胀系数产生太大的影响，可以忽略，因而，涡轮箱热应力的主要来源是冷热不均。涡轮箱处于冷热交替变化的工作环境中，因而对其热应力的研究实际在很大程度上可以等价为对其温度场的研究[11]。基于本文中的涡轮增压器实验台架，对涡轮增压器涡轮箱的温度分布进行实验研究,能够为流固耦合数值模拟计算提供更准确的边界条件,同时也可以用于实验结果与数值模拟结果的对比分析。

在涡轮增压器涡轮箱的传热实验中，采用WRTK-112工业铠装热电偶分别对涡轮箱内外表面进行温度测量并验证模拟仿真的准确性[12]。由于测试条件的限制，部分测点的温度无法直接测量，需要进行间接测量，如本文的涡轮箱温度实验，常用的方法是在涡轮箱壁面上，从外部向内部开测量孔，测量孔直径为1 mm，测点底部安装热电偶球头，位置距离涡轮箱内壁面为0.5 mm,温度测量结果作为估算涡轮箱内壁面温度值参考。考虑零件工艺要求和安装的便捷性，温度测点布置如图17所示，其中测点1～6、10～12主要用于进行涡轮箱温度测量实验及结果分析；测点7～9、13～16采用间接测量的方式，在涡轮箱壁面上开测量孔，测量涡轮箱内壁面的温度，主要用于进行传热边界测量实验。

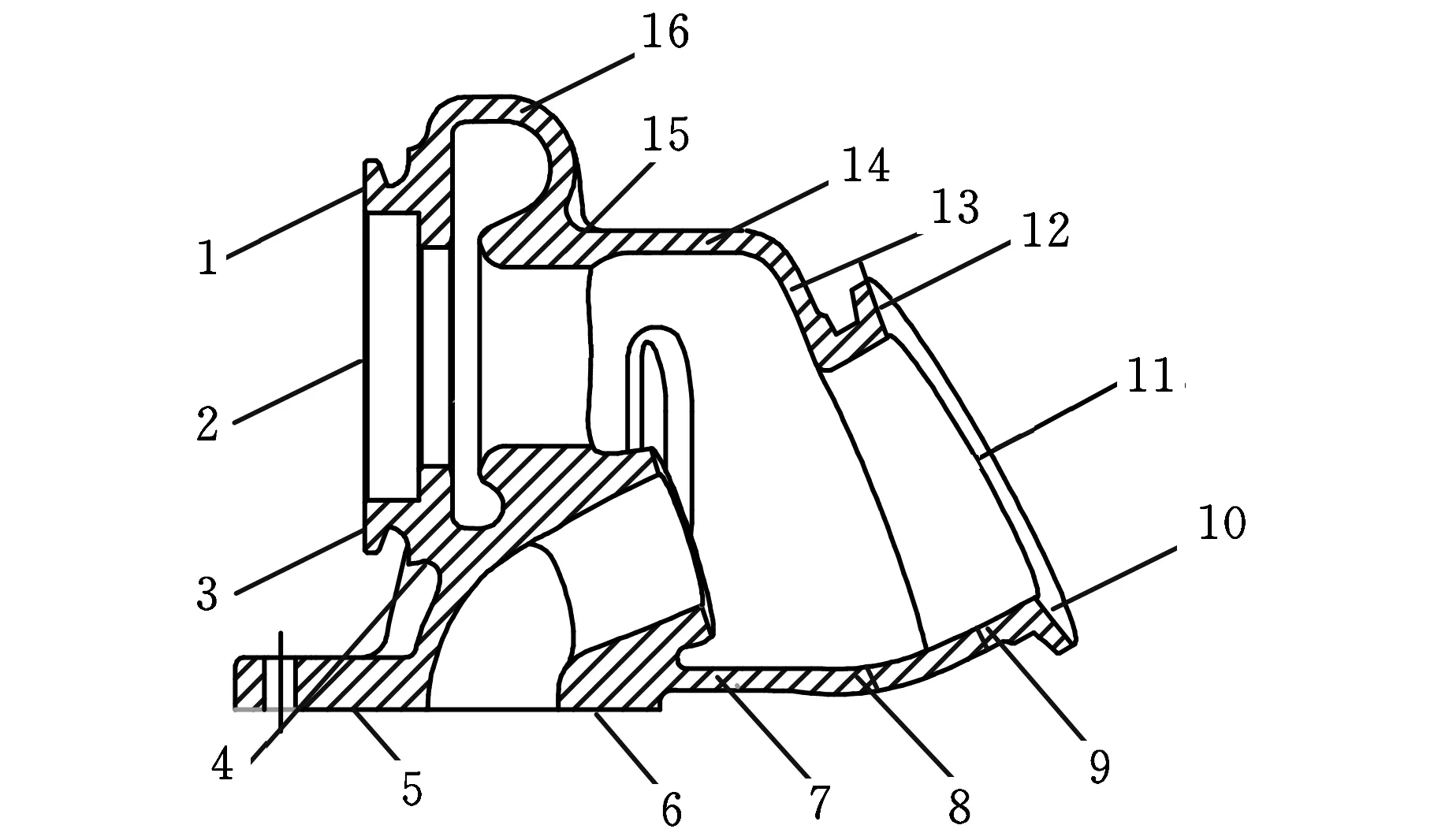
图17　涡轮箱测温点分布

流固耦合传热边界实验在实验台架稳态运行工况下进行，使用燃烧时加热后排出的气体模拟发动机废气驱动涡轮增压器，在涡轮增压器稳定运行20 min后读取各测点温度值(图18)。测量实验测点温度与数值模拟实验结果对比如表1所示,各测点计算温度值与实测值最大误差仅为3.3%。即经过实验验证，利用流固耦合数值模拟的方法对涡轮增压器涡轮箱内气体流动及传热分析是准确及可靠的。

图18　实验设备

测点编号实测值(K)计算值(K)误差(%)测点编号实测值(K)计算值(K)误差(%)11152.11137.31.39822.4819.10.421119.91126.7-0.610812.8800.41.531162.51130.82.811895.9914.22.041104.61127.1-2.012979.8967.21.351143.41126.51.513929.8960.7-3.361083.41066.31.6141025.21056.9-3.071014.4991.62.3151051.31078.7-2.68888.9898.8-1.8161113.41138.7-2.2

5　结论

(1)基于MRF模型对涡轮箱进行流体计算，得到流体域的流场、壁面传热系数及温度分布情况。计算结果表明，废气的势能和动能在涡轮处转化最剧烈；从涡流道至出口端，传热系数先减小后增大，显示出明显的传热系数梯度，最大传热系数分布在流固耦合交界面处，其次是涡流道区域；传热系数直接影响涡轮箱的温度分布，温度总体上呈现从进口端向出口端递减趋势，在涡轮箱出口端温度最低。

(2)涡轮箱整体温度较高使得高温的部位产生膨胀，各部位由于温度不均使膨胀程度不一致，且受到法兰等固定部位的限制，从而产生局部热应力。其中进气法兰端面、涡流道以及导向喷嘴等处热应力最大，应在设计时进行优化。

(3)通过测量实验测点温度并与数值模拟实验结果进行对比，可知数值模拟结果非常接近实验值，验证了利用流固耦合数值模拟对涡轮增压器涡轮箱内废气流动及传热分析的方法准确性和可靠性。

[1]张俊红,李志刚,王铁宁,等.车用涡轮增压技术的发展回顾、现状及展望[J].小型内燃机与摩托车，2007，36(1):66-69.Zhang Junhong,Li Zhigang,Wang Tiening,et al.The Past,Present and Prospects of the Development on Vehicle Turbo Technology[J].Small Internal Combustion Engines and Motorcycles，2007(1):66-69.[2]周虹伟.涡轮增压器主要部件结构特性及改进研究[J].中国铁道科学,2004,25(2):72-77.

Zhou Hongwei.The Structure Characteristics and Improvement of Main Components of Turbo-supercharger[J].China Railway Science，2004,25(2):72-77.

[3]李志江.柴油机废气涡轮增压器的常见故障与使用保养[J].工程机械与维修,2008(4):198-199.

Li Zhijiang.The Common Fault and User Maintenance on Diesel Exhaust Turbocharger[J].Construction Machinery & Maintenance,2008(4):198-199.

[4]廖爱华.增压器的非线性力学分析[D].大连:大连理工大学,2007.

[5]胡友安,李晓东,陈图钧,等.涡壳温度场和热应力的有限元分析[J].机械强度,2007,29(1):130-134.Hu Youan,Li Xiaodong,Chen Tujun,et al.Analysis on Temperature Field and Thermal Stress of Turbocharger Housing by Finite Element Method[J].Journal of Mechanical Strength,2007,29(1):130-134.[6]Errera M P, Chemin S. Optimal Solutions of NumericalInterface Conditions in Fluid-structure Thermal Analysis[J].Journal of Computational Physics,2013,245:431-455.

[7]Pesiridis A,Martinez-botas R F.Experimental Evaluation of Active Flow Control Mixed-flow Turbine for Automotive Turbocharger Application[J].Journal of Turbo Machinery,2007,129(1):44-52.

[8]徐行军.柴油机冷却系统结构优化及缸盖热应力分析[D].天津:天津工业大学,2010.

[9]傅松,胡玉平,李新才,等.柴油机缸盖水腔流动与沸腾传热的流固耦合数值模拟[J].农业机械学报,2010,41(4):26-30.

Fu Song,Hu Ping,Li Xincai,et al.Chamber Cylinder Head Water Flow and Heat Transfer Simulation Boiling Fluid-structure Interaction[J].Agricultural Machinery,2010,41(4):26-30.

[10]贾力,方肇洪. 高等传热学[M]. 北京:高等教育出版社,2008.

[11]胡友安,李晓东.涡轮增压器蜗壳热裂纹的试验研究[J].河海大学学报,2008,36(6):846-849.

Hu Youan,Li Xiaodong.Experimental Study on Heat Cracks of Turbine Housing on Turbochargers[J].Journal of Hehai University,2008,36(6):846-849.

[12]徐思友,吴新涛,闫瑞乾,等.增压器轴承和密封环温度试验研究[J].车用发动机,2010(2):35-37.

Xu Siyou,Wu Xintao,Yan Ruiqian,et al.Experimental Study on Temperature for Turbocharger Bearing and Sealing Ring[J].Vehicle Engine,2010(2):35-37.

(编辑王艳丽)

Finite Element Analysis on Turbocharger Turbine Box Based on Coupled Heat Transfer

Gong JinkeTian YinghuaHuang ZhangweiJia Guohai

State Key Laboratory of Advanced Design and Manufacture for Vehicle Body of Hunan University,Changsha,410082

Based on the heat transfer mechanism of the turbocharger turbine box,a fluid mesh model and a solid one for simulation were built by using the professional software CFD and FEM respectively.The multiple coordinate system of rotation in the fluid domain was established to calculate accurately the flow field of turbine boxes,heat transfer coefficient and temperature.Coupled heat transfer analysis of the turbocharger turbine box was carried out by the fluid-solid coupling method,and then the temperature field for solid areas was obtained.Based on the temperature,its thermal stress analysis was carried out. In comparison with the experiments,the temperature distribution of the simulation model accords with that of the realistic turbocharger turbine box, the maximum deviation is only 3.3%.The coupled heat transfer model for the turbocharger turbine box has a high accuracy,which provides the basis for better design of turbocharger turbine.

turbine box;coupled heat transfer;temperature field;thermal stress

2014-07-04

国家高技术研究发展计划(863计划)资助项目(2008AA11A116);汽车车身先进设计制造国家重点实验室自主课题资助项目(61075002);湖南省自然科学基金资助项目(10JJ6080)

TK411.8DOI：10.3969/j.issn.1004-132X.2015.10.012

龚金科,男,1954年生。湖南大学机械与运载工程学院教授、博士研究生导师。主要研究方向为汽车排放及控制技术，热动力设备新技术等。田应华，男，1988年生。湖南大学机械与运载工程学院硕士研究生。黄张伟，男，1986年生。湖南大学机械与运载工程学院硕士研究生。贾国海，男，1986年生。湖南大学机械与运载工程学院博士研究生。