基于近似动态规划的动态车辆调度算法
李 雪 聂兰顺 齐文艳 战德臣
哈尔滨工业大学,哈尔滨,150001
基于近似动态规划的动态车辆调度算法
李雪聂兰顺齐文艳战德臣
哈尔滨工业大学,哈尔滨,150001
针对物流配送服务业中,车辆调度问题日渐呈现任务规模大,车辆类型多、属性多,调度实时性要求越来越高等特点,提出了基于近似动态规划的动态车辆调度算法。根据当前的任务需求与车辆状态以及相应的约束条件作出相应的调度,并且对一些样本进行训练,得到了一个近似价值函数。通过该价值函数,即可对任务迅速作出相应的决策。仿真模拟实验证明了该算法的有效性和优越性。
服务资源;近似动态规划;动态调度;价值函数
0 引言
针对车辆动态调度问题,国内外专家学者开展了一系列研究。Gendreau等[1]着重研究了车辆动态调度问题中出现的各种不确定性信息的影响,指出在求解此问题时,对这些不确定性信息应加以全面考虑;Powell[2]详细分析了车辆动态调度问题中一类随机车辆调度模型,采用改进的A-priori两阶段优化方法求解了该问题;Minkoff[3]以马尔可夫决策模型为基础,完成了车辆动态调度问题基于马尔可夫决策过程的建模求解,研究提出的算法在中小规模(10个需求)的车辆动态调度问题求解中可以得到比较满意的解,但因其模型的局限性,算法对大规模的问题难以求解。针对动态车辆调度问题实时性强的特点,张景玲等[4]、王旭等[5]研究了车辆的动态调度问题,通过基于两阶段优化的方法对该类问题进行了有效求解。袁建清[6]以解决车辆利用效率最大化为目标,建立了几类随机数学模型,提出了相应的智能算法,解决了车辆调度的不确定调度问题。文献[7-9]针对车辆动态调度中的不同问题提出了相应的解决方法。
本文以军事行动中车辆动态调度问题为背景,提出了基于近似动态规划的车辆动态调度算法。通过对车辆调度问题进行形式化描述,利用近似动态规划方法对车辆动态调度问题进行建模,根据近似动态规划的思想,设计实现求解大规模、多类型车辆调度的算法,并对算法进行了仿真性实验,验证了算法的有效性和优越性。
1 动态车辆调度的问题
车辆调度问题对实时性有较高要求,即在尽可能短的时间内,通过合理的运输方式、运输路径、运输工具组合来完成调度任务,是动态车辆调度问题领域关注的重点。对于动态车辆调度问题,本文以一个有关的军事任务中的车辆调度情景予以描述,如图1所示。

图1 军演中车辆调度情景图
在某次军事演习中,共涉及有1个车辆调度中心和N个驻防要点,车辆调度中心拥有载重车、乘坐车、牵引车和特种车四种类型的运力资源,共K辆运输工具。每个驻防要点拥有兵员、物资、装备等参演要素。演习中,需要在这N个驻防要点之间完成兵员、物资和装备的调运服务。演习过程中无法预知哪个驻防要点具有运输任务请求。根据描述情况,可对上述场景进行抽象,得到如表1所示的信息。

表1 大规模、多类型动态车辆调度问题范围约束
将本文研究的问题看作一个系统,问题中每个时刻的调度场景就可看作是该系统的一个状态,那么每个时刻的系统状态与该时刻的调度决策是一一对应的,不同的调度决策导致系统到达不同的状态,因此,每个时刻不同的系统状态价值,可以反映不同调度决策的优劣。由此,文中系统状态价值的含义可以描述为:每个时刻不同的调度决策会对系统的现状和将来产生不同的贡献,由此,每个时刻的系统状态价值就是该时刻对应调度决策对系统的贡献值。
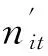
由此,我们用系统状态价值来定义本文研究问题的优化目标:根据每个时刻不断出现的运输任务请求和不断变化更新的车辆状态,在一定条件下(如运输任务类型、任务起止时间、车辆剩余载重、单次最大行驶里程等),动态查询所有车辆状态,挑选合适的车辆,规划合理的路线,尽可能地满足任务点的运输任务请求,使得每个时刻的系统状态价值最大。
2 动态车辆调度问题模型
根据上述情景分析,对此调度场景建立相应的模型,主要包括车辆资源、任务信息和调度决策等。
2.1车辆资源
车辆资源建模的基本思想是抽象出车辆资源的重要属性,明确车辆资源的使用规则,从而约束车辆属性向量的空间取值。车辆属性主要包括静态属性和动态属性:静态属性描述车辆资源的基本特点;动态属性刻画车辆资源的状态。

通过以上对车辆资源的建模,可以得到:t时刻,可以调度的具有属性a的车辆资源的数量为
t时刻,可以调度的车辆资源的数量为
Rt=(Rta)a∈A
2.2任务信息
任务请求信息也可以看作是系统资源,为了刻画运输任务的多方面属性以及运输任务的静态属性和动态属性,笔者建立了调度决策模型。通过属性向量来描述和刻画运输任务的状态;通过明确运输任务的使用规则,来约束其属性向量的空间取值。

那么,t时刻需要被满足的、具有属性b的运输任务请求的数量为
t时刻需要被满足的任务数量为
Mt=(Mtb)b∈B
2.3调度决策
调度决策属于动态系统的内部信息,为了刻画调度决策的内容以及调度决策如何起效作用于车辆资源和运输任务,对调度决策的建模要从对车辆资源和运输任务的状态影响出发,抽象其重要属性,通过定义调度决策的策略集,来约束其属性向量的空间取值。
d为调度决策的属性向量,d=(d1(当前派遣),d2(暂不派遣),d3(执行车辆编号),d4(执行任务编号),d5(预派遣时刻));Da为可以作用于具有属性a的车辆资源向量;Π为可行调度策略的集合。调度策略是指在给定系统状态信息的前提下,决定一个调度决策的规则。在本文的研究中,调度策略由贡献函数(反映当前调度决策对系统当前贡献的影响)和近似价值函数(反映当前调度决策对系统未来的影响)共同来反映。xtad为t时刻,具有属性a的,被决策d作用的车辆的数量,则

(1)
xtad≥0,∀a∈A,d∈Da
σtad为决策结果指示函数,用来捕获决策的结果,且
那么t时刻,被派遣执行运输任务的、具有属性a的车辆数量为σtadxtad;χt为t时刻,在给定有效信息下的可行调度策略的集合。
为了通过数学形式来反映决策结果,需要定义一个决策函数,一些调度策略,在每个取样时刻,给定系统的状态信息,返回调度决策。

(2)

本文在车辆调度决策过程中,考虑了两种车辆调度方式:一是单车多任务,二是多车单任务。
此外,为了计算的方便,对时间采取离散时间模型,如图2所示。在前述的对车辆资源、运输任务、调度决策的符号中,右下角的时间角标“t”,表示的是离散时间点t时刻或第t期,第t期指t=(t-1,t]。

图2 取样时刻模型
2.4目标方程
把大规模、多类型车辆动态调度问题看作是一个“动态系统”,把每次作调度决策的场景看作是该系统在时间轴上的一个“状态”St。St由车辆资源状态Rt-1、运输任务信息Mt和调度决策xt共同描述。St的价值是由贡献函数和近似价值函数共同决定。贡献函数捕获调度决策xt对当前系统状态的影响;近似价值函数捕获调度决策xt对未来系统状态的影响。本文优化目标为:“每期决策,使得在尽可能完成运输任务的前提下,动用的车辆数最少;长期目标是在完成尽可能多的任务前提下,车辆动用率最低。”,那么,大规模、多类型车辆动态调度问题的目标方程可以形式化表达为
(3)

当然,式(3)还要满足一定的约束条件:①调度决策作用的车辆资源数量不能超过当前已知的可调度车辆资源的数量;②每个时刻的调度决策满足的任务请求数不能超过当期已知的任务请求数;③调度决策作用的车辆资源数量、运输任务数量都是正整数。
3 基于近似动态规划的动态车辆调度方法
动态规划是基于多阶段决策过程寻优问题提出的,广泛应用于工程学、运筹学、经济学等多个领域[10]。但是,经典动态规划所面临的“维数灾难”使其只能解决小规模问题,限制了其应用[11]。通过上面的建模,本文采用近似动态规划(ADP)的思想设计动态车辆调度算法。
3.1基本思路和设计流程
基于ADP方法求解大规模、多类型的车辆动态调度问题需要划分为两个阶段,第一阶段是训练获取近似价值函数的表达式,第二阶段是应用训练得到的近似价值函数的表达式指导车辆调度。ADP在训练数据阶段是用本次系统产生的数据去更新上一次假设的数据,即将来对过去的影响,不断地更新进而产生出近似价值函数;在应用阶段就是利用训练阶段产生的近似价值函数来生成任务到来时的决策,即对未来的影响。
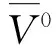
因此,第一阶段算法的输入是仿真得到的任务信息,输出为训练周期中每期系统状态价值的近似值。通过仿真任务信息来获得、辨识和测量训练阶段算法的各种参数,比如折扣因子、步长以及系统状态初值等。在第二阶段,应用第一阶段训练得到的近似价值函数表达式,根据当前的运输任务信息,求解决策函数(式(2))以得到优化调度决策xt。因此,第二阶段算法的输入为当前运输任务信息,算法的输出为优化的调度决策xt。
3.2调度策略的启发式规则
在求解大规模、多类型车辆动态调度问题中,本文中车辆调度策略的启发式算法规则集如下:
(1)对于每期出现的新运输任务,尽量从已经派出在外执行任务的车辆中挑选满足新运输任务要求的车辆,而尽量避免从调度中心增派车辆去满足新任务,以此来减少每期的车辆动用数量。
(2)对于当期出现的多个运输任务,按照任务开始时间的紧急程度,优先满足任务开始时间早的任务。
(3)对于在当期随机出现的运输任务请求,在任务开始时间和任务量满足的前提下,优先考虑与现有任务是否可以合并执行,以减少车辆动用的数量。
(4)对于可以满足某一运输任务的多辆可调度车辆,先将这些车辆按照剩余载重的大小进行排序,然后依次挑选剩余载重大的车辆去执行该运输任务;对于剩余载重也相同的车辆,按照可以到达任务起始点的时间排序,依次选择可以最早到达任务起始点的车辆执行该运输任务,这样可以在多车单任务中,减少车辆动用的数量,从而降低车辆的动用率。
启发式规则的输入为当前时刻的运输任务信息,即需要被满足、具有某属性的多个运输任务;输出为可调度的车辆序列和已调度的车辆序列。算法具体步骤描述如下。
(1)查询当期任务信息Mt,按任务类型分类汇总得到每种类型任务数量Mt b2。
(2)对于当期出现的每个任务Mt b,按当期任务的开始时刻从小(早)到大(晚)排序。
(3)for当期出现的、开始时间最早的任务:
do按任务类型要求、开始时间要求查询是否有在外执行任务的、可调度的相应类型的车辆资源状态。
if有在外执行任务的、可调度的车辆,
do返回在外执行任务的、可调度的车辆资源序列。
else查询在调度中心的车辆资源,返回可调度的车辆资源序列:
Rt,a2=1,a3≠0Rt,a2=2,a3≠0Rt,a2=3,a3≠0Rt,a2=4,a3≠0
(4)将步骤(3)中得到的可调度车辆按剩余载重/员从大到小进行排序,得到每种类型可调度的车辆序列:
Rt,a2=1,a5Rt,a2=2,a5Rt,a2=3,a5Rt,a2=4,a5
(5)对步骤(4)中挑选出来的可调度车辆序列中,再对剩余载重相同的车辆按照起效时间从小(早)到大(晚)进行排序,得到每种类型可调度的车辆新序列如下:
Rt,a2=1,a5,a10Rt,a2=2,a5,a10Rt,a2=3,a5,a10Rt,a2=4,a5,a10
(6)计算单车是否可以满足该任务。
if单车满足,do转至步骤(7),else转至步骤(8)。
(7)从步骤(5)中挑选第一辆车。
(8)从步骤(3)中依次挑选车辆,直到车辆组合剩余载重之和满足任务量要求。
(9)按照贡献函数的定义式计算不同调度决策的贡献值,按当前最大贡献值对应的调度决策调度车辆执行任务。
(10)将当期没有车辆满足的任务顺延至下一期转至步骤(1)。
3.3采用价值迭代和平滑策略训练近似价值函数的算法设计
大规模、多类型车辆调度问题训练阶段的算法采用价值迭代和平滑策略来获取系统状态的真实值。具体算法步骤如下:
(1)初始化。
②设置n=1,N=100,n为取样路径标记,N为总的取样次数;
(3)对于训练阶段的每一个取样时刻,t=1,2,…,30。

②调用前述的启发式规则算法,筛选得到最优的执行车辆;
③将执行车辆中可以推迟派遣的,推迟一期派遣;
⑤更新价值函数:
(4)
⑥计算车辆资源状态转换函数,更新车辆资源状态:
(4)n加1,如果n≤N,跳转至步骤(2)。
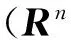
接下来可计算近似价值函数的线性表达式:
其中,θ1、θ2和θ3为待定参数,根据上述ADP求解问题的算法步骤(5)达到稳态的一组有效值,采用线性回归的方法求解得到待定参数θ1、θ2和θ3,从而得到近似价值函数的线性表达式。
3.4应用近似值函数进行大规模、多类型车辆调度算法设计
大规模、多类型车辆动态调度问题应用阶段算法是对训练阶段获得的近似价值函数进行调度应用,具体算法步骤如下:
(1)初始化车辆资源的状态R0。
(2)输入当前时刻的运输任务信息Mt。
(3)调用前述的启发式规则算法,求解决策函数:
(5)
其中,调度决策xt为式(5)的解。
(4)更新车辆资源状态:
Rt=RM(Rt-1,ωt,xt)
4 实验
4.1实验场景以及训练结果
根据上文中算法的描述,进行了相应的实验。实验过程中,假定有4种不同类型的车辆,每种类型的车辆有10辆,10个任务点,4种不同的任务。价值迭代算法需要为其设计合理的收敛准则。实验中,在取样时间轴上,具有相同周期长度和固定期数的一组连续的系统状态,本文尝试分别取样50次和取样100次,观察每条取样路径上某一相同时刻系统状态价值的近似值是否趋于稳态,用MATLAB分析,结果如图3所示。

(a)每条取样路径上 t1时刻的系统状态近似值(50次)

(b)每条取样路径上 t1时刻的系统状态近似值(100次)图3 算法迭代50次和100次后系统近似值变化图
由图3观察比较可以发现:算法在迭代50次后系统状态近似值依然呈现出稳步上升趋势,说明值迭代策略还未逼近到系统状态的真实值;在迭代100次后,观察发现系统状态近似值已经趋于稳态,说明值迭代策略已经逼近到系统状态的真实值,算法已经收敛,所以算法可以终止。
取第100次迭代的最后一组系统状态近似值进行拟合求解,求得近似价值函数的线性表达式,如表2所示。

表2 选取第100次取样的系统状态的
由此得到近似价值函数的线性表达式如下:
(6)
这里采用粒度比较大的线性拟合方式,拟合前这组系统状态近似值的空间表现形式和拟合后近似价值函数的空间展现形式分别如图4和图5所示,由于线性函数存在的误差较大,因此本文用尽可能多的离散值,用非线性的表达方式来得出这个函数。

图4 拟合前达到稳态的系统状态近似值空间分布

图5 拟合后近似价值函数的空间形式
图4、图5中,z轴为当期系统系统状态近似值,x轴为当期车辆动用数量,y轴为当期任务满足数量,由图可见近似价值函数的线性表达式能够比较好地匹配解空间的值。
4.2算法正确性验证
得到了近似价值函数的表达式之后,我们首先进行算法正确性的验证。利用单期决策(忽略一期以后的影响)的满意度“D”来反映算法的正确性,决策满意度的计算如下:
D≈N1/N2
(7)
其中,N1表示当期应该被满足的运输请求任务数,N2表示应用近似价值函数计算后得到的当期实际被满足的任务数。决策满意度越高,说明算法越正确。
通过近似价值函数的表达式(式(6))求解决策函数(式(1)),得到的调度决策结果为x1ad=5,x2ad=1,即1时刻的任务全部派遣车辆执行,2时刻的任务执行任务6。
算法正确性分析:最优的调度决策为1时刻和2时刻的7个任务应该全部执行,即N1=7,而近似价值函数求解决策函数给出的调度决策是实际执行6个任务,即N2=6。如果下一时刻还能满足条件的话,会延期调度剩余的任务。
决策满意度由式(7)计算为85.71%,即正确性为85.71%。可见,算法能够在较短时间内,得到正确性较高的近似满意解。
4.3算法优越性验证
为了进行算法的优越性验证,首先从算法的策略角度进行分析。基于ADP的大规模、多类型车辆动态调度算法的优越性,主要体现在算法在每期的调度决策中不但都考虑了当期决策对当期系统状态的影响,还考虑了当期决策对系统未来各期的影响。由此,如果我们仅以基于ADP算法中的启发式规则集为基础,只考虑当期决策对当前系统贡献值的影响而不考虑对将来各期的影响,设计一个大规模、多类型车辆动态调度的贪心算法,贪心算法实现就是任务到达只要有车辆满足条件就立即调度,这样就可以比较出两种调度策略的差异,从而判断哪种调度策略更为优越。
为了评判两种调度策略的优劣,我们根据问题的目标函数定义如下评判指标:
(8)
其中,R为目标值,N(t)为每期被满足的任务数,N(v)为每期调度动用的车辆数。对于本文的问题,我们的优化目标是:对于每期调度决策,在尽可能完成任务的前提下,动用车辆数最少。那么,式(8)中的目标值越大,则表明每期执行相同任务数的前提下,车辆动用的数量越少。
对两种算法给定同一组算例参数:取样次数N为100,训练周期T为30,每期任务数为1~15的随机数。
经过运行后,两种算法的各期目标值的平均值的整体图和局部图分别如图6和图7所示。

(a)基于启发式的ADP算法
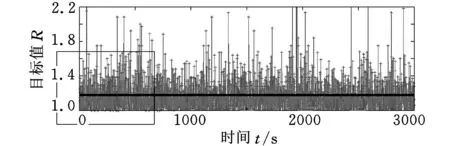
(b)基于启发式的贪心算法图6 两种算法的目标值比较(整体图)
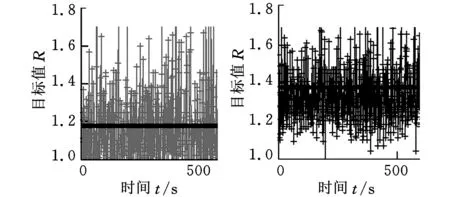
(a)图6a放大图(b)图6b放大图图7 两种算法的目标比较(局部放大图)
由图6和图7可见,基于ADP的算法策略目标值的平均值在1.4左右,而贪心算法目标值的平均值在1.2左右,这表明,按照ADP算法策略进行车辆调度,任务完成数量与车辆动用数量比值的平均值要比按照贪心算法策略高16.7%,即对于同样的任务,按ADP的调度策略进行车辆调度比按照贪心策略调度进行车辆调度,平均每期的车辆动用数量要少16.7%。这说明,既考虑每期调度决策的当期贡献值,又考虑对未来各期影响的ADP策略,要比只考虑当期贡献值的贪心策略优越,从而验证了算法的优越性。
5 结语
车辆调度问题因其规模大、类型多、不确定性强等特征需要动态的调度模型与调度优化算法。针对大规模、多类型车辆动态调度问题,基于近似动态规划的思想建立了系统状态模型和调度决策模型,提出了车辆动态调度的一系列启发式规则,在此基础上,提出了基于ADP的车辆动态调度训练算法和应用算法。基于训练算法所获得的仿真数据和属性聚集获得了系统的近似价值函数,基于该近似价值函数在应用阶段能够在线快速生成调度决策,为实际决策提供依据。实验结果表明,近似价值函数能够形成对状态价值的有效近似,算法(在缺少未来信息的前提下)所生成的调度能够兼顾当前和未来,显著好于贪心算法。因此,所提出模型和方法是解决大规模、多类型、不确定车辆动态调度问题的有效思路。实际应用过程中,其效果受模型的质量、参数的辨识准确性、训练数据的可获得性及准确性、对系统状态演化的实时跟踪能力等影响,需要针对真实系统进行适应性的调整、仿真和近似。
[1]GendreauM,PotvinJY.DynamicVehicleRoutingandDispatching[J].FleetManagementandLogistics,1998:115-126.
[2]PowellWB.StochasticandDynamicNetworksandRouting[J].DepartmentofCivilEngineeringandOperationsResearch,PrograminStatistics&OperationsResearch, 1995,8:141-295.
[3]MinkoffAS.AMarkovDecisionModelandDecompositionHeuristicforDynamicVehicleDispatching[J].OperationsResearch, 1993,41:77-90.
[4]张景玲,赵燕伟,王海燕,等. 多车型动态需求车辆路径问题建模及优化[J].计算机集成制造系统,2010,16(3):544-550.
ZhangJingling,ZhaoYanwei,WangHaiyan,etal.ModelingandAlgorithmsforaDynamicMulti-vehicleRoutingProblemwithCustomers’DynamicRequests[J].ComputerIntegratedManufacturingSystems, 2010,16(3):544-550.
[5]王旭,葛显龙,代应. 多车型动态需求车辆路径问题建模及优化[J].控制与决策,2012,27(2):175-181.
WangXu,GeXianlong,DaiYing,ResearchonDynamicVehicleRoutingProblemBasedonTwo-phasedAlgorithm[J].ControlandDecision, 2012,27(2):175-181.[6]袁建清.基于TS的动态车辆调度问题的混合算法研究[J].计算机现代化,2012(6):73-75.
Yuan Jianqing.Mixed Tabu Search Algorithm for Dynamic Vehivle Scheduling Problem[J].Jisuanji Yu Xiandaihua, 2012(6):73-75.
[7]Azi N, Gendreau M, Potvin J Y. A Dynamic Vehicle Routing Problem with Multiple Delivery Routes[J]. Annals of Operations Research, 2012, 199(1): 103-112.
[8]Warren B. Powell,Approximate Dynamic Programming for Operations Research[M]. Princeton:Department of Operations Research and Financial Engineering Princeton University, 2005.
[9]Clara Novoa,Robert Storer.An Approximate Dynamic Programming Approach for the Vehicle Routing Problem with Stochastic Demands[J]. European Journal of Operational Research,2009,196(2):509-515.
[10]Si J,Barot A G,Powell W B,et al.Handbook of Learning and Approximate Dynamic Programming: Sealing up to the Real World[M]. New York: IEEE Press and John Wiley & Sons,2004.
[11]Kirk D E. Optimal Control Theory: An Introduction[M]. Englewood Cliffs:Prentice_Hall,1970.
(编辑王艳丽)
An Algorithm of Dynamic Vehicle Scheduling Problem Based on Approximate Dynamic Programming
Li XueNie LanshunQi WenyanZhan Dechen
Harbin Institute of Technology,Harbin,150001
Vehicle scheduling in service industry of logistics distribution was presenting features including the tasks tended to be of large scale, vehicles were multi-type and had multiple attributes as well as high demands for real-time scheduling. To solve these problems, this paper proposed a dynamic vehicle scheduling algorithm based on the approximate dynamic programming. An approximate value function was obtained through training of some samples, and according to mission requirements, vehicle state and conditions, and quick scheduling decisions could be made with the value function. The simulation test has proved the correctness and effectiveness of the algorithm.
service resource; approximate dynamic programming; dynamic scheduling; value function
2013-04-23
国家自然科学基金资助项目(61273038);国家科技支撑计划资助项目(2013BAH17F03);国家重点基础研究发展计划(973计划)资助项目(2010CB328004);山东省自主创新成果转化重大专项(2012ZH1A0411)
TP311.52< class="emphasis_italic">DOI
:10.3969/j.issn.1004-132X.2015.05.020
李雪,女,1989年生。哈尔滨工业大学计算机科学与技术学院硕士研究生。主要研究方向为信息物理系统、资源动态调度。聂兰顺,男,1979年生。哈尔滨工业大学计算机科学与技术学院副教授。齐文艳,女,1987年生。哈尔滨工业大学计算机科学与技术学院硕士研究生。战德臣,男,1965年生。哈尔滨工业大学计算机科学与技术学院教授、博士研究生导师。

