前端调速式风力机组传动链建模与仿真

李仁年　刘　鑫　刘姝君

1.兰州理工大学,兰州,730050　　2.甘肃省风力机工程技术研究中心,兰州,730050

前端调速式风力机组传动链建模与仿真

李仁年1,2刘鑫1,2刘姝君1,2

1.兰州理工大学,兰州,7300502.甘肃省风力机工程技术研究中心,兰州,730050

对前端调速式风力机传动链关键部件的工作原理进行分析，建立数学模型。分别建立风速模型、风轮空气动力学模型、传动链动力学模型、液力变矩器动态模型以及主轴转速计算模型。整合各子系统，引入神经网络控制，建立传动链整体仿真模型，进行模拟仿真。基于最大风能捕获量,综合考虑传动链结构参数,通过神经网络调节液力变矩器导叶开度,改变工作油循环流量,从而改变液力变矩器的输出转矩和转速。液力变矩器输出与风轮输出通过行星轮系综合作用于发电机前的主轴，使主轴转速稳定在设计值。

风力机;传动链;液力变矩器;建模与仿真

0　引言

为了最大限度地捕获风能,风力机一般采取风轮变转速运行，以适应风速的变化。这与同步发电机并网发电时需要主轴定转速运行产生了矛盾。为了满足并网需要，传统的风力机在发电机和电网之间加装变频装置[1],或使用伺服电机来控制主轴转速[2]。这两种方式所使用设备均有成本高、体积大、质量大的特点，难以适应风力机大型化的趋势。新型前端调速式风力机组传动系统通过使用液力变矩器对风力机传动链主轴上的能量进行分流，用以调节主轴转速，因而风力机传动链变为复杂的刚-柔体系统[3-5]。控制液力变矩器导叶开度来调节液力变矩器工作油循环流量，调节涡轮输出转速，并通过液力机械传动装置作用在主轴上，可使发电机前的主轴输出转速稳定在恒定值。对该传动链系统的建模和仿真分析将对系统的匹配计算、结构优化设计以及整体控制起到非常重要的指导作用。

1　传动链结构分析

除风轮、齿轮箱、传动轴、发电机外，前端调速式风电机组传动链还增加了液力变矩器以及液力机械传动装置，其连接方案如图1所示。

图1　前端调速式风电机组传动链结构示意图

为适应不断变化的风轮转速，在发电机前的主轴处，将风轮从风中所吸收的功率分流出一部分，输送给导叶开度可调的液力变矩器。借助于液力变矩器变转矩变转速的调节作用，分流出的功率经过机械传动装置回流至主轴的输入端太阳轮，与来自齿轮箱的功率合并。来自齿轮箱和液力机械传动装置的两方面的输出转速综合作用于主轴，调节主轴转速，使之趋于稳定。该传动链的调速核心为液力机械调速装置,它可利用分流的小部分功率调节发电机的转速。

图1中,从风轮至发电机共有三级行星轮，第2级行星轮转速关系满足

ωt=(1+b)ωj-bωq

(1)

式中,b为第2级行星轮结构参数;ωt为太阳轮转速，rad/s;ωj为行星架转速,rad/s;ωq为外齿圈转速，rad/s。

第3级行星轮中行星架固定，转速为0,其转速关系满足

c=-ωT/ωq

(2)

式中,c为第3级行星轮结构参数;ωT为涡轮转速，rad/s。

2　风速模型的建立

随机性是自然风的主要特点。对自然风风速的模拟可采用恒速风、阵风、阶跃风、随机风相结合的方法[6],如图2所示。图2中,tG为阵风起始时间,t1G为阵风持续时间,vGmax为阵风风速峰值,t为时间,tR为阶跃风起始时间，t1R为阶跃风终止时间,vRmax为阶跃风风速峰值,vG为阵风风速,vR为阶跃风风速,vW为模拟自然风风速。本文取恒速风风速、阵风峰值风速、阶跃风峰值风速均为4m/s。

图2　风速模型

3　风轮空气动力学模型的建立

根据贝兹理论,风轮只能吸收自然风中有限的一部分能量。实际风轮转矩可按下式计算:

(3)

λ=RωR/v

式中,PR为风轮机械功率,W;ωR为风轮转速,rad/s;λ为叶尖速比;CP为功率系数;TR为风轮转矩,N·m；ρ为空气密度,kg/m3;R为风轮半径,m;v为风速,m/s;β为风轮桨距角,(°)。

CP可以按下式计算[7]：

(4)

根据式(3)、式(4)建立风轮气动模型，如图3所示。

图3　风轮空气动力学模型

4　传动链动力学模型的建立

采用刚性轴模型，建立齿轮箱输入端前的低速轴动力学方程:

(5)

式中，T1为低速轴输出转矩，N·m；JR为风轮和低速轴转动惯量,kg·m2；c1为低速轴阻尼系数。

在齿轮箱部分,忽略转动惯量,其转矩关系可按下式计算:

T1=aT2

(6)

式中,T2为齿轮箱输出转矩;a为齿轮箱增速比。

建立液力机械传动装置的动态平衡方程：

(7)

式中,Tt1为第1级行星轮太阳轮输入转矩,N·m;Tt2为第2级行星轮太阳轮输出转矩,N·m;TB为液力变矩器泵轮输入转矩,N·m;TT为液力变矩器涡轮输出转矩,N·m;To为同步发电机输入转矩,N·m;Jt1为发电机前主轴转动惯量,kg·m2;Jt2为液力变矩器输出轴转动惯量，kg·m2；ωo为主轴转速,rad/s;ωT为液力变矩器涡轮输出转速,rad/s。

忽略高速轴转动惯量,得到高速轴动力学方程:

(8)

式中,Te为同步发电机电磁转矩,N·m；Je为同步发电机转子转动惯量,kg·m2;ce为高速轴阻尼系数。

由文献[8-9]可知,根据转速及转矩关系式可以得到

(9)

式中,Tq为外齿圈传递转矩,N·m;Tj为行星架传递转矩,N·m。

在外齿圈位置,两层齿圈所传递的力矩相等，即Tq1=Tq2。同时,对式(9)中第一式求导，则可导出

(10)

式中,a为第1级行星轮的结构参数。

为使液力变矩器在高效区域内工作,应综合考虑结构参数的取值[5]。本文所取结构参数为:a=25,b=1.9,c=2.5。

根据以上关系式可以得出

(11)

其中,系数J1、J2、J3、J4、f1、f2满足下式：

(12)

根据式(5)～式(12)建立求解模型,如图4所示。

图4　传动链转速方程组求解模型

5　液力变矩器动态模型的建立

本文选用文献[10]的研究结果作为液力变矩器的建模依据。其泵轮力矩系数满足

0.15887iTB+0.6915+0.49x-0.49)×10-6

(13)

式中,x为液力变矩器导叶开度;iTB为液力变矩器转速比。

泵轮转矩可按下式计算：

(14)

式中,ρ1为工作油密度,取826 kg/m3;nB为泵轮转速;λB为泵轮力矩系数；D为循环圆直径,取700 mm,g为重力加速度,取9.8 m/s2;λB为泵轮力矩系数。

根据文献[10]的研究结果，涡轮转矩可按下式计算：

(15)

其中,a0、a1、a2为导叶开度系数，其表达式为

(16)

根据式(13)～式(16)可以建立图5所示的液力变矩器的仿真模型。

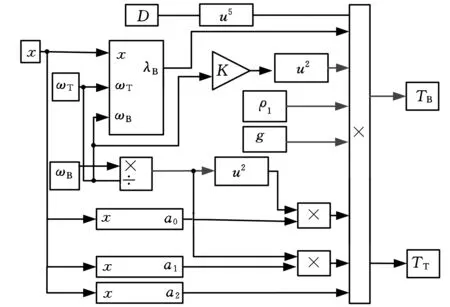
图5　液力变矩器仿真模型

6　主轴转速合成关系分析

由图1可以看出，发电机前的主轴转速主要受两方面的影响，一方面是来自风轮通过变速箱最终作用在主轴太阳轮上的转速，另一方面是来自液力变矩器通过液力机械部分的传动齿轮最终作用在主轴太阳轮上的转速。两者的转速在太阳轮上合成，共同决定主轴的转速。可根据转速关系式(9)建立主轴转速计算模型。

7　神经网络控制模型的建立

神经网络控制的目标是解决复杂的非线性和不确定的控制问题，具有很好的稳定性、鲁棒性。针对一定的系统设计生成神经网络并加以训练，可以达到很好的控制效果。在MATLAB/Simulink中可以很方便地进行神经网络控制模块的搭建和设置[11]。

8　传动链系统仿真与结果分析

利用Simulink软件,将第2章至第7章所述各子系统仿真模块进行封装,并给定空气密度、风轮半径、桨距角、风轮转动惯量、太阳轮转动惯量、发电机转子转动惯量、阻尼系数等参数。同时,为保证仿真结果的准确性，添加限幅模块，限定风轮的转速小于额定转速，并保证主轴的转速值为正值。建立前端调速式风力机传动链系统整体仿真模型,如图6所示。系统整体仿真模型内嵌了图2所示的风速模型，图3所示的风轮空气动力学模型，图4所示的传动链转速方程组求解模型，以及液力变矩器仿真模型。系统中各参数取值如表1所示。

表1　风力机传动链分析参数表

根据所建立的传动链整体模型在Simulink中进行模拟仿真,得到风轮气动功率系数CP,风轮转矩TR以及主轴转速ωo的计算结果,如图7～图9所示。其中图9即为XY-Graph的输出图形。

图6　风力机传动链整体系统仿真模型

由图7可以看出,风轮功率系数随风速的变化有波动变化。考虑到气动模型的经验性和不完善性,忽略个别波动较大的值,可以得出CP值总体保持在0.42附近,符合贝兹理论,且能够适应风速的变化,保证了风力机的最大风能捕获能力,符合设计初衷。

由图8可以看出,虽然实现了风能最大的捕获能力,但在风力机运行过程中，风轮的实际输出转矩却随风速的大小而有较大范围的波动变化，这将造成传动链输入转速的不确定性。

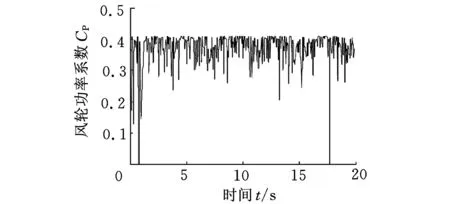
图7　风轮功率系数曲线图

图8　风轮转矩曲线图

图9　风力机传动链主轴转速曲线图

由图9的主轴转速仿真结果可以看出,随着风力机的启动,主轴转速逐渐增大，约5 s时达到峰值，之后逐渐回落并稳定在157 rad/s,即1500 r/min附近,达到了设计要求。主轴转速的动态响应时间为4s左右,最大偏差约为6%。主轴转速基本稳定后,受风速波动的影响,虽有小幅波动但是波动幅值约为2 rad/s,变化量约为1.27%。

由此可见,通过引入神经网络控制，调节液力变矩器的导叶开度可以改变液力变矩器的输出转矩，进而改变其输出转速，以适应输入转速的不确定性，可以最终保证主轴转速恒定。

综合上述分析可得:该仿真模型可较好地响应风速的变化;在机组稳定运行时可以最大限度地捕获风能，并使主轴转速稳定在设计值附近；传动链整体传动质量基本满足风力机设计需求；该建模方法可行。

9　结论

(1)基于Simulink软件建立了传动链各子系统及整体模型仿真模型,实现了前端调速式风力机组传动链的模拟仿真。通过引用神经网络控制，控制导叶开度来调节液力变矩器的工作油循环流量，从而改变液力变矩器的输出转矩和转速，以适应变化的风轮转速，使主轴转速稳定在设计值。

(2)模拟结果表明,风轮功率系数随风速变化，其值宏观上保持在0.42附近,保证了风力机的最大风能捕获量,符合设计初衷。

(3)满足最大风能捕获量时，风轮的输出转矩随风速变化波动，造成输出转速变化。通过在传动链中使用导叶开度可调型液力变矩器和神经网络控制,可以很好地跟踪风速的变化，使主轴转速保持恒定。

(4)传动链主轴转速在仿真时间5 s左右达到峰值，由峰值时间经过3 s后趋近于157 rad/s。主轴转速的动态响应时间为4 s左右,最大偏差约为6%。在主轴转速基本稳定后约有2 rad/s的误差,变化量约为1.27%。

本文得出的仿真结果达到了传动链的设计目的。如果进一步对液力变矩器进行合理匹配,并在随机风速下对传动结构进行优化,得到最优的结构参数，则可使输出转速进一步达到更加稳定的状态，起到调节转速，提高传动质量的目的，使风力机可以直接并网发电，省去变频器等设备。该传动系统模型的建立对前端调速式风力机组传动链的建模与仿真有一定的借鉴意义，为优化传动系统提供了参考。

[1]Li Shuhui,Haskew T A,Ling Xu,et al.Conventional and Novel Control Designs for Direct Driven PMSG Wind Turbines[J].Electric Power Systems Research,2010,80(3):328-338.

[2]Zhao Xueyong,Maiber P.A Novel Power Splitting Drive Train for Variable Speed Wind Power Generators[J].Renewable Energy,2003,28(13):2001-2011.

[3]Williams R,Smith P.Hydraulic Wind Turbines?[J].Machine Design,2010,82(7):40-42.[4]Thomsen K E,Dahlhaug O G,Niss M O K,et al.Technological Advances in Hydraulic Drive Trains for Wind Turbines[J].Energy Procedia,2012,24:76-82.

[5]闫国军,董泳．风力发电液力机械传动装置的特性及设计[J].太阳能学报,2012,33(4):571-576.

Yan Guojun,Dong Yong.Characteristics and Design of Hydro-mechanical Transmission Device[J].Acta Energiae Solaris Sinica,2012,33(4):571-576.

[6]陈虎,孟克其劳,马建光.基于MATLAB的风力发电机组建模和仿真研究[J].节能技术,2012,30(1):24-28.

Chen Hu,Meng Keqilao,Ma Jianguang.The Modeling and Simulation Study of Wind Turbine Based on MATLAB[J].Energy Conservation Technology,2012,30(1):24-28.

[7]张琦玮,蔡旭.最大风能捕获风力发电系统及其仿真[J].电机与控制应用,2007,34(5):42-46.

Zhang Qiwei,Cai Xu.Maximum Wind Energy Tracking Wind Turbine System and Simulation[J].Electric Machines & Control Application,2007,34(5):42-46.

[8]董泳,王洪杰,周绪强.风力发电系统液力变速与传动应用技术研究[J].热能动力工程,2008,23(6):670-675.

Dong Yong,Wang Hongjie,Zhou Xuqiang.A Study of the Applied Technology of Hydraulic Speed Variation and Transmission for Wind Power Generation Systems[J].Journal of Engineering for Thermal Energy and Power,2008,23(6):670-675.

[9]邵金华,何玉林,金鑫,等.新型变速风力发电传动系统的研究[J].现代制造工程,2007(6):112-115.

Shao Jinhua,He Yulin,Jin Xin,et al.Investigation of A New Transmission System of the Alter Velocity Wind Turbine[J].Modern Manufacturing Engineering,2007(6):112-115.

[10]杜魏魏.风力发电可变导叶液力机械调速装置研究[D].长春:吉林大学,2011.

[11]李国勇.神经模糊控制理论及应用[M].北京:电子工业出版社,2009.

(编辑苏卫国)

Modeling and Simulation of Front-end Speed Adjusting Wind Turbine Drive Train

Li Rennian1,2Liu Xin1,2Liu Shujun1,2

1.Lanzhou University of Technology,Lanzhou,730050 2.Wind Energy Technology Research Center of Gansu Province,Lanzhou,730050

Based on the new type of wind turbine drive train,analyses of the key parts were carried out,and the mathematical models were established.Simulation models of wind speed,wind turbine aerodynamics,hydraulic torque converter and spindle speed were established.Including the neural network control model,all models were integrated to establish the whole drive train simulation model.Then,the calculation and simulation were carried out.Based on the maximum wind energy capture,considered the structure parameters of the drive train,the guide vane opening of the hydraulic torque converter was controlled by the neural network to adjust the working oil circulation flow. Then, the torque and the speed of the converter were changed. Through planetary gears, the spindle before the generator was drived by the output of the converter and the output of the wind rotor together, to make the spindle speed stabilized at the design value.

wind turbine;drive train;hydraulic torque converter;modeling and simulation

2013-11-05

国家高技术研究发展计划(863计划)资助项目(2012AA052902)

TK83DOI：10.3969/j.issn.1004-132X.2015.04.010

李仁年,男，1963年生。兰州理工大学能源与动力工程学院教授、博士研究生导师。主要研究方向为流体机械及工程、多相流、风力机械。发表论文70余篇,出版专著2部。刘鑫,男,1982年生。兰州理工大学能源与动力工程学院硕士研究生。刘姝君，男，1987年生。兰州理工大学能源与动力工程学院硕士研究生。