敏捷卫星同轨多条带拼幅成像模式研究

余婧喜进军于龙江蒋方华

（1北京空间飞行器总体设计部，北京 100094）（2清华大学航天航空学院，北京 100084）

敏捷卫星同轨多条带拼幅成像模式研究

余婧1喜进军2于龙江1蒋方华2

（1北京空间飞行器总体设计部，北京 100094）（2清华大学航天航空学院，北京 100084）

针对长宽均明显大于相机幅宽的区域目标的成像观测，文章建立了敏捷卫星同轨多条带拼幅成像工作模式。对区域目标的划分，用相机视场角随卫星姿态机动扫描将区域分割成多个条带，使得划分的条带能够完全覆盖目标区域，并保证相邻条带之间足够的重叠宽度。对区域划分后得到的条带，分析了可行的观测序列，建立了成像起始时刻优化模型，采用序列二次规划方法对该模型进行求解。

敏捷卫星；同轨拼幅；区域划分；任务规划；序列二次规划

1 引言

敏捷卫星是指能够在短时间内实现大角度快速机动的卫星，利用其快速姿态机动能力，能够迅速改变星上相机对地指向，实现对地面目标的高效、灵活的观测，敏捷是其最形象的表述。鉴于成像的灵活性与高效性，敏捷卫星已成为当今遥感卫星的重要发展方向，世界不少国家已成功发射或正在研究敏捷卫星。比较典型的有美国的艾科诺斯（Ikonos）系列、世界观测卫星（Worldview）系列，法国的昴宿星（Pleiades）系列等，国内目前已开展相关研究工作。

敏捷卫星可沿三轴进行转动，具有快速调姿能力，基于其优异的姿态机动性能，敏捷卫星可以实现多种新型的成像工作模式，如同轨多点目标成像、同轨多条带拼幅成像、同轨多角度成像等。其中同轨多条带拼幅成像是指卫星通过快速姿态机动来调整相机指向，对区域目标连续进行多次扫描成像以实现对区域的完全覆盖。对于宽度与长度明显大于相机成像幅宽的区域目标，常规卫星星上相机一次扫描不能完成对区域目标的完全覆盖成像，因此需要将区域目标分解为多个可观测的条带，并利用敏捷卫星的强机动能力，实现对一较大区域的快速成像。

国内外均针对这种拼幅成像工作模式进行了大量的研究。对于区域目标的成像观测问题，一般将其分解为区域目标划分与同轨拼幅成像任务规划两个子问题。

针对区域目标的划分，Lemaitre［1］将不规则的多边形区域目标分割成了相互平行的矩形长条带，分解时需确定条带的方向与偏移量，对于不同的条带，其宽度是相等的，但长度是不固定的。

文献［2］对Lemaitre的区域分割方法进行了改进，考虑卫星可观测范围的限制，采用了一种有重叠的分割方法，缩短相邻条带之间的距离。国防科技大学相关学者［3］提出了区域目标动态分解方法，采用了卫星在不同侧摆角下对区域的覆盖范围作为分解的依据。杨剑［4］针对多星区域目标成像调度问题，提出了带时间标记的成像条带模型，设计了约束可满足的区域目标分解方法。向仍湘［5］考虑了敏捷卫星对地观测的特点，将杨剑提出的带时间标记的成像条带模型方法进行改进，使之适用于敏捷卫星成像情形下区域目标的分解。

关于敏捷卫星成像任务规划模型的建立与求解，文献［6-8］以Pleiades卫星为例，建立了轨道选择与成像任务优化模型，采用多种方法（贪婪算法、动态规划算法、约束规划算法、局部搜索算法［6-7］与禁忌搜索算法［8］）进行求解并比较了各种算法的优劣。此外，有文献采用排列搜索与约束传播结合算法［9］和遗传与模拟退火混合算法［10］对该问题进行了求解。

本文详细地探讨了敏捷卫星同轨多条带拼幅成像工作模式中的区域划分、观测序列确定以及成像起始时刻求解等问题。用相机视场角随卫星姿态机动扫描对区域目标进行了划分，使得划分的条带能够完全覆盖目标区域，且相邻条带之间具有足够的重叠宽度，然后建立优化模型分析多条带的观测序列，选择最优的观测序列。通过仿真算例表明，所设计的同轨多条带拼幅成像工作模式是有效的。

2 同轨多条带拼幅成像模式

同轨多条带拼幅成像工作模式是指卫星通过快速姿态机动来调整相机指向，对区域目标连续进行多次同向扫描成像以实现对区域的完全覆盖。这里的区域目标是宽度与长度均明显大于星下点摄影时幅宽的目标。其工作原理如图1所示，图中MS表示卫星开始本次成像任务时对应的星下点，ME表示卫星结束本次成像任务时对应的星下点，Bs_i表示第i个条带（i=1，2，…，n；区域目标用n个条带拼接完成，图1中n取4）相机开始成像时对应的星下点，Cs_i表示第i个条带相机结束成像时对应的星下点，Ai表示第i个条带成像准备时刻相机光轴指向的地面点，Bi表示第i个条带成像开始时刻相机光轴指向的地面点，Ci表示第i个条带成像结束时刻相机光轴指向的地面点。

图1 同轨多条带拼幅成像工作模式原理示意图Fig.1 Sketch of one-orbit multi-stripes splicing imaging picture

该模式旨在实现对一较大区域的快速成像，每次扫描时滚动角与俯仰角在扫描过程中不发生变化，偏航角需要进行修正，实现像移补偿，扫描方向为沿迹正向，要求卫星对一个条带扫描结束后，进行俯仰反向机动，并侧摆一定的角度，使卫星指向平移约一个幅宽的距离，同时需要保证相邻两个条带之间有一定的重叠宽度，以便于后期的图像处理。

同轨多条带拼幅成像工作模式的设计，需要解决区域目标如何划分成可观测的条带目标、条带观测序列的确定以及每个条带观测起始时刻的求解等问题。

3 区域条带划分算法

对于区域目标，其宽度与长度明显大于相机幅宽，卫星一次推扫不可能完成对区域目标的完全扫描成像，需要将其拆分成多个条带进行扫描。对于区域目标条带的划分，可以基于相机星下点摄影幅宽，也可以基于相机视场角，本文采用基于相机视场角的方法。

星下点轨迹与区域的位置关系，有两种可能情形（见图2）:①星下点轨迹与区域无交点或仅有一个交点，②星下点轨迹与区域有两个交点。对于后一种情形，星下点轨迹把区域分为左右两侧，对于每一侧的区域，其区域条带划分算法可以按照星下点轨迹与区域无交点或者仅有一个交点的情形处理。下文先介绍星下点轨迹不经过区域情形下的区域条带划分算法。

图2 星下点轨迹与区域的位置关系Fig.2 Position relationship between sub-track and area target

假设相机视场角为θFOV，相邻条带重叠区域宽度为doverlap，卫星对区域可见开始时刻为ts，可见结束时刻为te，持续可见时间Δt=te—ts，将Δt五等分，计算用到的3个时刻为和定义（λ，φ）为某点的经纬度坐标，其中λ表示经度，φ表示纬度。我们取与对应的星下点（λ1，φ1），（λ2，φ2）来确定星下点轨迹方程:

式中:（x，y）表示星下点轨迹的经度和纬度。通过星下点轨迹方程，可以判断星下点轨迹与区域是否相交，并采取相应的区域划分方法。

下面对所提到的一些概念进行定义和明确。

（1）视场角θFOV:遥感器的实际视场角，由遥感器高度、焦距和探测器尺寸决定。

（2）视场角θFOV_new:考虑相邻条带之间的重叠doverlap后的虚拟视场角，小于遥感器的实际视场角。

（3）条带边界、条带顶点、起始结束扫描点如图3（a）所示。条带边界，遥感器视场角θFOV对应的条带沿星下点轨迹方向的两条边界；条带顶点，过每个条带的最下与最上端点作两个边界的垂线，总共产生4个交点，这4个交点也即该条带的4个顶点，即图中的Vi_j（i表示第i个条带，i=1，2，…，n；j表示条带的第j个顶点，j=1，2，3，4；区域目标用n个条带拼接完成）。起始结束扫描点:条带的起始扫描点是最下两个顶点的中点（星下点轨迹由下往上），或最上两个顶点的中点（星下点轨迹由上往下）；相应的，另一侧条带两个顶点的中点即为相应的结束扫描点；在图3（a）中分别用Mi_up和Mi_down表示。

图3 条带和成像区域相关概念示意图Fig.3 Sketch of concepts about strip and area target

（4）区域顶点:如图3（b）所示，①②③④⑤⑥为区域顶点。区域顶点矩阵可表示为P=［（λ1，φ1）（λ2，φ2）……（λ6，φ6）］。

图4给出区域的多条带划分的示意图，图中的区域目标由5块条带拼接而成。条带之间的重叠宽度为:doverlap；A0，A1，A2，A3，A4分别为条带1，2，3，4，5的靠近星下点轨迹一侧的条带边界；A5为条带5的远离星下点轨迹一侧的条带边界。

图4 区域目标的多条带划分Fig.4 Multi-stripes partition of area target

3.1 计算划分视场角

考虑相邻条带重叠区域宽度为doverlap，不能用视场角θFOV直接进行划分，而需要用较小的视场角θFOV_new进行划分，来保证相邻条带之间的重叠。

式中:a为轨道半长轴，Re为地球平均赤道半径。考虑相邻条带拼接时，需要保留一定的重叠区域，设为doverlap，则θFOV对应的幅宽为

如图4和图5所示，对于划分得到的一个条带来说，条带之间需要重叠doverlap，θFOV_new为

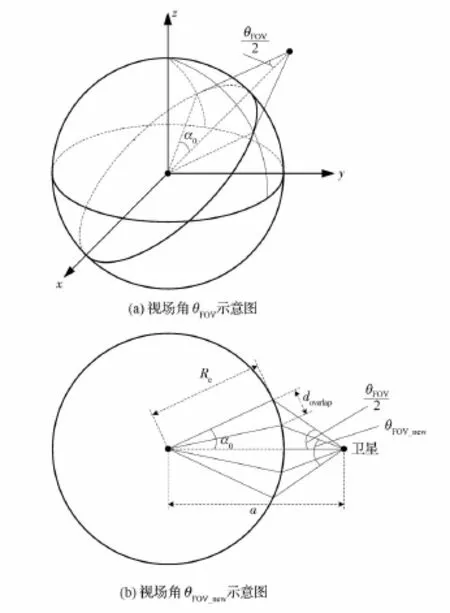
图5 地心角计算示意图Fig.5 Sketch of geocentric angle calculation

3.2 确定条带数量

根据可见的中间时刻tmid和滚动角计算方法，可得到此时刻卫星对区域所有顶点的滚动角，用滚动角最大值与最小值之差Δφ及视场角θFOV_new可确定条带数量n。

对n0向上取整，即可得到条带数量n。

以上的区域划分算法是基于星下点摄影时的幅宽进行划分的，在卫星机动成像时，幅宽较星下点成像会增加，造成相邻条带重叠宽度超过设定的宽度，但差异不会很大，且重叠区域较多更便于后期的图像拼接。

3.3 求解条带边界与区域边界的交点

设区域顶点矩阵为P，Pj1表示第j个顶点的经度，Pj2表示第j个顶点的纬度，调整区域顶点矩阵P中各点的顺序，使得P中的第一个点为离星下点最近的点。显然第一个条带靠近星下点轨迹一边的边界方程为y—P12=k（x—P11），该方程与区域的交点即（P11，P12）。而其他的条带边界方程需由该边界方程向左或向右平移得到，条带边界与区域边界的交点通过联立条带边界方程与区域边界方程求解得到。

对于第i个条带来说，靠近星下点轨迹的边界方程可以由第i—1个条带靠近星下点轨迹的边界来获得，下面给出第i个条带靠近星下点轨迹的边界方程的求解方法。

考虑区域位于星下点轨迹的一侧，其滚动角或全为正，或全为负。

对于全为正的情形，卫星对第i个条带靠近星下点轨迹的边界的滚动角为

式中:φmin为第一个条带（最靠近星下点轨迹的条带）靠近星下点轨迹边界，即图4中的A0对应的滚动角。

对于滚动角全为负的情形，φ为—|φ|，此时第一个条带（最靠近星下点轨迹的条带）靠近星下点轨迹边界对应的滚动角φ绝对值最小，但为负值，所以为φmax，此时卫星对第i个条带靠近星下点轨迹的边界的滚动角为

3.4 求解条带4个顶点与起始结束扫描点

比较各个条带边界与区域边界的交点、以及区域各顶点的位置关系，确定每个条带的最下与最上端。为求解条带的4个顶点，还需求解每个条带考虑了重叠宽度后的边界方程。

对于第i个条带，滚动角全为正的情形，卫星对其靠近星下点轨迹的边界的滚动角为

卫星对其远离星下点轨迹的边界的滚动角为

对于滚动角全为负的情形，卫星对其靠近星下点轨迹的边界的滚动角为

卫星对其远离星下点轨迹的边界的滚动角为

根据时刻t1及φnear_i可以计算得到卫星指向的地面点（λ1，φ1），根据时刻t2及φnear_i可以计算得到卫星指向的地面点（λ2，φ2），由（λ1，φ1）与（λ2，φ2）可确定第i个条带靠近星下点轨迹的边界方程fnear_i。根据时刻t1及φfar_i可以计算得到卫星指向的地面点（λ3，φ3），根据时刻t2及φfar_i可以计算得到卫星指向的地面点（λ4，φ4），由（λ3，φ3）与（λ4，φ4）可确定第i个条带远离星下点轨迹的边界方程ffar_i。由条带边界方程fnear_i与ffar_i，以及条带的最下与最上端即可确定四个顶点及起始结束扫描点。

3.5 区域与星下点轨迹有两个交点的情形

对于区域与星下点轨迹有两个交点的情形，区域被星下点轨迹分为左右两侧，对于每一侧分别按照按3.1～3.4节介绍的方法求解即可。

4 同轨拼幅任务规划模型

4.1 观测序列

对于区域划分得到的多个条带，卫星对其进行观测，需要确定条带的观测序列与每个条带的观测时间。对于处在星下点轨迹同一侧的条带，其观测顺序要么是从距离星下点轨迹开始由近及远观测，要么是从距离星下点轨迹由远及近观测。所以，对于星下点轨迹不过区域的情形，其可能的观测序列有2种，见图6；对于星下点轨迹穿过区域的情形，其可能的观测顺序有8种，见图7。

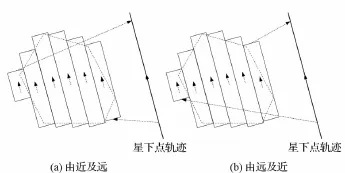
图6 同轨多条带拼幅成像可能的观测顺序（星下点轨迹不过区域情形）Fig.6 Possible observation sequences when the sub-track is not through area

对于每一种观测序列，需要建立优化模型来求解每个条带的观测起始时刻，使得卫星在整个成像过程中的侧摆角累计和最小。这里的侧摆角指的是卫星滚动、俯仰后相对星下点总的机动角度。再比较所有观测序列的优化指标函数值，从中选择较优的观测序列。

图7 同轨多条带拼幅成像可能的观测顺序（星下点轨迹穿过区域情形）Fig.7 Possible observation sequences when the sub-track is through area

4.2 起始成像时刻优化模型

显然，每个条带成像起始时刻的求解问题是一个典型的具有约束的非线性规划问题，即在满足一定约束的条件下，寻找最优的成像起始时刻，使得整个成像过程中卫星的侧摆角累计和最小。下式为非线性规划问题的通用数学表达式。

式中:f（χ）为以χ为自变量的指标函数，c（χ）为非线性不等式约束，ceq（χ）为非线性等式约束，A与b为线性不等式约束的左端矩阵和右端值；Aeq与beq为线性等式约束的左端矩阵和右端值，lb与ub为自变量χ取值允许的下界和上界。

4.2.1 优化指标

由于单条带成像过程中卫星的滚动角与俯仰角保持不变，可以所有条带成像的起始侧摆角的平方和最小为优化指标。

4.2.2 优化变量

选取每个条带的起始成像时刻作为被优化量，变量的维数与条带的数目一致。这里，记变量为χ。

4.2.3 变量约束

利用STK软件中的Access Tool工具，可以获得对各个条带目标的可见时间段，假设第i个条带的可见开始时刻为 （ts）i，可见结束时刻为（te）i。从而变量的下界为可见开始时刻，变量的上界为可见结束时刻。可见开始时刻的数学表达式为

式中:i为条带序号；n为条带数目。

4.2.4 线性约束

假设成像任务间机动时间的最小值为10 s，即上一次成像结束与相邻的下一次成像开始之间的时间间隔大于10 s。

4.2.5 非线性约束

这里的非线性约束主要有:①成像准备时刻—成像开始时刻≤0；②可见开始时刻—成像开始时刻≤0，这个约束其实与变量的下界约束是一致的；③成像结束时刻—可见结束时刻≤0。这里的成像准备时刻是指卫星上一次成像任务结束后，并机动到下一次成像起始姿态所对应的时刻。

4.2.6 初值选取

由于变量维数与条带数目一致，对于每个条带来说，可以选取可见开始时刻与可见结束时刻之间的中间时刻作为优化求解的初值。

4.2.7 优化指标函数求解

对于每一个条带来说，需要求解的成像数据有:成像准备时刻、成像开始时刻、起始经度、起始纬度、起始滚动角、起始俯仰角、起始偏航角、起始侧摆角；成像结束时刻、结束经度、结束纬度、结束滚动角、结束俯仰角、结束偏航角、结束侧摆角。在已知第i—1个条带的信息后，需要计算得到第i个条带的信息。

对于区域划分后的条带，已知第i个条带的起始点经纬度与条带长度，起始时刻为待优化量，其他信息与优化指标函数的求解流程如下:

（1）根据起始时刻、起始点经纬度及条带长度计算结束时刻、结束点经纬度；

（2）计算卫星对起始点的滚动角、俯仰角与偏航角，由滚动角与俯仰角计算起始侧摆角；

（3）计算卫星对结束点的滚动角、俯仰角与偏航角，由滚动角与俯仰角计算结束侧摆角；

（4）由第i—1条带结束点的姿态角与第i个条带起始点的姿态角计算条带之间的卫星机动角度。

定义卫星轨道坐标系So（o，x，y，z）:坐标原点o，卫星在轨时质心的位置；坐标z轴，从卫星质心指向地心；坐标x轴，在轨道平面内垂直于z轴指向前（与速度方向夹角小于90°）；坐标y轴，由右手螺旋定则确定。此坐标系随卫星运动而动，具有轨道角速度ωn。定义卫星姿态坐标系Sa（o，x1，y1，z1）:坐标原点o，卫星质心；坐标系三轴指向，三轴指向由卫星轨道坐标系分别绕x轴、y轴和z轴转动顺序（1-2-3 Euler角转序）形成，转动角度分别为卫星在三轴上的姿态偏差补偿。在此设定滚动角为φ，俯仰角为θ，偏航角为φ。

卫星对第i—1个条带成像时，由姿态系到轨道系的转换矩阵为

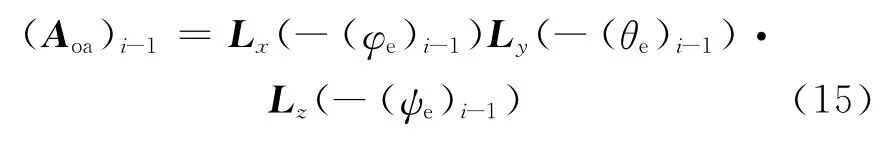
卫星对第i个条带成像时，由轨道系到姿态系的转换矩阵为

对于同一个条带，有（Aao）i（Aoa）i=E，E为单位矩阵。

计算卫星从第i—1次成像到第i次成像在姿态系下的转换矩阵为

计算卫星从第i—1次成像到第i次成像的机动角度为

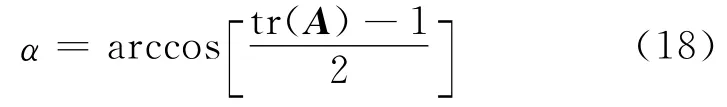
（1）根据成像条带之间的机动角度及卫星姿态机动速度能力计算机动时间；

（2）第i次成像的准备时刻=第i—1次成像的结束时刻+机动时间；

（3）优化指标函数为起始侧摆角平方和。

求解流程见图8所示。

图8 条带成像数据与指标函数求解流程Fig.8 Process for calculation of imaging data indicator function

4.2.8 模型求解方法

对于非线性规划问题，有多种求解方法且较为成熟，如遗传算法、粒子群算法、模拟退火算法等，这里，使用序列二次规划方法对该问题进行求解。

5 结论

针对区域目标的敏捷成像问题，本文设计了敏捷卫星同轨多条带拼幅成像工作模式。采用基于相机视场角的划分方法将区域目标划分成多个可观测条带，建立了同轨拼幅任务规划模型将条带观测问题分解为观测序列确定及成像起始时刻优化求解两个子问题。通过比较所有观测序列的成像期间侧摆角平方和，确定最优观测序列，对于每种观测序列下的成像起始时刻求解，建立了非线性规划模型，采用序列二次规划方法对每个条带的成像起始时刻进行求解。通过仿真算例表明，所设计的区域划分算法对同轨多条带拼幅成像工作模式是有效的。本文所设计的同轨多条带拼幅成像工作模式可为敏捷卫星成像模式设计和优化实际工程应用提供参考。

（

）

［1］Lemaitre M，Verfaillie G，Jouhaud F，et al.Selecting and scheduling observations of agile satellites［J］.Aerospace Science and Technology，2002，6（5）:367-381

［2］阮启明，谭跃进，李菊芳，等.对地观测卫星的区域目标分割与优选问题研究［J］.测绘科学，2006，31（1）: 98-100 Ruan Qiming，Tan Yuejin，Li Jufang，et al.Research on segmenting and selecting of area targets［J］.Science of Surveying and Mapping，2006，31（1）:98-100（in Chinese）

［3］白保存.考虑任务合成的成像卫星调度模型与优化算法研究［D］.长沙:国防科技大学，2008 Bai Baocun.Study of mathematic model for ISSP-TM and optimization algorithm［D］.Changsha:National University of Defense Technology，2008（in Chinese）

［4］杨剑.基于区域目标分解的对地观测卫星成像调度方法研究［D］.长沙:国防科学技术大学，2009 Yang jian.Study of satellite imaging scheduling methods based on region decomposing［D］.Changsha:National University of Defense Technology，2009（in Chinese）

［5］向仍湘.敏捷卫星任务调度技术研究［D］.长沙:国防科学技术大学，2010 Xiang Rengxiang.Study of scheduling of agile earth observing satellite［D］.Changsha:National University of Defense Technology，2010（in Chinese）

［6］Lemaitre M，Verfaillie G，Jouhaud F，et al.How to manage the new generation of agile earth observation satellites［C］//Proceedings of the International Symposium on Artificial Intelligence，Robotics and Automation in Space.Toulouse:CNES，2000:1-10

［7］Verfaillie G，Lemaître M.Selecting and scheduling observations for agile satellites:some lessons from the constraint reasoning community point of view［C］//Principles and Practice of Constraint Programming 2001.Cyprus:Springer Berlin Heidelberg，2001:670-684

［8］Habet D，Vasquez M.Saturated and consistent neighborhood for selecting and scheduling photographs of agile earth observing satellite［C］//The 5th Metaheuristics International Conference.Kyoto:CNRS，2003: 281-285

［9］Dilkina B，Havens B.Agile satellite scheduling via permutation search with constraint propagation［EB/OL］.（2005-05-31）.［2014-05-05］.http://www.cs.sfu.ca/CourseCentral/827/havens/papers/topic#12（Satellite-Scheduling）/SatelliteSched.pdf

［10］Li Y，Xu M，Wang R.Scheduling observations of agile satellites with combined genetic algorithm［C］//Proceedings the 3th International Conference on Natural Computation.New York:IEEE，2007（3）:29-33

（编辑：张小琳）

Study of One-orbit Multi-stripes Splicing Imaging for Agile Satellite

YU Jing1XI Jingjun2YU Longjiang1JIANG Fanghua2
（1 Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）
（2 School of Aerospace，Tsinghua University，Beijing 100084，China）

For imaging of area target whose length and width are both greater than the photography width，this paper proposes one-orbit multi-stripes splicing imaging for agile satellite.For the partition of area target，the partition algorithm based on camera field of view angle is designed to divide the area target into different strips，and a certain overlap width between adjacent stripes is ensured.Then the feasible observation sequences are analyzed and the start imaging time optimization model is built.For the solution of the optimization model，the sequential quadratic programming algorithm is used.

agile satellite；one-orbit multi-stripes splicing imaging；area partition；mission planning；sequential quadratic programming

TP79

A DOI：10.3969/j.issn.1673-8748.2015.02.005

2014-11-19；

2015-02-12

国家重大航天工程

余婧，女，工程师，从事航天器总体设计和载荷类研究工作。Email：yuj421@gmail.com。