非线性弹性转子-轴承系统稳定裕度数值分析

刘继华，陈立，罗载奇，李奕新，钱兴良

（中国燃气涡轮研究院，成都610500）

非线性弹性转子-轴承系统稳定裕度数值分析

刘继华，陈立，罗载奇，李奕新，钱兴良

（中国燃气涡轮研究院，成都610500）

基于互补群群际能量壁垒准则量化理论，提出了轨迹加速度-位移扩展相平面稳定裕度分析法，从理论分析、数值计算两方面验证了该方法的正确性。建立了采用Capone圆轴承非线性油膜力模型的弹性转子-轴承系统模型，并用数值积分和庞加莱映射方法，得到系统在某些参数域中的分岔图、轴心轨迹图、庞加莱映射图、时间历程图和频谱图，得出分岔失稳速度随质量偏心的变化规律：分岔速度随质量偏心的趋势是先减小后增大，拟合曲线符合三次高斯公式，拟合精度达0.998 2。数值分析结果为该类转子-轴承系统的设计和安全运行提供了理论参考。

旋转机械；转子-轴承系统；加速度-位移扩展相平面；非线性；稳定裕度；分岔失稳转速；质量偏心

1　引言

高转速轻结构是高速旋转机械的设计趋势，它提高了旋转机械的性能，但也引发出很多严重的问题［1］。比如原来能用线性理论得出的结果不仅误差大，而且无法解释实际中出现的自激振动、分岔、跳跃等现象［2］。动力机械工程中，具有强烈非线性的重要组成部分是油膜轴承转子系统［3-6］。

定性的稳定性分析只能确定某些特殊点系统是否稳定，而无法判断一个原来稳定的系统在参数小变化下是否还能保持稳定，也无法估计一个不稳定系统的参数如何变化、变化多少才能使其稳定。这时需采用稳定定量分析方法［7］。

薛禹胜院士在电力系统稳定性分析中提出的互补群群际能量壁垒准则量化理论，在国内外电力系统中得到成功应用［8］，后来又被引入到非线性转子系统中［9-10］。文献［11］采用动能差序列衰减指数法来衡量工频周期运动的稳定裕度。由于分析的是系统瞬态响应的数据，每次实验需用小重物敲击转子圆盘几次。这样不仅对转子系统有损坏，而且每次敲击的力度不同，所测的数据也会不同，从而造成一定的误差。

本文提出了基于轨迹的加速度-位移扩展相平面稳定裕度分析法，并从数学理论和数值计算两个方面求证其正确性。这种方法的好处是直接从稳态数据着手，避免敲击转子-轴承系统而产生的系统损坏。基于Capone圆轴承非线性油膜力模型，对弹性转子-轴承系统进行数值计算，得出系统随参数变化的稳定裕度变化。采用分岔图、轴心轨迹图、庞加莱映射图、时间历程图和频谱图分析转子盘中心振动响应，得出分岔速度随质量偏心的变化规律。

2　数学模型

分析对象为单盘对称转子，见图1，两端支撑为滑动短轴承。采用简单离散转子模型［12］，将图中的转子模型离散为三个质点，轴段处的质量分别离散到轴颈和轮盘处。单盘转子系统的离散模型如图2所示，两轴段等效为刚度k，轮盘处的阻尼为c1，非线性油膜力分别作用在两个轴颈处的质点上。

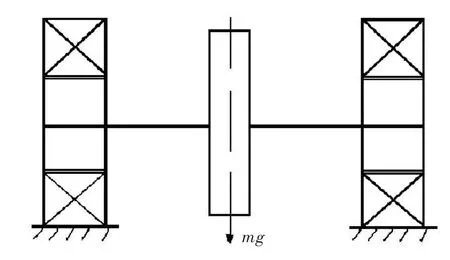
图1　单盘对称转子模型Fig.1 Mode of single-disk rotor

图2　单盘转子系统的离散模型Fig.2 Discrete mode of single-disk rotor bearing

参数采用无量纲处理，无量纲时间τ=wt；无量纲位移x=X/c，y=Y/c，c为轴承半径间隙（mm）。则无量纲速度，其中“⋅”表示d/dt，“′”表示d/dτ；无量纲偏心量ρ=e/c，e为偏心量（mm）；无量纲非线性油膜力分量［7］，；转子受到的无量纲重力；无量纲质量，其中δ为Sommerfeld修正数，反映润滑油粘度、轴承径向间隙及长径比等多因素的影响，，R为轴承半径（mm），L为轴承有效宽度（mm），η为润滑动力粘度（Pa·s）。可得出下列无量纲方程：

式中：fx、fy为无量纲非线性油膜力，其详细表达式参见文献［13］。

3　加速度-位移扩展相平面稳定裕度计算法

单自由度刚体系统在一个自由度上的运动方程为：

式（2）可变为：

将式（3）两边分别对δ积分，得到：

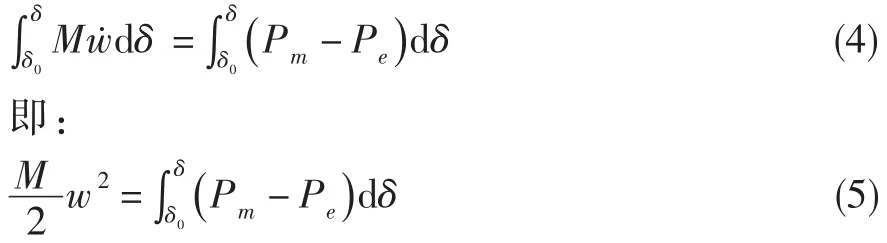
式中：M为广义惯量，Pm、Pe分别为广义驱动力和广义制动力，δ为刚体位移，w为刚体运动速度，为单刚体运动的等值加速度。式（5）的物理意义为：不平衡力对刚体所做的功转换为刚体的动能。刚体动能的变化可以用外力-位移扩展相平面（P-δ平面）上的面积来表达。

当M为常数时：

将式（6）代入式（5）可得出：

对于M为常数的系统，刚体动能变化也可用加速度-位移扩展相平面（γ-δ平面）上的面积来表达。，由于x存在二阶导数，一阶导数必连续，，所以。这就从理论分析上说明了。

图3为转速w=300 rad/s的周期解的加速度-位移扩展相平面，用MATLAB计算其闭合图形面积，得出S正=0.001 2，S负=0.001 2。这就从数值方面说明加速度-位移扩展相平面所围成的面积代数和为零。

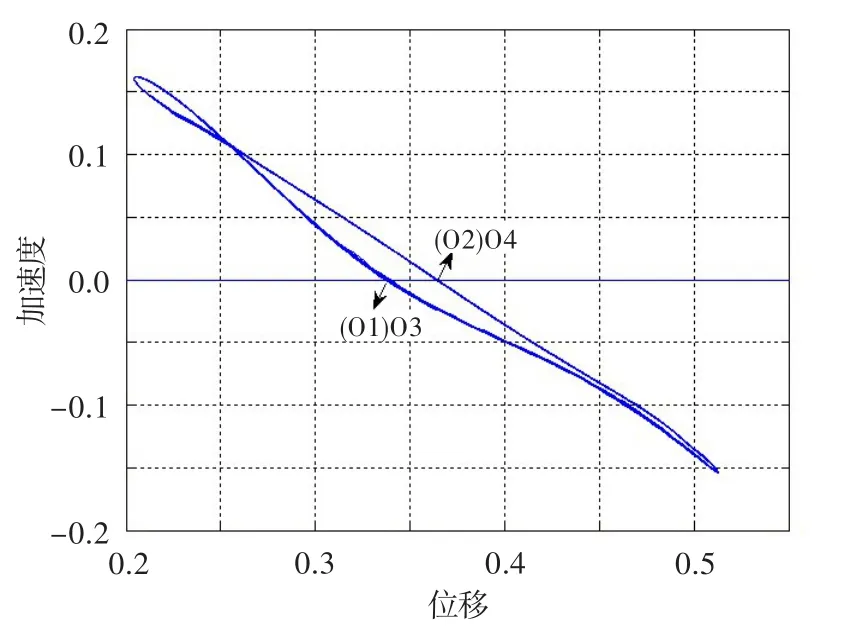
图3　转速300 rad/s时的加速度-位移扩展相平面Fig.3 Acceleration-displacement expansion phase plane dynamics（w=300 rad/s）

从数学理论和数值计算得出，对于M为常数的系统，对于稳态周期1解，系统每个周期T内，在γ-δ平面上所围成面积的代数和为零，即动能增加面积与动能减小面积相等。实际上，正面积的大小反应了系统贮存能量的多少，所以可用加速度-位移扩展相平面的正面积表示系统的稳定性。

4　数值计算分析

式（1）描述了一个非线性动力学系统的微分耦合方程，可以由数值计算得出近似解。本文使用MATLAB编程，由于油膜力和基座支撑力的强非线性作用，采用Rung-Kutta法求解。选用的时间步长为2π/100，误差小于10-6，计算1 500周期，取系统后500周期的响应，以消除其瞬态响应。系统稳定性分析时，选取如下转子模型参数［13］：m1=420 kg，m2= 50 kg，L=28.5 mm，c=0.2 mm，R=57 mm，η=0.018 Pa·s，k=2.105×108，c1=3×10 N·s/m。

4.1随转速增大的动态响应的分析

转轴和叶轮的加工及安装过程中，总会出现残余偏心量，使得转子系统在运转过程中产生振动。本节重点分析油膜支撑转子-轴承系统在偏心量-转速参数域内的稳定性及其分岔规律。ρ=0.1、w= 300 rad/s时系统的动态响应如图4所示。此时轴心轨迹为一个较规则的椭圆；Poincare图只出现一个离散的点；频谱图上只出现了一个工频；时间历程图为较规则的周期运动。由此可以判断，系统此时的运动表现为工频周期运动。

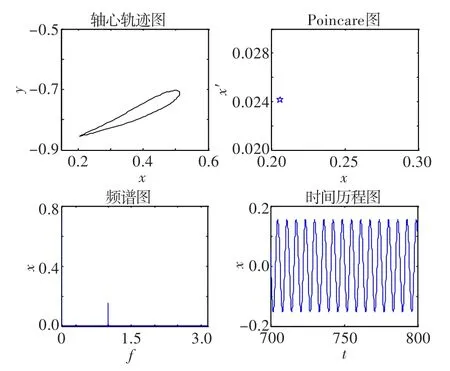
图4　无量纲偏心量为0.1转速为300 rad/s时的动态响应图Fig.4 Dynamic response diagram（ρ=0.1，w=300 rad/s）

进一步增大系统转速，系统同频运动周期发生分岔而失稳。ρ=0.1、w=500 rad/s时系统的动态响应如图5所示。轴心轨迹为不相交的内凹封闭曲线；Poincare图上表现为两个离散的点；频谱图上出现一个基频率和一个半频率，且半频率幅值比基频率幅值大；时间历程图为较规则的倍周期运动。由此可以得出，系统此时的运动表现为倍周期运动。

当转速升高到w=650 rad/s时，系统动态响应如图6所示。此时轴心轨迹为在一个圆环内相交的曲线；Poincare图为一些离散的点，但这些点形成一个封闭的形状；频谱图上出现了一些不可约分的频率。这些特点都说明，系统的运动表现为概周期运动。

4.2分岔图对比分析

进一步用数值计算方法得出系统在ρ=0.1时的全局分岔图，见图7。可见，w≤423 rad/s时都表现为周期运动，w＞423 rad/s时系统的同频周期运动发生分岔而失稳，424 rad/s＜w＜560 rad/s时为周期运动，570 rad/s＜w＜720 rad/s时系统由周期运动逐渐分岔为概周期运动。

图5　无量纲偏心量为0.1转速为500 rad/s时的动态响应图Fig.5 Dynamic response diagram（ρ=0.1，w=500 rad/s）

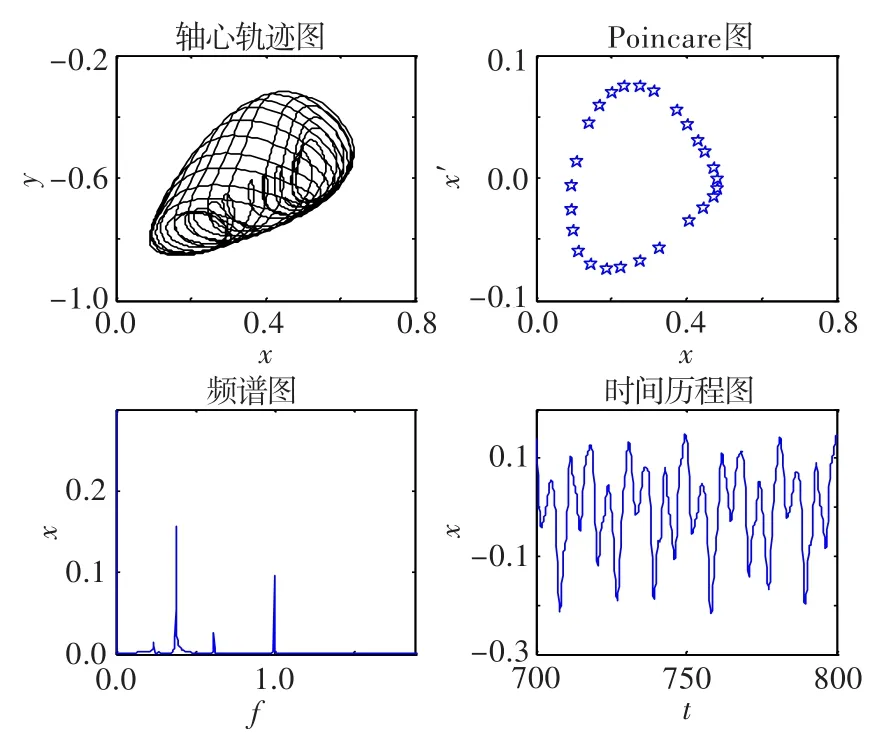
图6　无量纲偏心量为0.1转速为650 rad/s时的动态响应图Fig.6 Dynamic response diagram（ρ=0.1，w=650 rad/s）

图7　无量纲偏心量为0.1时的全局分岔图Fig.7 Global bifurcation diagram（ρ=0.1）

图8示出了ρ=0.4时的分岔细化图。可见，转速358 rad/s与360 rad/s之间只相差2 rad/s，但幅值却相差0.5个无量纲值，此时系统也没出现分岔现象。这种由外力强迫频率发生微小变化而振幅出现剧烈变化的现象，称为跳跃现象，为非线性所特有。

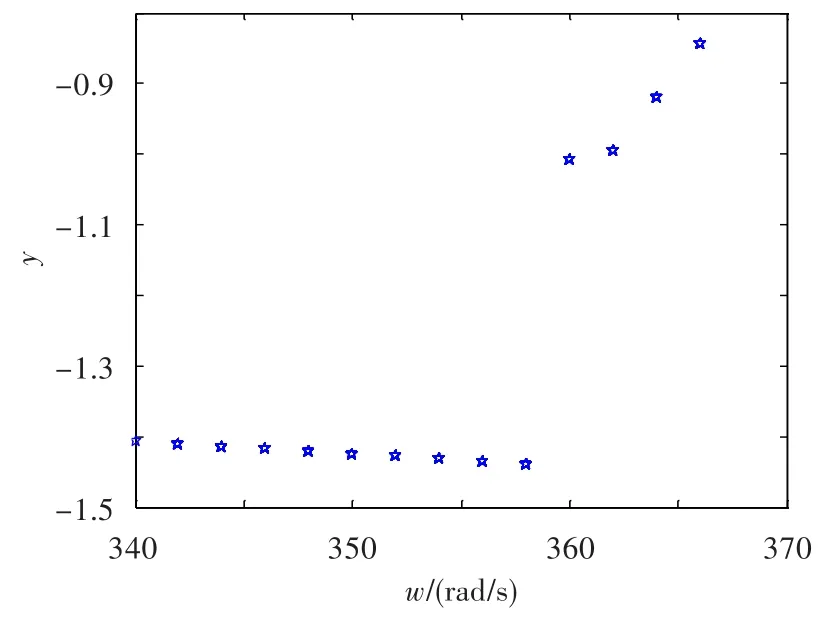
图8　无量纲偏心量为0.4时的分岔细化图Fig.8 Local bifurcation diagram（ρ=0.4）

由于不同的偏心量系统将出现不同的失稳特性，因此有必要研究偏心量变化对系统稳定的影响。从图9可知，随着偏心量的增大，开始时失稳转速不断降低；当无量纲偏心量增至0.25时，系统失稳转速又逐渐升高。较小和较大的不平衡量都会增大系统的稳定性，但较大的不平衡量会引起转子轴承受力增大，且有可能出现跳跃现象。因此，为确保系统安全运行，必须对转子进行较高精度的动平衡。

图9　转子轴承系统偏心量-转速参数域分岔集Fig.9 Bifurcation set of rotor bearing system with the parameter region of eccentricity and speed

对转子轴承系统偏心量-转速参数域分岔集进行拟合得出，三次高斯公式有很高的拟合精度，拟合度达0.998 2。失稳转速与偏心率、润滑粘度、轴承间隙、轴承宽径比等参数，形成一个三次高斯公式的表达式。

5　系统稳定性裕度的计算分析

5.1周期运动稳定裕度

周期运动的稳定裕度用加速度-位移扩展相平面上相比正面积准则，来衡量周期运动的稳定情况。首先画出某个周期运动的加速度-位移相平面图，计算出正面积；然后找出第一个周期分岔点，计算出临界正面积Acr；最后得出周期运动稳定裕度β。β值越小，系统的稳定性程度越差；临界状态时，β=0。

5.2倍周期运动稳定裕度

随着参数的变化，系统经倍周期分岔，其运动状态由周期运动变为倍周期运动。倍周期运动的明显特征是稳态时动能差序列为常数C1，该数值为一个周期内最大摆次中的最大动能与同向摆动的另一个摆次中最大动能的差值的绝对值，反映了倍周期运动中低频分量的大小及倍周期运动的剧烈程度。故把稳态时动能差序列之值加上负号，定义为倍周期运动的稳定裕度，即有：

C1越大，表示倍周期运动中的低频分量越大，倍周期运动越剧烈，系统的失稳程度越严重。临界状态时，β=0。

5.3概周期运动稳定裕度

鉴于概周期运动动能差序列的非周期特征，研究时必须选择合适的样本长度。取n个近似周期（本研究取10个近似周期），在动能差序列上依次截取形成一个样本序列。计算对应于每一个长度内动能差序列的数学期望（Ex），从而形成一个均值序列，该值反映了概周期运动动态中心点动能差的平均变化程度。因此，概周期运动的稳定裕度可以表示为：

β值越小，说明系统失稳程度越严重，概周期运动越剧烈。临界状态时，β=0。

5.4加速度-位移扩展相平面稳定裕度计算法求解

流程

通过上述分析，得出了不同运动的稳定裕度算法，按照以下流程，可以得出加速度-位移扩展相平面稳定裕度，从而确定系统的稳定裕度。

（1）做出系统的位移-加速扩展平面图，通过图上动态中心点的个数来判断系统所处运动状态。

（2）找出周期分岔点，求出其加速度-位移扩展正面积A+，并令其为临界面积。

（4）系统处于倍周期运动时，做出其速度序列图，求出速度峰值。

（5）系统处于概周期运动时，做出其速度序列图，取n个近似周期，求出速度峰值v1、v2…，动能差序列；然后求出Si的数学期望E（Si），β=-E（Si）。

5.5稳定裕度计算算例

采用加速度-位移扩展相平面稳定裕度计算法，求解式（1）中ρ=0.1时系统的稳定裕度变化规律。周期运动的稳定裕度变化规律如图10所示，可见系统周期运动时，随着转速的增大稳定裕度不断降低，具有很好的单调性，符合稳定性的概念。

图10　无量纲偏心量为0.1时周期运动的稳定裕度规律图Fig.10 Periodic motion stability margin（ρ=0.1）

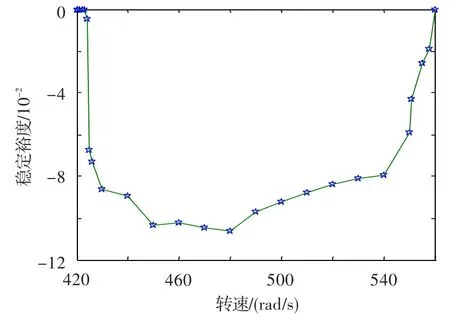
图11　无量纲偏心量为0.1时倍周期运动的稳定裕度规律图Fig.11 Double-periodic motion stability margin（ρ=0.1）

系统倍周期稳定裕度变化规律如图11所示。可见，转速为423 rad/s时，稳定裕度为-0.000 196 7，可近似为零。分岔图上的分岔失稳转速为423 rad/s，分岔点的稳定裕度为零。随着转速的增大，稳定裕度逐渐减小，当转速增大到480 rad/s时，稳定裕度的单调性开始出现转折；随着转速的继续增大，稳定裕度开始逐渐增大，当转速增大到560 rad/s时，稳定裕度逐渐趋于零。由前文分岔图可知，此时处在分岔点，重新回到工频周期运动。

系统概周期的稳定裕度变化规律如图12所示。可见，当转速低于580 rad/s时，系统的稳定裕度为零，结合分岔图可得出此时系统表现为工频周期运动。当转速超过580 rad/s时，系统开始逐渐变为概周期运动，稳定裕度逐渐下降。当转速增大到660 rad/s时，稳定裕度的单调性开始出现转折，随着转速的增大稳定裕度逐渐增大。

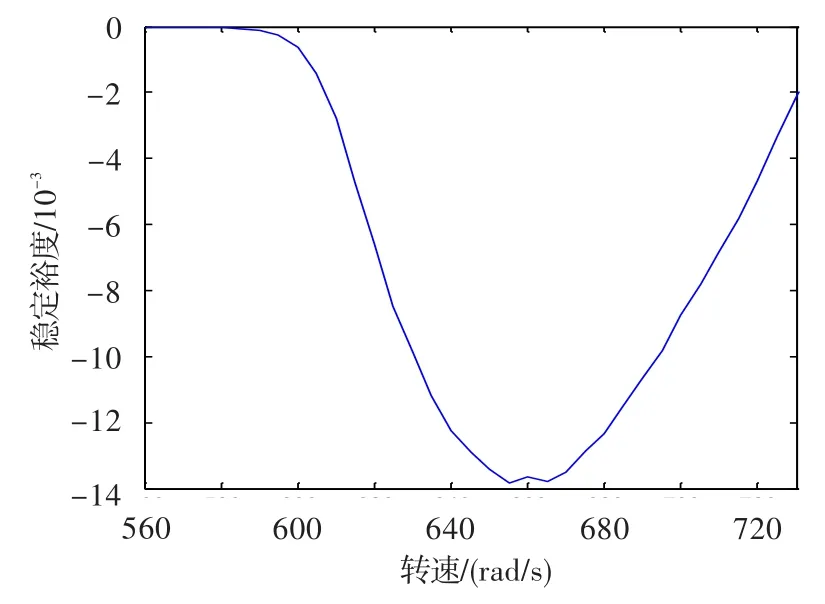
图12　无量纲偏心量为0.1时概周期运动的稳定裕度规律图Fig.12 Almost-periodic motion stability margin（ρ=0.1）

从以上分析可得出，基于轨迹的加速度-位移扩展相平面得出的稳定裕度为零的点，与通过Poincare映射法做出的分岔图上的分岔点，其对应转速基本相同，说明了这种方法的正确性。基于轨迹的加速度-位移扩展相平面方法不仅可以判断系统的分岔点，还具有其独特的优点。通过这种方法得出的稳定裕度可用来判断系统的稳定度和失稳度，适当改变系统的质量偏心、润滑油粘度、轴承间隙等参数可增加系统的稳定性；在保证系统稳定的条件下，增加系统的稳定裕度，使转子-轴承系统处于最佳的稳定性和安全性运行状态。

6　结论

（1）提出了轨迹加速度-位移扩展相平面稳定裕度分析法，从理论分析、数值计算两方面验证了该方法的正确性。

（2）偏心量较大的系统的失稳分岔速度较大，但偏心量较大其转子系统会存在跳跃现象的可能性，轴承受力增加；需对转子系统进行较高精度的动平衡，以保证系统的稳定性和安全性。

（3）对于稳态周期运动，系统每个周期内在加速度-位移扩展相平面上所围成面积的代数和为零。

（4）通过基于轨迹的加速度-位移扩展相平面得出的稳定裕度为零的点，与通过Poincare映射法做出的分岔图上的分岔点，其对应转速基本相同，说明了基于轨迹的加速度-位移扩展相平面方法的正确性。

（5）基于轨迹的加速度-位移扩展相平面方法，不仅可以判断系统的分岔点，还可以得出稳定裕度，从而判断系统的稳定程度。

［1］闻邦椿，顾佳柳，夏松波，等.高等转子动力学——理论、技术与应用［M］.北京：机械工业出版社，2000.

［2］刘延柱，陈立群.非线性振动［M］.北京：高等教育出版社，2001.

［3］Muszynska A.Partial lateral rotor to stator rubs［C］//.Proceedings of the 3rdInternational Conference on Vibration in Rotating Machinery.York UK：1984.

［4］Helio Fiori de C，Katia Lucchesi C，Rainer N.Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model［J］.Journal of Sound and Vibration，2008，371（1-2）：273—293.

［5］Yau H T，Chen C K，Chen C L.Chaos and bifurcation analysis of a flexible rotor supported by short journal bearings with non-linear suspension［J］.Journal of Mechanical Engineering Science，2000，214（7）：931—947.

［6］张新江，武新华.弹性转子-轴承-基础系统的非线性振动研究［J］.振动工程学报，2001，14（2）：228—232.

［7］黄文虎，夏松波.旋转机械非线性动力学设计基础理论与方法［M］.北京：科学出版社，2006.

［8］薛禹胜.运动稳定性量化理论［M］.南京：江苏科学技术出版社，1999.

［9］Xue Y S.The stability-preserving trajectory-reduction methodology for analyzing nonlinear dynamics［C］//.KeynoteinInternationalConferenceonInfo-tech&Info-net（IEEE Catalog Number 01EX479）.Beijing：2001.

［10］李银山，陈予恕，薛禹胜.非线性油膜力轴承上不平衡弹性转子的稳定裕度［J］.机械工程学报，2002，38（9）：27—32.

［11］陆永杰.滑动轴承转子系统稳定性量化分析方法的试验研究［D］.石家庄：河北科技大学，2009.

［12］闻邦椿，武新华.故障旋转机械非线性动力学的理论与实验［M］.北京：科学出版社，2004.

［13］Adiletta G，Guido A.Chaotic motions of a rigid rotor in short journal bearings［J］.Journal of Nonlinear Dynamics，1996，（10）：251—269.

Numerical analysis of stability margin for nonlinear vibration elastic rotor-bearing system

LIU Ji-hua，CHEN Li，LUO Zai-qi，LI Yi-xin，QIAN Xing-liang
（China Gas Turbine Establishment，Chengdu 610500，China）

A stability margin analysis method for the acceleration displacement of trajectory extension plane was proposed based on complementary-cluster energy-barrier criterion（CCEBC）of the stability of quantification theory.The correctness of this method is verified through theoretical analysis and numerical simulation.An elastic rotor bearing system was investigated based on the assumption of Capone bearing mode.The bifurcation diagrams，the shaft centerline orbit，Poincare maps，time histories and frequency spectrums of the system in some typical parameter regions were acquired by using the Poincare maps theory and numerical integration method.The results show that bifurcation speed varies as mass eccentricity changes.The speed decreased first and then increased，curve fitting with three times the Gauss formula and the fitting accuracy reached 0.998 2.The analysis results provide theoretical reference for designing and safely operating of this kind of systems.

rotating machine；rotor-bearing system；acceleration-displacement expansion phase plane；nonlinear；stability margin；bifurcation speed；mass eccentricity

O322；V231.96

A

1672-2620（2015）06-0039-06

2015-03-25；

2015-09-12

刘继华（1988-），男，贵州榕江县人，硕士，主要从事转子动力学、航空发动机起动研究。