应用土壤修正模型的返回器着陆冲击响应预示

王晓姝 赵会光

（北京空间飞行器总体设计部，北京 100094）

应用土壤修正模型的返回器着陆冲击响应预示

王晓姝 赵会光

（北京空间飞行器总体设计部，北京 100094）

在返回器着陆冲击响应预示研究中，土壤模型的准确建立是着陆冲击仿真的关键影响因素，由于土壤特性复杂，目前尚无完善描述冲击下的土壤本构关系模型。为此，文章根据已有的土壤模型，提出结合返回器刚体模拟器着陆冲击试验数据，利用多参数递进方法修正土壤模型中的体积模量、剪切模量和屈服参数，获得土壤修正模型。利用上述土壤修正模型，对刚体模拟器3种试验工况进行仿真，仿真结果与试验结果的误差在±10%以内，证明了修正模型的准确性。利用土壤修正模型对返回器柔性体模拟器建模，得到的柔性体模型着陆冲击仿真结果与试验结果有较高的吻合度。因此，土壤修正模型能准确预示着陆冲击，可为返回器优化设计提供参考。

返回器；着陆冲击；土壤模型；参数修正

1 引言

返回器在着陆时与地面发生接触，垂向速度在短时间内降为零，会产生比较大的冲击载荷。在冲击载荷作用下，返回器主/次结构、平台设备将产生一定的冲击应力、变形和加速度响应，因此，准确预示冲击环境及其影响是结构系统优化设计、确保任务成功的关键。返回器结构材料主要为金属，有关金属结构对返回器着陆冲击影响的研究已经较为成熟，因此要重点研究土壤模型参数对返回器着陆冲击的影响。

土壤在微观结构上具有晶粒结构、孔隙和微裂纹等特征，并且在孔隙或微裂纹中还含有液体或气体，因此土壤具有复杂的力学特性，并且在动力环境下的复杂性更为明显。相关参数的试验测量方法很多，但结果往往相差较大，如动态剪切强度，使用现场波速试验法与室内的动三轴、共振柱、动单剪和动扭剪等方法测得的数值往往相差若干倍［1］。因此，目前尚无完善的高能量冲击下的土壤本构关系模型。国外对着陆冲击的研究主要集中在试验和有限元仿真上，研究了不同类型的土壤（湿度、密度、成分）对返回器着陆冲击响应的影响［2-8］。国内的相关研究较少，只是提出返回器着陆冲击仿真要进行土壤参数调整［9］，或者研究了土壤参数对返回器着陆冲击响应的影响［10］。总之，对着陆冲击土壤模型的研究，很少关注如何调整土壤参数，也很少研究土壤参数变化对着陆冲击响应的影响趋势。为此，本文结合返回器刚体模拟器的着陆冲击试验数据，利用Patran&Dytran软件对刚体模拟器进行建模、仿真，针对国内返回器特定着陆区的土壤进行研究，并对该区的土壤模型进行多参数递进修正，通过对返回器柔性体模拟器的建模和着陆冲击仿真预示，证明了土壤模型参数修正方法的有效性和准确性，可为后续相关研究提供一定的参考。

2 多参数递进修正土壤模型

2.1 着陆场地面土壤模型

根据土力学有关理论，并考虑Patran&Dytran软件中提供的模型，本文使用可压垮泡沫材料模型。该模型用剪切模量、体积模量、屈服函数和拉伸破坏截止压力来描述［11］。模拟返回器着陆冲击，要考虑土壤的弹性性能、体积压缩性能以及其特殊的屈服特性［12-13］。

1）弹性性能

根据土力学的有关理论，土壤在冲击载荷下的变形模量与承受静态载荷时的静态变形模量，并没有很大的区别。比较波速试验和静力试验测得的泊松比发现，两者基本相同。通常，由波速试验测得小变形的土介质动变形模量，根据强夯时土壤的剪切模量约为小变形模量的1/10，得到冲击下的剪切模量，体积模量则是根据泊松比求得。

2）体积压缩性能

通过三轴等压试验，可以确定土壤的体积压缩性能。

3）土壤的屈服特性

对于土壤类的材料，载荷直接影响着其破坏性能。随着静水压力的增大，屈服应力也变大。土壤的屈服满足式（1）。

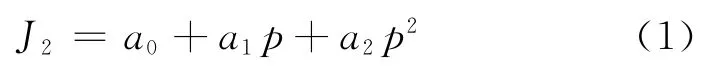
式中：J2为应力偏量的第二不变量；3个屈服参数a0，a1，a2体现了静水压力p对屈服的影响。

屈服参数a0，a1，a2通常利用土壤的三轴等压试验和无侧限的单轴压缩试验的试验曲线拟合获得，但是在建模过程中发现，这种方法应用起来非常困难，不但离散性大，而且有时会出现错误，而运用Ducker-Prager模型可以很好地解决这一问题。

Ducker-Prager模型表达式为

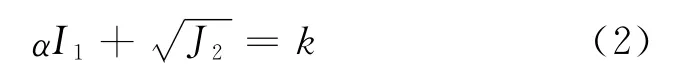
式中：I1为应力张量的第一不变量；分别为土壤的内摩擦角和粘聚力。

用Drucker-Prager模型作简单估计，进行一定的推导，可得

对比式（1）和式（3）可得

一般情况下，通过试验获得土壤内摩擦角φ和粘聚力c，可得到Ducker-Prager模型中的α和k，进而求得a0，a1，a2。

因此，可利用多参数递进方法修正的土壤模型参数有剪切模量、体积模量和3个屈服参数a0，a1，a2。

2.2 多参数递进修正方法

对土壤进行测量，得到表征土壤性能的参数，依据上述初始测量得到的参数进行土壤模型参数修正，修正过程如下。

（1）固定土壤体积模量和屈服参数（利用初始测量值），在一定范围内改变剪切模量的大小，进行仿真计算，与返回器刚体模拟器试验结果比对，得到与试验结果较为接近的剪切模量值。

（2）使用上述（1）中得到的剪切模量值和初始的屈服参数，在一定范围内改变体积模量，进行仿真计算，与该工况试验结果比对，得到与试验结果更为接近的体积模量值。

（3）根据式（4）可知，屈服参数a0和a1相关，a1和a2相关，改变a0或者a2，a1也随之改变，因此，只要对a0和a2加以调节即可。使用上述（1）、（2）中得到的剪切模量值和体积模量值，进行仿真计算，得到与试验结果较一致的屈服参数。

（4）利用其他工况的试验结果验证修正后的土壤参数。如果结果不在合理范围内，重新调整土壤参数。如果结果合理，修正结束，得到合理可用的土壤参数。

3 仿真分析

3.1 返回器建模

按照返回器的真实尺寸进行几何建模，包括刚体模拟器和柔性体模拟器建模，以获得刚体模型和柔性体模型。鉴于返回器实体模型的复杂性，为了有效地进行有限元建模，先要对返回器结构进行简化，保留主要承力结构。在简化过程中，尽量保证整体刚度、质量不变，关键部位形状一致，以保证关键部位仿真结果的可靠性。

（1）对刚体模拟器建模，简化为壳单元并划分网格。由于刚体模拟器在试验时不会发生较大变形甚至破坏，因此赋予材料属性为刚体，得到刚体模型。

（2）对柔性体模拟器建模要精细、复杂得多。根据实际情况，将不同部位简化为壳单元、梁单元和实体单元等。受应力较大、可能产生较大变形的区域，设置为弹塑性材料，其他区域采用线弹性材料，得到柔性体模型。

3.2 土壤模型参数修正

根据工程实际，为较全面地反映着陆工况，设定以下3种刚体模拟器试验工况。工况1：垂直速度13 m/s，水平速度0 m/s；工况2：垂直速度13 m/s，水平速度5 m/s；工况3：垂直速度13 m/s，水平速度10 m/s，以一定倾角着陆。着陆冲击仿真与试验工况一致。

用于着陆冲击试验的刚体模拟器由钢板和钢架组成，试验中返回器的结构变形很小，因此主要根据典型测点的加速度响应进行模型修正。根据试验结果，得到3种工况下测点的加速度峰值，再用加速度峰值进行参数修正。

土壤模型参数的初始测量值，如表1所示。

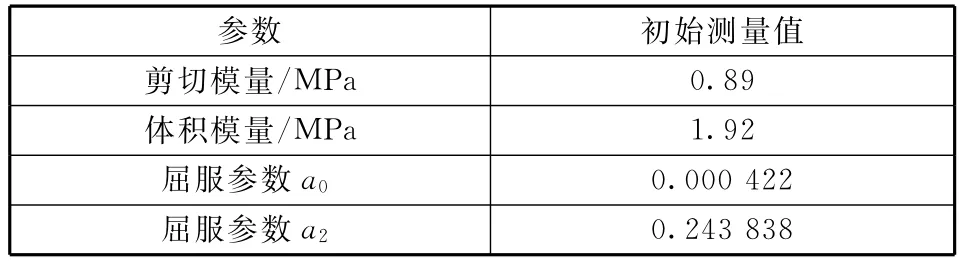
表1 土壤模型参数的初始测量值Table 1 Originally measured values of soil model parameters

（1）使用工况1试验结果进行参数修正。固定体积模量和屈服参数（利用初始测量值），在一定范围内改变剪切模量，进行仿真计算，获得的测点加速度峰值结果如图1所示。可以看出，随着剪切模量的增加，测点加速度峰值单调增加。当剪切模量小于0.10 MPa时，测点加速度峰值变化不明显；当剪切模量大于0.10 MPa且小于1 000.00 MPa时，测点加速度峰值逐渐增加；当剪切模量大于1 000.00 MPa时，测点加速度峰值大幅度提高。根据上述仿真结果规律，对比试验结果，得到合理的剪切模量值为8.85 MPa。

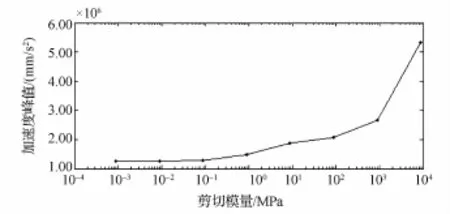
图1 不同剪切模量时的测点加速度峰值Eig.1 Peak acceleration of measured point for different shear modulus

（2）使用上述（1）中得到的剪切模量值和初始屈服参数，在一定范围内改变体积模量，进行仿真计算，获得的测点加速度峰值结果如图2所示。当体积模量较小时，随着体积模量的增加，加速度峰值略有提升；当体积模量继续增加，加速度峰值反而下降，体积模量在100.00～1 000.00 MPa时出现最小值；随着体积模量的继续增加，加速度峰值显著提高。根据上述仿真结果规律，对比试验结果，得到合理的体积模量值为19.20 MPa。

图2 不同体积模量时的测点加速度峰值Eig.2 Peak acceleration of measured point for different bulk modulus

（3）使用上述（1）、（2）中得到的剪切模量值和体积模量值，在一定范围内改变屈服参数a0，进行仿真计算，获得的测点加速度峰值结果如图3所示。可以看出：当a0小于0.000 010时，加速度峰值变化不明显；随着a0继续增加，加速度峰值迅速增加；当a0增加到一定程度后，加速度峰值不再改变。根据上述仿真结果规律，对比试验结果，得到合理的a0值为0.000 422。

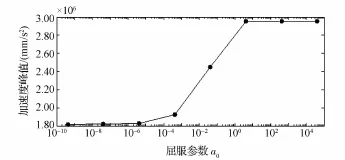
图3 不同屈服参数a0时的测点加速度峰值Eig.3 Peak acceleration of measured point for different yield parameter a0

（4）使用上述（1）、（2）、（3）中得到的剪切模量值、体积模量值和屈服参数a0，在一定范围内改变屈服参数a2，进行仿真计算，获得测点加速度峰值结果如图4所示。可以看出：当a2小于10.000 000时，随着a2的增加，加速度峰值增加显著；当a2大于10.000 000时，随着a2继续增加，加速度峰值增加趋于缓慢。根据上述仿真结果规律，对比试验结果，得到合理的a2值为0.343 838。

利用剪切模量值8.85 MPa，体积模量值19.20 MPa，a0值0.000 422，a2值0.343 838，获得工况1、工况2和工况3的测点加速度响应曲线，如图5所示。其中：工况1的测点加速度响应曲线峰值为2.07×106mm/s2，与试验结果2.04× 106mm/s2比对，误差为1.47%，满足要求。工况2的测点加速度响应曲线峰值为1.99×106mm/s2，与试验结果1.90×106mm/s2比对，误差为4.73%，满足要求。工况3的测点加速度响应曲线峰值为3.01×106mm/s2，与试验结果3.05× 106mm/s2比对，误差为1.31%，满足要求。

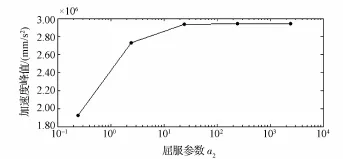
图4 不同屈服参数a2时的测点加速度峰值Eig.4 Peak acceleration of measured point for different yield parameter a2

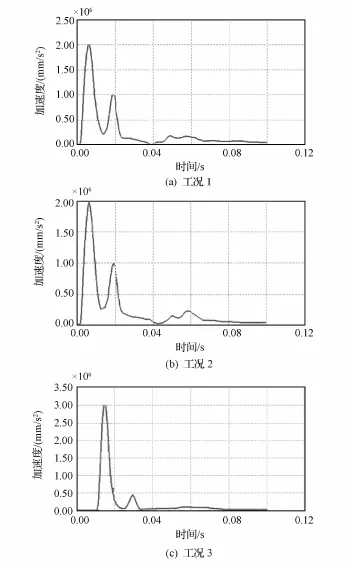
图5 3种工况的测点加速度响应Eig.5 Acceleration responses of measured point for three conditions

以上结果表明，通过多参数递进修正方法调整土壤模型参数，可使仿真结果与试验结果吻合较好，各工况下误差均在±10%以内，满足要求，可以利用此土壤模型作进一步分析研究。

3.3 柔性体模型仿真

为了验证上述修正后的土壤模型可以准确预示着陆冲击，以下对柔性体模拟器进行仿真。

1）后端框

如图6所示，后端框上靠近着陆处的应力明显较大，应力峰值为155 MPa，达到材料屈服强度。此外，后端框上与大梁连接处的附近区域，应力值也较大。

图7为后端框的塑性应变云图，可以看出，位于着陆点处附近的局部位置发生了塑性应变，最大塑性应变值为0.040 4，但未达到材料的断裂应变，没有出现断裂破坏情况。

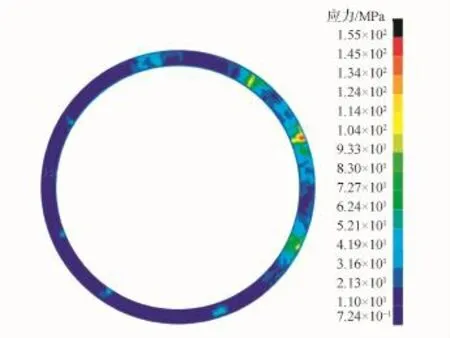
图6 后端框应力云图Eig.6 Bottom frame stress cloud

2）大梁

如图8所示，大梁上应力峰值最大为119 MPa，未达到材料的屈服强度。大梁上应力值较大位置主要位于大梁端头处及横纵梁中间位置附近区域。

图9为大梁的塑性应变云图，可以看出，大梁没有产生塑性应变。

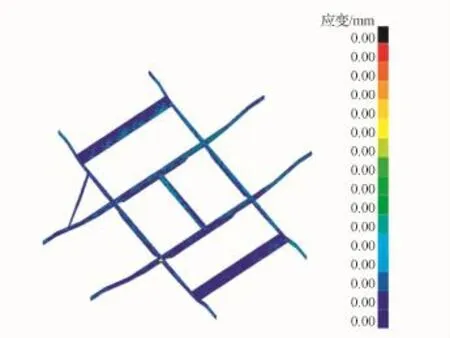
图9 大梁应变云图Eig.9 Girder strain cloud

在返回器柔性体模拟器着陆冲击试验中，大梁及后端框都没有发生破坏，后端框靠近着陆点附近产生了塑性变形，与仿真结果基本一致，证明修正后的土壤模型可以准确预示着陆冲击。

4 结束语

在返回器着陆冲击响应预示研究中，利用初始测量值获得的土壤模型的仿真结果与试验结果还有一定的差别。为了得到更合理的土壤模型参数，本文利用多参数递进方法对土壤模型参数进行修正，并最终得到了能够更准确模拟试验场土壤的模型，同时归纳了土壤参数对着陆冲击结果的影响规律，解决了返回器着陆冲击分析中土壤的准确建模问题。使用土壤修正模型对典型工况下柔性体模型的着陆冲击情况进行仿真，得到了柔性体模型主要结构的应力、应变结果，与试验结果有较好的吻合度，证明土壤修正模型的有效性，可准确预示返回器着陆冲击响应。

（

）

［1］陆培毅.土力学［M］.北京：中国建材工业出版社，2000 Lu Peiyi.Soil mechanics［M］.Beijing：China Building Materials Press，2000（in Chinese）

［2］Joseph V Welch.CEV airbag landing system modeling，AIAA 2007-2533［R］.Washington D.C.：AIAA，2007

［3］Timothy R Smith，Charles R Sandy，Joanne S Ware，et al.Orion CEV earth landing impact attenuating airbags-design challenges and application［C］//Proceedings of the 28th IEEE Aerospace Conference.New York：IEEE，2007：1-12

［4］Danny A Barrows，Alpheus W Burner，Eelecia C Berry，et al.Photogrammetric measurements of CEV airbag landing attenuation systems，NASA 20080008867［R］.Washington D.C.：NASA，2008

［5］Sydney Do，Olivier de Weck，Ricardo Robles Jr.An airbag-based crew impact attenuation system concept for the Orion CEV-first generation system development［C］//Proceedings of the Space 2009 Conference&Exposition.Washington D.C.：AIAA，2009：1-18

［6］Richard DeLoach.Design of Orion soil impact study using the modern design of experiments，NASA 20100003410［R］.Washington D.C.：NASA，2010

［7］Sydney Do，Olivier de Weck.Eeasibility study of an airbag-based crew impact attenuation system for the Orion MPCV，NASA 20110015920［R］.Washington D.C.：NASA，2011

［8］Mark Stephen D.Orion landing simulation eight soil model comparison，NASA 20090026521［R］.Washington D.C.：NASA，2009

［9］白远利，黄世霖，张金换.土壤在冲击过程中的建模研究［C］//第七届汽车安全技术会议论文集.大连：中国汽车工程学会，2002：77-83 Bai Yuanli，Huang Shilin，Zhang Jinhuan.Soil in the process of impact modeling research［C］//Proceedings of the 7th Automotive Safety Conference.Dalian：Society of Automotive Engineers of China，2002：77-83（in Chinese）

［10］贾世锦.返回舱结构缓冲仿真分析［C］//飞行器总体专业委员会2004年学术研讨会论文集.北京：中国宇航学会，2005：589-595 Jia Shijin.Structure of reentry capsule buffer simulation analysis［C］//Proceedings of the 2004 Aircraft Overall Professional Committee Conference.Beijing：Chinese Society of Astronautics，2005：589-595（in Chinese）

［11］卞文杰，万力，吴莘馨.MSC.Dytran基础教程［M］.北京：北京大学出版社，2004 Bian Wenjie，Wan Li，Wu Zixin.MSC.Dytran basic tutorial［M］.Beijing：Peking University Press，2004（in Chinese）

［12］王仁，黄文彬.塑性力学引论［M］.北京：北京大学出版社，1981 Wang Ren，Huang Wenbin.Introduction to plastic mechanics［M］.Beijing：Peking University Press，1981（in Chinese）

［13］龚晓南.土塑性力学［M］.杭州：浙江大学出版社，1999 Gong Xiaonan.Soil plastic mechanics［M］.Hangzhou：Zhejiang University Press，1999（in Chinese）

（编辑：夏光）

Returnable Capsule Landing Impact Response Based on Modified Soil Model

WANG Xiaoshu ZHAO Huiguang
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Establishing soil model accurately is a key factor affecting the landing impact simulation for the research on landing impact response of a returnable capsule.Due to the complexity of soil properties，there is no perfect description for soil constitutive relation under impact load.Therefore，in order to obtain suitable soil model，this paper combines original soil model with the rigid simulator landing impact test data to modify soil model parameters，including shear modulus，bulk modulus and yield parameters，by using the method of multi-parameter progressive modification.Three test conditions of rigid simulator by using modified soil model are simulated，and the simulation result error of each rigid model condition is less than±10%compared with the test result，so the soil model is usable.The simulation result of flexible model coincides with the test result by using modified soil model.The research shows that modified soil model can accurately predict landing impact，as well as provide a reference for subsequent optimization design of returnable capsule.

returnable capsule；landing impact；soil model；parameter modification

V415.4

A DOI：10.3969/j.issn.1673-8748.2015.03.008

2014-04-28；

2014-08-14

国家重大科技专项工程

王晓姝，女，硕士，助理工程师，从事航天器机械总体设计工作。Email：wxs926@126.com。