近地卫星地球反照系数的一种估计方法

李强 孙先伟 林乐天 高超 王巧 胡兴

（西安卫星测控中心，西安 710043）

近地卫星地球反照系数的一种估计方法

李强 孙先伟 林乐天 高超 王巧 胡兴

（西安卫星测控中心，西安 710043）

针对地球反照对近地卫星太阳电池阵的影响，分析卫星轨道与星下点的受照射情况，进而建立太阳电池阵输出电流模型，利用太阳电池阵电流的遥测数据，根据最小二乘法给出地球反照下的输出电流模型参数，然后利用延时遥测数据与拟合数据计算地球反照系数，同时分析地球反照对于太阳电池阵输出电流的影响，最后结合某低轨卫星的实际在轨测控数据进行验证。结果表明，对于630 km高度的近地卫星，地球反照系数在5%～8%之间；且随季节变化明显，从春至秋逐渐减小，从秋至春又逐渐增大；可为测控中的遥测诊断提供参考。

卫星；地球反照系数；太阳电池阵；电流；遥测

1 引言

近地卫星在太空中运行时需要太阳光提供能源［1］，利用太阳电池阵可以实现光能到电能的转换，太阳电池阵输出功率是卫星能源预算与平衡的重要依据［2］。太阳电池阵输出电流主要受到光照角度、太阳阵光电转换效率、入射点光照强度等因素影响，另外还受到地球反照（亦称地球反射）、卫星物理结构和几何造型、工作环境温度等因素影响。

地球反照主要有大气反照与地表反照两类，其中地表反照主要由地物镜面反射、漫反射形成。在传统研究中，一般较多地关注地球反照对卫星姿态控制系统的影响，例如对星敏感器［3］、太阳探头［4］等器件的干扰，对于能源方面的影响的研究相对较少［5］。国内对于地球反照的研究多集中于地球反照机理、建模方面，具体研究地球反照对于低轨卫星太阳电池阵输出电流影响的不多。在卫星测控与管理中，需要对遥测参数进行正确高效地诊断。

本文以某低轨卫星数据为例，对地球反照下的太阳电池阵输出电流进行量化估计，主要考虑季节因素变化，分析地球反照对于太阳电池阵输出电流的影响。首先根据日、地空间几何分析卫星轨道的光照、半影与本影，同时分析卫星星下点的光照、半影与本影，建立地球反照模型；然后分析太阳电池阵在空间中输出电流的变化模型，通过遥测数据拟合出轨道光照、地球反照同时存在时的太阳电池阵输出电流模型的参数以及电流曲线；最后结合实际在轨测控数据估计地球反照下的太阳电池阵输出电流变化系数。

2 地球反照与太阳电池阵输出电流

图1是轨道光照、半影与本影的形成示意图［6］。太阳与地球之间的两条内切线相交于Q点，其中一条与地球相切于A点；两条外切线相交于P点，其中一条与地球相切于B点；卫星在S点。显然，P点即为所谓的本影锥顶点，利用日地距离、日半径、地球半径等常数可以简单计算出本影锥高度约为1380 000 km，一般卫星远达不到这个高度。因此，绝大多数近地卫星在轨道上运行时都需要考虑光照、半影、本影的影响。

利用太阳星历以及卫星星历，可以计算出图1中的∠QEA与∠QEB、以及∠EQA与∠EPB。令地星矢量为dES，地日矢量为dEQ，计算dES与dEQ的夹角γ，同时还可以计算出矢量dSQ以及∠SQE、地影矢量dEP以及∠EPB和∠EPS，进一步可以判断卫星轨道的光照情况，下面给出简单算法。

（1）如果γ≤∠QEA，卫星轨道处于光照区域；

（2）如果∠QEA＜γ≤∠QEB：当∠SQE＞∠EQA时，卫星轨道处于光照；否则处于半影区域；

（3）如果γ＞∠QEB：当∠SQE＞∠EQA时，卫星轨道处于光照；当∠EPS＜∠EPB时，卫星轨道处于本影区域；否则处于半影区域。

以上对卫星轨道的光照与否进行建模分析，但对于地球反照还需要分析星下点的光照情况。

首先确定太阳的星下点与卫星的星下点，然后计算两个星下点的地心角α，利用地心角α和前面的计算结果，进一步判断卫星星下点的光照情况，其算法为：

（1）如果α≤∠QEA，卫星星下点处于光照区域；

（2）如果∠QEA＜α＜∠QEB，卫星星下点处于半影区域；

（3）如果α≥∠QEB：卫星星下点处于本影区域。

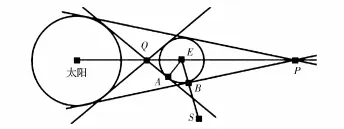
图1 光照、本影与半影Eig.1 Illumination，umbra and penumbra

图2为某晨昏轨道卫星某天的星下点与轨道光照情况示意图。这里用数值1表示光照，0.5表示半影，0表示本影，横轴为积秒值（单位为10 000s）。对于晨昏轨道，一年中大部分时间里，在一个轨道周期内，轨道是处于全日照状态。一年中小部分时间里，在一个轨道周期内，轨道呈现短时间段阴影。对于星下点而言，本影时长与光照时长几乎是相同的，半影时长可以忽略不计。对于本文为例的卫星，其降交点地方时［7］（Local Time of Descending Node，LTDN）为10：30AM，不属于晨昏轨道，其轨道、星下点的光照情况与图2中的星下点光照曲线（实线）相似。

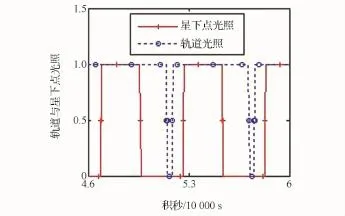
图2 星下点与轨道的光照情况Eig.2 Illumination of nadir and orbit

显然，研究地球反照对太阳电池阵的影响，需要考虑轨道与星下点的光照情况。在这里，选择轨道与星下点均在光照情况下的太阳电池阵输出电流数据进行地球反照系数估计。

仅考虑太阳入射角的影响，太阳阵电池的输出电流i可以用下式来表示。

式中：I0为太阳光直射时的太阳电池阵输出电流，其大小与太阳光照射的功率密度有关，在单位日地距离［8］下，太阳入射的功率密度为1535 W/m2。显然，距离越近，则功率密度越大，I0也越大；反之则越小。式（1）中β为太阳入射角［9］，定义为地日矢量与电池阵法向之间的夹角。显然，β越大，则输出电流越小。

在轨道上，卫星上的一些组件有可能遮挡阳光，造成太阳电池阵输出电流变化；另外，环境温度的变化也会影响输出电流的变化。在这里，只考虑日地距离、入射角、地球反照对输出电流的影响，假定其它因素对电流没有影响。

假定日地距离为r，卫星轨道半长轴为a。对于实际近地卫星轨道，一般可考虑偏心率为0，轨道高度在2000 km以下，则卫星至太阳的距离变化率δ定义为

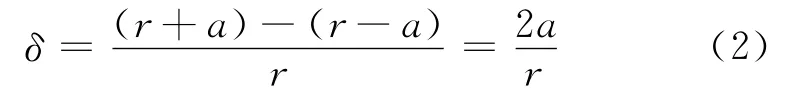
取轨道高度上限2000 km，将日地距离常数、地球半径带入式（2），可以得到δ为0.000 112，数值非常小。因此，卫星在一圈的运行之中，可以不用考虑卫星至太阳的距离变化对太阳电池阵输出电流的影响。

入射角对于太阳电池阵输出电流的影响最大，不同季节下的入射角各不相同。为减小入射角对于地球反照系数估计的影响，这里采用一年中春分、夏至、秋分、冬至附近的数据进行分析。

3 地球反照系数估计

图3为卫星太阳电池阵输出电流在一年时间中的变化情况，横轴为积秒，单位为10 000 s；纵轴为电流，单位为A；选取的时间为2014年3月21日、2014年6月21日、2014年9月21日和2013年12月21日，图中相应用实线、虚线、点划线、双划线表示。从图3中可见，每一圈中卫星必然经历光照与阴影变化，在光照区电流大于9 A，在阴影区电流接近于0。为讨论方便起见，以下将电流接近于0的区段称为零段，将电流大于9 A的区段称为非零段，且认为零段与非零段之间为阶跃跳变（这里暂不考虑半影的影响）。

可以看出，非零段的电流具有明显的双峰值特征，其原因解释如下：卫星刚从北极附近的阴影区进入光照区时，电流阶跃上升到某一数值；卫星继续前行，星下点纬度继续变大，由于太阳直射、大气折射、地表折射的关系，电流继续增加直至最大值；随后卫星向赤道方向继续运行，太阳电池阵在驱动机构作用下越来越背向地表，地球反照作用越来越小，在赤道附近位置，地球反照作用最弱，电流减小至最小值（非零段）；随后卫星继续向南极方向运行，电流呈现上述的反过程变化。因此，非零段电流具有双峰值特征。

对于前文所述非零段的双峰值之间的电流数据，可表示为

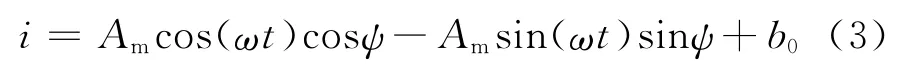
式中：Am为电流振幅，ω为轨道角速度，t为时间变量，ψ为初相，b0为均值（直流）。利用最小二乘法可以进一步求解具体参数：

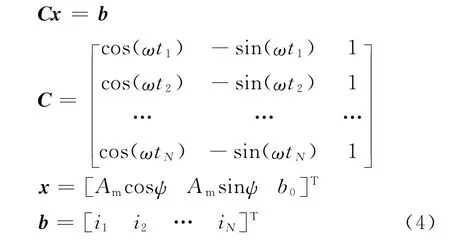
式中：N为采样数据的总点数。当N＞3时，式（4）为超定方程。将轨道角速度ω、时间变量t、电流数据i代入到式（4），即可求解得到电流振幅Am、初相ψ与均值b0。将求解得到的参数再代入到式（3），可以得到对应的拟合曲线。

图3 太阳电池阵输出电流遥测Eig.3 Solar array output current

图4即为卫星太阳电池阵输出电流的拟合曲线，图例同图3。可以看出，拟合曲线为正弦曲线，极值点不再与两极对应，而是与赤道对应。具体来说，在每一圈中，当卫星的星下点在向阳一侧的赤道附近时，电流最小；星下点在背阳一侧的赤道附近时，电流最大。如果将地球看成一个不挡光（全透光）球体，且反照特性不变，则在向阳侧太阳翼几乎完全挡光，地球反照对太阳电池阵的作用最弱；而在另一侧时，反照作用最强。正因为地球遮挡阳光形成阴影，导致电流在两极区域附近呈现阶跃变化，呈现双峰值特征。

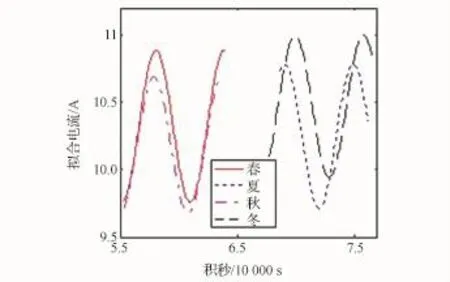
图4 太阳电池阵输出电流拟合Eig.4 Eitting solar array output current

这里给出两种不同数据源的地球反照系数估计方法。

第一种方法是利用图3中的遥测数据进行估计。先截取任一圈次遥测数据处于双峰值之间的非零段，假定双峰值点分别为（t1，i1）与（t2，i2）；再求解这段数据中的电流最大值与最小值，假定为imax与imin，定义地球反照系数γTM为

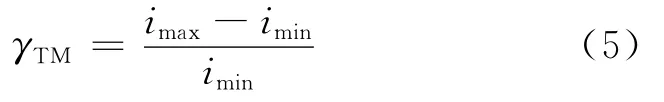
第二种方法是利用拟合数据进行估计。先利用第一种方法中的峰值点（t1，i1）与（t2，i2）确定时间段［t1，t2］，根据该时间段截取拟合数据；再从拟合数据中求解出电流最大值与最小值，假定为ifmax与ifmin，同样定义地球反照系数γf为

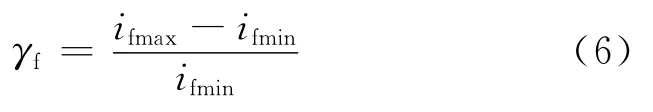
需要说明的是，无论式（5）与式（6），定义的反照系数都是以非零段电流中的最小值作为参考，而从以上分析可以知道，非零段电流实际上是一直有地球反照作用的，因此得到的反照系数只是一个相对值（相对系数）。更进一步，假定电流中的非反照部分为I（太阳照射产生的电流），地球反照最强与最弱时对应的反照电流对应为iS与iN，则反照系数γ可以重新定义为

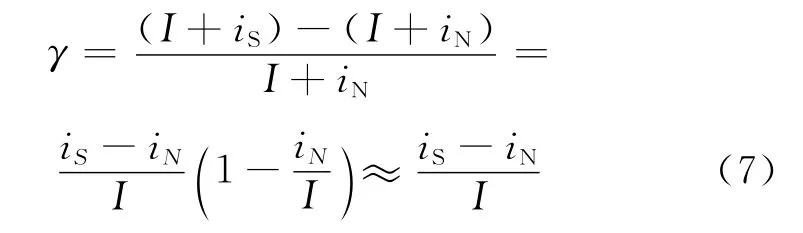
式（7）成立的条件是iN≪I，这个条件也基本符合前面的分析结果。从式（7）可以知道，式（5）与式（6）中定义的反照系数与太阳照射电流、地球反照电流都有关系。而照射电流在一年四季中是变化的，冬季最大，夏季最小，春、秋季居中。

4 验证

某卫星轨道高度约为630 km，近圆轨道（这里按照圆轨道考虑，偏心率e取为0），倾角为97.9°，降交点地方时为10：30AM。太阳电池为三结砷化镓太阳电池，太阳电池阵安装在卫星本体的±Y两翼上，以轨道角速度旋转。

利用式（5）与式（6），代入前面图3与图4中的数据，得到的地球反照系数估计结果如图5所示，横轴为春、夏、秋、冬4个特征时间点，纵轴为地球反照系数估计值（无量纲）。在图5中，由遥测数据直接得到的估计值结果按照春、夏、秋、冬的顺序为0.072 5、0.062 1、0.054 4、0.066 7；由拟合数据得到的结果对应为0.063 2、0.059 8、0.051 1、0.062 6。无论直接结果还是拟合结果，都是春季的估计值最大（最大值小于0.075），秋季的估计值最小（最小值大于0.05）；两种结果的曲线变化趋势也是基本一致的。虽然系数估计值在数值上有大小区别，但却难以区分地球反照的季节性强弱，原因在于太阳照射电流的季节变化。如果能够对太阳照射电流进行归一化处理，则可以分析地球反照的季节性强弱。此外，考虑到非零段的最小电流中已含有地球反照电流，真实的地球反照系数应该比图5中的估计值还要大一些。

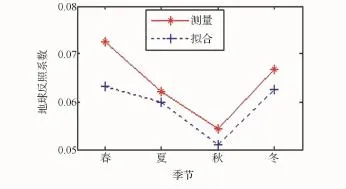
图5 地球反照系数估计Eig.5 Earth albedo coefficient estimation

根据以上结果，将卫星的地球反照系数保守取为0.05。

地球反照对于近地卫星的太阳电池阵输出电流有比较明显的影响，输出功率的变化对于在轨卫星管理与测控中的遥测参数诊断、电源分系统状态评估乃至卫星寿命估计都有重要参考价值。

5 结束语

地球反照对太阳电池阵输出电流的影响，利用遥测数据进行仿真，得到太阳电池阵输出电流模型参数和地球反照系数。估计结果表明，地球反照系数在5%左右。因此，近地卫星进入轨道后，经常会出现某些电源参数值稍高于地面设计值的情形，这里的估计结果可以为这种情形下的遥测诊断提供参考。同时还可以为卫星太阳电池阵输出功率估计提供参考。后续工作需要针对太阳照射电流进行归一化处理，以期得到更真实的地球反照系数结果。

（

）

［1］徐伟，鄢婉娟，刘元默.环境减灾-1A、1B卫星模块化电源分系统［J］.航天器工程，2009，18（6）：81-87 Xu Wei，Yan Wanjuan，Liu Yuanmo.HJ-1A，1B modularized power system［J］.Spacecraft Engineering，2009，18（6）：81-87（in Chinese）

［2］李小飞，乔明，陈琦.倾斜轨道卫星能量平衡优化分析方法［J］.航天器工程，2014，23（4）：52-56 Li Xiaofei，Qiao Ming，Chen Qi.Optimum analysis method of power balance for inclined-orbit satellite［J］.Spacecraft Engineering，2014，23（4）：52-56（in Chinese）

［3］张春明，解永春，王立，等.地球反照对星敏感器的影响分析［J］.激光与红外，2012，42（9）：1011-1015 Zhang Chunming，Xie Yongchun，Wang Li，et al.A-nalysis of influence of earth albedo on star tracker［J］.Laser&Infrared，2012，42（9）：1011-1015（in Chinese）

［4］夏项团，朱进兴，刘学明，等.地球反照辐射对太阳探头影响的研究［J］.红外与毫米波学报，2008，27（1）：27-30 Xia Xiangtuan，Zhu Jinxing，Liu Xueming，et al.Influence of earth radiation on sun sensor［J］.J.Infrared Millim.Waves，2008，27（1）：27-30（in Chinese）

［5］井元良，孙海涛，雷英俊.太阳同步轨道卫星太阳电池阵在轨特性分析［J］.航天器工程，2013，22（5）：61-66 Jing Yuanliang，Sun Haitao，Lei Yingjun.Analysis of performance of solar array for satellite in sun synchronous orbit［J］.Spacecraft Engineering，2013，22（5）：61-66（in Chinese）

［6］张世杰，曹喜滨.卫星进/出地影位置和时间的计算算法［J］.上海航天，2001，18（6）：19-22 Zhang Shijie，Cao Xibin.Calculating method of satellite entry and exit positions and times through umbra/penumbra［J］.Aerospace Shanghai，2001，18（6）：19-22（in Chinese）

［7］徐向华，程雪涛，梁新刚.圆形太阳同步轨道卫星的空间热环境分析［J］.宇航学报，2012，33（3）：399-404 Xu Xianghua，Cheng Xuetao，Liang Xingang.Analysis on space thermal environment for circular sun synchronous orbit［J］.Journal of Astronautics，2012，33（3）：399-404（in Chinese）

［8］彭梅，王巍巍，吴静，等.太阳同步轨道卫星太阳电池阵衰减因子研究［J］.航天器工程，2011，20（5）：61-67 Peng Mei，Wang Weiwei，Wu Jing，et al.Study on attenuation factor of si solar array for satellite in sun synchronous orbit［J］.Spacecraft Engineering，2011，20（5）：61-67（in Chinese）

［9］陈忠贵，张志，廖瑛.航天器太阳翼在轨光照角度建模与仿真分析［J］.航天器工程，2012，21（1）：37-42 Chen Zhonggui，Zhang Zhi，Liao Ying.Modeling and simulation analysis of solar illumination angle on spaceccraft solar wing in-orbit［J］.Spacecraft Engineering，2012，21（1）：37-42（in Chinese）

（编辑：李多）

Earth Albedo Coefficient Estimation to LEO Satellite

LI Qiang SUN Xianwei LIN Letian GAO Chao WANG Qiao HU Xing
（Xi'an Satellite Control Center，Xi'an 710043，China）

With respect to the earth albedo effect to LEO satellite solar array output current，and by considering the solar angle different from that in solar array driving mode，an output current model of solar array has presented to estimate amplitude，phase and direct current with least mean square that is used in the measured data processing.The earth albedo coefficient has been calculated in two different ways，one with original data of delayed telemetry and the other with fitting data of current estimation.Validated by LEO satellite engineering management in TTC，the final result has shown that the earth albedo coefficient is between 5%and 8%，descending from spring to fall and ascending from fall to spring and is a numerical reference to telemetry diagnose in TT&C.

satellite；earth albedo coefficient；solar array；current；telemetry

V556

A DOI：10.3969/j.issn.1673-8748.2015.03.003

2014-12-24；

2015-01-06

李强，男，工程师，从事在轨卫星测控与管理。Email：52215235@qq.com。