跨越直观 深入本质

周莹

“平行四边形面积”是小学传统的几何内容，10年间我先后三次执教该节公开课。随着教学经验的丰富与教学理念的不断更新，课堂教学从开始的“一味强调等积转化”到“用面积单位度量和等积转化平行展示”，最后“顺应学生思维实现两种方式的沟通”，真正帮助学生理解面积计算公式。这一变化让学生学习空间不断加大，教师也由讲授者慢慢向组织者与引导者转变。很好地达成了“引导学生在直观理解基础上，跨越直观达到本质理解”的课堂教学效果。

一、引入

1.知识回顾。（课件出示一个平行四边形）这是什么图形？四年级的时候我们认识了平行四边形，它有什么特点？

设计意图：一种图形的面积计算公式，从本质上说，是由它的形体特征所决定的。平行四边形之所以可以通过“剪、拼”的方式，转化为与它等底等高的长方形，利用长方形的面积计算公式求得面积，就是由它对边平行且相等的形体特征所决定的。正是这一特征，使得通过剪、拼的方法得到长方形的长和宽正好对应着原来平行四边形的底和高。本环节唤醒学生对平行四边形形体特征的认识，为后面自主研究平行四边形面积奠定基础。

2.引入新课。

师：今天我们来研究平行四边形的面积，要想知道这个平行四边形的面积是多少，你需要知道些什么？

生1：我想知道长和宽。

师：你上来指一下，你需要哪些数据？

（学生指了相邻的两条边，课后调查，很多学生把平行四边形的两条相邻的边自主迁移为平行四边形的长和宽。）

师：你是打算研究一下这两条边和面积之间的关系。

生2：我想知道高。

师：刚才这两位同学都是想要平行四边形边和高的数据，不用数据可以吗？

生3：用数格子的方法也可以的。

师：你想用面积单位来测量一下……

设计意图：引导学生思考“需要什么？”激活学生的思维，迫使学生调用已有的长、正方形面积测量的数学活动经验，思考确定一个平行四边形面积的方法。

二、探究

1.研究目标。

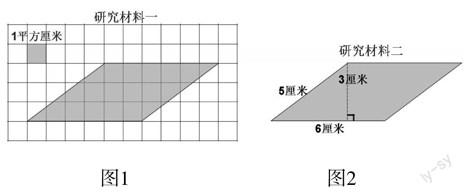
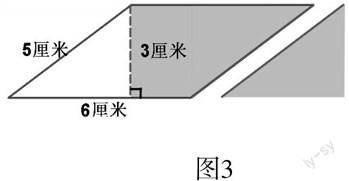
老师准备了这两种学习材料（图1、图2），请选择你需要的材料，想办法确定出图中平行四边形的面积。

图1          图2

2.反馈交流。

师：（多媒体出示图1）哪些同学是选择这个材料的？谁上来给我们介绍一下你是怎么想的？研究的结果是什么？

生1：我是这样想的，这个平行四边形的面积就是它所包含的面积单位的个数，也就是说，我们只要数出这里面有多少个面积单位就行了。我的研究结果是：它的面积是18平方厘米。

师：有同学对他的发言要提问或补充的吗？

生2：请问这里面有很多不足一个面积单位的地方，这些地方怎么数？

生1：不够一格的，我们只需要把它们拼成整格的再数就可以了。大家可以观察一下，你们看出来哪些地方可以拼在一起了吗？

生3：我发现，每一行左边的一小块都可以与它对应的右边的一块拼起来，我给大家拼一下……

（学生在多媒体课件上拖动平移）

生4：其实也可以把左边的大三角形整块移到右边拼在一起的。

……

师：这样一拼，刚才不足一格的问题解决了吗？这个平行四边形的面积是多少？若是请你写一道算式，你打算怎么写？

生5：6乘3等于18平方厘米。

师：这里的6和3分别表示什么？

生5：6表示一层有6平方厘米，3表示有这样的3层。

师：噢，用了“每层数×层数”来计算这个平行四边形所包含的面积单位的数量。

师：（多媒体出示图2）哪些同学是利用这个材料来研究平行四边形面积的？谁上来介绍一下你是怎么想的？研究的结论是什么？

生6：其实我的方法和刚才的差不多，就是把左边的三角形直接拼到右边去。不过不用数格子，拼好之后就可以看到一个长方形，这个长方形的面积就等于原来平行四边形的面积。

师：有同学对他的发言要提问或补充的吗？

生7：这个长方形的面积你是怎么知道的？

生6：我们可以看到长方形的长是6厘米、宽是3厘米，长乘宽就等于它的面积。

生8：我补充一下，其实现在看到的这个长方形的长就是原来平行四边形的底，宽就是原来平行四边形的高。

生9：这里要先明确，是沿着这条“高”剪下来的。

（交流略有停顿后教师介入。）

师：你们是先把这个平行四边形转化成一个长方形，再计算面积，对吗？那么大家想一想，一定要沿着这条高剪开吗？其他的行不行？

生10：可以的，只要是这组高都可以的。

生11：若是有数据的话，沿着另外一组高剪开拼成长方形也可以的，只是现在没数据而已。

生12：其实沿着任意一条高剪开来都可以把这个平行四边形拼成一个长方形。（教师课件演示，确实也可以。）

设计意图：我们一直在强调学习活动中学生是主体，上面的教学过程贵在放手让学生独自探究、独立思考。学生在经历自主研究后，无论目标是否实现，都会有话想说。事实上，学生讲得很好！他们在教师有意提供与搭建的分享与交流平台上，各抒己见、相互学习、各有所得。问题“一定要沿着这条高剪开吗？其他的行不行？”的设置，意在引导学生跳出现有思维，展开想象，在头脑中勾勒沿着其他的高线剪开拼组的画面，在实现方法多样化的同时，为后面讨论“任何一个平行四边形都可以通过剪拼转化成等积长方形”从而实现剪拼转化方法的“一般化”服务。

3.深入思考。

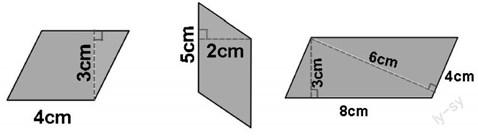
师：大家有没有想过，为什么剪、拼的时候这两条边会重合呢？（如图3）

图3

师：先把你的想法和同桌交流一下。

师：谁来和大家介绍一下你的想法？

生1：三角形的这条斜边就是原来平行四边形的边，它们一模一样的。

生2：我补充一下，这两条边是原来平行四边形的一组对边，它们是平行且相等的。

生3：这两条边的方向和长度都是一样的，当然可以重合了。

师：这个平行四边形能转化成长方形求得面积，其他平行四边形是不是都能正好拼成功？

生4：应该可以的。

师：谁能说一说其中的原因吗？

生5：随便一个什么样的平行四边形，一定有高，那么从高剪开来，因为对边平行而且相等的缘故，一定能拼成长方形。

生6：如果这个平行四边形很斜很斜的，就不一定了吧？

师：到黑板上把你想的这个平行四边形画下来给大家看一看。

（这名同学画了一个竖直方向高在图形外的平行四边形，在短暂的停顿后，学生自发地开始讨论。几分钟后，有人示意要发言。）

生7：这个平行四边形可以转化的，不过要多割几次。（学生跑上来画示意图，沿着竖直方向垂直剪下两部分，平移拼组。）

师：这个“长和宽”还是原来的“底和高”吗？

生7：还是的，不过看起来有点烦，要几段接在一起。

师：一定要这么烦吗？有没有人可以突破？

生8：不用的，这个平行四边形沿着另外一条斜斜的高剪开再拼就可以了。

设计意图：五年级学生具备一定的思辨能力，沿着高线剪开再拼的方式把平行四边形转化成等积的长方形之后，可以尝试着去思考现象背后的原因。本环节意在引导有余力的学生更深入的思考，使之明确平行四边形之所以可以转化成等积长方形求得面积，正是由平行四边形形体特征决定的。在明确原因后，利用思维的延展性，突破个例的局限性，得到等积转化对于平行四边形具有一般性的结论。

三、内化

1.计算下列平行四边形的面积。

2.反馈：面积是？你是怎么想的？

3.公式化：想一想，平行四边形的面积计算公式是什么？

设计意图：找到解决问题的方式后，照顾不同的个体，为学生提供一个自我建构的过程。引导学生调用刚刚的活动经验，解释计算过程，逐步向公式化过渡。

反思：“平行四边形的面积”是小学阶段图形测量教学中一个承上启下的内容，它上承长方形面积，下接三角形、梯形面积计算教学，一直被广大一线教师所重视和研究。但实际教学中因教具学具准备、操作活动时间限制等因素的制约，学生实际动手“剪、拼”操作的平行四边形大多是1个，准备充分的时候也只有2、3个，利用等积转化的方式推导面积公式时一般都建立在个例的操作基础上;“数格法”要么在教学中被忽略，要么以“不足一格算半格”这样生硬的规定作为解决策略，数出面积单位的个数确定面积。仔细追究，不可避免地存在某种程度的缺陷与断层。那么是否可以找到一种适合的方式弥补这一缺失呢？

上面的学习过程中，学生通过观察选择对应的两个不足一格的部分凑成一格后再数，利用数面积单位的方法确定了平行四边形的面积，避免了“不到一格算半格”的不足。其实利用数格法计算面积时，之所以可以“不足一格的算半格”正是由平行四边形的特殊性决定的，但却常常被忽略。当学生有疑问时，也经常以“看看书上是怎么处理的”一笔带过。在利用等积转化求面积的环节，以“这个平行四边形能转化成长方形求得面积，其他的平行四边形是不是都能正好拼成功？”引导学生深入思考，利用“动态想象”与“直观呈现”相结合的方法，通过激活思维实现了方法的“普适性”，弥补了实物操作的不足。

教学实践让我深深地感受到，在几何图形的教学中，我们既要重视直观操作体验，积累感性经验，还要在得到直观提示的基础上，进一步思考“如何适时适度地组织学生跨越直观操作，激活理性思维，引导学生适当的推理与数学化表达，试着解释其背后的原因”。尽管有时学生还不能够完全解释得清楚，但是坚持这样做，对于弥补直观操作的不足、培养和发展学生的逻辑思维能力，以及后续进一步的数学学习，一定会大有裨益！

◇责任编辑：徐新亮◇