水下悬浮隧道锚索稳定性分析

苏志彬，孙胜男

(聊城大学 建筑工程学院，山东 聊城 252059)

水下悬浮隧道锚索稳定性分析

苏志彬，孙胜男

(聊城大学 建筑工程学院，山东 聊城 252059)

为研究水下悬浮隧道锚索的稳定性，建立锚索在涡街激励作用下振动的数学方程，采用伽辽金法对其进行化简，锚索振动的稳定性通过Lyapunov指数法进行判断，分析了锚索动静张力比的大小、悬浮隧道系统的阻尼比和锚索参数激励频率对锚索振动稳定性的影响。计算结果表明，锚索振动失稳的范围取决于锚索的动静张力比、锚索的阻尼比和频率比(锚索参数激励频率与锚索1阶模态固有频率的比值)；当频率比为1和2左右时，随着锚索动静张力比的增大和阻尼比的减小，锚索逐渐从稳定状态转变为不稳定状态，且锚索的不稳定区域逐渐增大。

海洋工程；悬浮隧道；锚索；振动；稳定性

一种合适的跨越深水水域的系统，能够给水域两岸带来极大的经济效益。在我国，以何种方式跨越琼州海峡、渤海海峡一直是研究人员关注的焦点问题，专家学者们都在寻找一种更安全、更有效、与环境更为协调的跨越系统[1-2]。水下悬浮隧道(亦称作“阿基米德桥”)就是这样一种跨越水域的新型结构形式。这种结构形式可跨越不同类型的水域，如湖泊、海峡、河流、海湾等，且在改善交通状况的同时，对周围环境的影响十分有限，不会破坏建造地点的自然景观及产生视觉上的污染。此外，悬浮隧道还可全天候运营，并与航道互不干扰。因此，自从这种结构形式出现以来，这种跨越水域的创新方式引起了国内外专家的广泛关注[3-5]。

水下悬浮隧道锚索作为悬浮隧道的关键受荷构件，具有柔度大、质量轻、阻尼小等特点，在外激励作用下极易产生振动，因此许多专家对锚索的振动问题进行了研究。项贻强等[6]利用哈密顿原理，考虑悬浮隧道管体和锚索的耦合作用，建立管体-锚索耦合系统的振动方程，对五种典型工况的管体跨中和锚索跨中位移时程曲线进行了分析比较。葛斐等[7]建立了水下悬浮隧道锚索在波流场中顺流向涡激振动的数学方程。罗刚等[8]考虑流体-结构耦合作用和锚索的几何非线性特性，建立了锚索的非线性振动方程，并通过软件的二次开发，分析了悬浮隧道锚索在横向升力作用下的动力特点。葛斐等[9]通过哈密顿原理推导出了水下悬浮隧道锚索和管体的运动控制方程，方程中引入了锚索横向和轴向变形间的耦合效应，并在时域内对运动控制方程进行求解分析。孙胜男等[10]建立了悬浮隧道锚索非线性随机振动方程，通过蒙特卡罗数值模拟法对随机激励作用下锚索的振动响应进行了计算分析。

为研究锚索在海流作用下的稳定性问题，将隧道管体对锚索的作用简化为轴向参数激励，建立了索端参数激励作用下悬浮隧道锚索的非线性振动方程，采用Lyapunov指数意义下的振动稳定性分析方法，通过对系统最大Lyapunov指数的求解，对锚索的振动稳定性进行了分析。

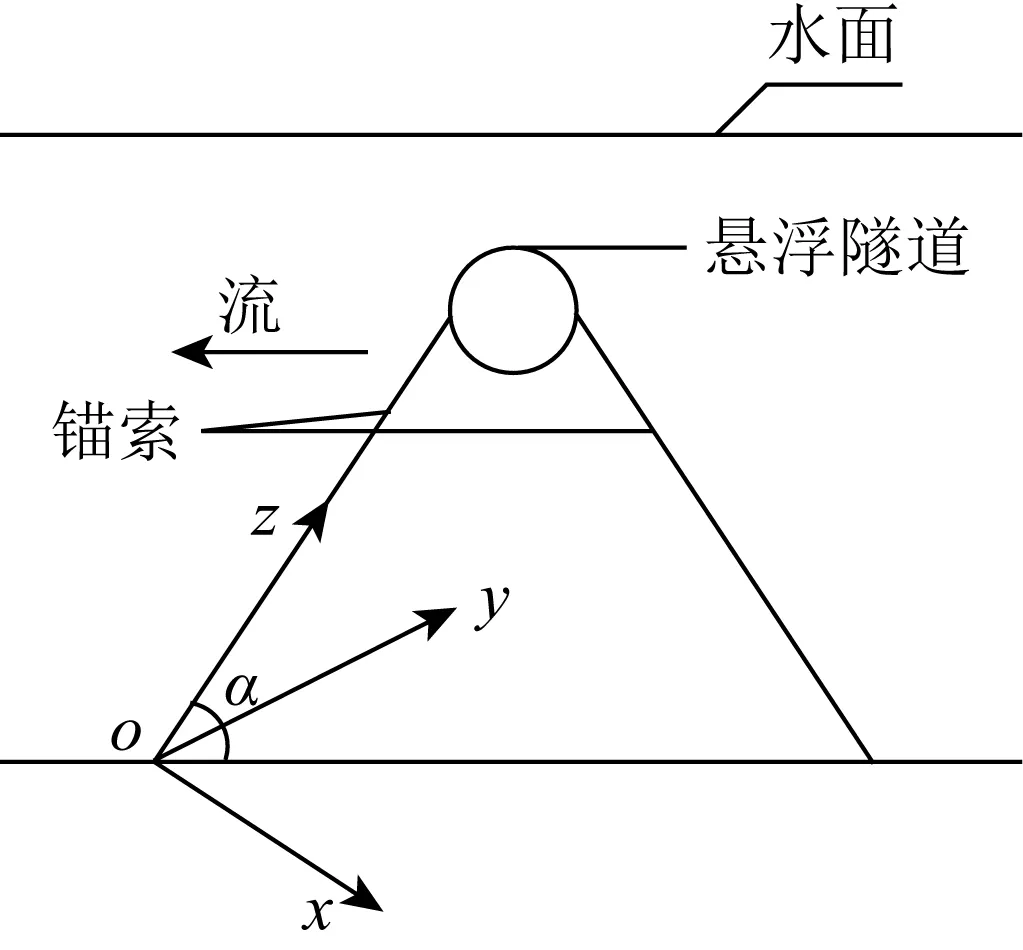
图1 悬浮隧道结构示意Fig. 1 Diagrammatic sketch of submerged floating tunnel

1 锚索振动方程的建立

建立如图1所示坐标系，其中oz轴与水底平面的夹角是α，z向沿锚索长度方向，x向在oxz平面内垂直于z向，oxz平面垂直于隧道管体长度方向，y向垂直于oxz平面。为简化模型便于计算，引入如下假设：

1)锚索位于水面30 m深度以下，可忽略波浪的影响，只考虑流的作用，且流为均匀流[11]。

2)锚索初始张拉力远远大于其自身重力，忽略拉力沿长度方向的改变。

3)隧道管体振动对锚索的影响简化为参数激励。

根据哈密顿原理可得锚索横向振动微分方程为[11]：

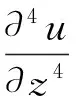
将锚索视为两端简支的结构，采用分离变量法，可得锚索横向位移u(z,t)的级数形式：

式中：l为锚索长度；N为阶数。

将式(2)～(6)代入运动方程(1)，用伽辽金法化简并取一阶模态整理得：

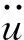
2 锚索的稳定性分析

振动系统的稳定性可以采用求解平稳状态的奇点特性来判断，这种方法为确定性非线性系统稳定性分析的标准方法；另一种方法为在原平衡微分方程上施加微小摄动来分析，此种方法结合Lyapunov指数特性，可以求解确定性系统，也可以求解随机振动系统的稳定性[12]。采用在原平衡微分方程上施加微小摄动来分析系统的稳定性，结合Lyapunov指数特性，对一微小的摄动如果无摄动运动与摄动运动非常接近，则运动是稳定的；否则，运动为不稳定。Lyaponov指数是相空间相邻轨迹发散或收敛的平均指数度量，它们表示任意动态过程的稳定特性。最大的Lyaponov指数LE1决定了过程的稳定性，当LE1<0时过程稳定，否则为不稳定[13]。

3 数值分析与结果

锚索基本参数参考国外拟建悬浮隧道[14]的设计参数，具体取值如表1所示。

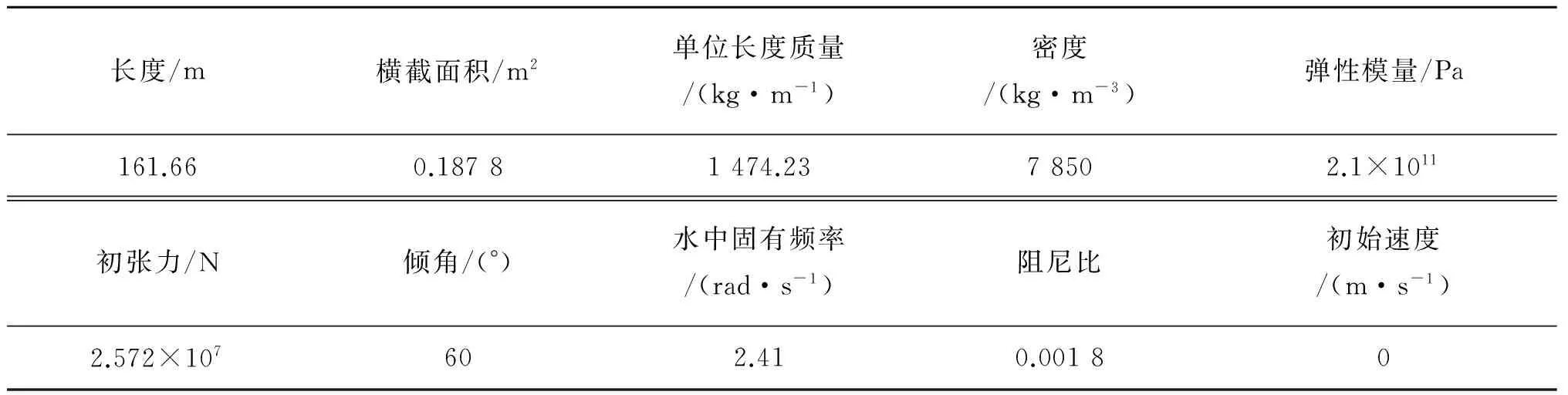
表1 基本参数Tab. 1 Basic parameters

根据Wolf[15]关于LE1的数学求解方法，采用MATLAB编制程序对Lyapunov指数进行求解，为消除瞬态振动对求解结果的影响，前100 s的数据不予考虑，其求解迭代图见图2所示。

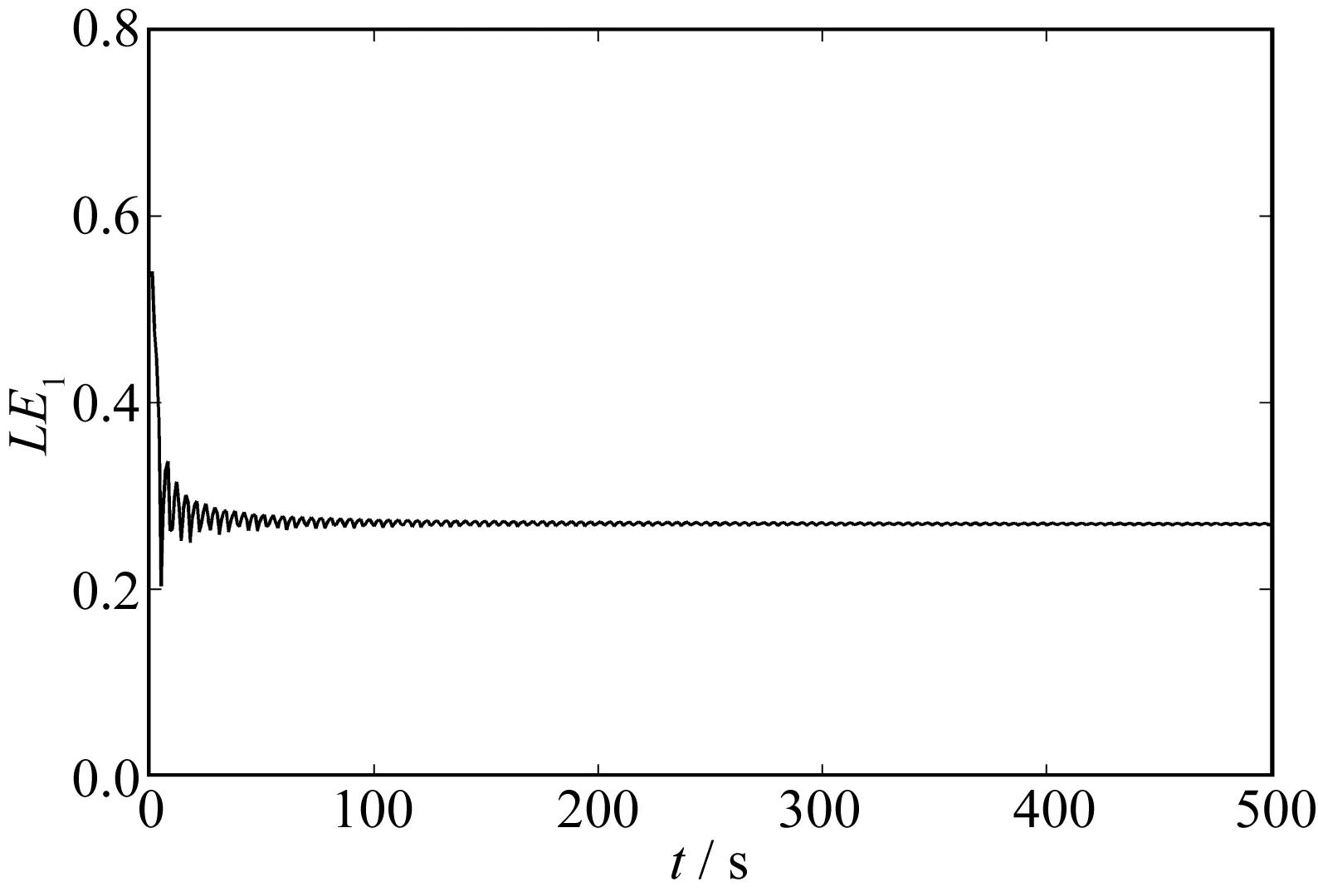
图2 Lyapunov指数求解图Fig. 2 Lyapunov exponent solving graph

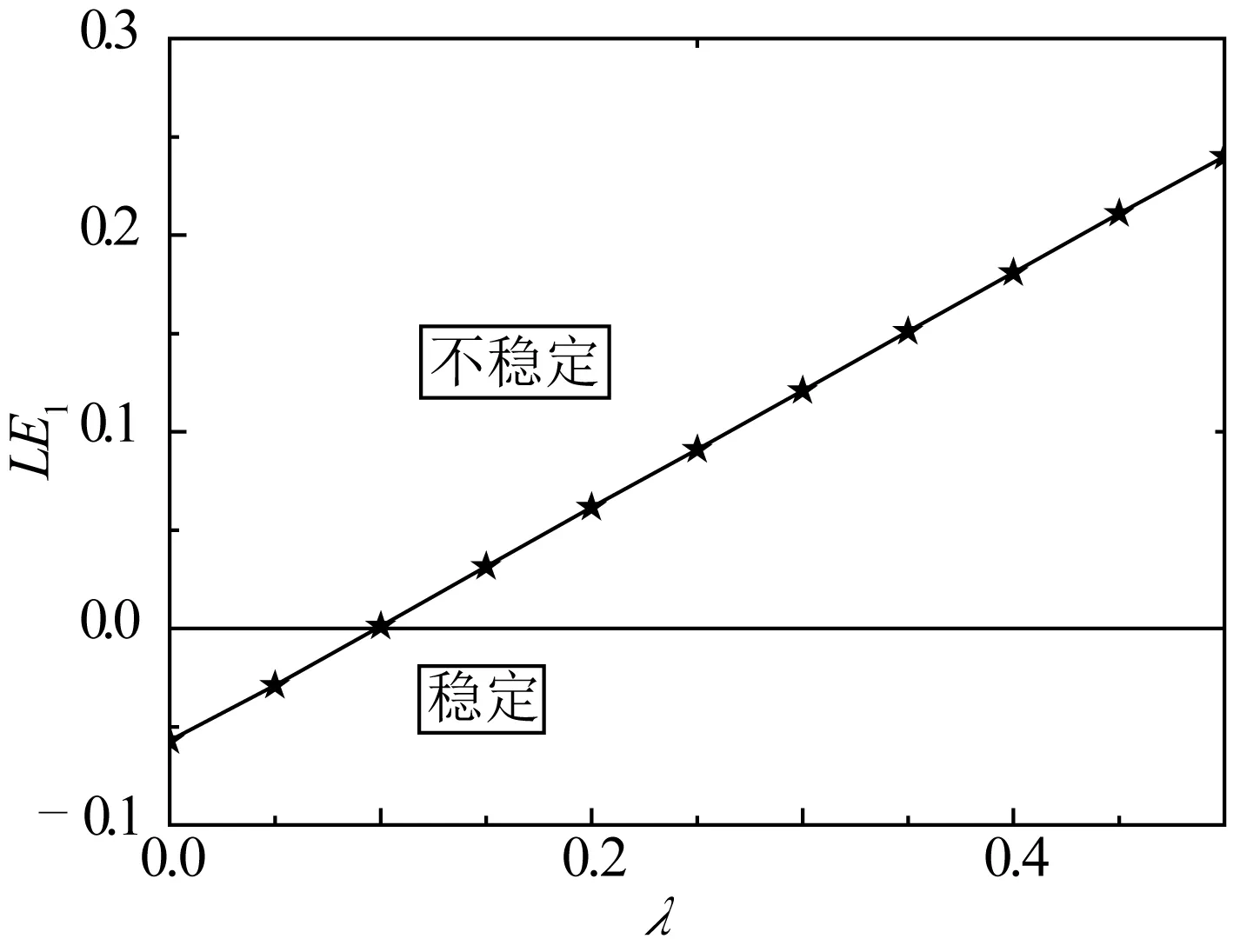
图3 锚索动静张力比和锚索稳定性的关系Fig. 3 Relationship between dynamic and static tension ratio and stability of tether

3.1动静张力比λ对锚索稳定性的影响

计算时取锚索参数激励频率与锚索1阶模态固有频率的比值(即频率比，下同)为2，则动静张力比对锚索稳定性的影响如图3所示。

由图3可见，随着锚索动静张力比的增大，锚索的振动状态逐渐从稳定转变为不稳定。锚索从稳定状态转变为不稳定状态对应的锚索动静张力比为0.1。因此，锚索的动静张力比对锚索的稳定性影响较大，且随着锚索动静张力比的增大，锚索逐渐趋于不稳定状态。

3.2锚索阻尼比对锚索振动稳定性的影响

计算时取频率比为2，计算了锚索动静张力比分别为0.25、0.30和0.35三种情况下阻尼比的变化对锚索振动稳定性的影响，如图4所示。

由图4可见，随着锚索阻尼比的增大，锚索逐渐从不稳定状态转变为稳定状态。随着锚索动静张力比逐渐增大，若要使锚索处于稳定状态，系统需要具有更大的阻尼比。

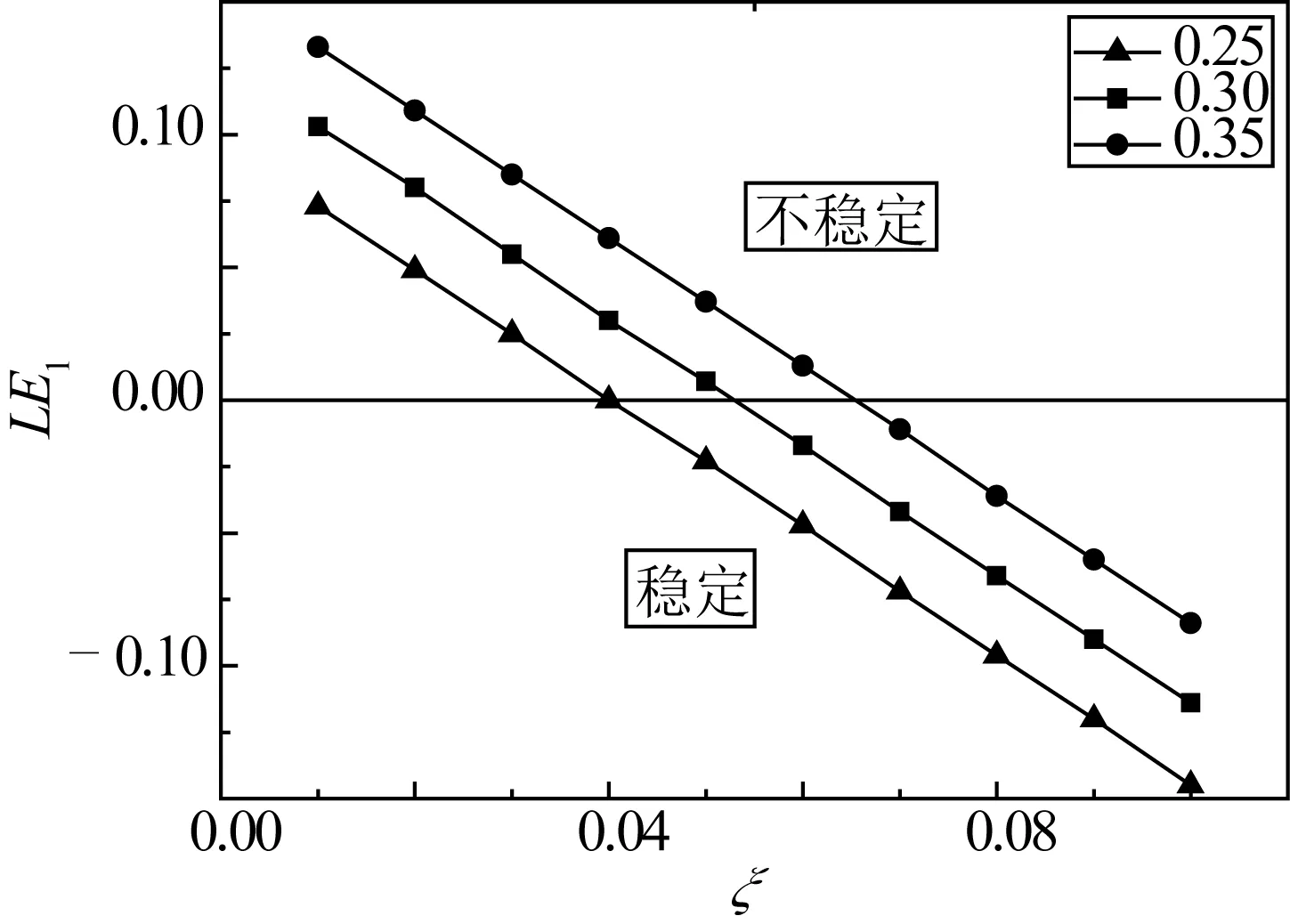
图4 阻尼比和锚索稳定性的关系Fig. 4 Relationship between damping ratio and stability of tether

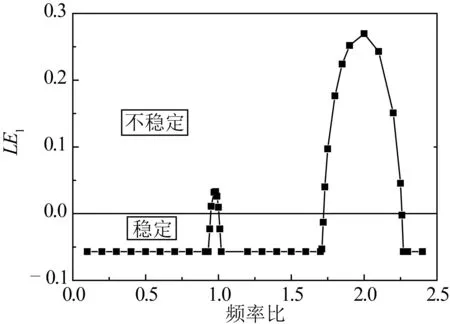
图5 频率比对Lyaponov指数的影响Fig. 5 Effect of frequency ratio on Lyaponov exponent

3.3锚索参数激励频率对其振动稳定性的影响

取锚索的动静张力比为0.55，得到锚索参数激励频率对锚索振动稳定性的影响如图5所示。

由图5可见，当锚索参数激励频率ωs在0.95ω1～1.0ω1区间和1.73ω1～2.25ω1区间范围内时，LE1均大于零，此时锚索处于不稳定状态。由此可见，锚索振动失稳状态与频率比有关。当频率比为1和2左右时，锚索极易发生失稳。

3.4锚索的稳定区域和不稳定区域

不同动静张力比和频率比情况下，锚索的稳定区域和不稳定区域如图6所示。

由图6可见，频率比在1和2附近时，随着锚索动静张力比的增加，锚索振动的不稳定区域逐渐增大。

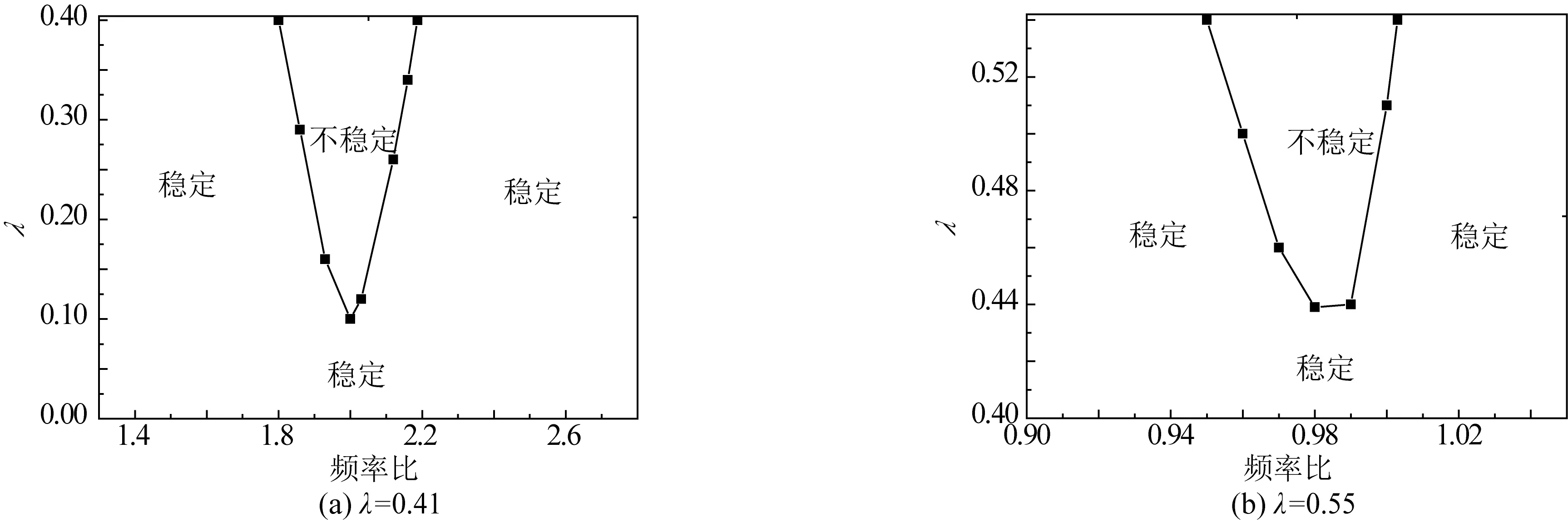
图6 不同动静张力比和频率比的稳定区域和不稳定区域Fig. 6 Stable region and unstable region of different dynamic and static tension ratios and frequency ratios

不同阻尼比和频率比情况下，锚索的稳定区域和不稳定区域如图7所示。其中，图7(a)中锚索的动静张力比取为0.41，图7(b)中锚索的动静张力比取为0.55。由图7可见，锚索在频率比为1和2附近时，随着锚索阻尼比的减小，锚索振动的不稳定区域逐渐增大。

图7 不同阻尼比和频率比的稳定区和不稳定区Fig. 7 Stable region and unstable region of different damping ratios and frequency ratios

4 结 语

锚索振动失稳的范围取决于锚索的动静张力比、阻尼比和频率比。当频率比为1和2左右时，随着锚索动静张力比的增大和阻尼比的减小，锚索逐渐从稳定状态转变为不稳定状态，且锚索的不稳定区域逐渐增大。

[1] 麦继婷, 关宝树. 琼州海峡悬浮隧道的可行性研究 [J]. 铁道工程学报, 2003, 12(4): 93-96.(MAI Jiting, GUAN Baoshu. A feasibility study on Qiongzhou Strait submerged floating tunnel [J]. Journal of Railway Engineering Society, 2003, 12(4): 93-96. (in Chinese))

[2] 宋克志, 王梦恕. 烟大渤海海峡隧道的可行性研究探讨 [J]. 现代隧道技术, 2006, 43(6): 1-8.(SONG Kezhi, WANG Mengshu. Feasibility study on Bohai Channel tunnel connecting Yantai and Dalian [J]. Modern Tunnelling Technology, 2006, 43(6): 1-8. (in Chinese))

[3] LU Wei, GE Fei, WANG Lei, et al. On the slack phenomena and snap force in tethers of submerged floating tunnels [J]. Marine Structures, 2011, 24: 358-376.

[4] WU Xiaodong, GE Fei, HONG Youshi. Effect of traveling wave on vortex-induced vibrations of submerged floating tunnel tethers [J]. Procedia Engineering, 2010(4): 153-160.

[5] FELCH J. The seattle-bellevue loop with still-water submerged floating tunnel [C]// Proceedings of the 3rd International Conference on Strant Crossing. 2001: 581-590.

[6] 项贻强, 晁春峰. 悬浮隧道管体及锚索耦合作用的涡激动力响应[J]. 浙江大学学报, 2012, 46(3): 409-415.(XIANG Yiqiang, CHAO Chunfeng. Vortex-induced dynamic response for combined action of tube and cable of submerged floating tunnel [J]. Journal of Zhejiang University, 2012, 46(3): 409-415. (in Chinese))

[7] 葛斐，董满生，惠磊, 等. 水中悬浮隧道锚索在波流场中的涡激动力响应 [J]. 工程力学，2006，23(S1): 217-221. (GE Fei, DONG Mansheng, HUI Lei, et al. Vortex-induced vibration of submerged floating tunnel tethers under wave and current effects [J]. Engineering Mechanics, 2006，23(S1): 217-221. (in Chinese))

[8] 罗刚, 石研玉, 申奇, 等. 水中悬浮隧道锚索横向动力特性分析[J]. 长安大学学报, 2012, 32(3): 73-78.(LUO Gang, SHI Yanyu, SHEN Qi, et al. Lateral dynamic characteristics analysis for cable of submerged floating tunnel in water [J]. Journal of Chang’an University, 2012, 32(3): 73-78. (in Chinese))

[9] 葛斐, 龙旭, 王雷, 等. 水中悬浮隧道管段锚索耦合模型涡激振动研究[J]. 中国公路学报, 2009, 22(3): 83-88.(GE Fei, LONG Xu, WANG Lei, et al. Study of vortex-induced vibration of submerged floating tunnel tube-tether coupled model [J]. China Journal of Highway and Transport, 2009, 22(3): 83-88. (in Chinese))

[10] 孙胜男,苏志彬. 随机激励作用下悬浮隧道锚索的振动响应 [J]. 工程力学, 2013, 30(3): 476-480.(SUN Shengnan, SU Zhibin. Vibration response of submerged floating tunnel tether subjected to random excitation [J]. Engineering Mechanics, 2013, 30(3): 476-480. (in Chinese))

[11] 陈健云, 王变革, 孙胜男.悬浮隧道锚索的涡激动力响应分析 [J]. 工程力学, 2007, 24(10): 186-192.(CHEN Jianyun, WANG Biange, SUN Shengnan. Analysis of vortex-induced dynamic response for the cable of submerged floating tunnel [J]. Engineering Mechanics, 2007, 24(10): 186-192. (in Chinese))

[12] XIA Yong, FUJION Y. Auto-parametric vibration of a cable stayed-beam structure under random excitation [J]. Journal of Engineering Mechanics, 2006(5): 279-286.

[13] 宋军伟, 方坤河. 应用Lyapunov指数研究混凝土阶段特征的稳定判据 [J]. 重庆建筑大学学报, 2008, 30(3): 129-133.(SONG Junwei, FANG Kunhe. Research on stability criterion of concrete feature in different stress stage with Lyapunov Exponent [J]. Journal of Chongqing Jianzhu University, 2008, 30(3): 129-133. (in Chinese))

[14] FAGGIANO B, LANDOLFO R, MAZZOLANI F M. Design and modelling aspects concerning the submerged floating tunnels: an application to the Messina strait crossing [C]//Prceedings of the 3rd International Conference on Strait Crossing. 2001:1-5.

[15] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317.

Stability analysis of submerged floating tunnel tether

SU Zhibin， SUN Shengnan

(School of Architecture & Civil Engineering, Liaocheng University, Liaocheng 252059, China)

To study the stability of submerged floating tunnel tether, the vortex-induced vibration equation of tether is set up, which is simplified by Galerkin method. The stability of tether vibration is judged by Lyapunov exponent method. Effects of dynamic and static tension ratio, damping ratio and parametric excitation frequency of tether on its vibration stability are analyzed. The results show that the stability of submerged floating tunnel tether depends on dynamic and static tension ratio, damping ratio of tether and frequency ratio (the ratio of parametric excitation frequency and the first order modal frequency of tether); when the frequency ratio is around 1 and 2, with the increasing of dynamic and static tension ratio and decreasing of damping ratio, the tether changes gradually from stable state to instable state and the instable region of tether increases gradually.

ocean engineering; submerged floating tunnel; tether; vibration; stability

U459.5

A

10.16483/j.issn.1005-9865.2015.01.015

1005-9865(2015)01-0119-06

2013-10-31

国家自然科学基金资助(51108224)；山东省自然科学基金资助项目(ZR2013EEL006)

作者介绍：苏志彬(1980-)，男，河北景县人，硕士，讲师，从事悬浮隧道动力响应研究。E-mail: suzhibin@126.com

孙胜男(1982-)，女，山东莱阳人，博士，副教授，硕士生导师，从事悬浮隧道动力响应研究。

E-mail: sunshengnan1982@163.com