对以正态分布法计算医疗器械抽样数量的探索

北京市医疗器械技术审评中心（100061）张高亮 吴楠 于泳

（接7月下）

设医疗器械产品数据正态分布长度为L；为了减小误差，x(i)取区间为-3σ＜X≤3σ，此时P(-3σ＜X≤3σ)=99.7%，i=8；L=6σ。

对医疗器械产品数据正态分布长度为L进行等间距分配，分为i等分，每等长度为D，确定D(0)至D(i)，然后求相临两D(i)点间对应概率。当D=L/i，i=8，D=3σ/4时计算数值如下表。见附表4。

根据正态分布图性质可知区间概率左右对称，中间数值为最大，左右依次减小。对各类医疗器械产品不合格相对率和区间概率进行排序。并对比输入各类医疗器械产品不合格相对率I(i)和输出各类医疗器械产品不合格相对率分布概率W(i)，我们整理出对称法输入I(i)和输出W(i)对比关系表见附表5。

卫生材料的不合格相对率排序1号，输入风险9.86%，对应的输出W(i)值与其他的不合格相对率排序2号，输入风险7.63%，对应的输出W(i)值均为27.36%，但是根据实际工作，卫生材料的W(i)值应大于其他的W(i)值。此误差的产生与同时与函数的本身的对称性有关，也与样本个数有关，样本个数越小误差越大。

附表6 μ=0时排序原函数法计算表

附表7 排序法输入l(i)和输出W(i)对比关系表

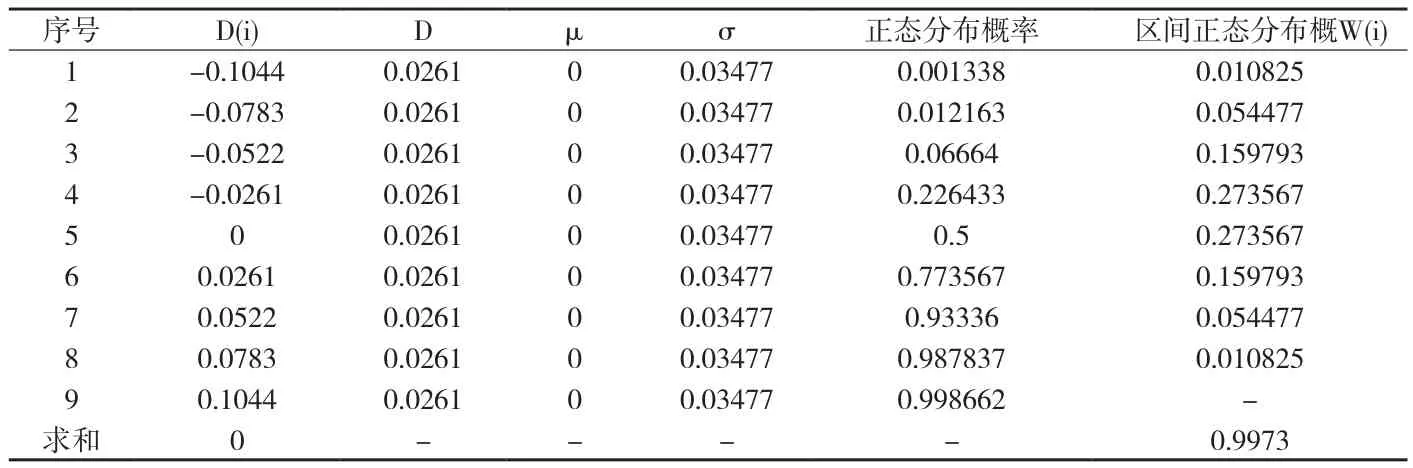
附表4 μ=0时对称原函数法计算表

附表5 对称法输入l(i)和输出W(i)对比关系表

2.4.2 排序法计算医疗器械不合格产品概率 基本思路：首先确定医疗器械产品数据正态分布区间范围长度，然后计算各序列区间内分布概率，最后确定各类医疗器械和概率之间一一对应关系。与对称法主要：区间范围不同，排序法区间范围为对称法的1/2，计算序列的概率的方法不同，排序法计算出的概率需乘以2倍。

此时区间范围为D=L/2=3σ，因正态分布以μ=0对称，左右面积值均为1/2，故计算出f(x)后再乘以2进行倍增，总面积仍然为1。进行计算得列表见附表6

2.4.3 对比排序法和对称法计算医疗器械不合格产品概率 根据附表6我们整理出对称法输入I(i)和对称法排序法输出W(i)对比关系见附表7。

由附表7可知，采用排序法消除了因正态分布对称性产生的对称误差，对数值进行优化，更加符合实际情况，优化后的数据已经不满足原始数据正态分布。

2.5 计算各类医疗器械产品抽样比例和数量 我们已计算出各个分类所对应的正态分布概率W(i)，然后计算得各类医疗器械产品抽验数量Y(i)。

根据附表7的计算结果以及上述公式关系计算医疗器械产品抽样计算相关数值见附表8。

通过以上分析获得i=8时，各类医疗器械产品最优抽样数量见附表9。

由附表9可以看出，经过正态分布计算的抽样数量与随机方法计算的抽样数量相差88个产品，占总抽样数量的21.78%。采用正态分布计算抽样数量，得出更为科学数值化的抽样比例和数量，可以更加精确、高效的开展抽样工作。

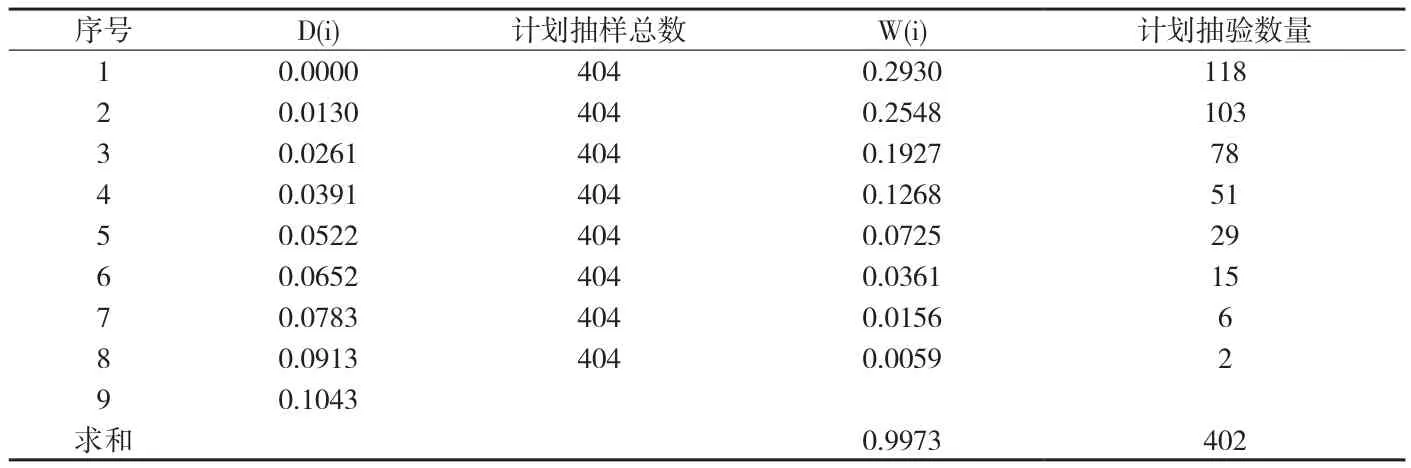
附表8 医疗器械产品抽样计算相关数值

附表9 输入抽验数量和输出抽验数量关系表

3 医疗器械抽样正态分布计算法的讨论

本文是以北京市医疗器械检验所基础数据，演示以正态分布法计算医疗器械质量监督抽样数量的方法，计算出的各分类的概率与各类医疗器械抽样不合格相对率大小一一对应。正态分布计算法为计算抽样数量的方法之一，除此之外还有随机函数法、相关性函数法等计算方法。本计算方法更加适用于抽样分类较多时的抽样数量计算，当抽样数量足够大时，采用国家局分类目录方法更有实际意义。