基于分形维数理论的海岸线遥感分类与变迁研究＊

马小峰，邹亚荣，刘善伟

（1．国家卫星海洋应用中心 北京 100081；2．中国石油大学（华东） 青岛 266580）

分形是指事物的形状、形态与组织的分解、分割、分裂与分析，它在一定程度上代表了一个由局部到整体的对事物的认识过程，而分形维数则是用来描述分形不规则特征的参数［1］。由于不同类型海岸线的形成机理不同，所以，它们在遥感影像上的形态也各不相同。根据分形维数理论，在测量方式确定的条件下，平面线状目标的分形维数越大，说明其形状越复杂，反之亦然［2－3］。具体到海岸线来说，就是海岸线的分形维数与海岸线的曲折程度存在互为正相关关系，据此，可将遥感技术与分形维数理论结合用于研究不同类型的海岸线及其变化规律。

1 我国的典型海岸线及其判定依据

根据“908专项”对我国海岸线（不包括海岛岸线）调查的结果，人工岸线约占海岸线总长度的一半以上，基岩岸线约占海岸线总长度的20%，砂质岸线约占海岸线总长度的15%，此三类海岸线的总长度已经占我国海岸线总长度的90%以上，因此，本研究选择这3种典型海岸线作为研究对象。

本研究中的海岸线测定参照《第二次全国土地调查技术规程》、“908专项”《海岸带调查技术规程》与《海岛海岸带卫星遥感调查技术规程》中关海陆分界线划分的原则进行，同时，结合以往海岸带遥感调查和现场实测海岸线工作的经验，作为对遥感影像中的我国主要类型海岸线的判定依据。

（1）人工岸线：人工海岸种类较多，最常见的是养殖场、盐田和港口码头。养殖场和盐田在遥感影像上的纹理均为网格状，这些网格即为养殖场的堤坝，可以将这些堤坝向海一侧边缘作为海岸线；港口码头由水泥和石块构筑，在近红外波段的遥感影像上具有较高的光谱反射率，与图像中的海水区分明显，可以将这种色调反差最大的边缘作为海岸线［4］。

（2）基岩岸线：基岩海岸的遥感反射率相对于海水较大，与周围海水的蓝黑色对比明显，海水潮汐变化对基岩海岸线影响较小，因此，可利用遥感影像中海陆色调反差最大的边缘作为海岸线［5］。

（3）砂质岸线：砂质海滩在图像上亮度较高，而海水在大潮时刻不能达到的地物相对亮度较低，由于砂粒是在海浪作用下冲积形成的，因此，可在遥感影像上将砂质海滩和陆地上非砂质地物的分界线作为海岸线［6］。

2 典型海岸线的分形维数分析

2．1 计算方法

采用网格法来对海岸线的分形维数进行计算［7］。网格法是使用不同长度的正方形网格连续且不重叠的覆盖被测的线状信息，当网格长度r发生变化，则覆盖线状信息所需要的网格数目N（r）也会发生变化，根据分形维数理论可得出关系

对该式两边同取对数可得

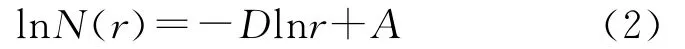
式中：A为待定常数；D为被测线状信息的分形维数［1，8］。

根据网格法的要求，选取8个网格长度指标作为覆盖海岸线网格的长度，这8个网格长度分别为20m、30m、40m、50m、60m、70m、80m和90m。对于网格数目，我们利用了数字图像中矢量图像与栅格图像的特性，通过ArcMap软件ToolBox的矢量图像转栅格图像的功能，对以上8个网格长度指标的网格数目进行统计。通过上述方法得出的网格长度r与网格数目N（r）可得出二者之间的双对数散点图，再根据最小二乘法对图中的散点进行回归分析，可拟合出线状信息的分形维数关系式［9］（图1）。

图1 分形维数关系式拟合

2．2 抽样结果与分析

选取我国辽东半岛的人工岸线、山东半岛的基岩岸线和海南的砂质岸线进行分析，海岸线提取以Landsat8卫星30m分辨率的多光谱数据和15m分辨率的全色波段数据进行融合的影像作为数据源，采用数字图像边缘检测［10］和人工目视解译相结合的方法。为了尽可能减少对多时相遥感影像人工目视解译过程中出现的人为判定误差，海岸线提取除必须满足前面的海岸线判定依据以外，我们将所有同为15m分辨率的遥感影像调配至1∶50 000的比例尺进行海岸线提取。经网格法对选取的海岸线的分形维数D及网格长度r与网格数目N（r）的相关系数进行计算，得出结果如表1、表2和表3所示。

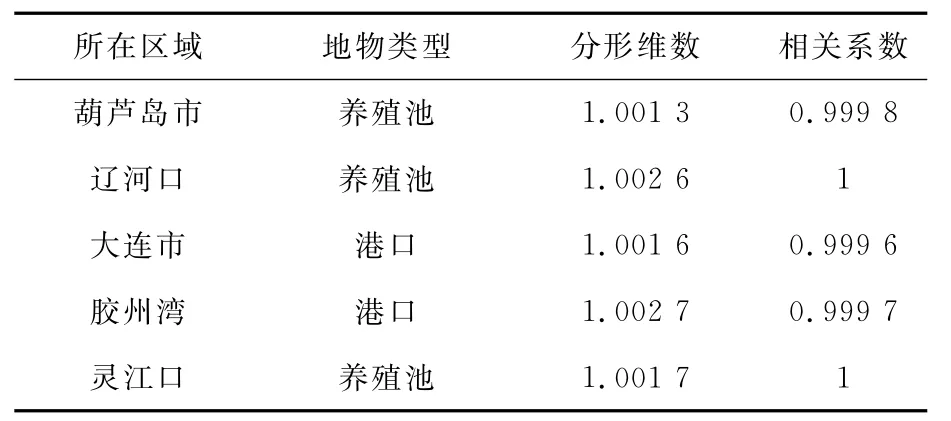
表1 人工岸线分形维数

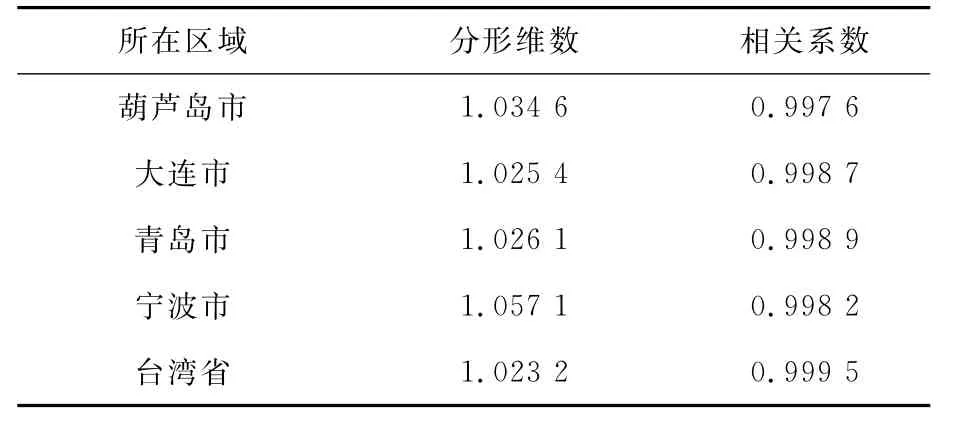
表2 基岩岸线分形维数

表3 砂质岸线分形维数

通过对3种类型海岸线分形维数的计算可以看出，基岩岸线的分形维数相对较大，人工岸线次之，砂质岸线分形维数相对最小。根据分形维数理论，平面线状目标的分形维数在1～2之间，即1＜D＜2。取海岸线分形维数的有效部分（D－1）进行比较，如图2所示，3种类型海岸线分形维数有效部分的数量级不同，但相同类型海岸线的分形维数都在固定的数量级范围内变化。

图2 海岸线分形维数对比

基岩海岸主要由花岗岩、玄武岩和石英岩等坚硬的岩石构成，受海浪反复撞击冲刷以及海水对海岸溶蚀等自然界随机风化作用的影响，形成了基岩岸线较为曲折的不规则形态，故而其分形维数较大；人工海岸是人类为满足生产需要而修建的建筑物，形状较为规则，虽然受海岸地形限制和建筑物功能要求，人工岸线总体上有一定的曲折程度，但在小范围长度上仍是规则的直线形状，故其分形维数相对曲折的基岩岸线来说较小；砂质海岸是海底岩石风化和被河流带进海洋的石英砂在海浪的冲击磨洗下形成微小颗粒后，堆积在平缓的海岸而形成的，由于形成砂质海岸的岸坡较为平缓，且经过长年的积累，因此，砂质岸线较为平滑，虽不能完全形成直线，但没有明显的凹凸之处，故其分形维数最小［11］。

3 海岸线变迁状况的分形维数规律

不仅不同类型海岸线的分形维数有各自的特点，而且固定区域海岸线的分形维数变化也有一定规律。本研究选取辽宁省辽东半岛的大连市的部分海岸带（东起大连市与丹东市的分界线，西至大连港）作为研究对象，在自然条件下，该区域主要为基岩海岸，经过多年开发后出现很多海港和养殖区，目前，该区域以基岩海岸和人工海岸为主。

选取研究区内海岸线变化较明显的遥感影像进行比对可以看出，在研究区海岸线由基岩海岸被开发为人工海岸的过程中，海岸线的曲折程度下降幅度较大，其形状趋于规则平直，而原有的人工海岸被修缮后，其曲折程度也有所下降，但趋势明显较为缓慢，并不明显。据此可以推断，随着海岸带开发的不断进行，海岸线的曲折程度将随着时间的推移逐渐下降。

用研究区2009年、2011年和2013年3个时相的遥感影像进行海岸线提取，使用网格法计算后得出研究区内3个不同时期的海岸线的分形维数分别为D2009＝1．064 8、D2011＝1．055 6和D2013＝1．046，如图3所示，对比2009－2013年这3个时段的海岸线分形维数可知，研究区的海岸线的曲折程度不断下降，这与上述通过遥感影像目视解译分析得出的结论相符合。根据分形维数理论可以推断，单位时间内，影响海岸线变化的海岸带开发活动越剧烈，则海岸线分形维数变化越大。

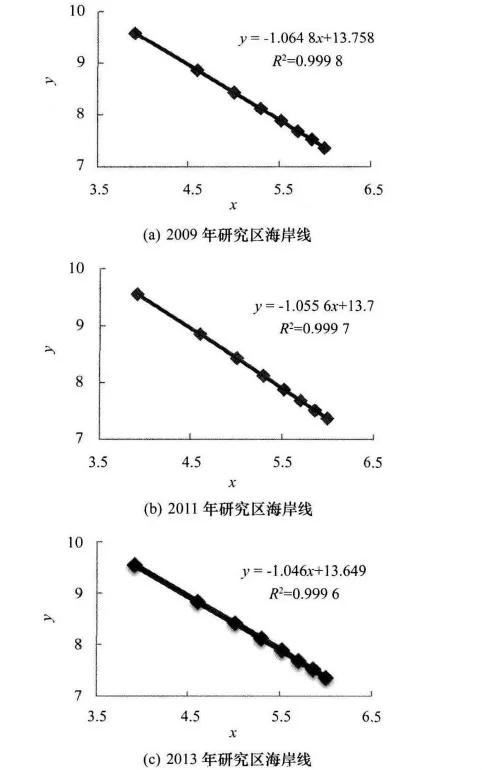
图3 研究区分形维数关系式拟合

4 海岸线分形维数理论应用的意义

以往对海岸线的分类都是以地理意义上的海岸带类型为依据，而将分形维数理论引入对海岸线的研究可以根据海岸线的曲折程度对海岸线进行分类，从而使海岸线的变化情况能够被定量描述，实现海岸线类型的数字化，拓展海岸带遥感的研究领域。同时，在以我国海岸带为研究区域的范围内，不同地物类型海岸线分形维数的有效部分（D－1）在数量级上区别较为明显，可以作为区别不同地物类型海岸线的数学特征。因此，海岸线的分形维数与海岸带的地物类型及演变过程有直接关系，具备深入应用的价值。

利用分形维数理论，即使是由多种类型地物组合而成的复合型海岸带，其海岸线变化情况也可以通过计算得出具体的数学结果，从而打破海岸线按属性分类时受海岸带类型限制的局面，使海岸线遥感研究由定性的目标识别转变为定量的数学分析。在当前我国海岸带开发的活跃时期，人工开发海岸带导致海岸线变化较为频繁，基于分形维数理论对海岸线进行分类，完全可以在海岸带遥感调查工作中把海岸线的分形维数作为衡量海岸带变化状况的直接依据，为政府的管理工作提供支撑。

［1］ 朱晓华．地理空间信息的分形与分维［M］．北京：测绘出版社，2007．

［2］ 徐进勇，张增祥，赵晓丽，等．2000－2012年中国北方海岸线时空变化分析［J］．地理学报，2013，68（5）：651－660．

［3］ 陈正华，毛志华，陈建裕．利用4期卫星资料监测1986－2009年浙江省大陆海岸线变迁［J］．遥感技术与应用，2011，26（1）：68－73．

［4］ 冯金良，郑丽．海岸线分维的地质意义浅析［J］．海洋地质与第四纪地质，1997，17（1）：45－51．

［5］ 叶小敏，纪育强，郑全安，等．胶州湾海岸线历史变迁的分形分析［J］．海洋科学进展，2009，27（4）：495－501．

［6］ 国家海洋局908专项办公室．海岛海岸带卫星遥感调查技术规程［Z］．北京：海洋出版社，2005．

［7］ 朱晓华．海岸线分维数计算方法及其比较研究［J］．黄渤海海洋，2002，20（2）：31－36．

［8］ 朱晓华，潘亚娟．GIS支持的海岸类型分形判定研究［J］．海洋通报，2002，21（2）：49－54．

［9］ 王新生，王红，朱超平．ArcGIS软件操作与应用［M］．北京：科学出版社，2010．

［10］ CANNY J．A computational approach to edge detection［J］．Pattern Analysis and Machine Intelligence，1986，8（1）：679－697．

［11］ 朱晓华．江苏淤泥质海岸海岸线分形机理研究［J］．海洋科学，2002，26（9）：70－73．