基于粗糙集与最小二乘支持向量回归的汽轮机主蒸汽流量预测
张维平,赵文蕾,李国强,牛培峰
(1.秦皇岛职业技术学院机电工程系,河北 秦皇岛 066100;2.燕山大学电气工程学院,河北 秦皇岛 066004)
基于粗糙集与最小二乘支持向量回归的汽轮机主蒸汽流量预测
张维平1,2,赵文蕾1,李国强2,牛培峰2
(1.秦皇岛职业技术学院机电工程系,河北秦皇岛066100;2.燕山大学电气工程学院,河北秦皇岛066004)
针对传统主蒸汽流量计算方法的不足,提出了一种新的主蒸汽流量预测方法,该方法综合了粗糙集理论与最小二乘支持向量回归算法的优点,利用ROSETTA V1.4.41研究实验平台中的遗传约简算法对输入变量的属性进行约简,再利用最小二乘支持向量回归算法建立主蒸汽流量的预测模型。实验表明,与未经粗糙集理论处理过的BP神经网络、支持向量回归算法和最小二乘支持向量回归算法所建模型相比,该方法具有更好的预测精度和泛化能力,且建模速度显著提高。
计量学;主蒸汽流量;滑压运行曲线;最优初压;最小二乘支持向量机;引力搜索算法
1 引言
2 基于弗留格尔公式的主蒸汽流量计算
利用调节级后压力来计算主蒸汽流量的方法是依据汽轮机变工况计算中的弗留格尔公式。对于具有n级的汽轮机组变工况运行时在未达到临界前,机组前后的参数和流量之间的关系为[6]:

式中:G为主蒸汽流量(t/h);T为级组前(后)的绝对温度(K);P为级组前(后)的绝对压力(MPa)。下标0指额定值;X指实际值;1指级组前的参数;2指级组后的参数。
当所取的机组比较多且包含凝汽式机组的末级时,因为排汽压力值要远远小于进汽压力值,所以在计算时可将排汽压力值忽略不计。此时式(1)变为:

将式(2)变形后可得到实际的主蒸汽流量GX:

目前,大多数机组的数据采集系统(DAS)中所显示的主蒸汽流量是由式(4)计算得出:

式中:K为常数,取决于系统设计时的主蒸汽流量、调节级后压力和温度等参数。然而,式(4)的计算结果也常常会产生较大的误差,文献[7]中的试验结果表明,该电厂的机组在350 MW负荷左右时,计算得到的主蒸汽流量值与实验测得的数值相差约30~40 t/h,相对误差在3%以上。分析其中的主要原因发现,一方面是现场对于没有调节级后温度测点的机组采用主蒸汽温度值来代替,而实际汽轮机组在变负荷运行时,主蒸汽温度与调节级温度之间并非一一对应的关系;另一方面,K值无法保持恒定,随着机组运行状态的改变,需要不断地修正以满足对测量精度的要求,这就给现场应用带来很大的不便。因此,建立一种方便、准确的主蒸汽流量计算模型对电厂具有重要的意义。
在进行正式开挖清淤之前,还要进行试挖,收集有关开挖的深度和尺寸等相关的数据,确保后期工作符合设计的要求。
3 基于RS-LSSVR的主蒸汽流量预测
3.1粗糙集理论
RS理论[8]通常采用信息系统或信息表的形式构成知识表达系统,可以表示为四元有序组K= (U,A,V,ρ)的形式,其中U=(x1,x2,…,xn)为论域,又称非空有限对象集;A=C∪D为非空有限属性集;C为条件属性集;D为决策属性集;V=(v1,v2,…,vm)为属性的值域;ρ:U×A→V为信息函数,反映论域U与属性集A到值域V的映射。这时的信息系统又被称作“决策表”。对于A中的任何属性子集B,在U上的等价关系可以用下式表达:

如果(x,y)∈I(B),则x,y相对于B是不可分辨的。设RB是一个等价关系簇,如果RB=RB{b},则称属性b是多余的;如果系统中不存在多余的属性,则称B是独立的;倘若RB=RA且B是独立的,则称B为A的约简;A中所有约简的交集称作A的核。
属性约简算法[9]是粗糙集理论的核心内容之一。常用的算法主要有:X.H.Hu算法、Pawlak属性重要性算法、遗传算法以及差别矩阵算法等。
3.2最小二乘支持向量机回归算法
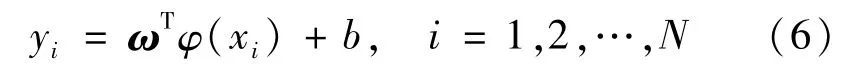
式中:ω为权重向量,b为偏置量。目标函数描述为:

式中:ei为松弛变量,γ为正则化参数。对于优化问题,引入Lagrange因子α,α∈RN×1,由KKT最优条件,式(2)的解为:
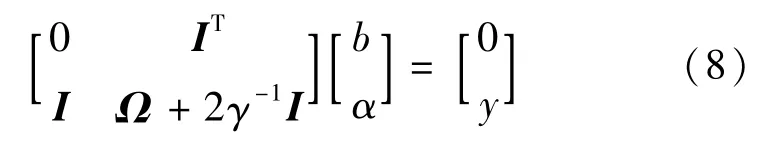
式中:y=[y1,y2,…,yN]T,I=[1,1,…,1]T,α= [α1,α2,…,αN]T,Ω为一个N×N的对称矩阵。对于式(8),令H=Ω+2γ-1I,则模型系数的解为:

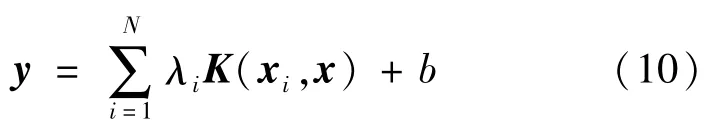

3.2RS-LSSVR模型
虽然LSSVR有良好的预测精度、泛化能力和鲁棒性,但LSSVR无法确定样本特征值中哪些有用,哪些冗余。在建模过程中,一旦样本数据的维数过高或数据量过大,其训练的复杂度就会大大增加,导致训练时间过长或者出现过拟合现象。而粗糙集理论能够通过一定的算法挖掘数据间潜在的关系,通过去除数据中冗余的信息来简化输入样本的维数,但实际应用中粗糙集方法往往对噪声非常敏感,鲁棒性差,这个缺点限制了它在工业生产中的应用范围。因此,本文结合LSSVR算法与RS属性约简方法的优点,提出了一种RS-LSSVR混合建模方法来预测汽轮机的主蒸汽流量,图1给出了RS-LSSVR混合建模的流程图。首先利用RS理论的属性约简算法对输入数据进行处理,消除冗余信息,减少输入变量的维数,构建新的训练样本与测试样本,然后再利用LSSVR算法建立主蒸汽流量的预测模型。
3.4基于RS-LSSVR的主蒸汽流量预测
本文所需样本数据来自某电厂600 MW超临界机组DCS系统中采集的现场运行数据。根据主蒸汽流量的物理特性及文献[3]中给出的相关分析,选取8个输入变量,1个输出变量,具体如表1所示。采样间隔为1 h,每天采集24组数据,确定360组样本作为训练集,72组样本作为测试集。本文所有仿真实验均在2009年版本MATLAB软件中完成,每次实验均重复30次,电脑配置为Inter(R)Core(TM)i5 2430M CPU(2.40 GHz)处理器,4.00 GB内存,Windows 7.0操作系统。

图1 RS-LSSVR混合建模流程图

表1 主蒸汽流量建模初始输入变量选择
本文利用ROSETTA V1.4.41研究实验平台,采用软件中提供的遗传约简算法来实现输入变量的属性约简。属性约简的的结果如表2所示。
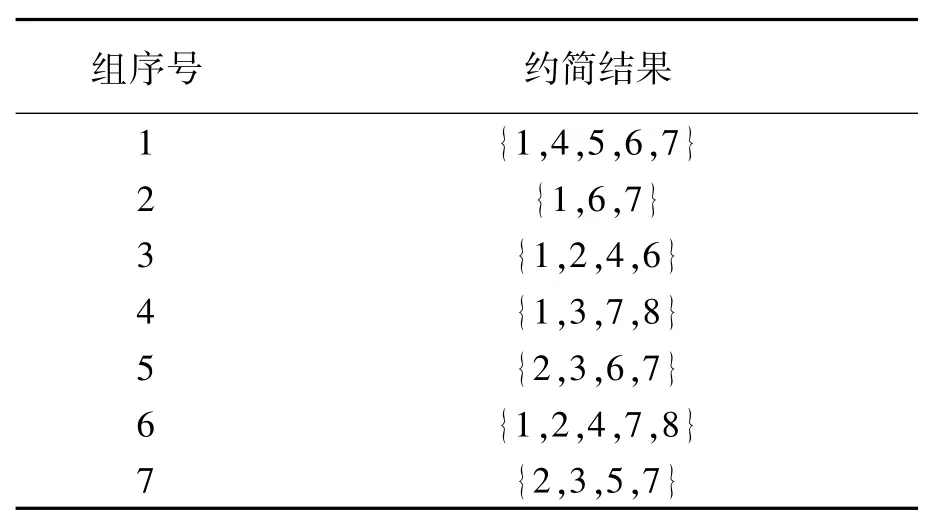
表2 约简结果
从实际情况分析,主蒸汽流量的大小主要取决于调节级压力的大小,此外还受一段抽汽压力、负荷、一段抽汽温度以及高压缸排汽压力的影响,与汽机侧的主蒸汽温度、压力或高压缸的排汽温度关系并不密切。综合考虑,本文认为第1组属性约简的结果更符合实际,约简后的输入变量维数减少至5个,分别为负荷、调节级后压力、一段抽汽温度、一段抽汽压力和高压缸排汽压力。图2给出了属性约简后的LSSVR结构图。
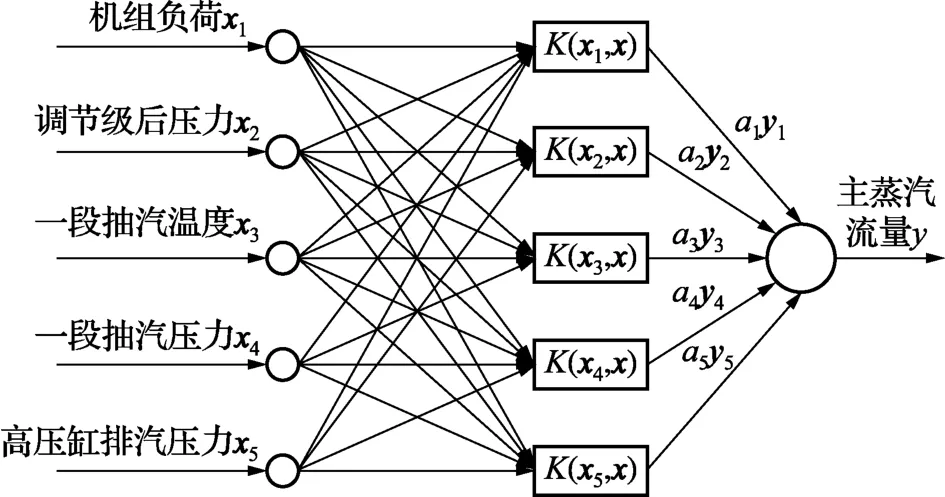
图2 属性约简后的LSSVR结构图
在利用LSSVR算法建立主蒸汽流量预测模型时,选择RBF核函数,利用网格搜索法确定模型参数,γ=892.3954,σ2=144.4721。为避免计算时溢出,所有样本数据都利用式(12)进行归一化处理。

归一化方法可有效提高算法的收敛速度、缩短模型的训练时间。经变换后,数据取值在[0,1]之间,于是得到新的时间序列xj,在建模分析之后,还需将其还原到原始区间。图3给出了基于RSLSSVR的训练集样本主蒸汽流量回归预测结果,图4给出RS-LSSVR模型对未经训练的测试集数据进行预测的结果。

图3 基于RS-LSSVR的训练集样本主蒸汽流量回归预测

图4 基于RS-LSSVR的测试集样本主蒸汽流量回归预测
从图3中不难看出,得到的预测值与实际值几乎完全相等,这表明基于RS-LSSVR的主蒸汽流量预测模型具有较高的预测精度。与此同时,从图4中可以看出,测试样本的回归精度也比较高,这表明该模型具有良好的泛化能力。由此可见,该回归模型的的预测效果能够满足工程实际需求,可对不同工况下的主蒸汽流量进行准确预测。
4 性能比较
为进一步验证RS-LSSVR模型的性能,利用未经RS处理的数据样本,通过BP、SVR和LSSVR分别进行主蒸汽流量的建模,最后对不同模型的建模效果进行比较与分析。为比较基于不同算法的主蒸汽流量预测模型的性能,选用均方根误差σRMSE和确定系数R2作为评价指标:
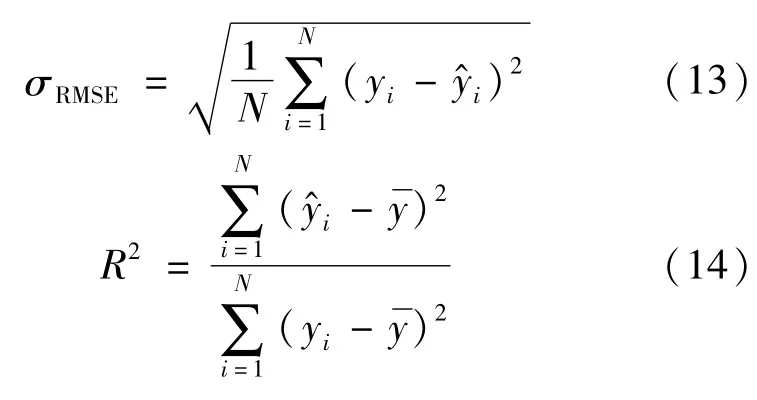
评价指标σRMSE值越小,表明预测误差越小,预测精度越高。而确定系数R2越接近于1,表明预测值与实际值的拟合精度越高,预测效果越好。
在利用BP神经网络建立主蒸汽流量的预测模型时,确定BP的结构为8-5-1,即输入层有8个节点,隐含层有5个节点,输出层有1个节点。BP网络隐含层中的神经元采用Sigmoid型变化函数,输出层则采用线性结构,输入输出数据经归一化处理后都限制在[0 1]之间,训练的相对误差目标值设为0.000 1;在利用SVR建立主蒸汽流量的预测模型时,选用RBF核函数,利用林志仁教授提出的libsvm工具箱来实现SVR的建模。此外,SVR算法的参数选择采用3阶交叉验证法来选择模型的参数,得出的结果为(c,g)=(1024,9.7651);在利用LSSVR建立主蒸汽流量的预测模型时,也选用RBF核函数,采用网格搜索法优化模型参数组合(γ,σ2),其中网格设置为γ=[2-9,2-9,…,29,210],σ2=[2-9,2-9,…,29,210],得到的结果为(γ,σ2)= (1000,144.4721)。
表3给出了基于4种建模方法的主蒸汽流量预测模型的性能评价结果。图5和图6给出了基于4种建模方法的训练集和测试集样本的主蒸汽流量回归预测误差曲线。

表3 4种建模方法性能比较

图5 基于4种建模方法的训练集主蒸汽流量回归预测误差

图6 基于4种建模方法的测试集主蒸汽流量回归预测误差
通过比较发现,4种建模方法中,BP神经网络建模的速度最快,但模型的预测精度及泛化能力却是最差的。SVR的预测效果要好于BP神经网络,但由于SVR算法本身就比LSSVR算法要复杂,再加上采用了3阶交叉验证法来确定模型的超参数,所以耗费时间最长。重点来对比一下LSSVR与RSLSSVR的建模效果,经粗糙集理论的属性约简算法处理后,输入变量的维数由原来的8个减少为5个,这使得RS-LSSVR的建模时间比LSSVR缩短了约14.41%。但是,由于采用粗糙集对输入样本空间进行特征选择时,剔除了噪声数据的影响,这使得所建模型的预测性能非但没有下降,反而有所提高。从仿真结果来看,无论是训练集还是测试集,基于RSLSSVR的主蒸汽流量回归预测误差均为最小。
5 结论
本文主要针对汽轮机的主蒸汽流量提出了一种基于RS-LSSVR混合建模的软测量方法,相比BP神经网络、标准的SVR和LSSVR的主蒸汽流量建模效果,基于RS-LSSVR的主蒸汽流量预测模型具有更高的预测精度、更好的泛化能力和更快的训练时间。同时也表明了在汽轮机主蒸汽流量建模时,输入变量的特征并非选取越多建模的效果就一定越好。
[1]吴海姬,王雷,司风琪,等.基于BP神经网络的主蒸汽流量计算模型[J].汽轮机技术,2007,49(4):269-273.
[2]王雷,张瑞青,肖增弘,等.基于SVM的主蒸汽流量回归估计[J].华东电力,2008,36(12):89-92.
[3]周建新,王雷,吴海姬,等.基于支持向量回归的大容量机组主蒸汽流量建模[J].热能动力工程,2008,23 (2):122-126.
[4]王伟,陈殿生,魏洪兴,等.装载机载重测量的支持向量机软测量建模方法[J].计量学报,2008,29(4):329 -333.
[5]陈果,周伽.小样本数据的支持向量机回归模型参数及预测区间研究[J].计量学报,2008,29(1):92-96.
[6]孙永平,朱芳梅,王敏.北仑电厂2号机组DAS系统主蒸汽流量计算模型的修改[J].浙江电力,2000,9(3):14-16.
[7]何军民,李明.湘潭电厂300MW机组主蒸汽流量计算模型的修改[J].湖南电力,2005,25(5):17-19.
[8]Zou Z H,Tseng T L,Sohn H,et al.A rough set based approachtodistributorselectioninsupplychain management[J].Expert systems with applications,2011,38(1):106-115.
[9]雷绍兰,孙才新,周兰,等.属性约简在空间负荷预测中的应用[J].重庆大学学报,2004,27(3):85-88.
[10]Sunken J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[11]Keerthi S S,Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation,2003,15(7):1667-1689.
Forecasting of Turbine Main Steam Flow Based on Rough Sets and Least Squars Support Vector Machine Regression
ZHANG Wei-ping1,2,ZHAO Wen-lei1,LI Guo-qiang2,NIU Pei-feng2
(1.Department of Electromechanical Engineering,Qinhuangdao Institute of Technology,Qinhuangdao,Hebei 066100,China;2.Institute of Electrical Engineering,Yanshan University,Qinhuangdao,Hebei 066004,China)
A new prediction method is put forward in view of the shortages of traditional main steam flow calculation method,which combines the advantages both rough set theory and least squares support vector regression algorithm.Therefore,this new method is called RS-LSSVR.In RS-LSSVR,the attributes reduction of input variable by genetic algorithm is carried out on the ROSETTA V1.4.41 research experimental platform,then the main steam flow prediction model is established by LSSVR algorithm.The simulation results show that the method based on RS-LSSVR has better prediction precision and generalization ability compared with BP algorithm,support vector regression algorithm and LSSVR algorithm without treated by the RS theory.Moreover,the modeling speed increases significantly.
Metrology;Main steam flow;Sliding pressure operation curve;Optimal initial steam pressure;Least squares support vector machine;Gravitational search algorithm
TB937
A
1000-1158(2015)01-0043-05
10.3969/j.issn.1000-1158.2015.01.10
2012-12-20;
2013-04-15
河北省自然科学基金(F2010001318)
作者简介:张维平(1980-),女,河北保定人,秦皇岛职业技术学院讲师,博士,主要从事启发式智能优化算法、热工过程控制的研究。flamelikezwp@yahoo.com.cn

