基于最小残差思想的一类代数Riccati方程的牛顿迭代求解

周立平

（湖南科技学院 理学院，湖南 永州 425199）

基于最小残差思想的一类代数Riccati方程的牛顿迭代求解

周立平

（湖南科技学院 理学院，湖南 永州 425199）

本文在牛顿迭代法框架下，借用最小残差法思想，结合预条件共轭最小二乘法，提出了一种新的算法对一类代数Riccati方程的数值解进行了研究，并给出了具体的数值算例。算例结果验证了该方法具有良好的收敛性。

代数Riccati方程（ARE）；最小残差法；Lyapunov方程；预条件共轭梯度最小二乘法（PCGLS）；牛顿迭代法

1　引 言

代数 Riccati 方程源于控制理论中的数值问题，它在非稳定系统模型降阶，线性二次校正问题和H2优化控制中有十分重要的作用。这些问题的解决在一定条件下都可以转化为求（广义）代数 Riccati方程的稳定解。本文旨在研究如下一类（广义）代数 Riccati 方程（ARE）的数值解：

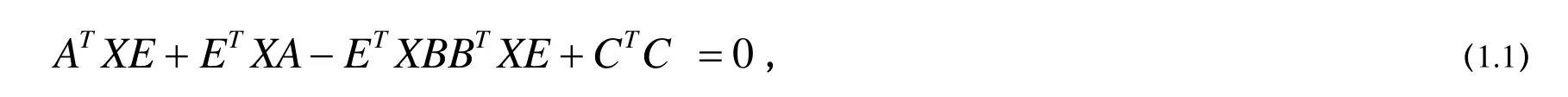
求解ARE（1.1）的直接法有schur 向量法[1]和符号函数法[2]等，它们主要是基于系数矩阵的特征分解而提出的。假设ARE（1.1）的系数矩阵具有良好的结构，如它们是低秩或稀疏的，若仍采有直接法，则系数矩矩阵的良好结构特点在计算中就被白白浪费。因此，直接法并不适合用于大规模稀疏系统的计算。由于方程（1.1）是非线性的二次矩阵方程，这使得在牛顿迭代法框架下对该类方程进行数值求解成为研究ARE求解的主流方法。

应用牛顿迭代法求解ARE，已经产生了一系列的求解解法，如Chandrasekhar迭代法[3，4]和NM-Kleinman 迭代法[5，6]等，其主要思想是将二次方程线性化后再求解。Peter Benner等人在文[7]中给出了低秩牛顿Cholesky因子法（LRCF-NM）和低秩牛顿 Galekin-ADI 方法（LRCF-NM-GP-ADI），并对 ARE方程的低秩形式解的理论也进行了讨论。

这些方法的共同关健处是求解一系列（或降阶）Lyapunov方程。这使得对方程ARE（1.1）的求解是否快速稳定主要取决于这些Lyapunov方程的求解实现。Lyapunov方程的求解一直是数值代数专家研究的热点问题，已经取得一系列研究成果[8，9]。最近，Lin与 V.Simoncini 在文[10]中提出了基于最小残差法（MINRES）求解大规模Lyapunov 方程的方法，并做了一定的理论分析，取得了很好的效果。

在文[10]的启发下，本文旨在牛顿迭代法框架下，借用最小残差法的思想，利用预条件共轭最小二乘法（PCGLS）求解Lyapunov方程，进而得到ARE（1.1）的数值逼近解。为方便起见，对将用到的符号作如下约定：表示矩阵A的Frobenius范数；I表示相应阶数的单位矩阵；若A与B为同类型实矩阵，则为定义的矩阵A与B内积。

一般说来，方程（1.1）不一定可解，即使有解也可能并不唯一。为方便研究，我们对系数矩阵给出一定的限制条件使其能具有唯一半正定解。幸运的是，许多源于实际问题的ARE 方程其系数矩阵大多也能满足该限制条件。下面的引理给出了ARE（1.1）有唯一半正定解的存在条件。

引理1.1[12]设矩阵对为可稳化的，矩阵对为可测的，则ARE（1.1）有唯一半正定解，且该解是稳定的。

2　求解ARE（1.1）的新算法

对其求Frechét导数，得到

从而，得到如下算法。

算法 2.1 （ARE-NM）

Step 3.求解Lyapunov方程的解Nl

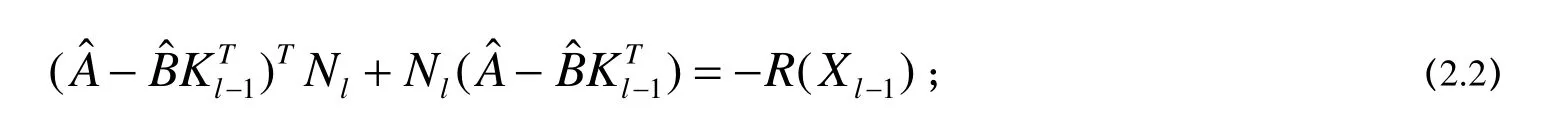
注意到算法（2.1）中需要求解一系列Lyapunov 方程（2.2），本文假设在迭代过程中始终是半正定的（这一假设在一定条件下是能成立的，可参考文[9]的第3节）。设具有分解式

得到如下一般形式的Lyapunov方程

对于方程（2.5），现在最常用的方法是投影空间方法，其思想主要是建立一个近似空间（搜索空间），利用投影算子将方程投影到该空间得到新的降阶矩阵方程，然后对其进行求解。如果得到的近似解不能达到精度，则扩充该空间，并重复上述工作直至收敛。近似空间的一种标准取法是取为Krylov 子空间，如

也可取其扩展形式[13]：

为了简化问题，我们下面以标准Krylov子空间k为代表对算法进行设计。设第k次扩充时Krylov子空间为

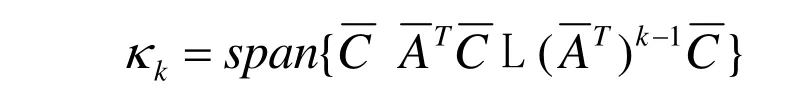
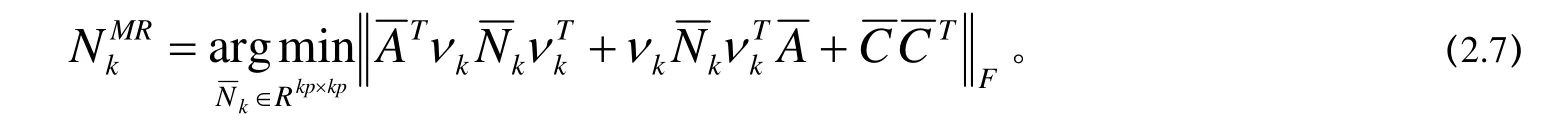
不失一般性，引入算子

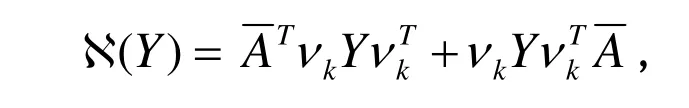
则（2.7）等价为

下面我们讨论（2.8）的求解。为加快收敛速度，我们尝试采用一些理论成熟的预条件方法，如采用预条件共轭梯度最小二乘方法（PCGLS）求（2.8）的解。利用拉直算子可将（2.8）化为矩阵-向量方程形式，为方便起见，我们直接使用其矩阵-矩阵形式。记算子À的伴随算子为取预条件子为M，从而，求解 （2.8）的PCGLS算法可描述如下：

算法 2.2 （PCGLS）

结合算法2.1和2.2，我们得到了如下求解ARE（1.1）的基于最小残差的预条件共轭最小二乘牛顿迭代算法。算法 2.3 （ARE-MINRES-PCGLS-NM）

Step 4.利用Arnold算法或分块Arnold算法[11]扩充Krylov子空间kk，得到kn和nk+1；

从算法2.3可以看出，内循环变量k的每次增加都要求用PCGLS方法求解一个最小残差F-范数的优化问题。但事实上，在迭代过程中，我们真正关心的只是残差的F-范数值用以判定算法是否继续迭代，并不关心此时方程（2.8）的解，只有在达到收敛条件时才需要计算其解。基于此，我们可以对算法2.3进行改进，采用新的策略直接对（2.8）中的范数进行估计，而略去计算中间步骤中的求解过程，只在范数达到条件时才计算。显然，这能够大大节省计算成本，加快收敛速度，尤其是在矩阵方程的阶数较大的情形。为此，先介绍下面两个引理。

3　数值实验

下面我们将运用算法2.4求解ARE（1.1）的实例。实验是在硬件环境CPU为 Pentium（R） Core Dual E5400，内存为 2G ，软件环境为 Matlab R2009a 下完成。为简单起见， 取ARE（1.1）中 E为单位矩阵。由于空间Ek所含信息涵盖了空间k，

因此，在实验中用kE代替算法2.4中k。

3.1收敛准则

在算法2.4中我们将采用如下关于相对残差范数取值作为外迭代收敛准则

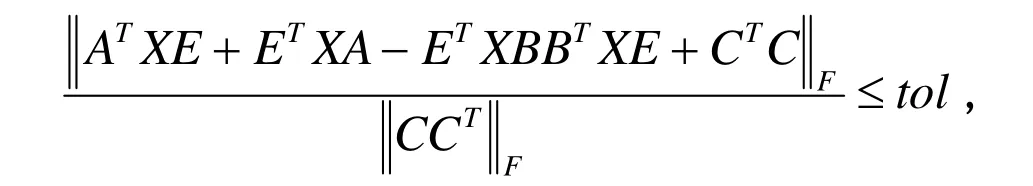
利用（2.11）计算得到的残差范数minRes来判断内迭代是否完成，即是否要计算相应Lyapunov方程的解。为使求解ARE获得较高精度，这要求相应的Lyapunov方程求解具有一个较高的精度。因此，我们直接取 minRes

3.2预条件子的取法

由于预条件子M的主要作用是使M能尽量与À*À接近，又

因此，可取算子M满足

3.3实验结果

我们以一个钢轨冷却系统模型[13]为研究对象，其冷却过程可以用一个不稳定的二维热方程进行描述，对其进行有限元半离散后最终该模型转化为对形如（1.1）的代数Riccati方程求解。在稍作处理后，取定s=t=6，表3.1给出了阶 n=821

表3.1 数值实验结果

从表3.1可以看出，算法2.4对ARE（1.1）的求解是非常有效的。

[1]Laub A.A schur method for solving algebraic Riccati equations[J].IEEE Trans. Automat. Control.,1979,24:913-921.

[2]Byers R.Solving the algebraic Riccati equation with the matrix sign function[J].Linear Algebra Appl.,1987,85:267-279.

[3]H.T.Banks,K.Ito.A numerical algorithm for optimal feedback gains in high dimensional linear quadratic regulator problems[J]. SIAM J.Control.Optim.,1991,29(3):499-515.

[4]J.A.Burns,K.P.Hulsing.Numerical methods for approximating functional gains in LQR boundary control problems[J]. Mathematical and Computer Modelling,2001,33(1):89-100.

[5]D.Kleinman.On an Iterative Technique for Riccati Equation Computations[J].IEEE Transactions on Automat.Control.,1968,13: 114-115.

[6]I.G.Rosen and C. Wang.A multilevel technique for the approximate solution of operator Lyapunov and algebraic Riccati equations [J].SIAM J.Numer.Anal.,1995,32(2):514-541.[7] P. Benner and J. Saak. A Galerkin-Newton-ADI method for solving large-scale algebraic Riccati equations [J]. DFG Priority Programme 1253 "Optimization with Partial Differential Equations", 2010. Preprint SPP1253-090.

[8] Gajic Z, Qureshi M. Lyapunov Matrix equation in system stability and control [M]. Academic Press: San Diego, 1995.

[9] P. Benner, J. R. Li, T. Penzl. Numerical solution of large-scale Lyapunov equations, Riccati equations, and linear-quadratic optimal control problems [J]. Numer. Linear Algebra Appl., 2008, 15(9):755–777.

[10] Lin Y, V. Simoncini. Minimal residual methods for large scale Lyapunov equations [J]. Appl. Numer. Math., 2013, 72:52-71.

[11] Y. Saad. Iterative methods for sparse linear systems [M]. 2nded., Society for Industrial and Applied Mathematics, Philadelphia, PA, 2003.

[12] Kemin Zhou, John C.Doyle, Keith Glover. Robust and optimal control [M]. New Jersey: Prentice Hall, 2007.

[13] V.Simoncini. A new iterative method for solving large-scale Lyapunov matrix equations [J]. SIAM J. Sci. Comput., 2007, 29(3): 1268–1288.

（责任编校：何俊华）

O241.6； O151.21

A

1673-2219（2015）05-0005-06

2014－12－05

湖南省教育厅资助科研项目（12C0688），湖南省自然科学基金资助项目（12JJ3077）。

周立平（1978－），男，湖南永州人，副教授，硕士，研究方向为数值代数和偏微分方程数值解。