关于椭圆曲线y2=px（x2+2）的正整数解的一个注记

刘先蓓

（安徽财经大学统计与应用数学学院，安徽蚌埠233030）

关于椭圆曲线y2=px（x2+2）的正整数解的一个注记

刘先蓓

（安徽财经大学统计与应用数学学院，安徽蚌埠233030）

取p 是满足p≡1（mod 8）的奇质数，运用同余与整除的性质，给出了椭圆曲线y2=px（x2+2）的正整数解的一个性质，并证明了当p=8 537时该椭圆曲线只有一组正整数解（x，y）=（392，717 108）。

椭圆曲线；同余；正整数解

J.W.S.CASSELE［1］利用四次代数数域的性质证明了p=3时椭圆曲线

仅有（1，3）、（2，6）和（24，204）三组正整数解。F.LUCA和P.G.WALSH运用四次Diophantine方程的性质给出了上述结果的一个新的证明方法，并证明了p为奇质数时椭圆曲线（1）至多有3组正整数解［2］。陈历敏证明了椭圆曲线（1）在p≡5或p≡7（mod 8）时没有正整数解，在p≡1（mod 8）时至多有一组正整数解，在p≡3（mod8），且p＞3时至多有两组正整数解［3］。管训贵证明了椭圆曲线（1）在p=2 573时只有一组正整数解（x，y）=（73，31 116）［4］。最近，张瑾给出了椭圆曲线（1）在p≡1（mod8）时有正整数解的判别条件［5］。在此基础上，笔者利用同余与整除的性质得出了p是满足p≡1（mod 8）的奇质数时椭圆曲线y2=px（x2+2）的正整数解的一个性质，并证明了当p=8537时，该椭圆曲线只有一组正整数解（x，y）=（392，717108）。

1 相关引理

引理1［3］：当p＞3时，方程X2-2p2Y4=1无正整数解。

引理2［6］：若D1＞1，D1和D2互质，且D1、D2为非平方的正整数，则方程D1X2-D2Y4=1至多有1组正整数解。

给定的正整数n ，可唯一地表示为n=fm2，其中f、m均为正整数，且f无平方因子，记为f=f（n）。

引理3［5］：假设p≡1（mod 8），则椭圆曲线（1）有正整数解的充要条件是p满足

且当条件（2）成立时，椭圆曲线（1）有唯一正整数解

其中a 是满足32b4+1=pa2的正整数。

2 主要结论

利用同余式和整除性理论，可以得到以下定理。

定理1：设（x，y）为椭圆曲线（1）的正整数解，若质数p≡1（mod 8），则x必为偶数。

证明：利用反证法，若x 不是偶数，则x必为奇数，这时有gcd（x，x2+2）=1。取x=s2，x2+2=pt2时，由（1）式可得y=pst；取x=ps2，x2+2=t2时，由（1）式可得y=pst。在以上式子中，s和t为互质的奇数。

因为s2≡t2≡1（mod 8），且p≡1（mod 8），所以x≡1（mod 8），且x2≡7（mod 8）。由x≡1（mod 8）知x2≡1（mod 8），这与x2≡7（mod 8）矛盾，故x必为偶数。

定理2：当p=8 537时，椭圆曲线（1）只有一组正整数点（x，y）=（392，717 108）。

证明：当8 537≡1（mod 8）时，由定理1可知，x为偶数，则有gcd（x，x2+2）=2。取

或

其中s、 t为互质的正整数。若（4）式成立，则有

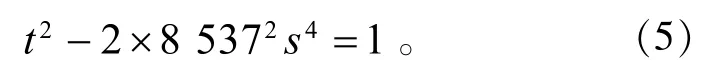
由引理1知，（5）式无正整数解。

若（3）式成立，则有

由引理2可知，（6）式至多有一组正整数解（s，t），因而椭圆曲线（1）至多只有一组正整数解（x，y）。由于x为偶数，故t为奇数。

取t=3时，可得s=14，代入（3）式，可得椭圆曲线（1）的正整数解（x，y）=（392，717 108）。

下面给出定理2的另一个证明。

由于8 537≡1（mod 8），且8 537×32=32×74+1，则由引理3可知，椭圆曲线（1）有正整数解，正整数解为（8×72，4×8 537×3×7）=（392，717 108）。

说明：若通过计算机程序搜索10 000以内p≡1（mod 8）的质数对应的椭圆曲线（1）所有x＜106的正整数解（x，y），则可以得出如下结论。

仅当p取2 953或8 537时，椭圆曲线（1）才有x＜106的正整数解。

在此基础上，提出猜想：若p≡1（mod 8），且p＜10 000，则当且仅当p取2 953或8 537时椭圆曲线（1）才有正整数解。

［1］CASSELS J W S.A Diophantine Equation［J］.Glasgow Math J，1985，27（1）：11-18.

［2］LUCA F，WALSH P G.On a Diophantine Equation of Cassels［J］.Glasgow Math J，2005，47（2）：303-307.

［3］陈历敏.Diophantiney2=px（x2+2）方程［J］.数学学报，2010（1）：83-86.

［4］管训贵.关于Diophantine方程y2=px（x2+2）［J］.北京教育学院学报（自然科学版），2011（1）：1-2.

［5］张瑾.椭圆曲线y2=px（x2+2）有正整数点的判别条件［J］.数学的实践与认识，2005（4）：232-235.

［6］LJUNGGRENW.EinSatzUberDieDiophantische GleichungAx2-By4=C（C =1，2，4）［J］.Tolfte Skand Mat Lund，1953，12：188-194.

【责任编辑 王云鹏】

A Note on the Positive Integer Solutions of the Elliptic Curve y2=px（x2+2）

LIU Xianbei
（Institute of Statistics and Applied Mathematics，Anhui University of Finance and Economics，Bengbu 233030，China）

Supposingp was an odd prime withp≡1（mod 8）.In this paper，using the properties of congruence and divisibility，we gave a property for the positive integer solutions（x，y）of the elliptic curvey2=px（x2+2）.In addition，it was proved that the only positive integer solution of the elliptic curve was（x，y）=（392，717 108），whenp=8 537.

the elliptic curve；congruence；positive integral solution

O156

A

2095-7726（2015）12-0012-02

2015-07-24

安徽财经大学学校课题资助项目（ACKY1550）

刘先蓓（1982-），女，安徽广德人，讲师，硕士，研究方向：数论及其应用。