具有Beddington-DeAngelis功能反应的捕食系统的全局分析
梁桂珍,丰莹莹
(1.新乡学院数学与信息科学学院,河南新乡453003;
2.郑州大学数学与统计学院,郑州450001)
具有Beddington-DeAngelis功能反应的捕食系统的全局分析
梁桂珍1,丰莹莹2
(1.新乡学院数学与信息科学学院,河南新乡453003;
2.郑州大学数学与统计学院,郑州450001)
研究了具有Beddington-DeAngelis功能反应的捕食系统,该系统包含具有阶段结构和时滞特征的捕食者种群和两类具有互惠关系的食饵种群。通过比较原理得到了该系统持续生存和捕食者灭绝的充分条件,并证明了该系统为周期系统时其正周期解的存在性和全局稳定性。
阶段结构;时滞;互惠关系;持续生存;Beddington-DeAngelis功能反应
捕食系统方面的研究是现代生态学领域的重要课题。研究结果表明,在低密度状态下,具有Beddington-DeAngelis功能反应的捕食系统与实际情况更加吻合。近年来,国内外学者对具有该功能反应的捕食系统进行了多方面的研究,这些研究包括捕食系统的持久性、时滞和周期解的稳定性[1-4],但具有互惠关系的食饵种群方面的研究尚不多见。陈婷和魏凤英研究了具有阶段结构特征的捕食者和两类具有竞争关系的食饵组成的生态系统的持久性[4]。在此基础之上,我们分析、研究了具有Beddington-DeAngelis功能反应的捕食系统,通过比较原理得到了该系统持续生存和捕食者灭绝的充分条件,并证明了该系统为周期系统时其正周期解的存在性和全局稳定性。
1 系统描述
在本文中,我们考虑了一类具有阶段结构和时滞特征的捕食者种群、两类具有互惠关系的食饵种群以及捕食者对食饵的Beddington-DeAngelis功能反应,并建立了捕食系统

在系统(1)中,x1(t)和x2(t)分别表示两类食饵种群的密度,y1(t)和y2(t)分别表示捕食者幼年期和成熟期的种群密度,e1(t)和e2(t)分别表示两类食饵种群间的竞争率,r1(t)和r2(t)分别表示食饵种群的内禀增长率,b1(t)、b2(t)和b3(t)分别代表种群的密度制约,d1(θ)和d2(t)分别表示捕食者幼年期和成熟期的种群死亡率。


2 相关的定义和引理



由(3)式可以证明,当t≥-τ时,有y1(t)>0。
综合以上证明过程可知,系统(1)满足条件(2)的任一解都是正的,即是系统(1)的正向不变集。
3 系统的持续生存性


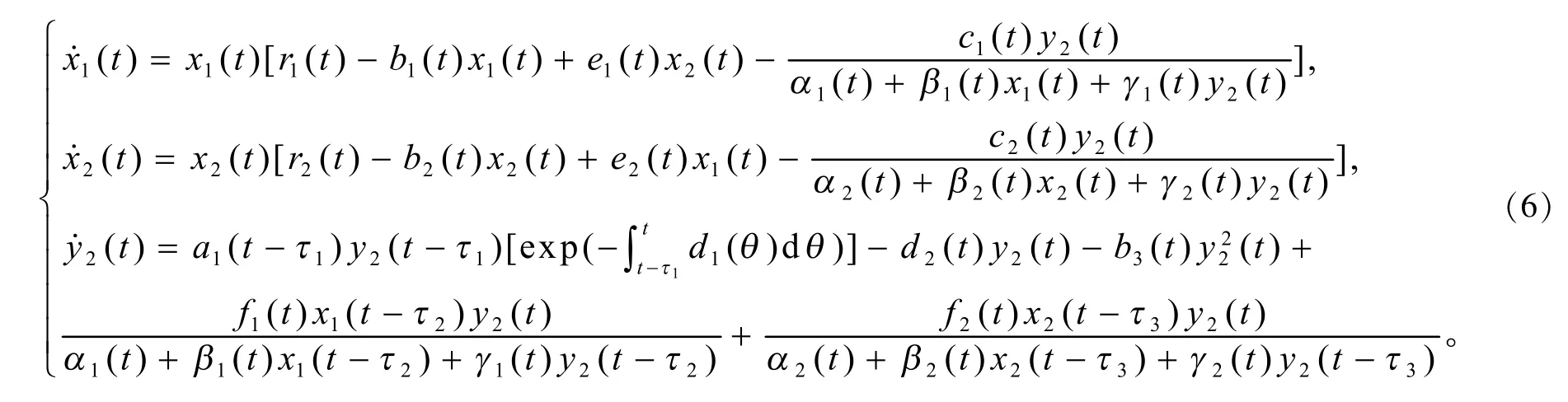
由系统(6)的前两个方程,并结合x1(0)、x2(0)的取值,可以得出如下3个结论:


由(6)式的前两个方程,并结合x1(0)、x2(0)的取值,可以得出如下3个结论:


综上所述,并由定义1可知,系统(1)是持续生存的。
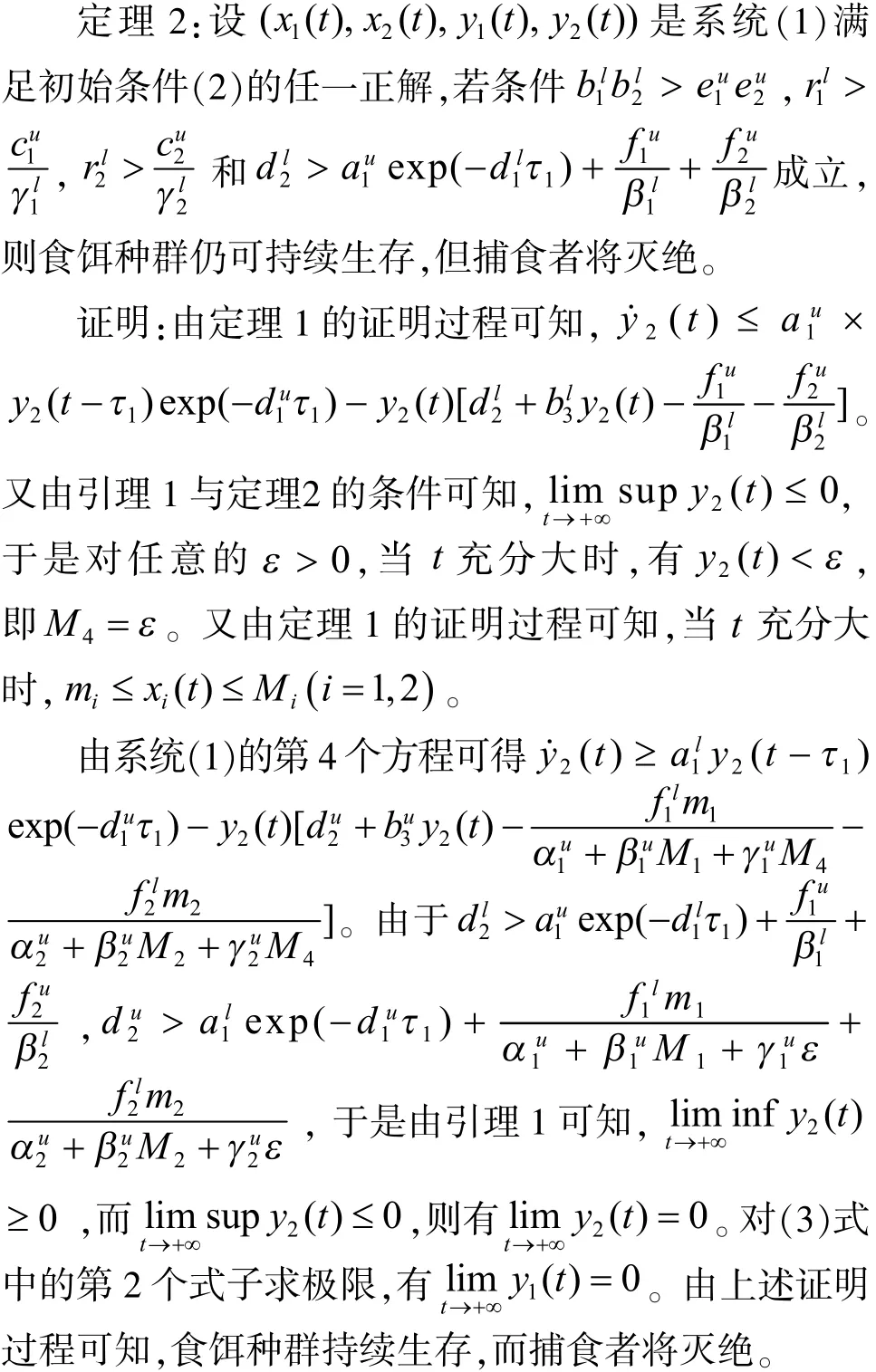
4 正周期解的全局稳定性
在以下证明过程中,我们假设系统(1)的所有系数都是以ω为周期的正连续有界函数,这时系统(1)也称为ω周期系统。


定理4:假设
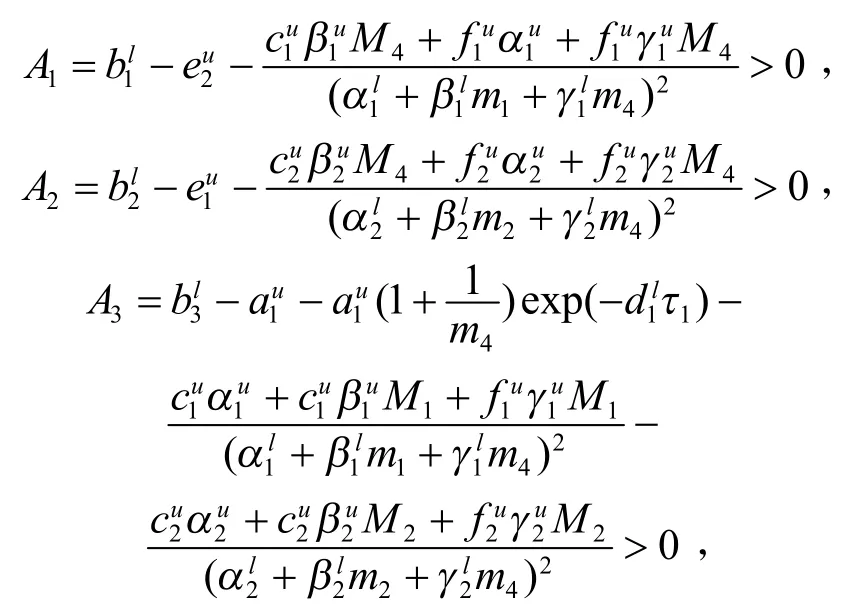
若满足初始函数(2)的系统(1)满足定理1的条件,则系统(1)是全局稳定的。



5 举例
为了说明周期解的全局稳定性,我们给出生态系统

可以验证,系统(7)的系数满足定理4的条件。取初始条件为x1(0)=6,x2(0)=10,y1(0)=1,y2(0)=2,并运用Matlab软件进行数值模拟,计算结果见图1。由图1可以看出,系统(7)的解是全局稳定的。
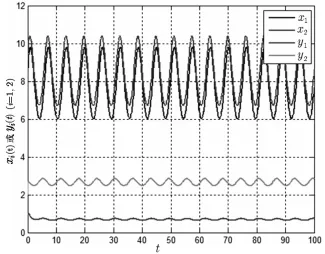
图1 系统(7)的周期解的全局稳定性
6 结束语
通过研究一类具有Beddington-DeAnglis功能反应的捕食系统,我们得到了捕食系统持续生存和捕食者灭绝的充分条件,即只有当捕食者成年和幼年的种群密度达到一定程度时,它才不会灭绝。另外,我们还通过Brouwer不动点定理,证明了该系统是周期系统时其正周期解的存在性,并通过构造Liapunov函数,证明了周期解的全局稳定性。
[1]ZHENG X L,MENG X L,GAO Y P,et al.Study on A Non-autonomous Predator-prey Dispersion-delay Model with Beddington-DeAngelis Functional Response[J]. Journal of Biomathematics,2014(2):231-247.
[2]吴丽萍.一个具有Beddington-DeAngelis功能反应的离散捕食者-食饵系统的持久性[J].北华大学学报(自然科学版),2013(6):626-630.
[3]熊友兵.具有Beddington-DeAngelis功能反应的时滞捕食者-食饵模型的周期解[J].天津工业大学学报,2007(3):81-85.
[4]陈婷,魏凤英.具有年龄结构一捕食两竞争食饵生态系统的持久性[J].福建师大福清分校学报,2009(5):1-5.
[5]梁桂珍,李坤.非自治的具有阶段结构和时滞的捕食系统的动力学行为[J].数学杂志,2011(3):415-422.
[6]田宝丹,王海玲.具有HollingⅠV类功能性反应的非自治扩散系统的持久生存[J].四川师范大学学报(自然科学版),2004(6):610-613.
【责任编辑 王云鹏】
Global Analysis of a Predator-prey System with Beddington-DeAngelis Functional Response
LIANG Guizhen1,FENG Yingying2
(1.School of Mathematics andInformation Science,Xinxiang University,Xinxiang 453003,China;
2.School of Mathematics and Statistics,Zhengzhou University,Zhenzhou 450001,China)
In this paper,a predator-prey system with Beddington-DeAngelis functional response was investigated.The system comprised the stage structure feature,the predator population with delay feature and two prey populations with mutually beneficial relationship.According to the comparative principle,some sufficient conditions were proved for the permanence of the system and extinction of the predator,and some sufficient conditions were proved for the existence and global stability of positive periodic solution when this system was a periodic system.
stage structure;delay;mutually beneficial relationship;permanence;Beddington-DeAngelis functional response
O175.21
A
2095-7726(2015)06-0001-06
2015-07-02
河南省科技厅科技攻关项目(122102310373,132102310482);新乡学院科技创新项目(12ZB17)
梁桂珍(1964-),女,内蒙古临河人,教授,硕士,研究方向:生物数学和非线性分析。

