基于神经网络响应面的鱼雷总体性能参数仿真优化方法
范若楠,曾 进,任庆生,李 斌
(1. 中国船舶重工集团公司 第705研究所,陕西 西安,710075; 2. 上海交通大学数学系,上海,200240; 3. 上海交通大学 计算机科学与工程系,上海,200240)
基于神经网络响应面的鱼雷总体性能参数仿真优化方法
范若楠1,曾进2,任庆生3,李斌1
(1. 中国船舶重工集团公司 第705研究所,陕西 西安,710075; 2. 上海交通大学数学系,上海,200240; 3. 上海交通大学 计算机科学与工程系,上海,200240)
利用水声寻的仿真进行鱼雷总体性能参数优化匹配时,需要获取大量的仿真样本数据,为节省优化时间,节约优化成本,提出了一种基于神经网络响应面(NN-RSM)的鱼雷总体性能参数仿真优化方法。利用神经网络构建能够快速计算的响应面,并通过空间映射方法获得水声仿真系统的最优解,最后利用该方法对自导作用距离、毁伤半径等鱼雷总体性能指标进行了仿真优化。优化结果显示,该方法不仅能够获得原问题有效的优化结果,且优化计算时间小于普通优化方法的1/20。该方法可以进一步拓展应用到其他复杂系统多参数、多目标的仿真优化中。
鱼雷; 总体性能优化; 神经网络; 响应面; 空间映射
0 引言
鱼雷是极具特色的水下精确制导武器,如何根据作战需求优化设计鱼雷总体性能指标,提高鱼雷实际作战环境中的效能,始终是鱼雷型号研制和总体技术研究的重点。这方面的相关研究很多,黄科人等用遗传算法探讨了大深度鱼雷发射管的优化设计方法[1]; 段富海等人通过对控制器参数离线寻优等方式设计了非线性鱼雷系统弹道深度控制器[2]; 郭勍等人基于广义功极小值原理初步研究了鱼雷的姿态最优控制和最优制导问题[3]; 聂卫东等人基于庞特里亚金(Pontryagin)极小值原理研究了轻型反潜鱼雷的最优垂直命中导引律[4]。但利用水声寻的仿真进行鱼雷总体性能的优化研究始终是鱼雷研究中的难点,也是迫切需要解决的研究热点。
目前鱼雷总体设计的研究领域包括雷体线型、鳍舵、推进器、壳体结构、总体布置、弹道、声学和可靠性等领域,这就使得用于研究其作战效能的水声寻的仿真系统构成非常复杂,其基本组成原理框图如图1所示,也使得在此基础上的性能参数优化研究极具挑战性。
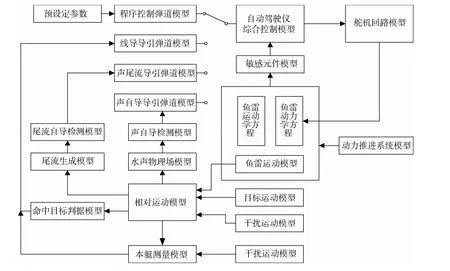
图1 鱼雷全弹道数学仿真模型Fig. 1 Mathematical simulation model of torpedo▯s complete trajectory
文章从节约计算成本出发,首先建立一个能够快速计算的基于神经网络响应面的粗糙仿真模型。由于近似的神经网络响应面与原仿真模型存在差异,使得这2个模型的最优值与最优值点不尽相同,从而导致在神经网络响应面基础上求得的最优值与最优值点往往不是原模型的最优解,但与以往研究最大的不同是,寻优算法并不直接在神经网络响应面上求最优解,而是借助于神经网络响应面快速响应的特点,利用空间映射方法引导寻优过程,以较少的计算成本获得原仿真模型的有效优化结果,优化计算时间可以从8 h左右减少到不足20 min。
1 数学模型
文章以鱼雷长度、沾湿表面积、自导作用距离、毁伤半径、自导扇面宽度、末程拦截距离和比例导引法系数作为优化参数,以最小脱靶量和最短航程为优化目标,这是一个典型的多参数、多目标的优化问题,其数学描述形式为
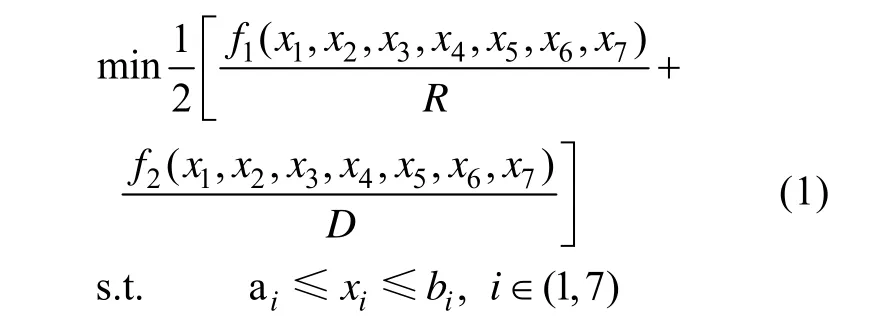
式中: x1为鱼雷长度; x2沾湿表面积; x3为自导作用距离; x4为毁伤半径; x5为自导扇面宽度;x6为末程拦截距离; x7为比例导引法系数; R为引信作用距离; D为航程最大值。而f1( x1,x2,x3,x4,x5,x6,x7)为鱼雷与目标的最近距离,f2(x1,x2,x3,x4,x5,x6,x7)为鱼雷航程,它们均由一个鱼雷寻的—导引—命中全过程的、集成的仿真系统给出(见图1)。
在给定鱼雷长度等参数条件下,由于仿真计算过程涉及鱼雷运行的全过程,因此由仿真程序计算目标函数f1与f2的计算时间过于漫长,在目前常规的微机(CPU: 3 GHz; 内存: 4 GB)上进行一次计算需要近3.5 min,这使得在此基础上的寻优研究会面临计算时间代价过大的问题(因为最优解的质量往往直接决定于解空间的搜索量,即仿真程序的计算次数)。因此快速优化算法的研究变得非常重要。
文章先利用神经网络响应面建立一个快速的近似仿真模型,该模型虽然计算效果比已有仿真程序差,但计算速度快。然后在此基础上利用空间映射方法,将大部分原先基于精确仿真模型的优化工作转移到神经网络响应面,同时利用精确仿真模型进行修正,从而能够在较短的时间内给出鱼雷总体性能参数最优化结果。
2 神经网络响应面
2.1BP算法
D.E.Rumelhart和J.L.McClelland提出了一种利用误差反向传播训练算法的神经网络,简称BP(back propagation)神经网络[5]。它是一种有隐含层的前馈系统。若网络的输入节点为M,输出节点数为L,则该网络可以看作一个从M维欧氏空间到L维欧氏空间的非线性映射,因此这种网络模型在非线性函数逼近中获得广泛应用。
BP算法的中心思想是通过调整权值来使得网络的总误差最小,其学习过程是一种误差向后传播并修正权系数的过程。在运用BP学习算法的时候,实际上有正向和反向传播2个阶段,正向传播过程中,输入信息从输入层经过隐含层逐层处理,最后传向输出层; 其中,每一层神经元的状态只影响下一层神经元的状态。如果输出层的输出结果与期望值有偏差,则进入反向传播,依据误差来修改各层的权值,使误差信号最小。
图2为具有一个隐含层的BP网络,其中输入节点有M个,分别为x1,x2,…,xM,输出节点有L个,网络的隐含层共有Q个神经元。
当隐层使用S型函数,输入和输出层使用线性函数时,神经网络可对任意连续函数进行逼近,而增加隐层可以在一定程度上减小网络规模,提高推广能力。图2中的Wih和Whj是待定参数,称为权值,可通过样本学习获得。
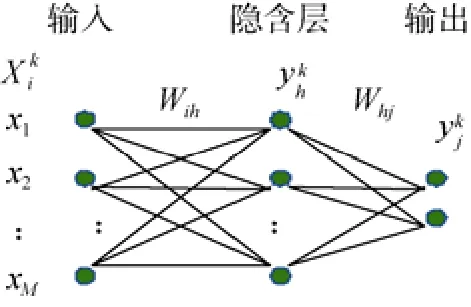
图2 具有隐含层的BP网络Fig. 2 BP networks with hidden layer
2.2学习样本点的获取
响应面方法以试验设计为基础,试验设计对模型精度有很大影响,需要能够反映设计空间特性的样本点,样本点选取的好坏对后面近似模型的精确度和问题的优化起着非常重要的作用。
采用拉丁超立方方法[6]进行样本点的选取。拉丁超立方体抽样(latin hypercube sampling,LHS)是一种对抽样分布全面分层,再从每层中随机取值的方法。它使得输入组合相对均匀地填满整个试验区间,每个因素的设计空间都被均匀划分,并且所有因素都有同样数目的分区,每一个因素的每个水平只被研究一次。
LHS能够以较少的样本点反映整个设计空间的特性,成为一种有效的样本缩减技术,具有效率高,均衡性能好的优点。
LHS方法需假设在n维向量空间里抽取m个样本,具体步骤如下。
1)将每一维分成互不重叠的m个区间,使得每个区间有相同的概率(通常考虑一个均匀分布,这样区间的长度相同);
2)在每一维里的每一个区间中随机的抽取一个点;
3)再从每一维里随机抽出步骤2)中选取的点,将它们组成样本向量。
2.3神经网络的学习效果
由于本问题的复杂性,通过LHS方法分别构造了规模为3 000的学习样本集和规模为200的测试样本集。在仿真研究中采用的网络结构为7个输入单元和1个输出单元,对不同的隐层结构做了仿真,结果如表1所示。
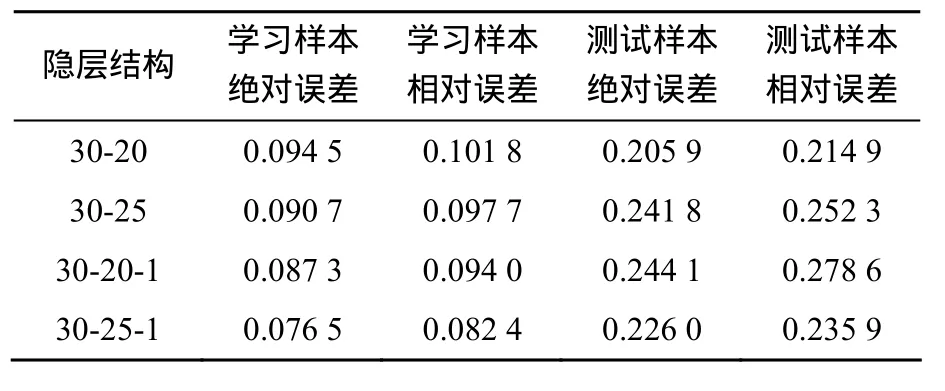
表1 神经网络仿真结果Table 1 Simulation results of neural network
从表中可以看到,学习误差可以随着网络结构复杂性的增加而降低,但相应的测试误差却会增加,说明网络结构的复杂性增加时,对学习样本的特征学习加强了,但却产生了过学习的情况,网络学习了过多的样本细节,却未能充分反映样本内含的规律,导致不能很好处理未学习过的新样本。这也同时说明,鱼雷的仿真过程是一个极度复杂的强非线性系统,针对这个复杂系统,已经为其设计了一个5层网络,但并没有得到非常好的拟合效果。与原有的仿真系统计算结果相比,神经网络响应面的计算结果还存在比较大的误差。
为此,引入空间映射的概念,建立原仿真系统与神经网络响应面的对应关系,不是直接在神经网络响应面上求解最优值,而是利用神经网络响应面的快速运算能力和快速寻优能力去逼近原仿真系统的最优值。
3 基于空间映射的优化过程
考虑如下优化问题

对R分别建立精确模型Rf(xf)和粗糙模型Rc(xc)。精确模型Rf对于原系统R能够准确拟合,但计算速度慢,其最优解即使能够求解,计算成本也会非常高昂。粗糙模型Rc虽然只能大致反映原始系统R的特性,但计算速度快,能较快获得其最优解,但若直接将代入Rf则其值并不理想。为此,空间映射理论[7]假设精确模型和粗糙模型的变量空间之间存在映射P,满足


图3 空间映射Fig. 3 Space mapping
空间映射的优势在于把许多优化工作放在粗糙空间中完成,而在精确空间中只进行优化结果的验证,这样能够充分利用粗糙模型的快速高效性和精确模型的准确性,以较少的计算成本获得有效的优化结果。
在最早提出的初始空间映射方法[7]中,会在附近随机选择一定数量的样本点作为精确空间的初始设计点,然后逐个求出这些点在精确空间中的响应值,再通过参数提取获得相应的粗糙空间设计基点,最后根据2个空间的样本基点建立两者的线性映射关系。
初始空间映射方法由于一开始要进行一定量基点的精确计算,计算时间仍然比较长,且线性关系通常不足以反映2个空间之间的关联,因此提出了主动空间映射方法,该方法结合拟牛顿迭代法求解方程主动空间映射方法由粗糙模型最优解获得精确模型最优解的估计值,每次精确模型计算结果都参与映射关系P的建立,通过Broyden 1阶导数近似关系式对精确模型设计参数进行预测和更新。该算法易实现,计算效率高,其计算流程如下。
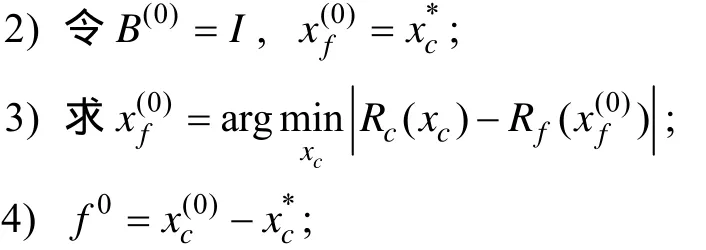
5)j=0,并重复以下步骤直至满足一定的终止标准:


4 仿真结果与分析
目前已有的仿真系统能够较好地模拟鱼雷的寻的和攻击目标过程,直接将其作为精确模型。该精确模型在给定7个参数时能够较准确地给出相应的性能指标f,但计算时间约为3 min。如果直接在这一精确模型的基础上进行优化,由于需要多次计算f的值,总的计算时间需要8 h以上。
与此同时,为该系统建立了一个基于神经网络响应面的粗糙模型,其输入输出与精确模型相同,能够大致反映原始鱼雷系统的性能,计算速度快,利用这一粗糙模型进行常规的优化计算仅用20 s左右就能够得到结果,但该结果如果直接代入精确模型,则所得到的实际输出很差,即粗糙模型的最优参数不能直接用于精确模型,需要进行修正。
为此,文中使用了主动空间映射方法进行优化计算,图4和图5展现的是寻优过程中所获最优值随精确模型计算次数的变化情况,横坐标表示精确模型的计算次数,纵坐标表示所获得的最优解。图4体现了传统优化算法的优化过程,通过近150次精确模型的计算,耗时近8 h,得到精确模型的最优值为0.346 1,即优化目标的最小值。图5体现的是使用主动空间映射方法的优化过程,在这个过程中,精确模型和粗糙模型都参与了计算,虽然粗糙模型的计算次数有400多次,但由于整个寻优过程仅用到了5次精确模型的计算,整个计算过程耗时不到20 min,获得的精确模型的最优值为0.346 2。该结果与精确模型的最优解结果一致,符合该问题在工程实际经验中的参数取值和优化结果。表2为直接优化方法与空间映射优化方法得到的最优值所对应的优化参数对比。由表中可以看出,2种算法得到的7个优化参数差值比较小,参数差在参数搜索空间中的比例均不高于6%,说明当空间映射方法的优化结果收敛到最优值时,其参数取值也收敛到一个较小的参数取值空间。

图5 空间映射优化方法计算结果曲线Fig. 5 Curve of computation result with space mapping optimization method

表2 2种方法的参数优化结果对比Table 2 Comparison of parameter optimization between two methods
5 结束语
鱼雷全弹道仿真系统由于全面考虑鱼雷运行过程中涉及的诸多因素,使仿真过程耗时较长,为在此基础上的优化增加了难度。为了更快捷有效地获得此问题的最优设计方案,提出用神经网络法先建立一个近似仿真系统,并通过空间映射法建立此近似仿真系统与原仿真系统的联系,借助于神经网络近似仿真系统的快速运算能力和快速搜索能力,快速搜索到原鱼雷全弹道仿真系统的最优解,具体的优化计算结果显示该方法是可行和有效的,可以进一步拓展到其他复杂系统多参数、多目标的仿真优化之中。
[1] 黄科,高兴,段浩,等. 基于遗传算法的鱼雷发射管优化设计[J]. 鱼雷技术,2013,21(2): 156-160.
Huang Ke,Gao Xing,Duan Hao,et al. Optimization Design of Torpedo Launch Tube Based on Genetic Algorithm[J]. Torpedo Technology,2013,21(2): 156-160.
[2] 段富海,章卫国,何长安. 一种非线性优化控制方法及其在鱼雷控制中的应用[J]. 控制理论与应用,2000,17(1): 65-68.
Duan Fu-han,Zhang Wei-guo,He Chang-an. A Nonlinear Optimal Control Method and Its Application in the Torpedo Control[J]. Control Theory and Application,2000,17(1): 65-68.
[3] 勍郭,党涛立,范奎武. 基于广义功极小值原理的鱼雷最优控制问题[J]. 鱼雷技术,2006,14(5): 38-41. Guo Qing,Dang Tao-li,Fan Kui-wu. Optimization Control of Torpedo Based on Generalized Work Minimum Principle[J]. Torpedo Technology,2006,14(5): 38-41.
[4] 聂卫东,高智勇,刘艳波. 轻型反潜鱼雷最优垂直命中末弹道设计[J]. 鱼雷技术,2012,20(1): 1-7.
Nie Wei-dong,Gao Zhi-yong,Liu Yan-bo. Optimization Design of Perpendicular Hit Terminal Trajectory for Lightweight Antisubmarine Torpedo[J]. Torpedo Technology,2012,20(1): 1-7.
[5] Rumelhart D E,McClelland J L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition [M]. Cambridge: MIT Press,1986.
[6] 方开泰,王元. 数论方法在统计中的应用[M]. 北京:科学出版社,1996: 222-224.
[7] Bandler J W,Biernacki R M,Chen S H,et al. Space Mapping Technique for Electromagnetic Optimization[J]. IEEE Transactions on Microwave Theory and Techniques,1994,42(12): 2536-2544.
(责任编辑: 陈曦)
Optimization Method of Overall Performance Parameters of Torpedo via Simulation Based on Neural Network Response Surface
FAN Ruo-nan1,ZENG Jing2,REN Qing-sheng3,LI Bin1
(1.The 705 Research Institute,China Shipbuilding Industry Corporation,Xi▯an 710075,China; 2. Department of Mathematics,Shanghai Jiaotong University,Shanghai 200240,China; 3. Department of Computer Science and Engineering,Shanghai Jiaotong University,Shanghai 200240,China)
Underwater acoustic homing simulation can exhibit operational effectiveness of a torpedo in a real environment,however a large number of sample data is needed in the simulation for the overall performance parameters optimization of the torpedo,thus optimization time becomes the bottleneck. Based on the quick neural network response surface method(NN-RSM),this paper uses the space mapping method to reduce the cost of optimization calculation and directly get the optimal solution to the underwater acoustic homing system. Subsequently,the overall performance indices of a torpedo,such as homing range and damage radius,are optimized. Optimization results show that effective optimization of the original problem is achieved with computation time less than 1/20 that of the general optimization methods. The present method can be applied to optimization of other complicated system with multiple parameters and multiple objectives.
torpedo; overall performance optimization; neural network; response surface; space mapping
TJ630.1
A
1673-1948(2015)05-0326-06
10.11993/j.issn.1673-1948.2015.05.002
2015-05-20;
2015-06-09.
范若楠(1984-),女,硕士,主要研究领域为鱼雷仿真技术.

