同步器静态挂挡力与行程曲线分析
章刚,邱辉鹏
(陕西法士特公司研究院设计所,陕西西安710119)
同步器静态挂挡力与行程曲线分析
章刚,邱辉鹏
(陕西法士特公司研究院设计所,陕西西安710119)
通过分析锁环式同步器换挡过程中与滑动齿套行程相关的结构或尺寸,分段研究换挡各位置的挂挡力及计算公式,得到典型锁环式同步器单体静态挂挡力和挂挡行程的理论曲线;通过与试验结果比较,发现理论计算结果准确可信,该典型锁环式同步器挂挡力峰值位置与动态同步锁止位置吻合。
锁环式同步器;静态挂挡力;行程曲线
0 引言
随着汽车保有量的持续增加,路面交通状况也日见恶化,频繁的换挡操作使得用户对换挡品质的要求越来越高。影响变速换挡性能的因素很多,如换挡杆、软轴、换挡轴、换挡拨叉及同步器等。其中同步器作为实现车辆换挡操作迅速轻便无冲击、提高动力性和燃料经济性的关键零部件,对换挡品质有重要影响[1]。
汽车静态换挡性能对动态换挡,特别是高挡区换挡性能和空挡稳定有重要作用,而且作为变速器乃至汽车性能最初步最直观的评价之一,现在越来越受到主机厂和变速器厂商的重视。目前的换挡品质评价(包括静态换挡性能评价)主要通过主观打分或测量挂挡力峰值来评价,这两种方法要么主观性强,要么不能完全反应换挡品质即手感的好坏;更准确的评价方式是通过试验得到换挡性能曲线来评价[2-3]。但对于新产品,不可能一次就得到理想的换挡性能曲线,往往需要反复试制、试验、再试制……,这种循环改动设计周期长,成本巨大;因此,在设计初期即掌握新产品的换挡性能曲线,至少是静态换挡曲线对提升变速器产品的换挡品质具有重要意义。
作为重型机械式变速器换挡性能分析改进的一部分,文中试图分析影响同步器静态挂挡力变化的结构或尺寸因素,研究单体同步器静态挂挡力和挂挡行程的理论曲线,为后续变速器静态换挡力和行程曲线分析以及动态换挡性能分析改善奠定基础。
1 同步器挂挡过程
某典型锁环式同步器的挂挡过程如下:(1)滑动齿套离开空挡位置,通过柱塞带动滑块轴向移动,直到同步器与齿轮安装间隙消失,同步侧为并紧状态;(2)预同步阶段。同步环旋转1/4周节(拨环),进入预锁止位置;(3)同步阶段。滑套上的齿与锥环的齿锁止面相接触,锥面间产生摩擦力矩;(4)同步结束,摩擦力矩降为0,同步环在拨环力矩作用下,回转1/4节,滑套穿过同步环;(5)滑套与结合齿圈的齿相结合,挂挡结束[4]。
如图1和图2所示,根据前面所述同步器挂挡过程,具体分析各步骤下轴向位移值和所对应的尺寸参数,为确定力与行程曲线图横坐标节点奠定基础。
某变速器主箱锁环式同步器相关参数如下:挂挡行程L= 13.5 mm,接近距离t=0.52 mm,滑块间隙δ1=1.33 mm,后备量δ3=2.2 mm,单边安装尺寸比并紧尺寸大s=0.5 mm;结合齿圈结合齿倒角100°,分度圆处倒角轴向宽度f=2 mm。分析后得到同步器挂挡过程中滑动齿套位移如表1所示,以同步器对称中心为0位移。
接近距离t与滑块间隙δ1、嵌入量δ2、锁止结合齿花键参数及锁止角参数等有关,可用二维和三维作图法得到;滑动齿套与结合齿圈花键倒角面接触点的准确位置也可用类似方法得到。

表1 滑套位移关键位置
2 挂挡力理论分析
锁环式同步器滑动齿套典型顶销槽型结构如图3所示,以滑套为研究对象,分析其在力P的作用下,3处槽型结构越过弹簧所顶柱销进入助推斜面完成挂挡的整个过程。考虑到挂挡行程L较短,认为整个过程为匀速运动,即假设没有加速度影响,挂挡方向(横向)力平衡。
2.1同步器压簧及柱销施加反力
相关参数如下:同步压缩弹簧刚度系数 k(=4.08 N/mm),安装载荷F0(=26.5 N);静摩擦因数μ=0.15,动摩擦因数μ′=0.12。图3所示,滑套带动柱销弹簧走完间隙,到达预锁止状态(距离锁止位置还有接近距离)时,已有行程1.83 mm,设为相对位移零点。此前滑套所受横向挂挡力为重力等引起的摩擦力,接近0;在滑套相对柱销启动时,通过受力分析得到挂挡力计算式为:
式中:α为滑套槽斜面倾角(α=45°);摩擦力f摩启动前为静摩擦力,摩擦因数μ=0.15;N为柱销给滑套的压力;P为滑套上所求挂挡力。代入各参数值得到滑套与柱销相对滑动瞬间,即相对位移为0时的挂挡力P=91.5 N。
之后,如图4所示,状态A~E为锁环式同步器挂挡过程中滑套受柱销作用力变化,图中xa为相对于图3位置所指,加上同步器预锁止前的行程1.83 mm即为绝对位移。结合表1对挂挡行程关键节点的分析,分别计算图示过程中的挂挡力。
0A段:滑套挂挡相对位移0~1 mm,此段位移跨越第1节同步器挂挡过程的第2、3、4阶段,滑套受柱销力如图4(a)所示,则挂挡力计算式为:
式中:ya=xa,α=45°,摩擦因数μ=0.12。将xa=0.52 mm和x′a=1 mm代入得到对应挂挡力Pa=96.2 N和P′a=102.7 N。
AB段:滑套挂挡位移1~3.5 mm,此段位移跨越前面同步器挂挡过程的第4、5阶段,滑套受力终点如图4(b)所示,在AB行程之间,滑套受力如图5所示,则挂挡力计算式为:
式中:位移 xb=Rsin45°-Rsinα,压缩量yb=Rcosα-Rcos45°;ya=1 mm,动摩擦因数μ=0.12。考虑α从45°~0°变化,挂挡力与位移曲线关系如图6所示,滑套尖点在柱销滑动时,曲线接近线性变化。
BC段:滑套挂挡位移3.5~5.01 mm,此段位移位于前面同步器挂挡过程的第5阶段,滑套受力如图4(c)所示,压力无横向分量,力P仅需要平衡滑动摩擦力。
将ya=2.1 mm、摩擦因数μ=0.12代入式(5)得Pc= 12.6 N。
CD段和DE段:滑套挂挡位移分别为5.01~5.75 mm、5.75~11.67 mm,此段位移位于前面同步器挂挡过程的第5阶段,终点滑套受力如图4(d)、(e)所示,经过点C进入CDE段后,压力N和滑动摩擦f摩横向分量方向与P相同,对同步器静态挂挡来说,此时力P为0,同步器即自行完成后面行程。考虑动态挂挡时的通用性,文中认为N与f摩换向后,P反向,为负值,确为线性过渡。在D和E位置,横向力P分别为:
将yd、ye、α=25°、摩擦因数μ=0.12代入得到:位移xd=5.75 mm时,对应挂挡力Pd=-58.8 N;位移xe=11.67 mm时,对应挂挡力Pe=-53.8 N。
2.2同步器外摩擦环施加反力
过程3锁止位置结束后(相对位移0.52 mm,绝对位移2.35 mm),进入穿越后备量的过程4时(此段位移长由滑套齿顶倒角宽度d=1 mm决定),存在同步结束滑套与外摩擦环锁止面相对滑动过程,存在摩擦力横向分量fβ,如图7所示,其中锁止角β=55°,锁止面摩擦因数μβ=0.12
联立公式(3)、(4)和(8),由横向力平衡得到相对位移0.52~1.52 mm(绝对位移2.35~3.35 mm),挂挡力分段计算式见公式(9):
代入xa=0.52、1 mm及xb=1.52 mm(ya同前)得换挡力P分别为:104.9、111.9和45.8 N。
3 理论曲线与试验结果比较
根据前面挂挡过程关键位移分析和分段叠加受力分析计算,整理锁环式同步器滑动齿套从初始位置到挂挡行程走完整个过程中,挂挡力和滑套位移行程的数据如表2所示,曲线图如图8所示。
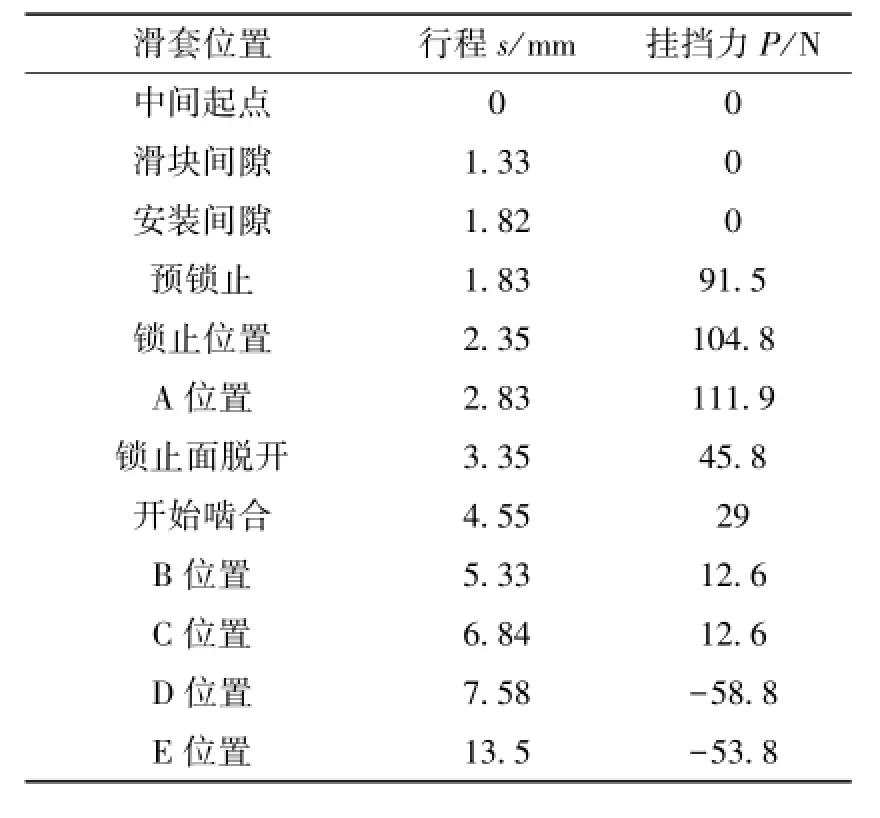
表2 挂挡力与位移数据
从表2和力位移曲线关系上看,同步器单体静态挂挡力锁止位置接近峰值,最大值出现在滑套越过外环、在穿越后备量阶段的A位置,最大值为111.9 N。
为验证以上理论曲线,进行了实测试验。采用图9所示静态挂挡力测试仪及压力传感器得到3套典型锁环式同步器单体挂挡力峰值如表3所示。
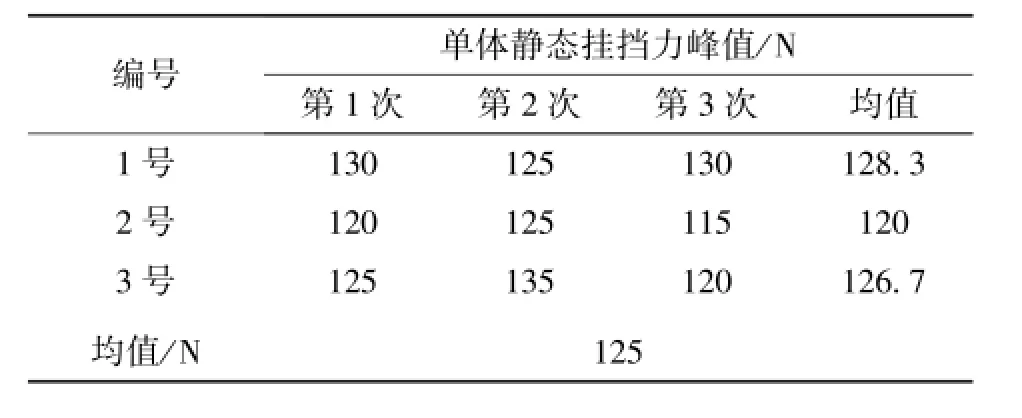
表3 实测同步器挂挡力峰值数据
将理论计算结果峰值与试验结果对比,发现误差为10.48%,考虑摩擦力、零件制造误差、测试误差等因素,该计算结果可信,说明通过挂挡过程受力分析和叠加计算得到的理论曲线具有参考价值。
4 结论
运用分段分析、叠加计算的方法研究换挡过程中与同步器滑动齿套行程相关的结构或尺寸因素,建立了不同位置挂挡力的计算公式,最后得到典型锁环式同步器单体静态挂挡力和挂挡行程的理论曲线,挂挡力峰值与试验测量比较结果表明理论计算准确可信。文中的研究为后续机械式变速器静态换挡力行程曲线分析以及动态换挡性能分析改善奠定良好的基础。具体来看有以下几点结论:
(1)分析同步器实际挂挡过程,分段叠加计算得到换挡力与行程曲线方法可行。
(2)典型锁环式同步器的静态挂挡力峰值位置与动态同步锁止位置吻合,可以指导后续同步器动态性能分析和改进。
(3)空行程(间隙)、锁止面角度尺寸以及滑套柱销接触部分结构尺寸等细节对静态挂挡力的峰值和力位移曲线走势有重要影响,设计需要认真分析考虑。
【1】郭增钢.新一代同步开发与应用[J].汽车工程师,2011(2):58-60.
【2】陈习江.变速器静态换挡力的分析与研究[J].安徽科技,2011(11):26.
【3】刘修珂.汽车手动变速器换挡品质及同步时间测试研究[D].武汉:武汉理工大学,2011:3-5.
【4】陈家瑞.汽车构造:下册[M].北京:机械工业出版社,2009:55-59.
Analysis for Static Shift Force and Displacement Curve of Synchronizer
ZHANG Gang,QIU Huipeng
(Shaanxi FAST Auto Drive Engineering Research Instute,Xi'an Shaanxi 710119,China)
Structure and dimensions of block synchronizer which may had influence on displacement of clutch sleeve were analyzed;shift forces were calculated for different position and subsections;then static shift force and displacement curves for single typical block synchronizer were got.Comparing with test data,theoretical calculation results are accurate and credible;maximal shift force position for the typical block synchronizer is same with dynamic locking position.
Block synchronizer;Static shift force;Displacement curve
2015-04-21
章刚(1985—),男,硕士,研究方向为汽车变速器关键零部件。E-mail:zhanggang@chinafastgear.com。

