复杂网络聚类算法综述
李建 郑晓艳
摘要:随着复杂网络应用的日益广泛,发现复杂网络簇结构的复杂网络聚类算法越来越多。这导致在实际应用中根据实际的复杂网络结构选择合适的聚类算法成为一大难题。针对这种情况,根据复杂网络聚类算法的求解策略,通过介绍各个经典的复杂网络聚类算法的基本原理、实现步骤以及优缺点,对这些算法进行归类和比较,得出了它们对应的更好的适用范围,有助于在复杂网络聚类分析中选取合适的算法解决问题,为相关领域的研究者提供了参考。
关键词:复杂网络; 簇结构;聚类
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2015)05-0037-05
Survey of Complex Network Clustering Algorithms
LI Jian, ZHENG Xiao-yan
(College of Information Technology Engineering, Tianjin University of Technology and Education, Tianjin 300222, China)
Abstract:Complex network clustering algorithms which aim to discover network communities are increasing along with the wide application of complex networks, so it is hard to select the appropriate clustering algorithm based on the actual structure of complex networks in application. In view of this situation, it classifies and compares the classical complex network clustering algorithms through introducing the basic principle, the implement steps, the advantages and disadvantages as well as the solving strategy of the complex network clustering algorithms. Finally, it gets the better scope of application, which is beneficial to selecting the appropriate algorithms for the complex network clustering analysis and providing a reference for researchers.
Key words:complex network; community structure; clustering
近几年随着复杂网络的发展,现实世界中的各种网络大量涌现,许多复杂系统直接或间接地以复杂网络的形式存在,如社会关系网、新陈代谢网等。网络簇结构(network community structure)是复杂网络最普遍和最重要的拓扑结构属性之一,具有同簇节点相互连接密集、异簇节点相互连接稀疏的特点,复杂网络聚类是为了找到复杂网络中真实存在的全部簇[1]。
研究复杂网络聚类算法有助于挖掘出复杂网络的内在规律、拓扑结构、各类功能以及发展趋势,具有重要的理论意义和广阔的应用前景。在此背景下,本文概述了各复杂网络聚类算法的基本思想、实现步骤和优缺点。
目前,复杂网络聚类算法有两种求解方法,第一种是启发式方法,将复杂网络聚类问题转化成预定义启发式规则的设计问题;第二种是基于优化的方法,通过最优化预定义的目标函数来计算复杂网络的簇结构从而将复杂网络聚类问题转化成优化问题[2]。
1 启发式方法
典型的启发式复杂网络聚类算法有hyperlink induced topic search(HITS)算法[3]、maximum flow community(MFC)算法[4]、Girvan-Newman(GN)算法[5]及其改进、Wu-Huberman(WH)算法[6]、clique percolation method(CPM)算法[7]、finding and extract-ing communities(FEC)算法[8]、基于标签传播的网络聚类算法和基于仿生计算的网络聚类算法。以上算法都是利用某种直观假设,可快速找到大多数复杂网络的最优解或近似最优解,但是却不能保证对于任意网络都可以得出很好的解。
1.1 HITS算法
1999年,Kleinberg等人提出了HITS算法[3],认为web页面有权威性(Authority)和枢纽性(Hub),取值依次用 和 表示。HITS算法利用页面之间的引用链来发现隐含在WWW中的网络簇结构,计算简单且效率高,已被广泛应用。HITS算法的实现步骤简述如下:(1)选取根集; (2)构造基集; (3)构造邻接图; (4)迭代得出结果。
HITS算法虽然能很好地描述Web的组织特点,但易出现主题漂移现象,导致不同的查询算法要重新运行,开销过大,因此HITS算法不能用于实时系统。
1.2 MFC算法
2002年,GW.Flake 等人提出了MFC算法[4],它的提出思想是簇内边的密度远远大于簇间边的密度。簇间连接构成网络“瓶颈”,其容量决定最大流量,可由最小截集计算得出,反复识别、删除簇间连接,可以逐渐分离网络簇,当前计算最小截集最快需要
1.3 GN算法及其改进
2002年,Girvan和Newman提出了著名的GN算法[5]。GN算法以簇间连接的边介数应大于簇内连接的边介数为启发式规则,不断删除边介数最大的边,最终把整个网络划分成若干个网络簇[1]。边介数定义成
通常在聚类数目已知的情况下应用GN算法,该算法最大的缺点是计算速度慢、开销大,时间复杂度很高,所以其不适合处理大规模的网络。针对该问题,学者们对GN算法进行改进,而后提出了采用节点集的GN算法和自包含GN算法等。
1.4 WH算法
2004 年,Wu和 Huberman结合物理学知识,提出了WH算法[6],在该算法中,整个网络被看作一个电阻网络,每条边被看作一个电阻,位置不同的节点电位势不同。选取位于不同簇中的两个节点作为正负极,根据簇内电阻远远小于簇间电阻得出异簇节点位势不同而同簇节点位势近似相同[6]。WH算法利用最大位势差来识别网络簇,该过程可在线性时间内完成,但是WH算法往往需要大量难以获取的先验知识。
1.5 CPM算法
复杂网络的快速发展使更多的研究者投入到重叠网络的研究。2005年,Palla等人提出了CPM算法[7],他们认为网络簇可以看作由若干重叠的团组成,通过搜索相邻的团可检测网络的簇结构。CPM算法的实现步骤简述如下:(1)确定参数
虽然CPM算法是首个可以识别重叠网络簇结构的算法,但是参数
1.6 FEC算法
2007年,Yang等人针对符号网络聚类问题,在Markov随机游走理论的基础上提出了FEC算法[8],符号网络包含正、负两种关系,在复杂系统中普遍存在。FEC算法的基本假设是:如果从网络中任意一个簇出发进行随机游走,结果到达起始簇内节点的概率应大于到达剩余簇中节点的概率[9]。在此基础上,FEC算法的实现步骤简述如下:(1)任选目的节点
随机游走步长
1.7 基于标签传播的网络聚类算法
2002年,Zhu等人提出了LPA算法[10],其使用已被标记的节点标签信息来预测未被标记的节点标签信息。LPA算法的实现步骤简述如下[11]:(1)构造边权重矩阵,得出数据之间的相似度;(2)计算节点之间的传播概率;(3)定义标注矩阵;(4)根据(2)、(3)更新概率分布;(5)更新初始矩阵,重复(4),直到收敛。
2007年,Raghavan等人提出RAK算法[12],第一次把LPA的思想应用到复杂网络聚类中。
2009年,Leung等人[13]通过研究发现LPA算法有很大潜力处理大规模网络的聚类问题。
2009年,Barber对LPA算法的目标函数进行修正,提出了带约束的LPAm算法[14],改善了LPA算法的聚类性能。
2010年,Liu等人考虑到LPAm算法易陷入局部最优解,在层次贪婪算法MSG和LPAm算法的基础上,提出了LPAm+算法[15],进一步改善了标签传播类算法的聚类性能。
1.8 基于仿生计算的网络聚类算法
2007年,Liu等人在研究蚂蚁行为的基础上提出了蚁群聚类算法[16],该算法应用于邮件社会网络。
2010年,刘大有等人在Markov随机游走的基础上提出了RWACO算法[17],之后对RWACO算法进行了改进。
2011年,公茂果等人提出了密母算法[18],该算法可以有效探测网络中的层次簇结构。
2012年,何东晓等人提出多层蚁群算法(MABA算法)[19],该算法可发现网络中的层次簇结构,其实现步骤简述如下:(1)运行其子算法,发现网络簇结构;(2)把簇看作节点,簇间链接看作加权边,构建上层网络,并将子算法用于此网络;(3)重复以上步骤,直到模块度
2 基于优化的算法
在基于优化的复杂网络聚类算法中,两种经典的代表算法是谱聚类算法和局部搜索算法。
2.1 谱聚类算法
谱聚类算法基于谱图理论,把各个样本数据视为顶点
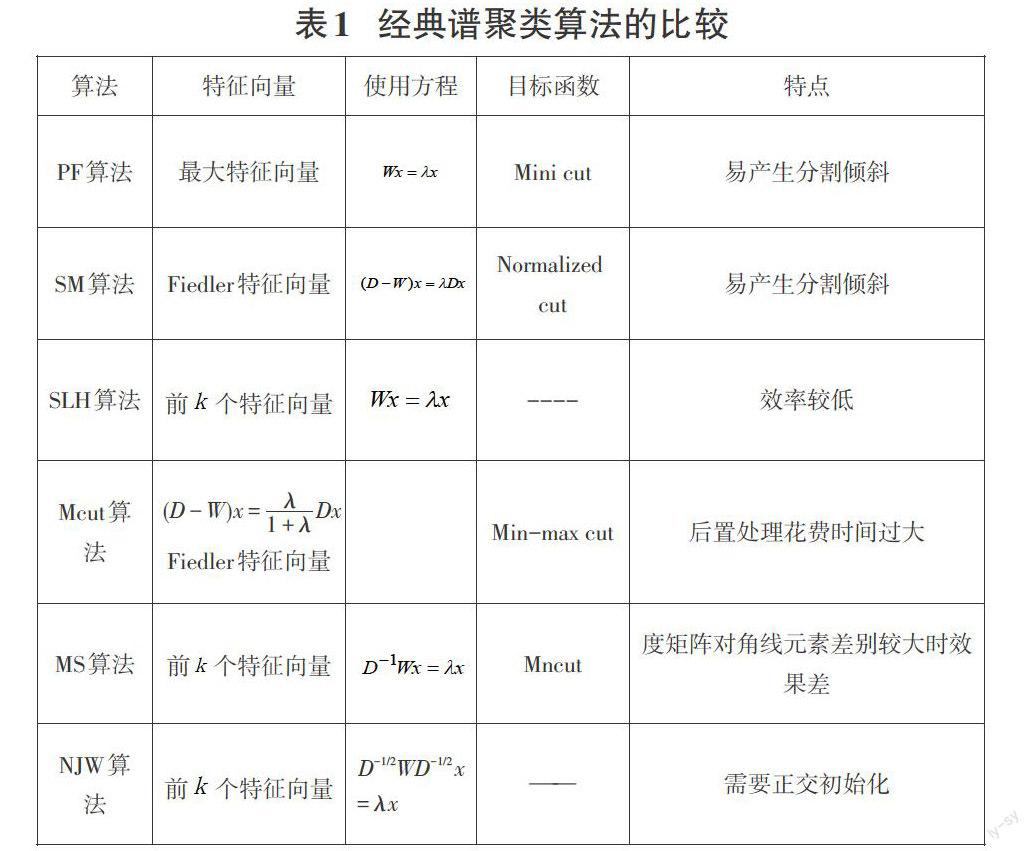
经典的二路谱聚类算法有Freeman和Peron提出的PF算法[21]、Shi和Malik提出的SM 算法[20]、Scott和Languet Higgins提出的SLH算法[22]、Kannan R和Vempala S提出的KVV算法[23]以及Ding提出的Mcut算法[24]。经典的多路谱聚类算法有Ng,Jordan等人提出的NJW算法[25]以及Meila提出的MS算法[26]。上述典型算法的比较,如表1所示。这些算法的实现步骤都可用以下三个重要步骤表示:(1)构建表示样本集的矩阵[Z];(2)计算[Z]的前
谱聚类算法可发现不规则形状的网络簇,应用于各种形状的样本空间,且结果收敛于全局最优解。近几年谱聚类算法的研究虽有了一定的成果,但仍有以下需要解决的问题:(1)如何构造相似矩阵[W];(2)如何处理特征向量;(3)如何自动确定聚类数目;(4)如何选取Laplacian矩阵;(5)如何运用到大规模学习问题中。
2.2 局部搜索算法
目前,比较经典的基于局部搜索优化技术的复杂网络聚类算法有Kernighan-Lin(KL)算法[27]、快速Newman(FN)算法[28]、Guimera-Amaral(GA)算法[29]、Fast Unfolding Algorith-m(FUA)[30]和Fast Network Clustering Algorithm(FNCA)[17]。
2.2.1 KL算法
1970 年,Kernighan和Lin提出KL算法[27],该算法是一种基于贪婪思想的优化算法,其基本思想是引入增益函数
2.2.2 FN算法
2004年,Girvan和Newman提出网络模块度
FUA算法
2008年,Blondel等人基于局部优化和层次聚类提出了FUA算法[30],该算法的计算时间优于其他大多数的网络聚类算法,尤其对于稀疏网络,其时间复杂度为
FNCA算法
2011年,刘大有等人提出了FNCA 算法[17]。他们在模块度
2.2.3 基于优化的复杂网络聚类算法的分析
基于优化的网络聚类算法还有很多,这些算法的优化目标大多是最大化
3 其他复杂网络聚类算法
除上述主要的网络聚类算法外,还有其他的网络聚类算法。如Gudkov等人提出的基于动力学的演化算法[32];Bagrow和Bollt提出的局部聚类算法—L-shell算法[33];Papadopoulos等人提出的和L-shell算法相似的桥边界算法等[34]。
4 结束语
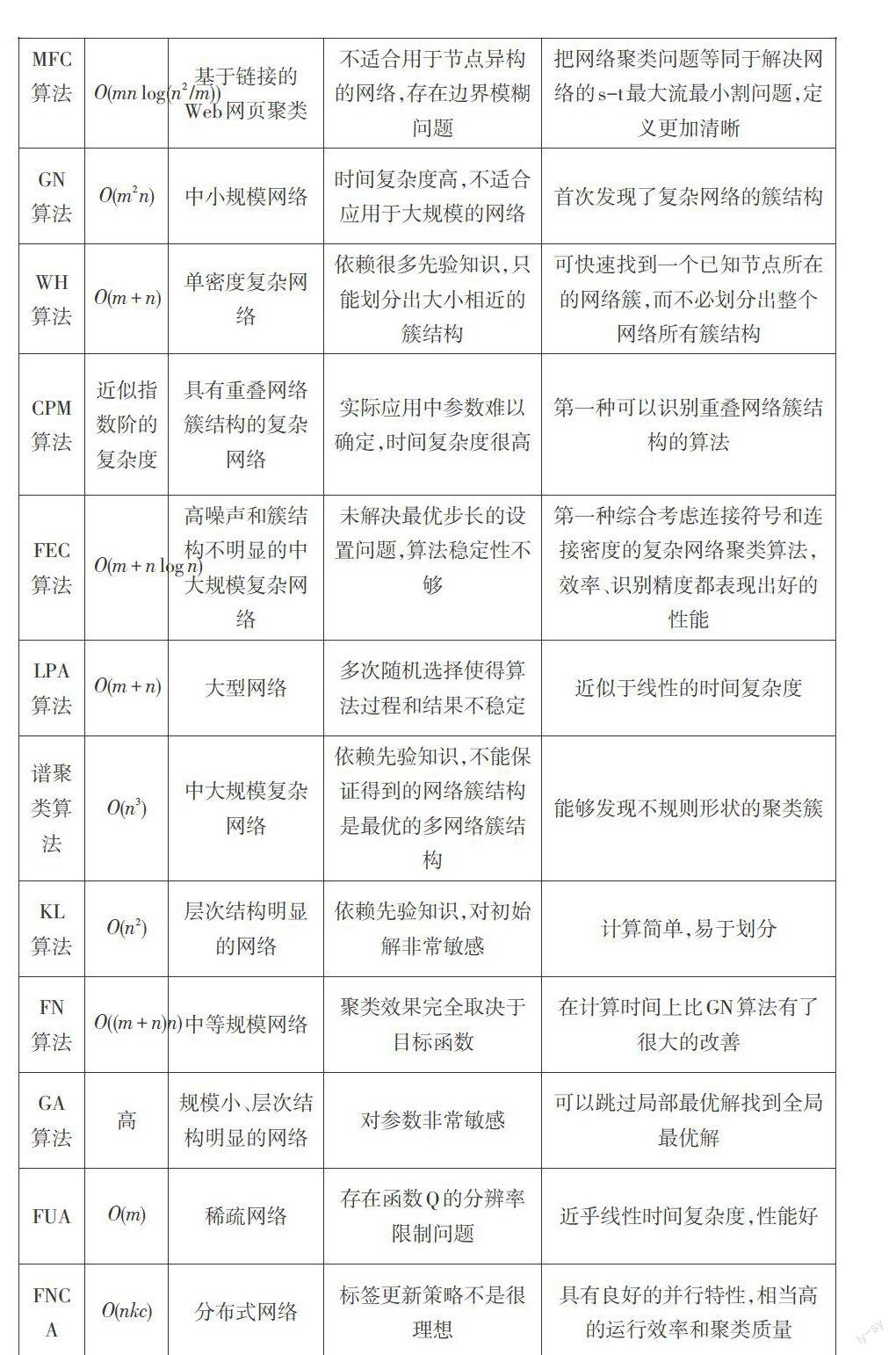
本文主要对几个经典的复杂网络聚类算法进行了综述,介绍了它们的基本原理、实现步骤以及优缺点。现将上述典型的复杂网络聚类算法的性能做比较如表2所示,其中
尽管复杂网络聚类算法已经取得了一些成果,但是还有一些需要解决的问题,如:(1)关于网络簇结构,目前还没有一个明确客观的定义,只能借助目标函数或启发式规则识别网络簇结构。这样会使刻画的网络簇结构与真实存在的网络簇结构存在一定的偏差,因此,我们亟待解决的问题之一是能否以复杂网络的自身属性为依据,得出一个明确客观的理论来刻画复杂网络簇结构。(2)簇结构具有重叠性和层次性,它们之间存在“冲突”,大部分算法只能解决一方面。(3)现有的聚类算法都有一定的限制,不能同时具有效率高、不依赖先验知识、对参数不敏感、聚类结果精确且适用于大规模数据集等优点。因此,我们需要研究出一种复杂网络聚类算法,该算法能够在没有先验知识的条件下快速刻画出真实的网络簇结构。
参考文献:
[1] 杨博,刘大有.复杂网络聚类方法[J].软件学报,2009,20(1):54-66.
[2] 周斌,程慧.基于贪婪算法的符号网络中社团结构快速发现算法[J].大众科技,2009,(12):48-49.
[3] Kleinberg JM.Authoritative sources in a hyperlinked environment[J].Journal of the ACM,1999,46(5):604-632.
[4] Flake GW,Lawrence S,Giles CL,et al.Self-Organizationand identification of Web communiti-es[J].IEEE Computer,2002,35(3):66-71.
[5] Girvan M,Newman MEJ.Community structure in socialland biological networks[J].Proc.of the National Academy of Science,2002,9(12):7821-7826.
[6] Wu F,Huberman BA.Finding communities in linear time:A physics approach[J].European Phy-sical Journal B,2004,38(2):331-338.
[7] Palla G,Derenyi I,Farkas I,et al.Uncovering the overlapping community structures of com-plex networks in nature and society[J].Nature,2005,435(7043):814-818.
[8] Yang B,Cheung W K,Liu J.Community mining from signed social networks[J].IEEE Trans.on Kn-owledge and Data Engineering,2007,19(10):1333-1348.
[9] 陈登峰.多属性无向加权图上的聚类方法研究[D].黑龙江:黑龙江大学,2011.
[10] Zhu Xiao-Jin,Ghanramani Z.Learning from labeled and unlabeled data with label propagati-on [R].Pittsburghers:Carnegie Mellon U-niversity,2002.
[11] 罗秋滨.标签传播算法在社会网络中的应用研究[J].智能计算机与应用,2013(3):37-43.
[12] Rahavan U N,Albert R,Kumara S.Near linear time algorithm to detect community structures in large-scale networks[J].Physical Review E,2007,76(3):036106.
[13] Leung I X Y,Hui P,Liò P,et al.Towards real time community detection in large networks[J].Physical Review E,2009,79(6):066107.
[14] Barber M J,Clark J W.Detecting network communitiesby propagating labels under constrain-ts[J].Physical Review E,2009,80(2),026129.
[15] Liu X,Murata T.Advanced modularity-specialized labelpropagateon algorithm for detecting communities in networks[J].Physica A,2010,389(7):1493-1500.
[16] Liu Y,Wang Q X,Wang Q,et al.Email community detection using artificial ant colony clust-ering[C]//Proc of Joint the 9th Asia-Pacific Web Conf and the 8th Int Conf on Web-Age Information Management Workshops.Berlin:Springer,2007,287-298.
[17] 金弟,杨博,刘杰,等.复杂网络簇结构探测—基于随机游走的蚁群算法[J].软件学报,2012,23(3):451-464.
[18] Gong M,Fu B,Jiao L,Memetic algorithm for community detection in networks[J].Physical Re-view E,2011,84(5):056101.
[19] He D,Liu J,Liu D,et al.An ant-based algorithm with local optimization for community det-ection in large-scale networks[J].advances in Complex Systems,2012,15(8):1250036-1-26.
[20] Shi J,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern An-alysis and Machine Intelligence,2000,22(8):888-905.
[21] Perona P,Freeman W T.A factorization approach to grouping[C].In 5th European Conf on C-omputer Vision Proceedings,1998,1:665-670.
[22] Scott G L,Longuet-Higgins H C.Feature grouping by relocalization of eigenvectors of theproximity matrix[C].Proc.British Machine Vision Conference.1990:103-108.
[23] Kannan R,Vempala S,Vetta A.On clusterings:good,badand spectra1[J].Journal of ACM,2004,51(3),497-515.
[24] Ding C,He X F,Zha H Y,et a1.A min-max cut algorithm for graph partitioning and data clu-stering[C]//Proceedings of IEEE International Conference on Data mining.San Jose:IEEE,2001:107-114.
[25] Ng A Y,Jordan M I,Weiss Y.On spectral clustering: Analysis and an algorithm[J].Proceedi-ngs of Advancesin Neural Information Processing Systems.Cambridge,MA:MIT Press,2002,14:849-856.
[26] Meila M,Shi J.Learning segmentation by random wal-ks[C]//Advancesin Neural Information Processing Systems,Cambridge,2000:873-879.
[27] Newman MEJ.Detecting community structure in networks[J].European Physical Journal B,2004,38(2):321-330.
[28] Newman MEJ.Fast algorithm for detecting communitystructure in networks [J].Physical Rev-iew E,2004,69(6):066133.
[29] Guimera R,Amaral LAN.Functional cartography of complex metabolic networks[J].Nature,2005,433(7028):895?900.
[30] Blondel V D,Guillaume J L,Lambiotte R,et al.Fast unfolding of communities in large netw-orks[J].Journal of Statistical Mechanics:Theory and Experiment,2008,(10):10008.
[31] Newman MEJ,Girvan M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69(2):026113.
[32] Gudkov V,Montealegre V,Nussinov S,et al.Communitydetection in complex networks by dynam-ical simplexevolution[J].Physical Review E.2008,78(1):016113.
[33] Bagrow J P,Bollt E M.Local method for detecting communities[J].Physical Review E,2005,72(4):046108.
[34] Symeon Papadopoulos AS,Yiannis Kompatsiaris,Athena Vakali,etal.Bridge bounding a local approach for efficient community discovery in complex networks[J].Physics and Society,2009.

