中继下基于特征子矩阵的干扰对齐优化算法

袁莉莉，周小平

(上海师范大学信息与机电工程学院，上海200234)

0 引言

在现代无线通信中，随着用户数的增加，用户之间的同道干扰成为影响无线通信质量的重要瓶颈，干扰对齐［1-3］作为协作多点传输技术是抑制同道干扰的最有效的手段，相对于传统的干扰抑制技术在系统容量和自由度方面已经表现出了明显的优势．近几年一直是研究的热点问题．

文献［4］和［5］指出两用户干扰信道的容量域可通过先译码干扰信号，从接收信号中把干扰信号删除再获取期望信号的方法获得，但是多用户的容量域无法直接获得一般解．

文献［6］分别提出在MIMO干扰信道下对线性预编码和接收滤波器的干扰对齐算法，发送端预编码的求法是利用特征波束成型的方法对齐干扰的次流，减小在接收端的干扰矢量;接收端干扰抑制矩阵的求法是基于最小干扰泄露的迭代算法，仿真结果表明所提出的算法相对于传统干扰对齐算法提高了系统平均速率．文献［7］分析了频率域的干扰对齐算法，信号通过子载波分组的方式在信道中传输，通过数值仿真表明分组传输方式比频率复用在系统平均速率上要高．文献［8］在发送端两天线，中继多天线的X信道场景下，提出一种干扰对齐方案，通过仿真证明文中所提方案可以取得四分之三的自由度并提高了分集增益．文献［9］在K用户MIMO干扰信道系统中提出一种低复杂度的分布式干扰对齐算法，通过对用户K的干扰协方差矩阵进行排序QR分解算法，选出酉矩阵Q最后的dk列作为用户近似的干扰抑制滤波矩阵，仿真结果表明，相比于传统干扰对齐方案系统复杂度明显降低．文献［10］提出在多天线中继干扰信道中，中继辅助干扰对齐算法，该算法通过联系均方误差和可达到的速率解决了系统最大速率的问题，仿真结果表明，文中所提算法在系统总速率和复用增益上均有明显提高．

本文作者分析整个中继网络系统中所有用户的干扰问题，针对MIMO双向中继模型系统中，用户对之间发送的数据流是非对称的，推导出用户对和中继之间的天线数分配关系，以便满足对齐信号并抑制干扰的可行性条件．在经典的最小干扰泄漏迭代算法基础上提出一种优化方案，基于特征子矩阵准则，综合考虑系统中所有用户的利益来为每个用户选择最优的预编码矩阵，使得其他用户的信号在中继端对齐到干扰信号子空间;再利用分布式迭代算法，逐一迭代出每个用户的最优干扰抑制矩阵，以达到在用户端消除其他用户干扰的目的，从而优化整个双向中继网络系统．通过仿真结果表明，所提优化方案针对MIMO非对称信道模型，不仅优化了整个系统的性能，而且提高了系统传输速率．

1 系统模型及双向中继干扰对齐的原理分析

1．1 系统模型

研究双向中继下且中继的工作方式为放大转发，4用户对干扰信道网络其系统模型如图1所示．

图1 系统模型图

在第一个时隙，中继接收到的信号为:

接收端k′接收到的信号为:

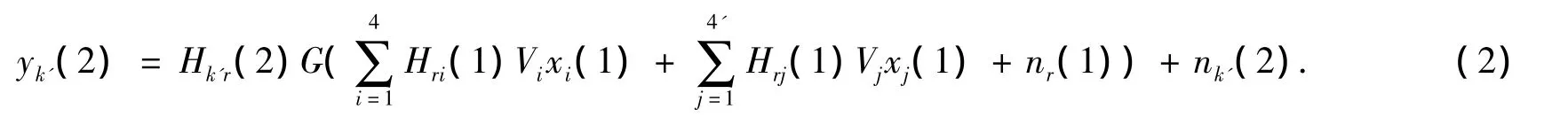
接收端k′消除自我干扰信号:

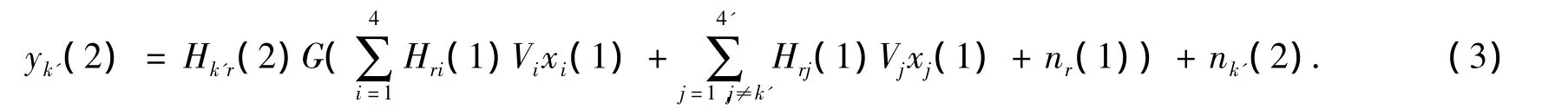
在(1)式和(2)式中，xi(k)(k=1，2)表示发送端i在时隙k时发送的原始信号;nr(1)为中继在时隙1时接收端的加性高斯白噪声;Vi是用户i的预编码矩阵;G为中继信号放大因子;Hri，Hrj，Hk′r分别表示发送端i到中继，发送端j到中继，中继到接收端k′的信道矩阵．

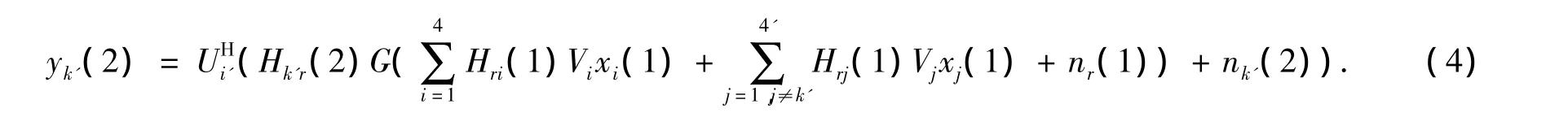
1．2 双向中继网络中干扰对齐的原理

本节分析了双向中继下干扰对齐的原理，其过程包含信号对齐和干扰抑制两个阶段．为了充分利用中继接收信号空间，通过预编码技术将发送用户与目的用户的发送数据流对齐到同一个di维的信号空间．

由图2可知，双方将信号发送到中继并将相对应的收发端对齐到相同的信号维度空间，预编码矩阵需满足收发双方条件:

图2 中继节点的信号对齐

式(5)表明收发双方构成了矢量空间的交集．中继节点收到总共数据流的个数为因此中继节点的天线数应满足为求得预编码矩阵设:

在广播阶段，中继节点对接收信号进行简单的线性放大再将其转发出去，接收端具体的信号处理过程如图3所示．

图3 用户端的信号处理过程

从图3中可知，接收端用户先减去自身发送信号，再经过干扰抑制矩阵，将其他用户的干扰滤除．

2 干扰对齐优化算法

2．1 预编码的设计(基于特征子矩阵的干扰对齐预编码优化方法)

在经典干扰对齐方法［11］中，约束条件并没有用到发送端到期望接收端的信道矩阵Hii(i=1，2，3，4);同时预编码矩阵是随机选择的．因此，经典干扰对齐在容量方面是次优的．

针对经典干扰对齐方法中存在的不足，提出利用发送端的信道状态信息Hii从预编码矢量集合中选取一组与最优特征子信道匹配的预编码矢量来传输数据，使发送端的有用信号在传输中选取信道质量最好的一组特征子信道进行传输，增加整个系统的容量．

本算法:首先，对本用户的信道 Hri(i=1，2，3，4)，Hi′r(i=1′，2′，3′，4′)做奇异值分解(SVD):

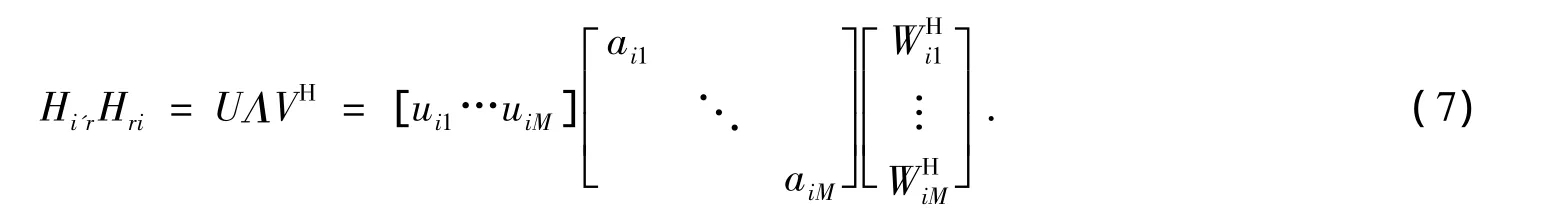
其中，Λ表示奇异值由大到小组成的对角矩阵，对应的奇异值为aim(i=1，2，3，4;m=1，…，M);U和V分别表示奇异值对应的左右奇异矢量组成的矩阵，其对应的左右奇异矢量分别为uim(i=1，2，3，4;m=1，…，M)和 wim(i=1，2，3，4;m=1，…，M);i表示用户下标，m 表示奇异值由大到小排列的下标．wim(i=1，2，3，4;m=1，…，M)代表用户i中信道质量最好的M/2个特征子信道．

在发送端i选择M/2个最优特征子信道进行传输，就是在用户i集中的预编码矢量集合中选择M/2个预编码矢量，使得其与M/2个最优特征子信道内积之和最大，即为所求预编码矩阵．以wim(i=1，2，3，4;m=1，…，M)代替 M/2个最优特征子信道进行传输，具体可表示为

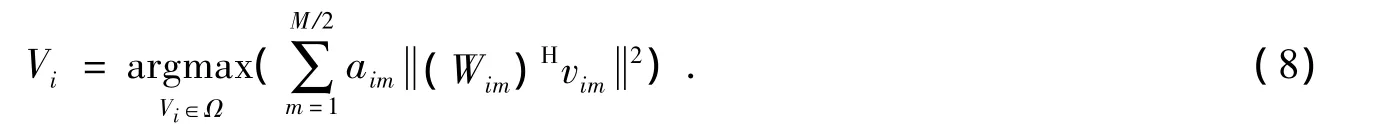
其中vim表示用户i的预编码矩阵的第m列;Vi∈Ω表示Vi满足约束条件．同时，考虑到不同特征子信道wim对最终预编码矢量影响权重的不同，采用其对应的奇异值aim作为权重因子．

在K=4的通信场景下，为了挑选最优的一组特征子信道进行传输，需要满足:

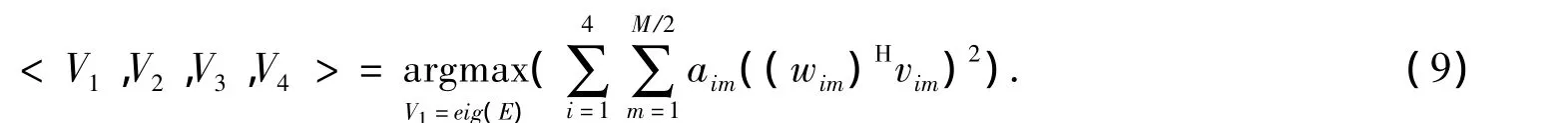
其中 V1，V2，V3，V4满足 span(Hr，iVi)=span(Hr，i′Vi′)，＜ V1，V2，V3，V4＞ 表示 4 用户的预编码矩阵的组合．同理可以求得 1′，2′，3′，4′的预编码矩阵．

2．2 干扰抑制矩阵的求法

(1)随机选择预编码矩阵 V1，V2，V3，V4且满足 Vi(i=1，2，3，4)可逆;

(2)开始迭代;

(4)计算用户i′接收端的干扰抑制矩阵Ui′=vd［Qi′］，即其最小d个特征值对应的特征向量;

(5)根据信道的互易性，变换上下行通信链路方向，令V→i′=Ui′，重复过程(3)，可以得到每个发送端的干扰协方差矩阵

(8)重复过程(3)至(7)，直到收敛．

3 仿真结果及分析

本节对提出的算法、传统分布式迭代算法、传统中继迫零算法以及中继下未采用干扰对齐算法的4种方法进行仿真比较．仿真假设如下:

采用K=4对用户，发送端与接收端都配置3根天线，中继端配置8根天线，发送端数据流个数为di=［1，2，1，2］，接收端数据流个数为 di′=［1，1，2，2］．所有的信道都是独立同分布瑞利信道，每一个信道矩阵都服从独立复高斯分布，零均值单位方差．由图4可以看出，采用所提优化后的干扰对齐算法，系统的总速率得到了显著的改善．

图4 系统平均总速率

4 总结

针对中继网络中用户对间发送的数据流是非对称的，提出满足干扰对齐方案的可行性限制条件，为用户对和中继端配置相应天线数;设计了一种基于特征子信道的干扰对齐优化算法，该算法首先利用特征子矩阵准则，为每个用户设计最优的预编码矩阵，使得信号在中继端对齐;再基于分布式迭代算法，逐一计算出每个用户的干扰抑制矩阵，以达到在用户端消除干扰的目的．仿真结果表明，所提优化算法在该系统模型下，在系统传输速率上有了明显的提高．模型中中继节点的工作方式为半双工，所以下一步对其全双工工作模式的研究也将会成为研究者的热点话题，而该工作模式下如何将干扰对齐技术结合到其中更是表现出巨大的前景．

［1］CHIANG Y H，MA H P．Beamforming based interference cancellation for multiuser MIMO downlink communications:International Conference on Computing，Networking and Communications(ICNC)［C］．Hawaii:IEEE Press，2012．

［2］GOMADAM K，CADAMBE V R，JAFAR SA．A distributed numerical approach to interference alignment and applications to wireless interference networks［J］．IEEE Transactions on Information Theory，2011，57(6):3309-3322．

［3］NING H，LING C，LEUNG K K．Feasibility condition for interference alignment with diversity［J］．IEEE Transaction On Information Theory，2011，56(5):2902-2912．

［4］JAFAR SA．Interference alignment:A new look at signal dimensions in a communication network［J］．Foundations and Trends® in Communications and Information Theory，2011，7(1):1-134．

［5］PARK J，LEE B，SHIM B．A MMSE vector precoding with block diagonalization for multiuser MIMO downlink［J］．IEEE Transaction on Communications，2012，60(2):569-577．

［6］MOHAPATRA P，NISSAR K E，MURTHY CR．Interference alignment algorithms for the K user constant MIMO interference channel［J］．IEEE Transactions on Signal Processing，2011，59(11):5499-5508．

［7］BRANDT R，ASPLUND H，BENGTSSON M．Interference alignment in frequency—A measurement based performance analysis:International Conference on Systems，Signals and Image Processing(IWSSIP)［C］．Vienna:IEEE，2012．

［8］JUNG SK，LEE J W．Interference alignment and cancellation for the two-user X channels with a relay:International Symposium on Personal Indoor and Mobile Radio Communications［C］．London:IEEE，2013．

［9］ZHU Z Y，WANG Z Y，GAO X C，et al．Low Complexity Distributed Interference Alignment for MIMO Interference Channel［J］．Journal of signal processing，2013，29(3):400-404．

［10］TRUONG K T，HEATH R W．Interference alignment for the multiple-antenna amplify-and-forward relay interference channel:Conference Record of the Forty Fifth Asilomar Conference on Signals Systems and Computers(ASILOMAR)［C］．Pacific Grove:IEEE，2011．

［11］CADAMBE V R，JAFAR SA．Interference alignment and degrees of freedom of the k-user interference channel［J］．IEEE Transactions on Information Theory，2008，54(8):3425-3441．