热敏电阻特性的线性化方法

樊　霈，胡　旭，余　俊

（武汉船用电力推进装置研究所，武汉 430064）

热敏电阻特性的线性化方法

樊霈，胡旭，余俊

（武汉船用电力推进装置研究所，武汉 430064）

讨论几种负温度系数（NTC）热敏电阻特性的线性化方法。首先，论文中会介绍一些关于NTC热敏电阻的理论知识和特性曲线。然后，会介绍几种模拟线性化方法。最后，电阻模式线性化和桥梁网络线性化方法将被详细讨论并在软件LTSpice和MATLAB上分别进行模拟，通过实验模拟来验证这两种线性化的实际效果，并进行比较。

NTC热敏电阻线性化

0　引言

热敏电阻是一种特殊的电阻，它的阻值会随着温度变化而发生比较大的改变。热敏电阻基本上是一种陶瓷半导体[1]。这种电阻有两种类型：正温度系数（PTC）热敏电阻和负温度系数（NTC）热敏电阻。PTC热敏电阻会随着温度的升高增加阻值。反之，NTC热敏电阻会随着温度的升高降低阻值。本文将会讨论的是NTC热敏电阻。

NTC热敏电阻通常由一系列金属氧化物组成，比如锰、镍、钴、铁、铜、钛氧化物[1]。而NTC热敏电阻的温度系数特性则是由它所包含的氧化物种类和制造工艺所决定的。相比于其他温度传感器，例如热电偶和铂热电阻温度传感器，热敏电阻有着价格低廉、灵敏度高和准确性高等优点[2]。热敏电阻有着一个很宽广的应用范围，几乎能适用于任何环境。因为它通常有着一个很好的保护镀层。特别是密封在玻璃中的一种热敏电阻，有着非常高的稳定性和准确度[1]。

DO-35封装的热敏电阻是一种常用的温度测量元件。这种封装的热敏电阻经济实用，广泛应用于国内外，多用于汽车系统温度测量和数据处理设备中。本文采用由通用电气测量和控制公司所生产的DO-35封装NTC热敏电阻作为示例来进行讨论与实验。

1　热敏电阻的特性曲线

热敏电阻的阻值与温度的关系是非线性的，可以大概的使用以下方程来表示[3]：

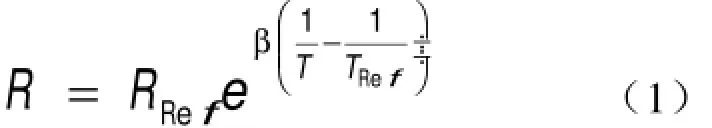
其中T表示温度（K）；TRef表示参考温度，通常是室温(25℃，或者298.15 K)；R是热敏电阻的阻值（Ω）；RRef是在参考温度下的阻值；β是一个校准常量，由热敏电阻的材料所决定，通常是3000 K到5000 K之间。基于通用公司所提供的元器件数据表，此文采用的β值为3960 K±%1，电阻值为10000 Ω在 25℃ 下。通过方程式1和这些参数，可以在 MATLAB中得到热敏电阻的阻值与温度关系曲线：

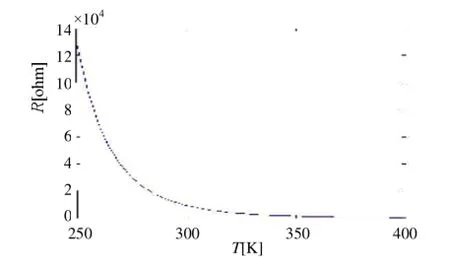
图1　电阻值- 温度特性曲线

从图1可以看出，R-T曲线很明显是非线性的，为了解决这个问题，有几种线性化电路可以使用。

2　基于模拟电路的线性化方法

线性化热敏电阻有很多种方法，以下是几种常用的：

2.1电阻模式

电阻模式线性化方法就是将一个普通电阻和热敏电阻并联起来[4]。这种方法主要用于系统反馈回路和自动增益控制电路。美国微芯科技公司提供了一种简单的例子如图2所示：

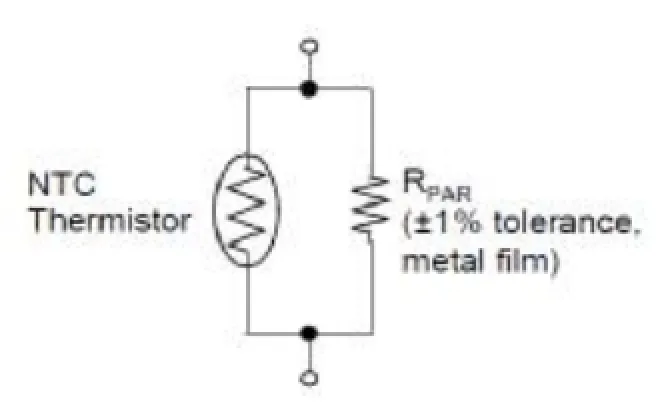
图2　电阻模式线性化电路图[4]

在图2所示电路中，标准电阻用的是公差为±1%的金属薄膜电阻。在室温下（298.15 K），如果标准电阻的阻值等于NTC热敏电阻的阻值，那么热敏电阻特性的线性区域将会以常温为中心，形成一个相对对称的直线[5]。使用这种方法可以改变热敏电阻的测温范围，但不会超过50 K 到100 K之间[6]。

2.2电压模式

在电压模式线性化方法中，热敏电阻将与一个标准电阻和一个参考电压源串联（2.5 V或3 V）在一起[4]。这种串联可以组成一个分压器电路。这种电路可以提供一个相对线性化的输出。微芯科技公司同样提供了一种电路示例如图3所示：

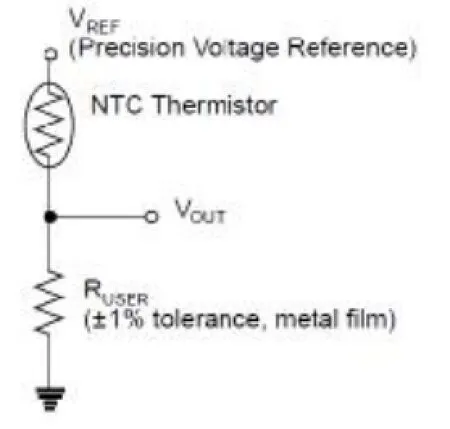
图3　电压模式线性化电路图[4]

使用这种方法也跟电阻模式一样，当标准电阻的阻值等于热敏电阻时，可以形成一个以室温25℃为中心的对称的线性区域。

2.3桥型网络

一种常用的线性化电路如图4所示，这种方法基于惠斯通电桥，可以看作是电阻模式和电压模式的结合。

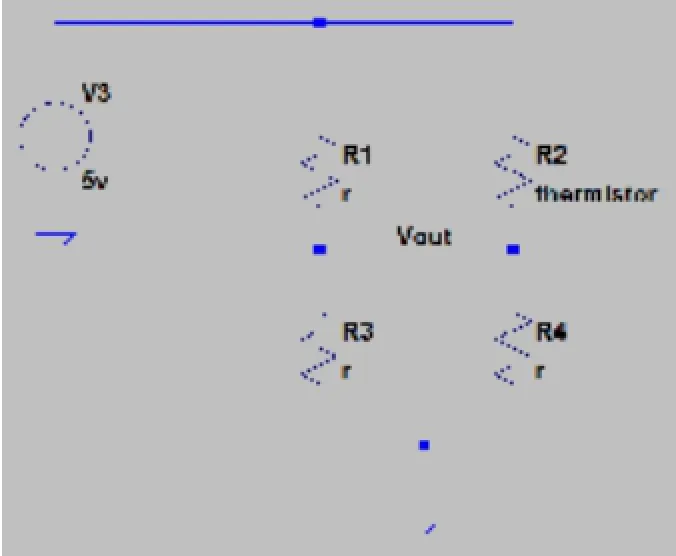
图4　桥型网络线性化电路图

图.5　桥型网络线性化电路图[4]

2.5切比雪夫最优化线性法

这种方法是使用数个同样的热敏电阻基于切比雪夫移动模式来反复减少线性误差直到达到最优[7]。图6所示电路是Carl和Torsten所提供的一种实验电路，具体的方法也可以从他们的论文中找到，由于此方法计算量过大不适用于一般应用，因此并不普及。

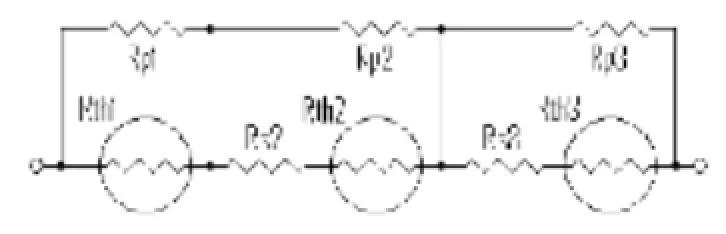
图6　切比雪夫最优化线性法示例电路[7]

3　在软件上进行模拟并分析结果

由于电阻模式和桥型网络这两种线性化方法是最简单并且使用最广泛的两种方法。此论文将会详细讨论并进行模拟来验证两种方法。

3.1使用电阻模式进行线性化

当并联了一个标准电阻后，NTC热敏电阻的R-T特性曲线是一个“S”型（见图7）。当这个“S”曲线的拐点是在工作温度范围的中间时，那么在此温度范围内，可以得到最佳的线性化效果[8]。因此，用来并联的标准电阻的阻值Rp可以通过求指数函数近似数的方法计算出来：

在实际应用中，并联的标准电阻阻值通常等于RRef，所以总电阻Rto为：

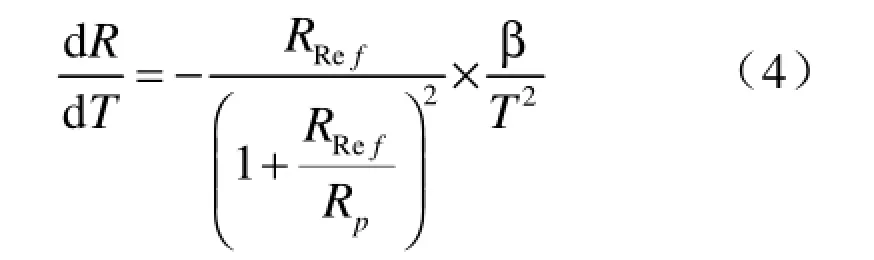
从通用电气测量和控制公司所提供的元器件数据表中[9]，三种热敏电阻的参数被选取进行模拟。三种参数分别为：当 β=3540 K 时，RRef=10000 Ω；当β=3730 K时，RRef=12000 Ω；当β=3960 K时，RRef=20000 Ω 。基于这三对参数，再结合方程1和方程3，在MATLAB中可以得到以下R-T特性曲线：

图7　线性化后的R-T特性曲线

与图1相比，图7的线性化程度得到了很大的提高，并且最佳的线性化区域在室温附近（25℃298.15 K）。通过比较也可以看出，β值低可以提供一个更宽的线性化区域。反之，β值高所提供的线性化区域会变窄，但是灵敏性会更高。

在MATLAB中，只能通过方程式得到一个理论上的结果，接下来，将在LTSpice中进行仿真模拟。

首先，在LTSpice中搭建一个单独的NTC热敏电阻电路，如图8：

此电路中用 R2作为 NTC热敏电阻，RRef=12000 Ω ， β= 3730 K。在温度范围为250 K到500 K时仿真的结果如图9所示：

图8　单独的热敏电阻电路

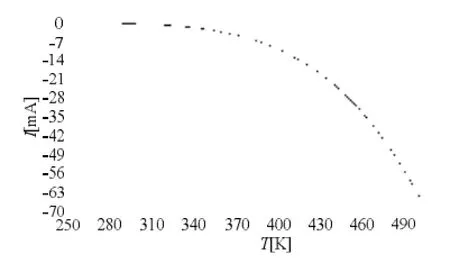
图9　热敏电阻在LTSpice中的特性曲线

在图9中，Y轴表示NTC热敏电阻的电流（mA); X轴是温度（K）。从图9中可以看出单独的 NTC热敏电阻的特性曲线呈现出很明显的非线性化。

接下来，在LTSpice中搭建一个电阻模式线性化电路，如图10。

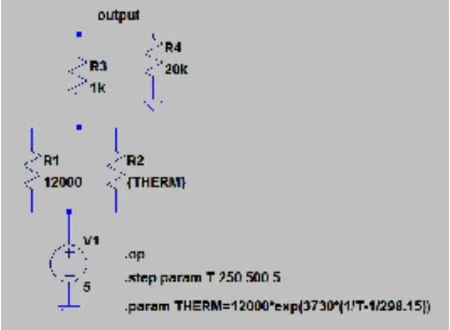
图10　电阻模式线性化电路

图10所示电路中，R1等于RRef=12000 Ω。R3和R4只需要选取适当的值就行，因为它们不会影响线性化，只会影响最大输出范围，此电路中R3=1 K；R4=20 K。仿真结果如图11所示：

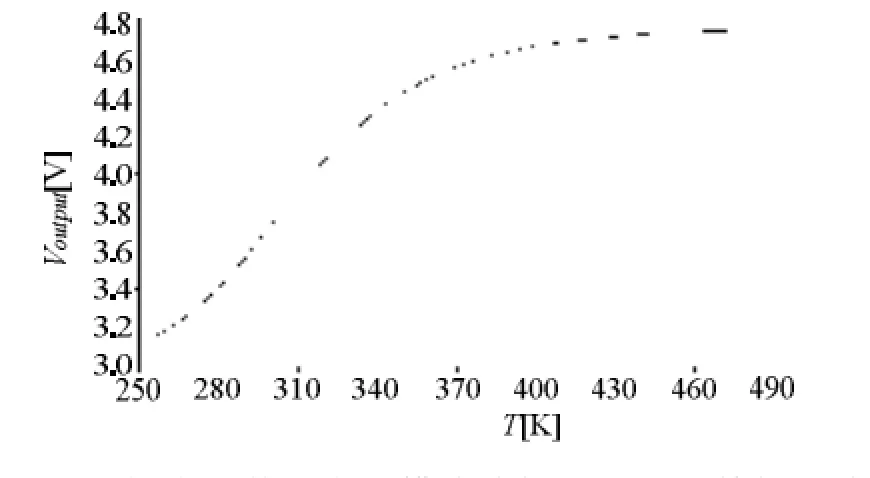
图11　热敏电阻使用电阻模式线性化处理后特性曲线

图11中，Y轴表示输出电压（V），X轴表示温度（K）。与图9相比，经过电阻模式线性化处理后，热敏电阻的线性化程度有了很明显的提高。从图11中可看出，此电路的线性化区域大约在280 K到340 K之间（6.85℃到 66.85℃）。而通常DO-35玻璃封装的NTC热敏电阻工作范围为-40℃到 250℃。因此，与它本身可允许的正常工作区域相比，经此方法处理后的热敏电阻只能得到一个相对较窄的线性区域。并且，从图 11中可以看出，当温度高于370 K后，电路的灵敏性将会大幅下降。

3.2使用桥型网络进行线性化

使用惠斯通电桥来进行线性化处理是在实际应用中使用最多的一种方法。根据惠斯通电桥的原理，可以知道图4中的输出电压为：

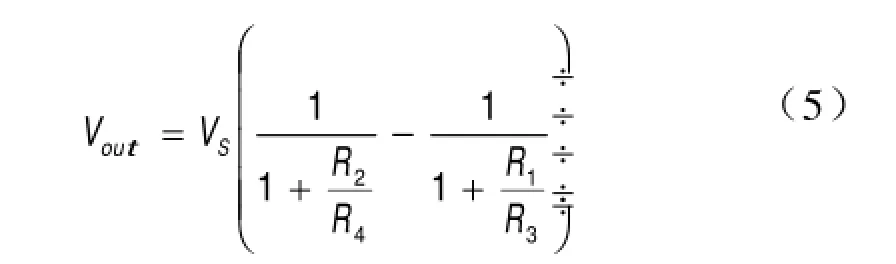
其中R2表示NTC热敏电阻的阻值; R1，R3和R4是固定阻值的电阻，Vs是一个电压源。

为了选取合适的R1，R3和R4的阻值，需要考虑以下两点：第一，电桥的输出电压要是正值，也就是说要达到电桥平衡，由此可得：

第二，此电路的有效工作温度范围要覆盖所选取的热敏电阻的有效工作温度范围（-40℃ ～ 250℃）。

所选取的NTC热敏电阻RRef=12000 Ω ， β= 3730 K。因此R2可由方程1算出。结合方程1和方程5，经计算后，可得：R1=40 kΩ，R3=100 Ω 和R4=850 Ω。 得到这些参数后，再结合方程1和方程5，可以在MATLAB中画出经此方法线性化处理后的热敏电阻V-T曲线：

图12　热敏电阻在MATLAB中的V-T曲线

图12中，Y轴表示电压（V），X轴表示温度（℃），X轴的范围是热敏电阻的工作温度范围-40℃到 250℃。“S”型曲线是热敏电阻经桥型网络方法线性化处理后的特性曲线。可以看出在50℃到 150℃之间，有一个很好的线性化特性。

为了进行仿真模拟，在LTSpic 中搭建图13所示电路：

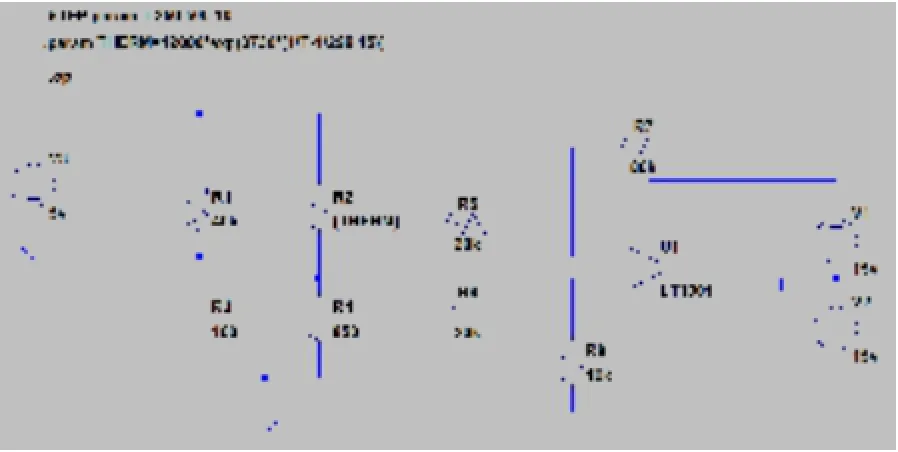
图13　在LTSpice中的桥式网络电路

在图13所示电路中，除了惠斯通电桥外，还搭建了一个简单的放大电路用来放大输出电压。仿真结果如图12所示：

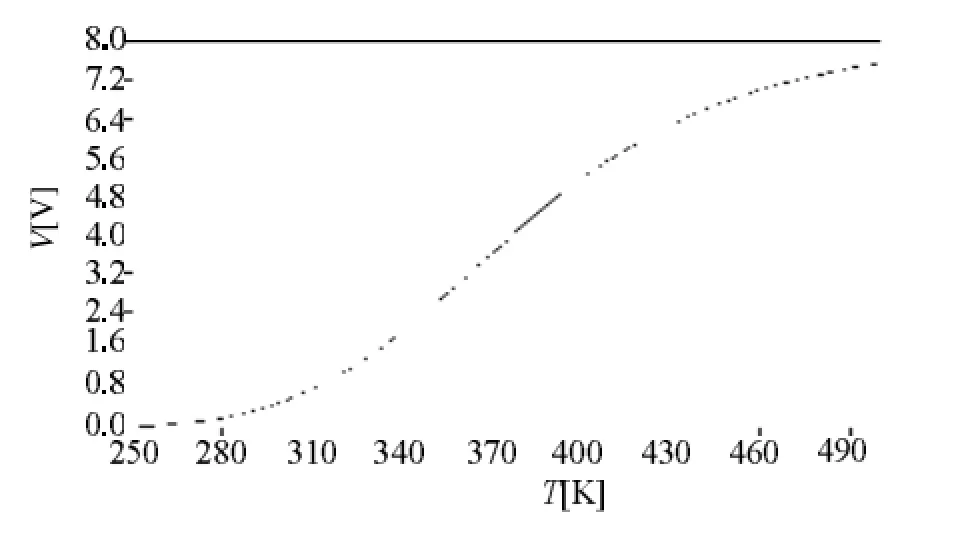
图14　在LTSpice中仿真的桥式网络电路特性曲线

图14中，Y轴表示输出电压（V），X表示温度（K）。与图11比较，可以看出图14的曲线线性度有所提高。图14中线性范围大概在310 K (36.85℃) 到 400 K (126.85℃)之间。 这意味着桥型网络比电阻模式更适合使用在温度较高的应用中。不过，使用桥型网络的热敏电阻依然只有一个相对较窄的线性化区域，而且在实验温度低于250 K和高于500 K后灵敏性也有显著降低。总的来说，使用桥型网络处理后的热敏电阻的线性化性能还是好于使用电阻模式。

4　结论

此文介绍了NTC热敏电阻的线性化方法，也就是热敏电阻的温度补偿方法。对两种具体的方法进行了理论分析和仿真模拟。

第一种方法是让 NTC热敏并联一个普通电阻。这种方法经济简单，在许多商业产品中使用的都是此方法，特别是一些传感器反馈系统中。此文在LTSpice中对此方法进行了仿真模拟，从仿真结果中可以看出热敏电阻经此方法处理后线性度有了显著提高。此方法的弊端是线性区域相对较窄，并且会使热敏电阻的准确性和灵敏性有所降低。

第二种方法是基于惠斯通电桥搭建一个补偿电路。此方法相较于第一种方法性能更好，能提供一个更好的线性度和一个更宽的线性范围。但此电路较为复杂，对于一些集成型和微型的温度测试应用不是太适用。

[1] GE Measurement and Control，“NTC Thermistors,”[Online]. Available: http: //www.ge-mcs. com/ download/ appnotes/ntcnotes.pdf. [Accessed 20 4 2013].

[2] K. K. Rajanish and N. M. Gourish，“Thermistors-In Search of New Applications,Manufacturers Cultivate Advanced NTC Techniques,” Sensor Review，pp. 334-340，22 4 2002.

[3] D. P. Jones，Biomedical Sensors，Momentum Press，2010.

[4] B. C. Baker，“Thermistors in Single Supply Temperature Sensing Circuits,” Microchip，2004.

[5] Maxim Integrated Products，“Using Thermistors in Temperature Tracking Power Supplies,” Maxim Itegrated，2001.

[6] S. B. Stankovic and P. A. Kyriacou，“Comparison of Thermistor Linearization Techniques for Accurate TemperatureMeasurementinPhaseChange Materials,” School of Engineering and Mathematical Sciences，London，2010.

[7] C. Renneberg and T. Lehmann，“Analog Circuits for Thermistor Linearization with Chebyshev-Optimal Linearity Error,” in 18th European Conference on Circuit Theory and Design，Sevilla，2007.

[8] EPCOS，“NTC Thermistors Application Notes,”EPCOs，2009

[9] CE Measurement and Control，''Datasheet: Chip Thermistor in DO-35 Glass Package''，URL: http://physics.syr.edu/courses/PHY351.05Spring/ther mistor-specs.pdf. [Accessed 20 4 2013].

Linearization of the Thermistor Characteristics

Fan Pei，Hu Xu，Yu Jun
(Wuhan Institute of Marine Electric Propulsion，Wuhan 430064，China)

The linearization of a NTC thermistor is presented. Firstly，the theory and the characteristics of the NTC thermistors are discussed. Secondly，the introduction of the varied methods for analogue linearization of thermistors is followed. Then，the two methods: Resistance mode linearization and Bridge network linearization are used to linearize a NTC thermistor. After theory analysis，the circuits based on the two methods are simulated by LTSpice and MTALAB，respectively.

NTC; thermistor; linearization

TP212

A

1003-4862（2015）12-0049-05

2015-09-08

樊霈（1989-），男，助理工程师。研究方向：电气工程及其自动化。