考虑风电场并网的电力系统优化调度研究

邱武强，唐文俊

（海军驻广州广船公司军事代表室，广州 510382）

考虑风电场并网的电力系统优化调度研究

邱武强，唐文俊

（海军驻广州广船公司军事代表室，广州 510382）

本文建立了考虑风电场并网电力系统优化调度模型，目标包括运行风风、燃料成本和污污排放量三个目标，约束条件包括电力电量平衡约束、火电机组有功出力约束、火电机组出力爬坡约束、线路传输容量约束，采用直流潮流计算方法对线路潮流进行计算，采用蒙特卡洛法对模型随机变量进行处理。最后，基于粒子群算法对含风电场的IEEE 30节点标准系统算例进行了仿真建模求解。

电力系统旋转备用优化调度蒙特卡洛

0　引言

随着电网复杂程度的提升、化石能源的短缺以及风能等新能源的不断发展，电力系统优化调度面临的要求和挑战日益增多，国内外对风电场电力系统优化调度问题做了大量研究。其中，确定性建模方法将风电出力预测值的一定百分比作为附加的旋转备用需求，以达到确保系统可靠运行的目的［1］，但易造成旋转备用不足或浪费。模糊建模方法定义隶属度函数，将风电随机性的影响纳入考虑，但难以得到客观调度方案［2］。

针对该现状，本文采用概率建模方法建立了考虑风电场并网电力系统优化调度模型。

1　风电并网系统多目标优化调度模型

1.1模型目标函数

1）系统总燃料成本

在实际系统中的汽轮机组并网运行时，汽轮机进气阀突然开启，会出现 “拔丝现象”，从而在机组的耗量特性曲线上叠加一个脉动效果，产生“阀点效应”。计及阀点效应的系统总燃料成本F［3］：

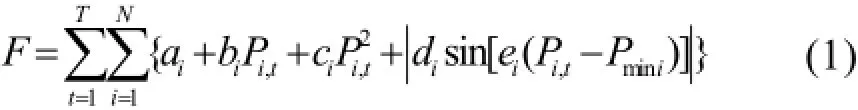
式中：T为调度总时段数；N为常规火电机组总数；Pi，t为机组i在时段t的有功出力；ai、bi、ci、di、ei为机组i燃料成本系数。

2）系统总污污排放

系统火电机组会产生SO2、NOx和CO2等污污气体，其排放量可表示为常规火电机组有功出力的函数［4］。系统总污污排放量E表示为：

式中：αi、βi、γi、ζi、λi为火电机组i的污污气体排放量系数。

3）系统风风系数

风电并网电力系统无法对负荷和风电场出力进行有效控制，故需预留一定旋转备用以应对不可控量的波动。以往研究中，不确定性都仅在模型约束条件中体现，使调度人员无法对优化结果的风风性有客观定量认识。本文定义了系统风风系数来定量衡量调度计划的备用风风程度。风风系数D定义如下：

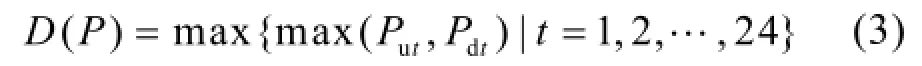
式（3）中：

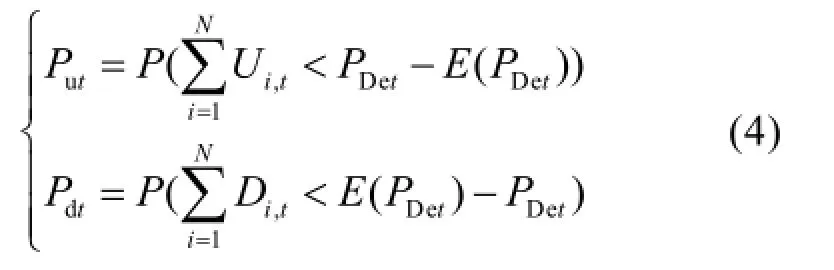
式（4）中：

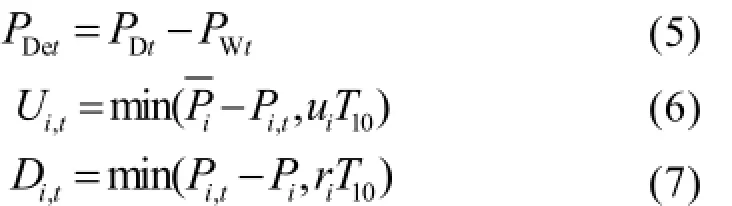
Ui，t、Di，t分别表示常规火电机组i在时刻t可提供的正负旋转备用容量；PDet、PDt、PWt分别表示系统时刻t的净负荷、实际负荷、风电场实际出力；ui、ri分别表示机组i的分钟级上下爬坡速率；和分别表示机组i的出力上下限；T10表示旋转备用响应时间，取值10分钟；E（PDet）表示PDet的期望值。

1.2模型约束条件

1）电力电量平衡约束

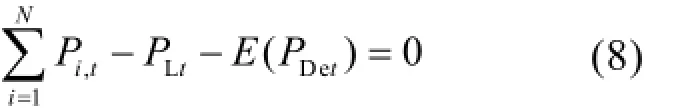
式中：PLt表示系统在时刻t的网损。

2）火电机组有功出力约束

3）火电机组出力爬坡约束

机组有功功率输出变化范围会受到爬坡约束的限制：

4）系统线路传输容量约束

为了保证系统安全运行，还要一定程度兼顾电网的静态安全：

式中：Ll，t表示线路l在t时刻的有功潮流分别表示线路l有功潮流传输上下限。

5）系统风风约束

根据调度人员对风风性的要求，令风风系数小于某一阈值：

1.3基于直流潮流的线路潮流计算

对于有N个节点和L条支路的电力网络的支路（i， j），忽略线路充电电容和变压器支路等等值并联支路后，其有功潮流方程写作：

式中：gij表示支路电导，bij表示支路电纳。

在标幺值下近似认为：Vi=Vj=1，sinθij=θij，cosθij=1，rij=0。采用直流潮流模型对系统有功潮流进行求解［5］，式（13）可简化为：

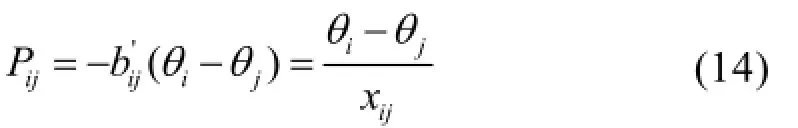
将式（14）写作矩阵形式，有：

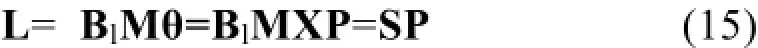
直流潮流模型网损可表示为：

式中：P为N个节点注入有功功率向量；B为N×N阶节点导纳矩阵；θ为N个节点相角向量；X为扩展电抗阵，通过B0求逆后再在参考节点对应行列补0元素得到；L为L条支路有功潮流向量；Bl为L条支路电纳所建立的L×L对角矩阵；M为支路节点关联矩阵；S为支路功率转移分布因子矩阵；R为支路电阻建立的L×L对角矩阵。

1.4 数学模型

考虑风电场并网的电力系统多目标优化调度数学模型表示为：

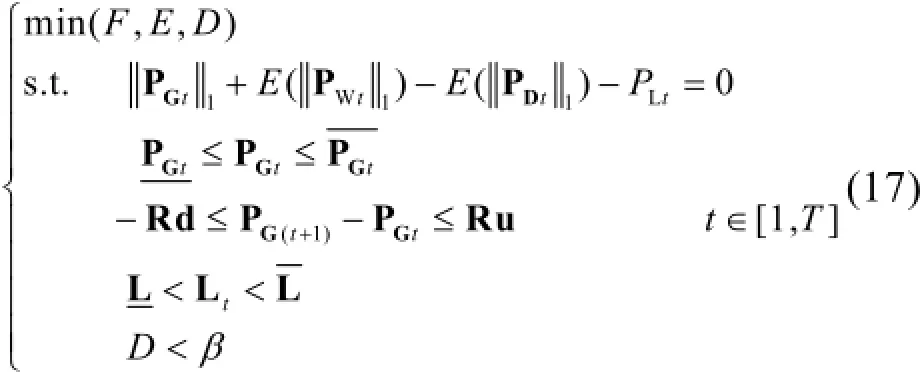
式中：min（F，E，D）表示对多目标模型进行帕累托最小化［6］；PGt、PDt、PWt分别表示t时刻各常规火电机组有功出力、各负荷节点有功负荷、各风电机组有功出力构成的向量

表示t时刻各常规火电机组的有功出力上限和下限构成的向量；Ru和Rd表示各常规火电机组小时爬坡上限和下限构成的向量；表示系统各条支路有功传输上下限构成的向量；Lt表示系统t时刻各条支路有功潮流构成的向量。

2　模型随机变量分析

短期负荷预测误差近似呈正态分布。令时刻t的预测负荷为PDft，负荷预测偏差量为ΔPDt，则：

σDt可由下式求得：

与负荷相比，有着更强的波动性和随机性的风电出力可能从 0至机组装机容量之间进行变化。令时刻t的风电功率预测值为PWft，预测偏差量为ΔPWt，则：σWt可由下式求得：

式中：

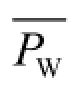
表示风电场总装机容量。

本文采用蒙特卡洛模拟处理模型随机变量。蒙特卡洛模拟，亦即随机模拟，是一种实现随机（或确定）系统抽样试验的技术，其基础是从给定的概率中抽取随机变量［7］。

3　基于粒子群算法的仿真建模求解

粒子群算法是一个群体寻优过程，群体中的个体根据对环境的适应向最优位置迁移。设n维种群中有M个粒子，则第i个粒子的速度和位置更新公式为：

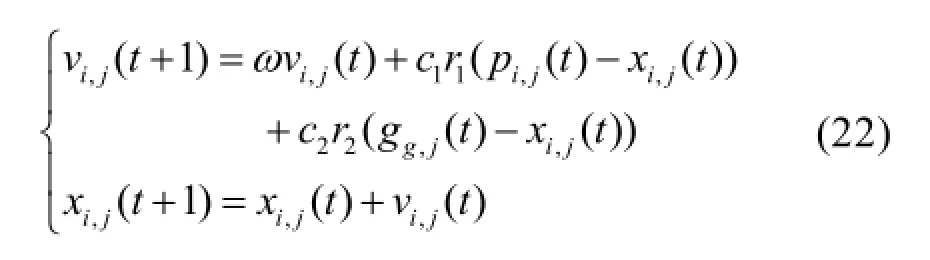
式中，t为进化代数；c1、c2为学习因子；r1、r2为［0，1］区间的随机数；ω为惯性权重；pi，j和 gi，j表示第i个粒子的个体最优解和全局最优解。

算例采用风电场并网的IEEE 30节点标准系统，含有6台常规火电机组和1个风电场，接线图如图 1所示。风电场装机容量为 150MW，从节点22并入系统。系统线路参数、线路传输功率极限以及各节点负荷占总负荷的比例参见文献［5］。假设各节点负荷占总负荷的比例在各时刻保持不变。系统第13条支路（即节点12-13之间的支路）的传输极限由标准系统中标幺值下的0.65下调为0.16。

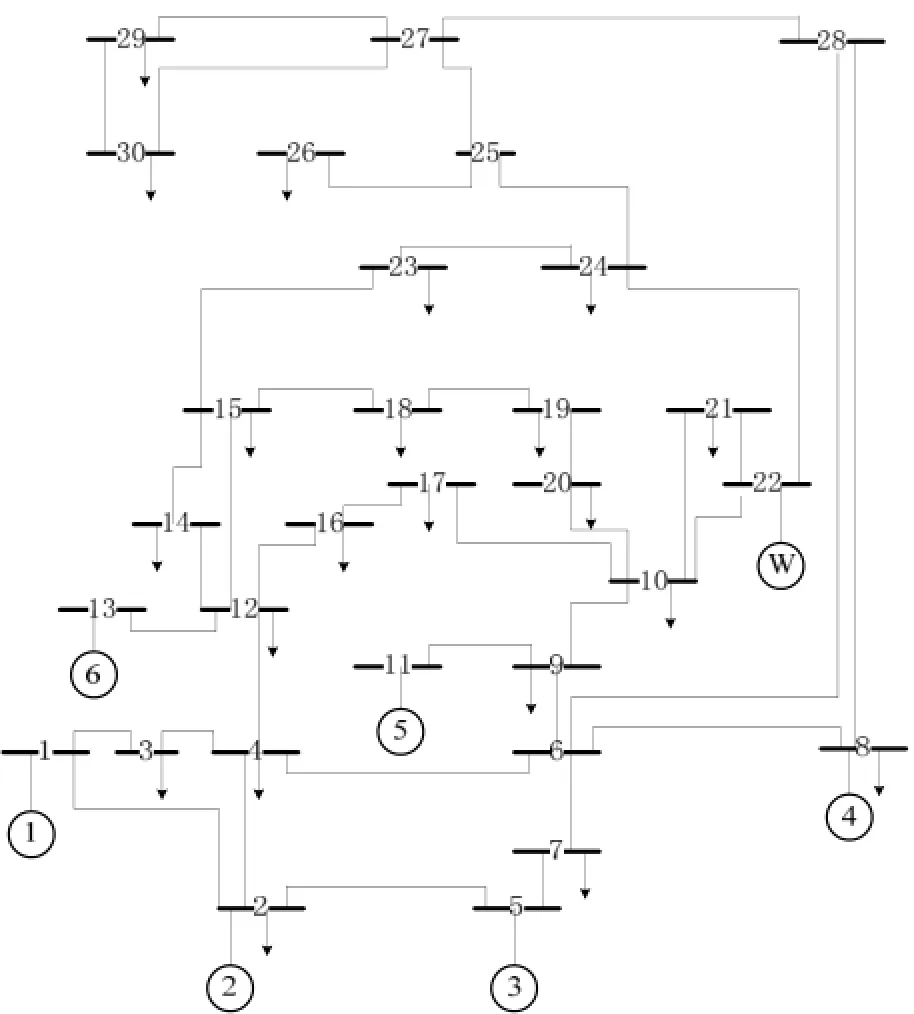
图1　IEEE 30节点系统接线图

采用Matlab R2012a进行仿真试验的建模与求解。最终方案集在目标空间及“燃料成本-污污排放”目标平面中的分布如图2所示，将其划分为4个风风等级。最小燃料成本方案已在图2中标出，其燃料成本、污污排放量及风风系数分别为1.6414×104$、5.2864 ton和0.0488，所有机组各时段均满足出力上下限约束、出力爬坡约束与功率平衡约束，且功率平衡约束违背值在 1×10-6MW内。

4　总结

本文建立了考虑风电场并网的电力系统优化调度模型，目标函数包括计及阀点效应的总燃料成本、总污污排放、系统风风系数，约束条件包括电力电量平衡约束、火电机组有功出力约束、火电机组出力爬坡约束、线路传输容量约束，采用直流潮流计算方法对系统线路潮流进行计算，采用蒙特卡洛法对模型中的随机变量进行处理，采用粒子群算法对模型进行了求解，优化结果以方案集呈现，可使调度人员在不同工况要求下进行选择，具有较高的工程应用价值。

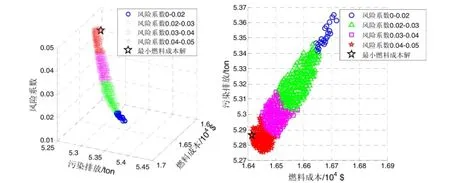
图2　求解最终方案集

［1］ 周玮， 彭昱， 孙辉， 等. 含风电场的电力系统动态经济调度［J］. 中国电机工程学报， 2009， 29（25）: 13-18.

［2］ 陈海焱， 陈金富， 段献忠. 含风电场电力系统经济调度的模糊建模及优化算法［J］. 电力系统自动化，2006， 30（2）: 22-26.

［3］ Allen J W， Bruce F W. Power generation， operation，and control［M］. John Wiley & Sons， New York， 1984. ［4］ Wu L H， Wang Y N， Yuan X F， et al. Environmental/economic power dispatch problem usingmulti-objectivedifferentialevolution algorithm［J］. Electric Power Systems Research， 2010，38（8）: 121-124.

［5］ 张伯明，陈寿孙. 高等电力网络分析［M］.北京:清华大学出版社，1996.

［6］ Eckart Z， Lothar T. An evolutionary algorithm for multiobjective optimization: The strength Pareto Approach，TIK-ReportNo.43［R］.Computer Engineering and Network Lab，1998.

［7］ 孙元章， 吴俊， 李国杰， 等. 基于风速预测和随机规划的含风电场电力系统动态经济调度［J］. 中国电机工程学报， 2009， 29（4）: 41-47.

Multi-objective Dispatch in Wind Power Integrated System

Qiu Wuqiang， Tang Wenjun （Naval Representatives Office in Guangzhou Shipyard International Company Limited， Guangzhou 518302）

A modeling for multi-objective optimized dispatch in wind power integrated system is established，whose goal is to control operational risks， fuel costs and pollution emission. The constraint conditions include real power operation limits， real power balance constraints， generating unit ramp rate limits and line capacity constraint. DC power flow method is used to calculate the transmission line flow， Monte-Carlo method is introduced to deal with the random variables. At last， the model is solved using PSO.

power System； spinning reserve； optimized dispatch； monte-carlo

TM731

A

1003-4862（2015）12-0065-04

2015-10-08

邱武强（1973-），男，工程师。研究方向：舰船电气工程。