相位复原算法比较分析

王金洋，曹继华

（天津职业技术师范大学电子工程学院，天津300222）

相位复原算法比较分析

王金洋，曹继华

（天津职业技术师范大学电子工程学院，天津300222）

相位复原算法分为迭代法和强度传输方程法，本文对迭代法中的GS算法和HIO算法以及强度传输方程法进行了分析对比。针对3种相位复原算法基本原理，分别通过实验比较了3种算法在初始值为0和随机数情况下的收敛速度和复原精度，证明GS算法和强度传输方程法在初始值为0时有更好的复原效果，HIO算法在初始值为随机数时有更好的复原效果。通过3种相位复原算法在初始值为随机数的实验比较，证明HIO算法比GS算法和强度传输方程法有更好的复原效果和复原精度。

GS算法；HIO算法；相位复原；强度传输方程法

研究表明，相位是波的一种内在特性，波的振幅中包括1/4左右的信息，大约3/4的信息则在相位中。相位信息中通常携带关于物体结构的重要信息，但目前的探测器只能接收到物体在某种射线照射下的衍射光数据，因而会导致物体相位信息丢失。这些丢失的相位信息在一些物理应用中具有十分重要的作用，因此相位复原成为国际研究工作者关注的重点。研究人员最初的想法是利用全息技术随幅度信息的测量捕捉相位信息，但装置的实现很困难，所以仅使用测量的强度信息获得相位信息引起了更多的关注。研究人员提出了许多方案，并不断进行改进。1972年，Gerehberg和Saxton［1］提出了GS相位复原算法，该算法是第一种被广泛接受的相位复原算法。GS相位复原算法奠定了数值相位复原衍射迭代的基本模式，成为相位复原数值领域的经典算法。其基本思路是将波前交替在物面及成像面上来回传播，并分别施加其振幅所满足的约束，逐步收敛于实际复振幅。然而，GS算法在实际应用中存在一些缺点，如迭代次数过多、收敛性不好、依赖双强度测量等，限制了其在实际中的应用。针对GS算法存在的不足，研究人员提出了改进方案。其中，Fienup［2-4］提出的混合输入输出算法（hybrid input-output，HIO），在迭代过程中引入了支撑域约束，使HIO算法具有较好的收敛性能，在针对实值非负物体的相位复原中有广泛应用。本文主要分析了GS算法、HIO算法和强度传输方程法［5-6］在求解相位复原问题中的基本原理和步骤，通过实验分析初始相位对复原结果的影响，比较3种相位复原算法最终的复原效果。

1　GS相位复原算法

1.1GS相位复原算法的基本原理

GS算法可以描述为gk表示第k次迭代时，用各个gm，k对f的联合估计，即

GS算法步骤如下：

（a）初始化k=0，θm，k为初始相位估计。

重复步骤（b）～（f），直到退出条件。退出条件可以是迭代次数的限制，也可以是式（7）中的目标函数达到某一特定值。

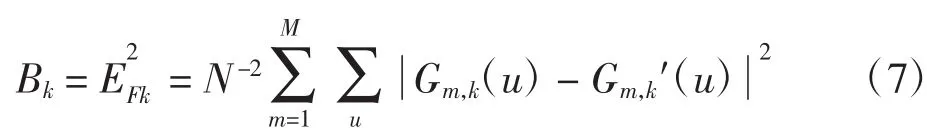
根据GS相位复原算法的基本原理可以得到GS相位复原算法流程图，如图1所示。

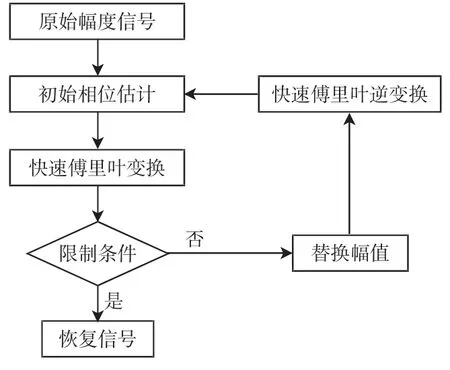
图1　GS算法流程图

1.2GS算法实验

实验中选取了不同的初始相位，算法初始相位为0迭代产生的图像如图2所示，算法初始相位为随机数迭代产生的图像如图3所示。

图2　GS算法初始相位为0迭代产生的图像

图3　GS算法初始相位为随机数迭代产生的图像

从图2和图3分别对应的6个分图可以看出GS算法在初始相位为0和随机数时的变化过程。GS算法不同初始相位的比较如图4所示。通过图4可以看出，GS算法在初始相位为随机数时有更好精确度，并且收敛速度更快。

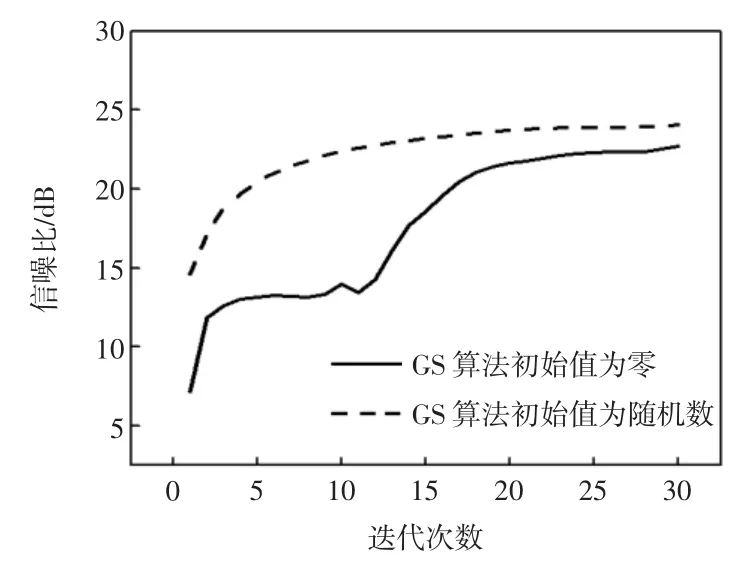
图4　GS算法不同初始相位的比较

2　HIO算法

2.1HIO算法的基本原理与流程

混合输入输出算法（HIO）不同于GS算法，它仅在目标域内进行计算。HIO算法的3个步骤与GS算法相似，即：①g（x）进行傅里叶变换；②满足傅里叶变换域内投影的条件；③进行傅里叶逆变换得g′（x）。由于混合输入输出算法在GS算法的基础上加入了一个投影的过程，使输入的g（x）不需满足对象域的限制并且输出始终能满足该傅里叶域约束，这样可以更方便地产生下一个输入，使算法快速收敛并得出结果。HIO算法的迭代过程可概括如下：

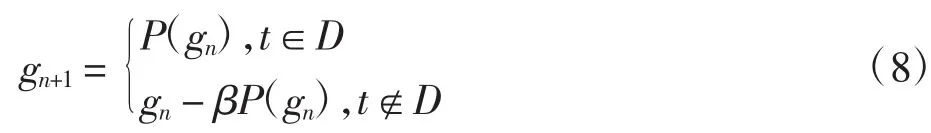
式中：gn、gn+1分别是这一次与下一次迭代图像。投影算符P（gn）可以作如下描述：先对gn取傅里叶变换，变换后的结果设为m，保持相位不变并将振幅修改为测量值；然后求取傅里叶逆变换，抑制系数β＜1，一般可取0.9。算法从初始值开始，经不断的交替投影迭代。终止条件可以设定为迭代次数的限制，也可以达到指定的精度。

HIO算法的流程与GS算法相似，不同之处在于GS算法的幅值替换时加入了一个投影过程，限制了幅度的变化方向，使其仅在目标域内进行计算，HIO算法流程如图5所示。

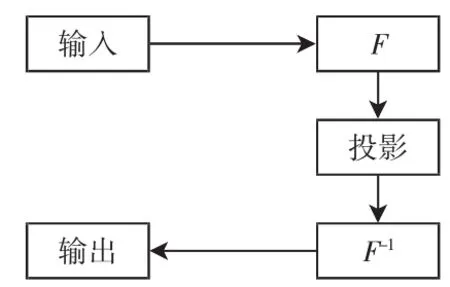
图5　HIO算法流程图

2.2HIO算法实验

实验中选取了不同的初始相位，算法初始相位为0迭代产生的图像如图6所示，算法初始相位为随机数迭代产生的图像如图7所示。

图6　HIO算法初始相位为0迭代产生的图像

通过图6和图7分别对应的6个分图可看出HIO算法在初始相位为0和随机数时的变化过程。HIO算法不同初始相位的比较图如图8所示，通过图8可以看出，HIO算法在初始相位为0时具有更好的精确度，并且收敛速度更快。

图7　HIO算法初始相位为随机数迭代产生的图像

图8　HIO算法不同初始相位的比较

3　强度传输方程法解相位复原问题

3.1强度传输方程法的基本原理

解决相位复原问题，还可以利用强度传输方程法列出一个线性矩阵方程组并求解。假设使用y和测量矩阵A=［a1，a2，…，am］，A∈Cn×m为测量矩阵，ai是A的第i列；y为测量的幅度值，矩阵方程为：

假设x*为复原后的图像，即带有相位的图像，则相位复原问题转化为利用测量的幅度值y和测量矩阵A复原x*的问题。假设C*为ATx真实相位，求解的问题就简化为解决一个线性系统的等式：

由于不知道C*，复原x*的变为求解矩阵方程：

求解矩阵方程采用牛顿最速方向下降法，即交替更新x和C*，最终求解出符合精度要求的x*。

3.2强度传输方程法实验

实验中初始相位的取值为0或随机数，选取为离散余弦变换（DCT）。方程法初始相位为0迭代产生的图像如图9所示，初始相位为随机数的方程法迭代产生的图像如图10所示。

图9　强度传输方程法初始相位为0迭代产生的图像

图10　强度传输方程法初始相位为随机数的迭代产生的图像

通过图9和图10可以看出强度传输方程法在初始相位为0和随机数时的变化过程。强度传输方程法不同初始相位的比较如图11所示。通过图11的比较可以看出，强度传输方程法在初始相位为0时有更好的精确度，并且收敛速度更快。

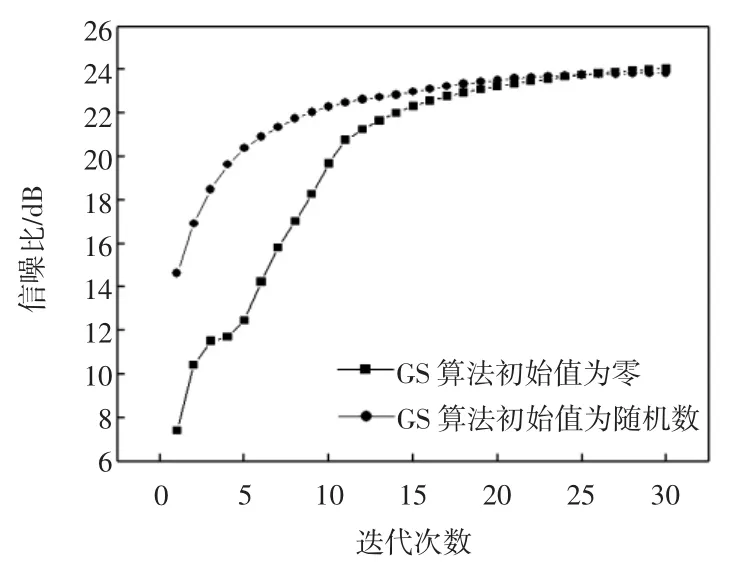
图11　强度传输方程法不同初始相位的比较

3.3相位复原算法的比较实验

为比较GS算法、HIO算法和强度传输方程法的相位复原效果，在实验中初始相位均选取为随机数，迭代次数为1 000次。3种算法的比较结果如图12所示。通过图12可以明显看出，HIO算法有更快的收敛速度及收敛精度，强度传输方程法的结果与GS算法的结果接近。

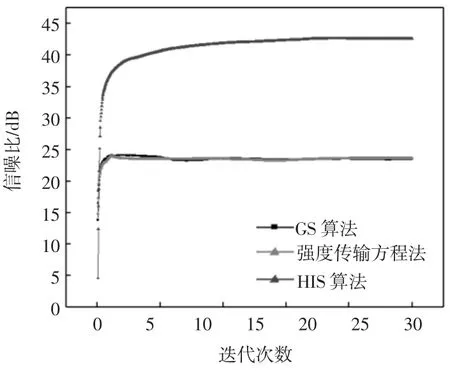
图12　GS算法、HIO算法和强度传输方程法的比较

4　结束语

本文对GS算法、HIO算法和强度传输方程法这3种相位复原算法进行了对比分析。通过对3种算法在初始值为0和随机数时的收敛速度和复原精度进行比较，得出了GS算法和强度传输方程法在初始值为0时有具更好复原效果，HIO算法在初始值为随机数时具有更好复原效果。同时比较了3种相位复原算法在初始值为随机数的复原效果，对比结果表明：HIO算法优于GS算法和强度传输方程法。

［1］GERCHBERG R W，SAXTON W O.A practical algorithm for the determination of phase from image and diffraction plane pictures［J］.Optik，1972，35（2）：237-250.

［2］FIENUP J R.Phase-retrieval algorithms for a complicated optical system［J］.Applied Optics，1993，32（10）：1737-1746.

［3］FIENUP J R.Phase retrieval algorithms：A comparison［J］. Applied Optics，1982，21（15）：2758-2769.

［4］FIENUP J R，WACKERMAN C.Phase retrieval stagnation problems and solutions［J］.OpticalSocietyofAmerica，1986，3（11）：1879-1907.

［5］PRANEETH N，PRATEEK J，SUJAY S.Phase retrieval using alternating minimization［C］//27th Annual Conference on Neural Information Processing Systems 2013.Nevada：Neural Information Processing Systems，2013：2796-2801.

［6］MUKHERJEE S，SEELAMANTULA C.An iterative algorithm for phase retrieval with sparsity constraints：Application to frequency domain optical coherence tomography［C］// Acoustic，Speech and Signal Process（ICASSP），2012 IEEE International Conference on IEEE.Kyoto：IEEE，2012：553-556.

Comparison of phase retrieval algorithm

WANG Jin-yang，CAO Ji-hua
（School of Electronic Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

The phase retrieval algorithm is divided into the iterative method and the intensity transmission equation method. This paper introduces GS algorithm and HIO algorithm in the iterative method and the intensity transmission equation method.For the basic principles of the three phases retrieval algorithm，the convergence speed and accuracy of the three algorithms are compared through experiments in the case of an initial recovery value of zero or random matrix.It is proved that GS algorithm and intensity transmission equation method have a better recovery effect when the zero matrix，HIO algorithm has a better effect in the initial recovery value when the random matrix.The comparison of three phase retrieval algorithm，proved that HIO algorithm has better effect recovery and retrieval precision than GS algorithm and intensity transmission equation.

GS algoricthm；HIO algorithm；phase retrieval algorithm；intensity transmission equation

TP301.6

A

2095－0926（2015）04－0036－04

2015-09-11

国家自然科学基金资助项目（61271412）.

王金洋（1990—），男，硕士研究生；曹继华（1964—），男，教授，博士，研究方向为盲信号处理、压缩感知.