受迫振动实验数据处理方案的探讨
常 成,章 羽
(东南大学,江苏南京 211189)
受迫振动实验数据处理方案的探讨
常 成,章 羽
(东南大学,江苏南京 211189)
修改了现行教学用网络数据处理系统中的幅频特性描述和求解阻尼系数的方法,采用非线性拟合,不仅能直观描述蜗卷弹簧性能的差异,同时可以从拟合曲线中方便地求解实验的阻尼系数。这是一种实时的数据处理方式,研究结果可成为仪器生产单位数据处理软件的开发方案,为实验室教师机上显示各组仪器的特性曲线和求解阻尼系数提供了一种更直接的方式。
受迫振动;幅频特性;非线性拟合;阻尼系数
1 问题的引出和思考
在大学基础物理实验“受迫振动的研究”中注意到,由于实验仪器的各异性以及制造工艺和材料性能的影响,蜗卷弹簧的弹性系数k值随扭转角度的改变而略有变化[1-5],造成利用幅频特性曲线求阻尼系数δ时,有的幅频特性曲线产生较大变形(如图1、图2),而有的则变形较小。教材中建议的求解阻尼系数的两种方案和教学用网络数据处理系统中求解阻尼系数的方案都没有直接从每个仪器的实测幅频特性曲线中去求解,究其原因应该是各个仪器蜗卷弹簧差异性问题,给实时拟合各仪器的幅频特性曲线并求解阻尼系数带来困难以致现有的实验室教师机上没有从拟合曲线中求解阻尼系数。针对这些问题,本文选取了较为典型的3种蜗卷弹簧情况进行了探究,提出一种实时的数据处理方案。

图1 幅频特性曲线
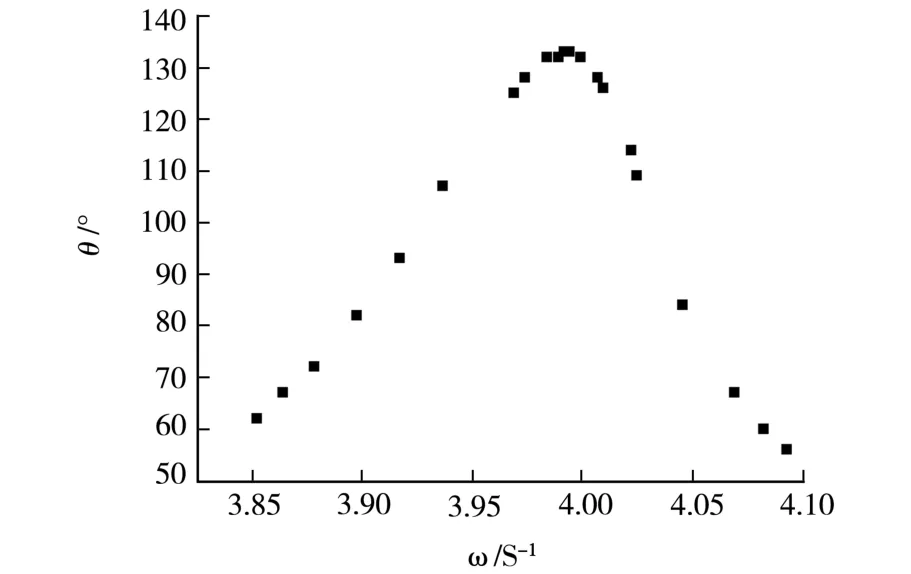
图2 幅频特性曲线
2 实验方案的设计和探讨
由于实物弹簧的性能导致系统的固有频率ω0并非恒为定值,使得实验室中几十台仪器的幅频特性曲线是有程度不同的诸如图1、图2中的变形。为了观察系统的固有频率ω0在小范围内变化所带来的影响,由受迫振动公式(1)
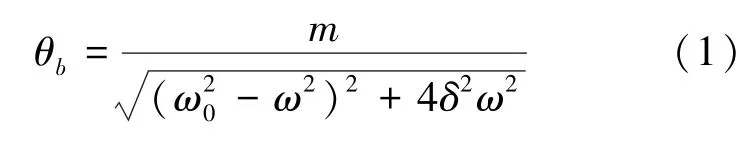
令ω0取峰值,a=m,b=4δ2并设其为待定系数,代入式(1)得:
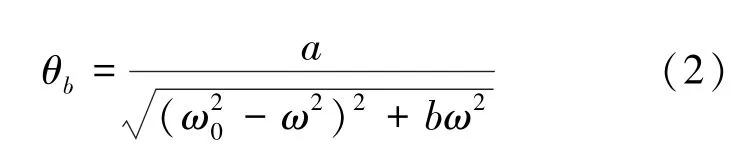
图3的拟合曲线较原始数据点偏离较大,特别是在峰值处,当ω0接近ω时,θb增加很快,变化幅度大,此时再让ω0只是简单取峰值时的值,拟合图像就会出现较大偏差,由此可见,系统的固有频率ω0在小范围内变化在拟合图像上带来的影响较大。
由于系统的固有频率ω0在小范围内的变化对于幅频特性曲线拟合的影响不可忽略,为了更好地观察系统的固有频率ω0的波动情况,从而对幅频特性曲线进行更精确的拟合,我们认为ω0与ω存在一定的关系,并由此描绘出两者之间的关系图像(如图4、5、6)。对比之前的幅频特性曲线可以发现,正是由于固有频率不同的波动情况,从而导致了幅频特性曲线的波动不同。
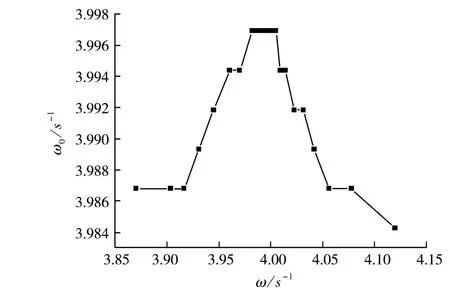
图4 仪器Ⅰ的ω0-ω图像
通过尝试可以发现,ω0与ω的图像大致符合六元五次函数的图像即:
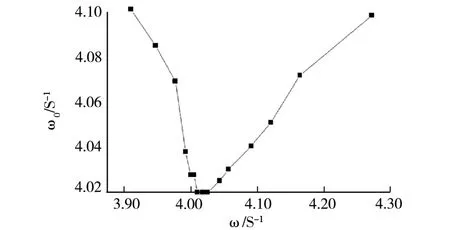
图5 仪器Ⅱ的ω0-ω图像
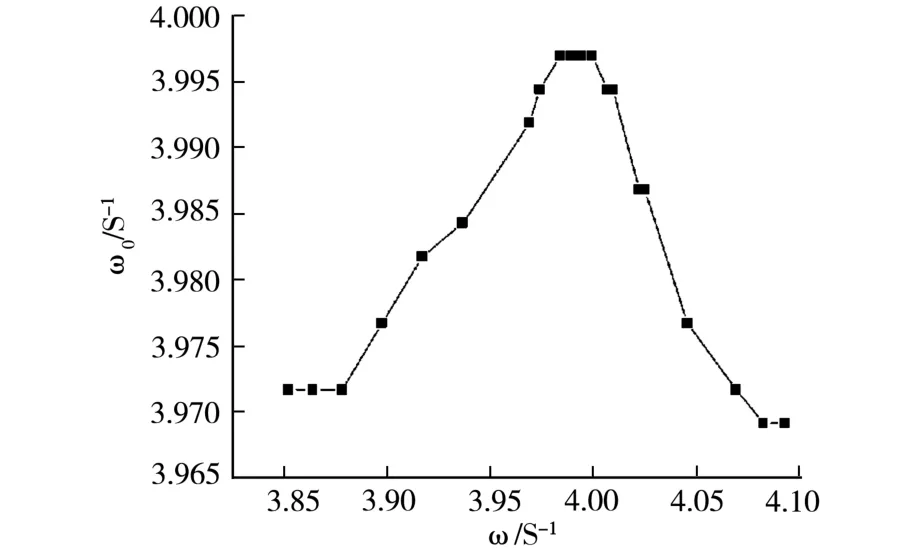
图6 仪器Ⅲ的ω0-ω图像
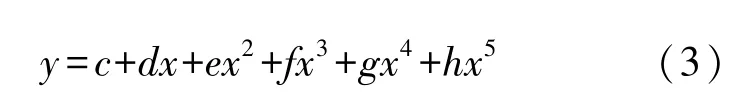
令ω0为y,ω为x,根据最小二乘法原理,容易得到参数c、d、e、f、g、h的值。利用Origin软件[2]得到ω0-ω的拟合图像,从拟合参数的结果可以得到ω0与ω存在的函数关系。
将得到的ω0与ω的函数关系式代入式(1)并令a=m,b=4δ2并设其为待定系数得式(4):

令θb为y,ω为x,根据最小二乘法原理,容易得到a、b的值。
利用Origin软件[2]得到幅频特性曲线(如图7、8、9),从拟合参数的结果可得b的值。

图7 仪器Ⅰ的拟合图像

图8 仪器Ⅱ的拟合图像

图9 仪器Ⅲ的拟合图像
观察图7、8、9,可以发现这三种典型的幅频特性曲线均取得了较为理想的拟合效果,从而得到了一种实时的数据处理方案。
3 实验的结果与结论
通过对受迫振动实验的数据处理方案的探究,基于是否考虑系统的固有频率在小范围内变化的理论分析,结合实验数据的非线性拟合,与一般的以ω/ω0为横坐标不同,直接以ω为横坐标,θb为纵坐标,根据最小二乘法原理,得出各组仪器的拟合曲线,从而验证了系统的固有频率对幅频特性曲线的影响较大。研究结果可以为仪器生产单位提供数据处理的软件开发方案,为实验室教师机上显示各组仪器的特性曲线和求解阻尼系数提供了一种可行方式。
[1] 钱锋,潘人培.大学物理实验[M].北京:高等教育出版社,2005:87-94.
[2] 方安平,叶卫平.Origin 8.0实用指南[M].北京:机械工业出版社,2009:170-173,189-192.
[3] 陈铭南.受迫振动实验的计算机实时测量[J].大学物理实验,1997,10(l):57-59.
[4] 曾明荣..Origin在物理化学实验数据处理中的应用[J].高校实验室工作研究,2007(02).[5] 郎江,张锐波.受追振动实验中几个问题的探论[J].大学物理实验,2013,3:102-105.
The Analysis of Data-processing Method for Forced Vibration Experiment
CHANG Cheng,ZHANG Yu
(Southeast University,Jiangsu Nanjing 211189)
Based on the data processing system used in teaching,we modify the existing method for the description of amplitude-frequency characteristics and the solution of the damping coefficient.We employ a nonlinear fitting technique,which not only makes a visual display of the differences between scroll spring performances,but also provides an easy way to solve the experimental damping coefficient via fitting curves.This is a kind of real-time data processing,and its mechanism can be applied to the development of data processing software for instrument manufacturers.Thus a more direct way of demonstrating the characteristic curves and solving the damping coefficient problem on a teacher machine is available.
forced vibration;amplitude-frequency characteristics;nonlinear fitting;damping coefficient
O4-39
A
10.14139/j.cnki.cn22-1228.2015.02.034
1007-2934(2015)02-0118-03
2014-11-13

