基于Stochastic Kriging的柔性机翼稳健性优化设计

刘艳，白俊强，华俊，2，刘南，王波

1.西北工业大学航空学院，陕西西安 710072；2.中国航空研究院，北京 100012 3.中国航天空气动力技术研究院，北京 100074

基于Stochastic Kriging的柔性机翼稳健性优化设计

刘艳1，白俊强1，华俊1，2，刘南1，王波3

1.西北工业大学航空学院，陕西西安 710072；2.中国航空研究院，北京 100012 3.中国航天空气动力技术研究院，北京 100074

采用随机代理模型方法对柔性机翼气动外形进行稳健性优化设计。相比确定性优化设计，稳健性设计能够考虑设计变量和参数的扰动，保持设计结果在不确定性影响下的性能稳定。采用高精度的气动/结构耦合求解器（耦合Navier-Stokes方程和结构静力学方程）分析柔性机翼的变形情况和气动效率。为了提高优化效率，建立随机Kriging（Stochastic Kriging，SK）代理模型，将确定性的Kriging代理模型发展到随机空间，通过有限次输入得到数据的固有不确定性。对柔性M6机翼的气动外形进行稳健性优化设计，结果表明：相比确定性代理模型的稳健性优化结果，应用随机代理模型的优化结果的设计点阻力系数减小2.8 counts，在可变马赫数范围内阻力系数均值减小3.2 counts，优化结果具有较高的设计点气动效率和阻力发散特性，并且优化后构型的翼根弯矩有明显减小，体现随机代理模型在稳健性优化设计系统中的优势，同时也说明建立的SK代理模型具有较高的预测精度。

柔性机翼；稳健性优化；静气动弹性力学；随机Kriging代理模型；Navier-Stokes方程

目前工程中常用的优化设计方法是确定性优化设计，但该方法中设计变量、目标函数和约束函数均为确定性问题，因此不能够反应工程设计、产品制造以及服役环境对设计结果的影响，其中客观存在大量不确定性因素会对设计方案产生影响，而传统优化设计的最优解对于这些不确定性因素非常敏感［1-4］。与传统的确定性优化［5］相比，稳健性优化［6-7］的一个显著特点就是在优化过程中考虑不确定性因素的存在，减小设计目标对不确定性因素的灵敏度，保持设计结果在不确定性影响下性能稳定。稳健性设计的求解方法可以分为确定性方法和随机化方法两类。确定性方法［8］是将不确定性问题通过一定的分析转化为确定性问题，然后利用相关优化算法求解。而通过直接优化扰动量和约束的方法来处理不确定性问题，因此也有时被称为数值优化方法。随机化方法［9-10］通常都是基于直接搜索法开展的研究，不需要显式的一阶或二阶导数，而只需得到下一个位置处的目标函数响应，有效减少了对问题的依赖性。

由于问题规模爆炸式增加，考虑不确定性的稳健性设计计算量很大。为了提高效率，可以将随机化方法与各种代理模型相结合以处理稳健性设计问题。主要是根据一定数量的离散样本数据，通过构造响应的代理模型进行目标特性分析，在保证一定分析精度的基础上大幅缩减计算量，进而加快整个设计系统的效率。这种方法由于相比传统的蒙特卡罗模拟法（Monte Carlo Simulation，MCS）计算量小，可以得到可靠的低阶矩信息等优点，在不确定性领域得到了众多关注。

综上，本文针对柔性机翼在飞行状态不确定性情况，以应用较多的Kriging代理模型为原型建立随机Kriging（Stochastic Kriging，SK）代理模型［11］，构建基础问题，进行统计学推导以及确立相关参数求解方案，得到可靠的估计均值和方差，并通过基础算例验证这一方法在不确定性问题中较强的实用性。通过与基于确定性Kriging（deterministic Kriging，DK）代理模型的稳健性优化结果进行研究对比，验证随机代理模型在稳健性优化设计中的优势。

1　理论基础

1.1气动/结构耦合理论基础

由于要研究考虑飞行状态不确定性影响的柔性机翼设计，需要机翼的静弹性分析方法能够捕捉不同飞行状态下对流场造成的影响。因此建立耦合雷诺平均Navier-Stokes（RANS）方程和结构静力学方程的高精度静气动弹性分析方法。气动模型与结构模型之间载荷传递、弹性变形插值采用RBF插值方法进行，参考文献［11-12］中有详细介绍，此处仅给出静气弹分析流程如图1所示，图中CFD求解器为求解RANS方程，CSD求解器采用柔度影响系数矩阵方法，收敛条件为两次弹性变形差小于给定误差值，动网格采用四元数方法，载荷传递与位移插值均采用径向基函数插值方法。

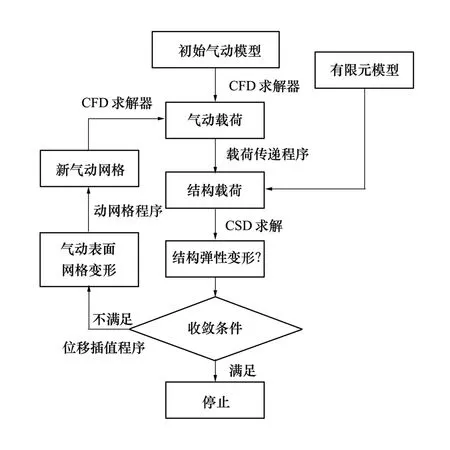
图1　静气弹分析流程图

1.2有限样本的Stochastic Kriging建模

考虑不确定性的重复样本点的情况下，将DK代理模型从确定性空间转化到随机空间中去［10］。为了解决包含各处非均等的不确定性和有限采样点的问题，对空间中的随机样本将通过如下形式表示：

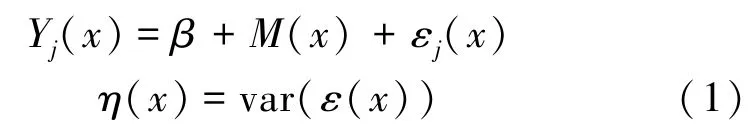
式中，ε（x）被定义为固有不确定性，用来表示扰动项，并被假设为正态分布，εj（x）是固有不确定性的一个实现，表示的是在x处重复样本的扰动，并且被假设为与其他重复样本的固有和非固有不确定性M（x）之间相互独立，η（x）代表的是固有不确定性的方差。这里的输入变量为若干组（xi，Yj（xi），Ni；i =1，2，…，n），其中Ni表示在位置xi处的重复样本的个数，这里的Ni是有限值，各个位置处样本的均值可以相应的表示为

此方法也可采用最优线性估计的形式进行预测，以得到未知位置的均值：

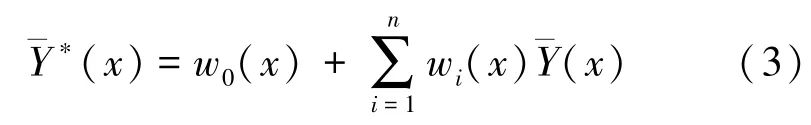
式中，wi（t）表示的是赋予各已知位置均值的权值量，也就是通过已知均值的权重来估计未采样位置处的均值。对于不确定性的Stochastic Kriging模型［10］均方差的构建形式可表示为

在对均方差的构建中，很明显，重复样本的固有不确定性信息被考虑进模型的构建过程中，以表示假设的真值和估计的形式。通过对公式（4）进行展开：

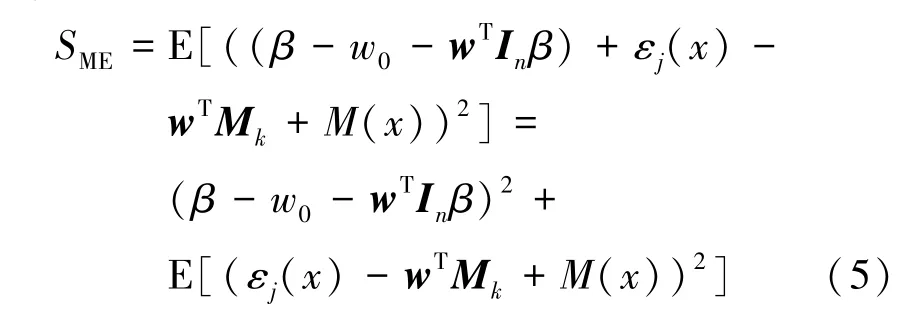
显然，公式（5）中平方和展开的最后一项为零。根据上述独立性假设，公式（5）即可写为

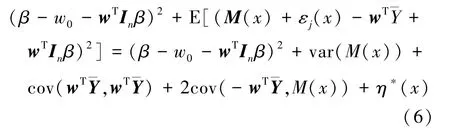
对公式（6）的推导中，比较有代表性的一项可以展开为

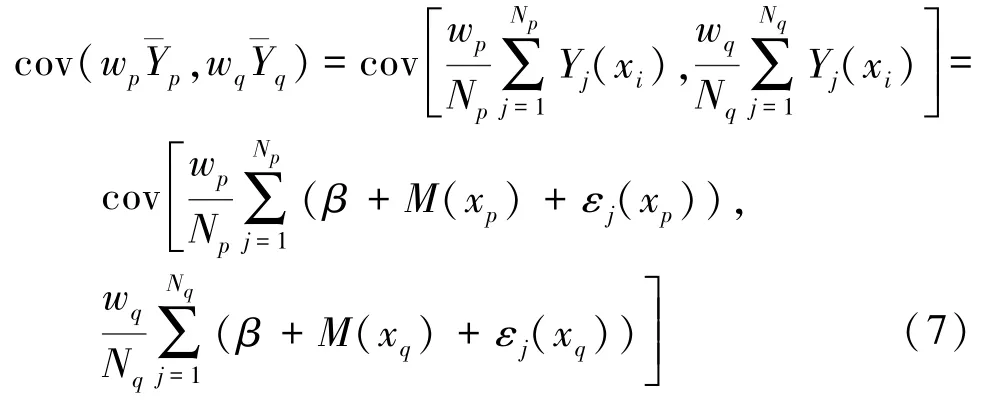
式中，p、q表示的是输入变量的某一位置，1≤p、q≤n。而后利用各重复样本之间相互独立的假设，公式（7）可以展开为

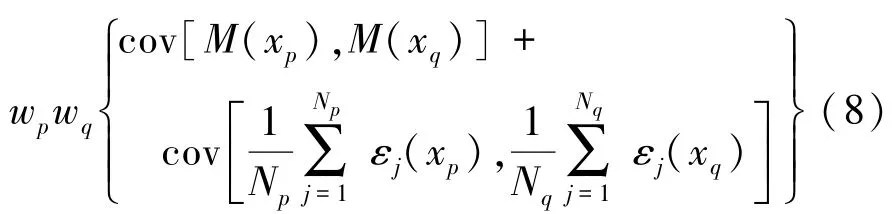
为了简化公式中的符号，基于二阶平稳假设［14］的假设，这里先将（8）式简写为如下的形式

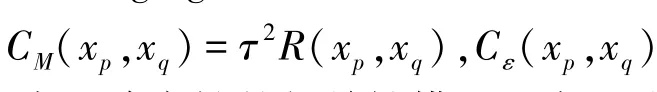
2　基于稳健性设计的柔性机翼设计方法

建立的SK代理模型通过对基础问题的构建、统计学推导以及相关参数求解方案的确立，得到了可靠的估计均值和方差，下面通过算例验证了这一方法在不确定性问题中较强的适用性。柔性机翼稳健性优化设计流程如图2所示。

图2　稳健性优化设计流程图

3　算例分析

本节用设计实例论述SK代理模型的可行性和鲁棒性。以M6机翼为初始构型，设计点状态为：Ma =0.84，Cl=0.271 54，Re=1.172×107，考虑来流马赫数不确定性变化范围Ma∈［0.82，0.83，0.84，0.85，0.86］。3.1节采用基于DK代理模型进行稳健性优化得到优化解。在3.2节应用SK代理模型进行柔性机翼的稳健性设计得到优化解。3.3节对3.1、3.2节的最优结果进行对比，并对结果进行分析。所有优化设计在满足机翼体积不减小的约束条件下进行。

采用改进的FFD参数化方法［14］，该方法克服了原始FFD方法的设计变量相关性强的缺点，适用于精细化外形参数化，FFD控制框及控制点如图3所示，共有3个控制截面，每个剖面有12个控制点控制z坐标，共36个控制点。再加外侧2个剖面的扭转角以及机翼后掠角，因此共有39个设计变量（xi，i=1，2，…，39）。设计变量范围见表1，表中ID代表设计变量序号，lb代表设计变量变化的下限，ub代表设计变量变化的上限。

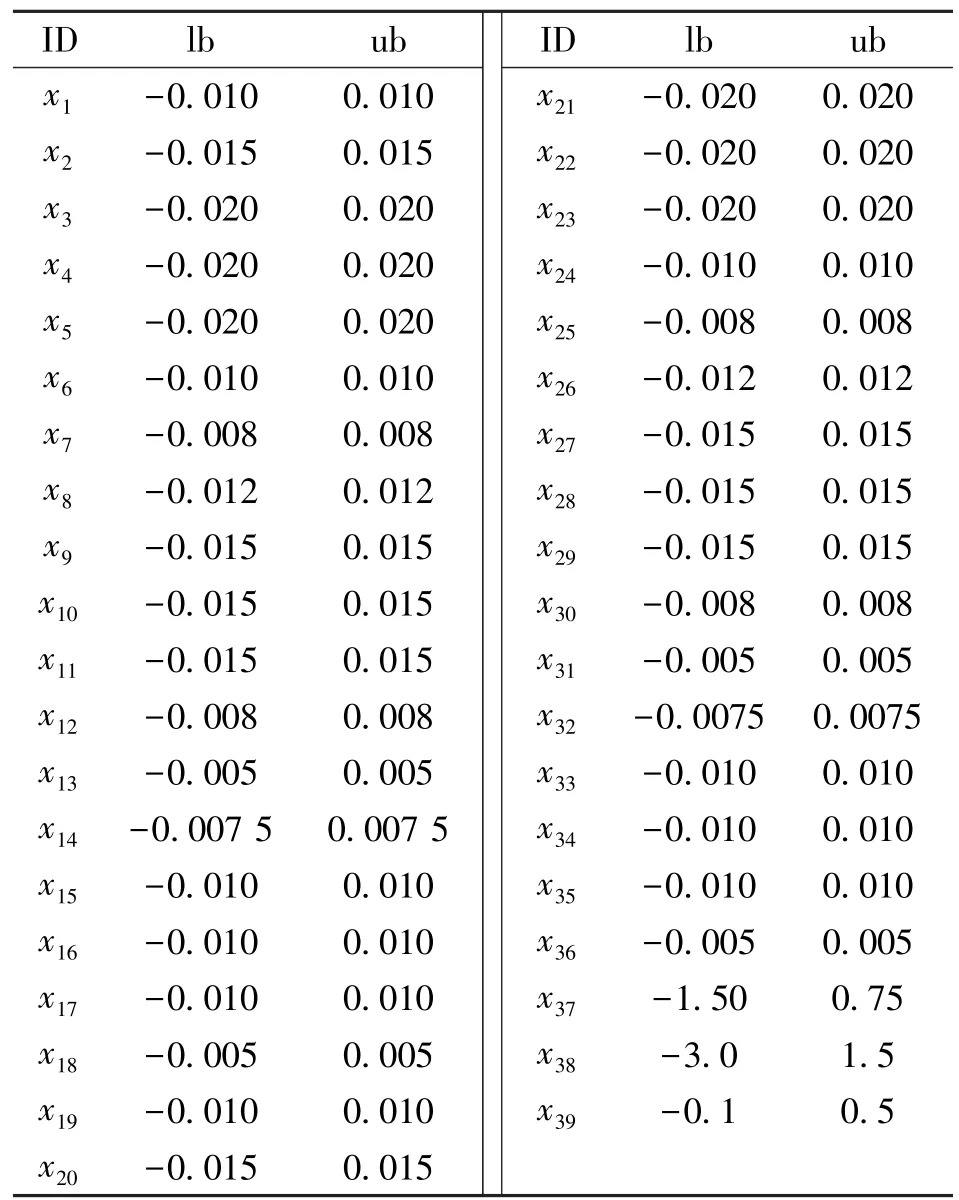
表1　39个设计变量范围

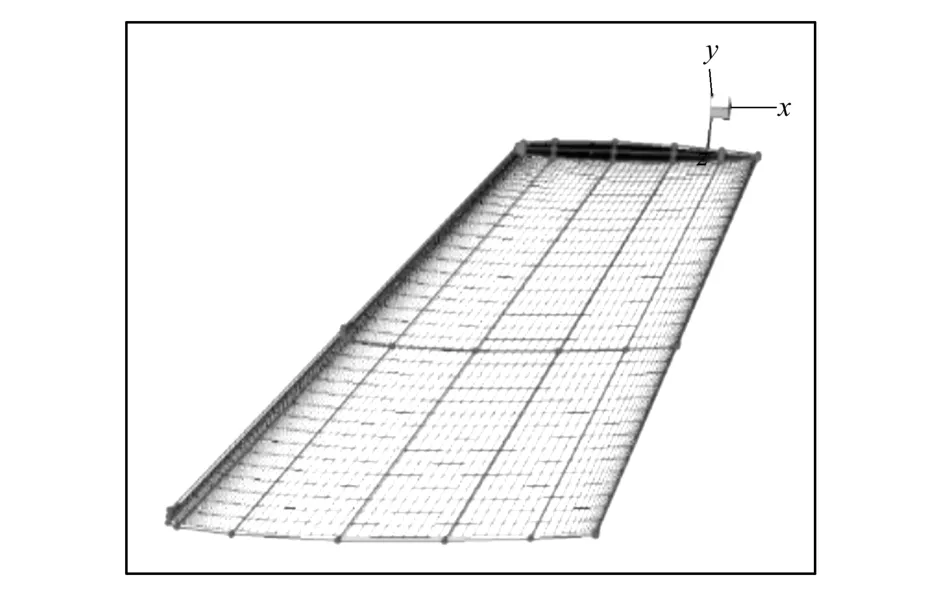
图3　FFD控制框及控制点

3.1基于确定性代理模型的稳健性优化

应用DK代理模型对柔性M6机翼在满足容积约束条件下，考虑马赫数不确定变化范围Ma∈［0.82，0.83，0.84，0.85，0.86］时，进行稳健性优化设计，提高设计点的气动特性，同时改善优化后机翼的阻力发散特性。

优化模型可表述为：

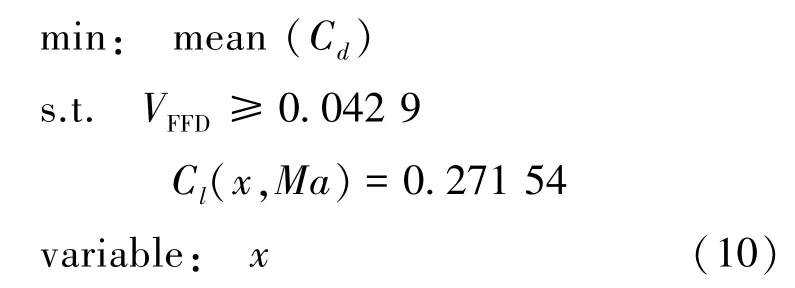
在设计空间内生成869个样本点，选取19个为测试样本点，其余850个构建改进的Kriging代理模型。应用改进的遗传算法每代种群数为300个，进化代数为30代，在保证机翼体积不减小的情况下进机翼的稳健性优化设计。优化结果在3.3节中进行详细讨论。

3.2基于随机代理模型的稳健性优化

基于构建的SK代理模型对M6机翼进行保证容积约束的稳健性优化设计，利用构建的优化系统在给定的约束条件下改善阻力发散特性。设计状态为马赫数范围Ma［0.82，0.83，0.84，0.85，0.86］，优化的目标为降低阻力系数在扰动范围内的均值和方差。优化模型可表述为：

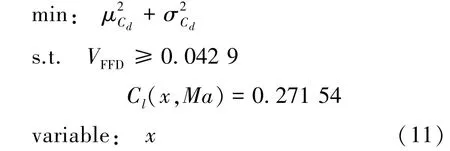
式中

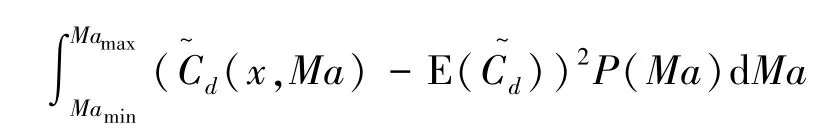
为保证与使用确定性代理模型进行优化设计的采样个数相同，将选用3.1节相同样本点和优化算法。与运用确定性代理模型不同的是，在不同设计变量处进行马赫数变化区间内5次均匀分布重复采样建立随机代理模型，通过在不同设计变量处的均值和方差作为SK模型的输入变量，得到设计变量在未知位置处的响应均值和方差。

选取869个样本点中19个作为测试样本点，用于验证SK代理模型是否合理。图4给出SK代理模型预测的均值、方差与实际计算结果的对比曲线，结果吻合得很好，证明建立的SK代理模型的精度可以满足之后的稳健性优化设计的需求。

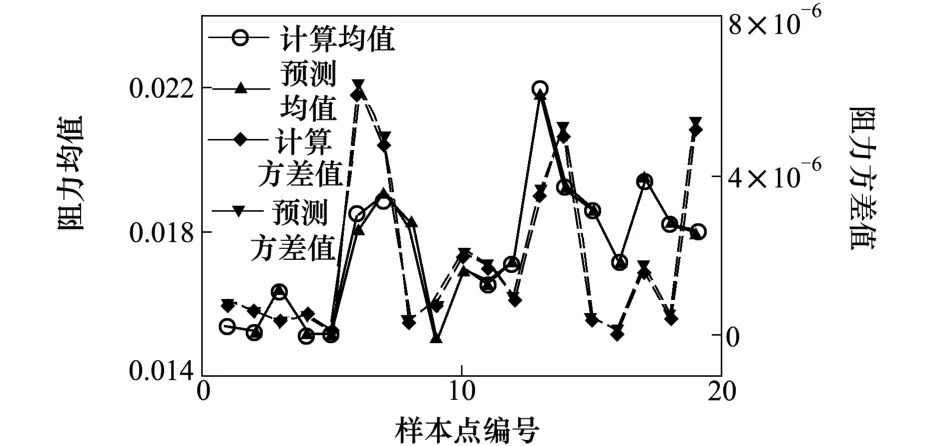
图4　SK代理模型预测的阻力均值与方差

3.3结果分析

图5为优化前后几何模型对比图。

图5　优化前后几何模型对比

可以得出优化后构型的后掠角均增大，而SK模型优化结果的后掠角最大。

图6为阻力发散特性曲线对比可得，2种优化结果在设计点处的阻力特性均得到改善，并且优化后阻力发散特性均得到明显提高。通过DK代理模型和SK代理模型的优化结果对比曲线可得，SK代理模型的结果明显优于DK代理模型，SK模型对随机问题表现出了更强的预测能力。

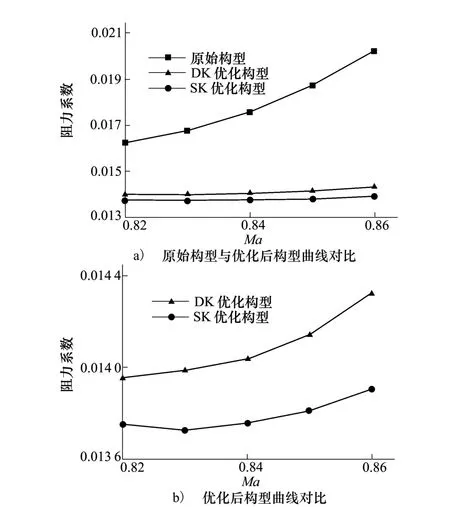
图6　阻力发散特性曲线对比

表2给出DK代理模型优化解在设计点位置阻力降低21.56%。在5个马赫数阻力系数均值降低21.33%，方差降至2.149×10-8。SK模型优化解在设计点位置阻力降低23.30%，在可变马赫数范围为阻力系数均值降低23.23%，方差降至5.543 ×10-9。

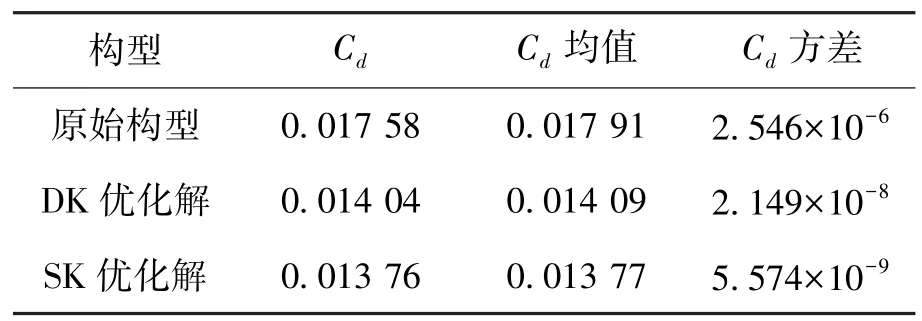
表2　DK、SK代理模型稳健性优化结果对比

图7为0.84马赫数下运用DK代理模型和SK代理模型进行的稳健性优化设计结果在2个典型剖面的压力分布对比，优化构型消除了机翼上表面激波，压力分布恢复平缓。优化后机翼前缘峰值有所降低，有利于阻力发散特性改善有利，应用SK代理模型优化结果的峰值比DK代理模型优化的结果要低。

图8为优化前后机翼考虑柔性变形后无量纲翼根弯矩的对比曲线。由图中可得：采用DK代理模型优化解的翼根弯矩较原始构型有所增加，而采用SK代理模型优化解则明显减小。可以得出，SK代理模型优化后构型没有增加结构的要求下，明显降低了翼根剖面的弯矩。

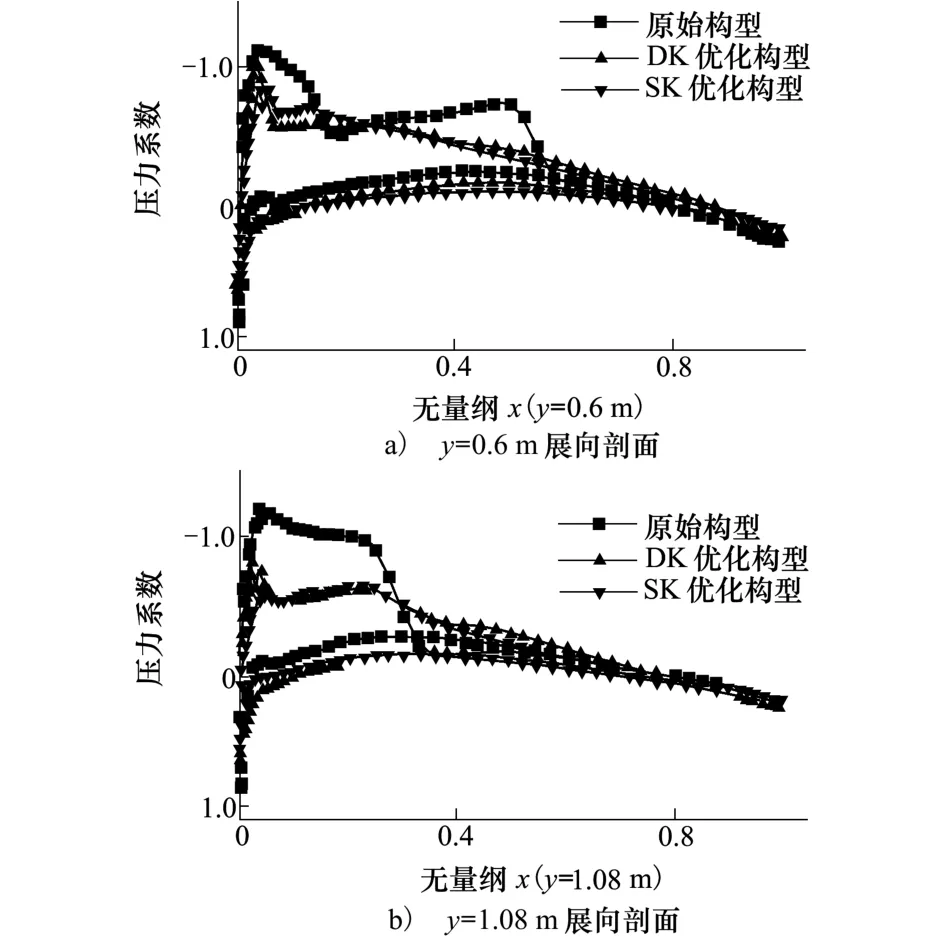
图7　典型剖面压力系数曲线对比图

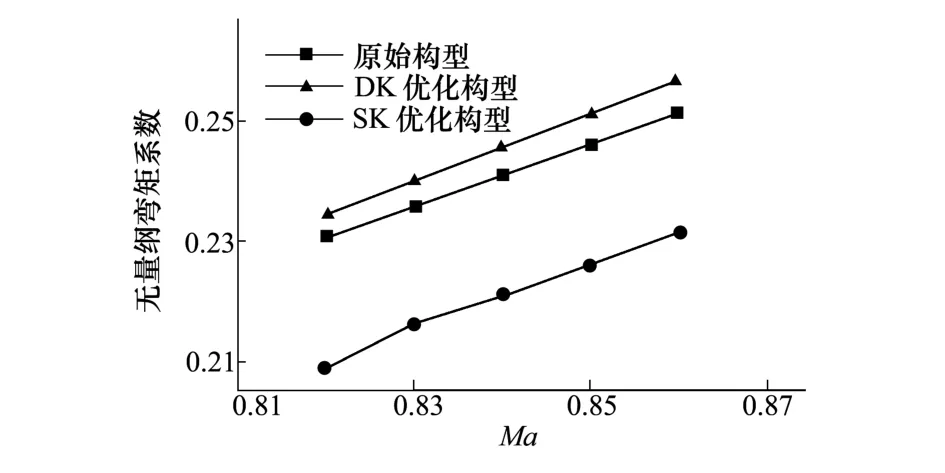
图8　无量纲翼根弯矩对比曲线

4　结 论

通过研究柔性机翼的基于DK与SK稳健性优化设计结果的对比，可看出基于SK代理模型的稳健性优化设计更能有效提高柔性机翼的阻力特性及阻力发散特性。应用SK代理模型在优化过程中考虑不确定因素的存在，可以有效解决稳健性优化设计问题。SK代理模型优化结果较DK代理模型优化结果在设计点处阻力系数减小2.8 counts，在可变马赫数范围内阻力系数均值减小3.2 counts。同时SK代理模型稳健型优化后机翼对翼根弯矩有明显减小。显示出所构建SK代理模型在不确定性问题的研究中较DK代理模型有优势。

［1］ Zang T，Hemsch M J，Hilburger M W，et al.Needs and Opportunities for Uncertainty-Based Multi Disciplinary Design Methods for Aerrospace Vehicles［R］.NASA TM-2002-211462

［2］ Zeeshan Q，Yunfeng D，Rafque A F，et al.Multidisciplinary Robust Design and Optimization of Multistage Boost Phase Interceptor［R］.AIAA-2010-2920

［3］ Yu X，Du X.Reliability-Based Multidisciplinary Optimization for Aircraft Wing Design［J］.Structure and Infrastructure Engineering 2006，2（3/4）：277-289

［4］ Sues R H，Oakley D R，Rhodes G S.MDO of Aeropropulsion Components Considering Uncertainty［R］.AIAA-1996-4062

［5］ Queipo N V，Haftka R T，Shyy W，et al.Tucker Surrogate-Based Analysis and Optimization［J］.Progress in Aerospace Sciences，2005，41：1-28

［6］ Schuelera G I，Jensen H A.Computational Methods in Optimization Considering Uncertainties—An Overview［J］.Computer Methods in Applied Mechanics and Engineering，2008，198（1）：2-13

［7］ Andradottir S.A Review of Simulation Optimization Techniques［C］∥Proceedings of the 1998 Winter Simulation Conference，IEEE，Piscataway，NJ，1998：151-158

［8］ Jin R，Du X，Chen W.The Use of Metamodeling Techniques for Optimization Under Uncertainty［J］.J Struct Multidisciplinary Optim，2003，25（2）：99-116

［9］ Hans Georg Beyer，Bernhard Sendhoff，Robust Optimization—A Comprehensive Survey［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（33/34）：3190-3218

［10］Wang B，Bai Junqiang，Hae Chang Gea.Stochastic Kriging for Random Simulation Metamodeling with Finite Sampling［C］∥39th Design Automation Conference（DAC），Portland，Oregon，2013

［11］Liu Y，Bai J Q，Hua J.Static Aeroelasticity Analysis of High Aspect Ratio wing and the Jig-Shape Design Based on Multi-Block Structural Grid［J］.Advanced Engineering and Materials，2013，302：377-383

［12］刘艳，白俊强，华俊，等.非线性流固耦合分析方法研究［C］∥中国力学大会，2013

Liu Y，Bai J Q，Hua J，et al.An Approach to the Nonlinear Fluid-Structure Coupling Technical［C］∥CCTAM2013，2013（in Chinese）

［13］Journel A G，Huijbregts CJ.Mining Geostatistics［M］.London，Academic Proess，UK，1978

［14］Lamousin H J，Waggenspack W N.NURBS-Based Free-Form Deformations［J］.IEEE Computer Graphics and Applications，1994，11：59-65

Robust Optimization of Flexible Wing Using Stochastic Kriging Surrogate Model

Liu Yan1，Bai Junqiang1，Hua Jun1，2，Liu Nan1，Wang Bo3

1.College of Aeronautics，Northwestern Polytechnical University，Xi′an 710072，China 2.Chinese Aeronautics Establishment，Beijing 100012，China 3.China Academy of Aerospace Aerodynamics，Beijing 100074，China

The stochastic surrogate model method is applied in the robust optimization design of flexible wing.Comparing with deterministic optimization design，robust design can take into consideration the disturbances of design variables and parameters.Therefore，the performance of design results can be kept stable under uncertainties.A High-fidelity fluid-structure coupling solver（coupled Navier-Stokes equations and static structure equations）is used to analyze the deformation and aerodynamic characteristics of flexible wing.In order to enhance optimization efficiency，Stochastic Kriging（SK）surrogate model，which extends deterministic Kriging（DK）surrogate model into stochastic space，is built.The intrinsic uncertainties of data is acquired by finite number of inputs.The robust optimization of flexible M6 wing illustrates that comparied with robust optimization results of DK，the drag coefficient of optimal result of SK has reduced 2.8 counts and the mean values in variable MachNumberrange have reduced 3.2 counts.The optimal result of SK has higher aerodynamic efficiency in design point and better drag divergence characteristics.It is manifested that stochastic surrogate model is favorable in robust optimizationand the SK surrogate model possesses high prediction accuracy.

aeroelasticity，computational fluid dynamics，deformation，design，drag coefficient，elastic deformation，finite element method，flexible wings，flow fields，flow charting，forecasting，genetic algorithms，geometry，Mach number，mean square error，Navier Stokes equations，optimization，pressure distributions，Reynolds numbers，statistics，stochastic models，structural dynamics，robust optimization static aeroelasticity；stochastic Kriging（SK）surrogate model

V211.3 V214.3+2

A

1000-2758（2015）06-0906-07

2015-03-31

国家“973”计划（2014CB744804）资助

刘艳（1988—），西北工业大学博士研究生，主要从事气动弹性分析与多学科优化设计研究。