无人机螺旋自主认知与改出控制器设计
黄汉桥,赵鑫,周欢,王族统
(1.空军工程大学航空航天工程学院,陕西西安 710038;2.西北工业大学 陕西西安 710072)
无人机螺旋自主认知与改出控制器设计
黄汉桥1,2,赵鑫1,周欢1,王族统1
(1.空军工程大学航空航天工程学院,陕西西安 710038;2.西北工业大学 陕西西安 710072)
针对飞行器螺旋改出难题,研究无人机螺旋自主认知与改出控制方法。首先建立基于飞行状态认知的无人机安全控制框架,在此基础上进行无人机螺旋认知与改出控制器设计,分析螺旋成因,根据机载传感器提供的实时飞行参数信息,采用直觉模糊统计判决与决策算法进行螺旋自主认知,最后考虑状态变量控制时序,并设计非线性动态逆控制律,完成无人机螺旋改出的制导控制。仿真结果表明,相对于已有解决策略,所提出的控制方法可以显著缩短螺旋改出所需时间,同时具有较好的动态响应特性。
无人机;螺旋;认知;改出;安全控制;控制器;控制时序;非线性动态逆;统计;决策;动态响应;飞行状态;攻角;角速率;自主;飞行控制
在无人机全空域使用、飞行频次不断增加的情况下,其频频出现撞损、坠毁、失控等安全性事件,飞行问题日益凸显[1]。Leveson在文献[2-3]提出了系统安全性方法论,其中安全被看作是一个控制问题。无人机进入危险飞行状态后,如不采取紧急避险控制,发生安全性事件的可能性较大,特别是无人机进入失速或者螺旋状态。步入螺旋是尾旋的前期表现,2012年6月,美军1架“全球鹰RQ-4A”无人机在例行训练中进入螺旋,最终导致尾旋坠毁,这一事件引起了国内外广泛关注。因此,如何避免无人机进入螺旋和改出螺旋已成为确保无人机飞行安全所亟待解决的问题。
目前关于飞机螺旋的研究,主要集中在有人机领域。美国自20世纪50年代开始进行有人机螺旋改出研究,兰利中心1957年写的《近代飞机设计中尾旋研究现状》中,提出了压杆改出螺旋的设想和理论上的探讨,在后续的飞行表演中,美国飞行员成功运用螺旋改出方法进行了失速和螺旋改出的表演;国内针对有人战斗机飞行特点,制定了一系列螺旋判断及改出方法,形成了不同类型飞机的飞行规范和体制,如对歼六战机,提出“平、中、顺”方法是改出螺旋的最有效方法;文献[4]探讨了螺旋技术在飞行特技中的运用。
然而,国内外对无人机螺旋研究比较少。俄罗斯“搜索”网站2008年12月24日报道:俄罗斯中央空气流体动力学研究所正在开发避免无人机进入螺旋状态的专业技术;文献[5]研究了方向舵卡死无人机步出螺旋的控制律设计,但其针对的是螺旋模态运动,并未考虑大迎角引起的不稳定螺旋和尾旋;目前,尚未发现无人机螺旋改出控制的相关文献与研究。
美国空军研究实验室技术领域专家B.T.Clough指出,自主化的控制是提高无人机飞行安全性的最有效措施[6]。在无人机螺旋改出控制中,实现自主化主要面临以下几方面的问题:①如何实现飞行状态认知,进行及时有效的螺旋判断;②如何把握控制器的控制时序,减少舵面的耦合作用,保证各个舵面效用的最大程度发挥;③如何设计良好的非线性控制律,以保证无人机在大迎角和非线性特性严重的状态下,得到满意的螺旋改出控制效果。
针对上述问题,本文提出基于飞行状态认知的无人机自主安全控制框架,并在此基础上设计螺旋认知与改出控制器。根据无人机螺旋特征,采用直觉模糊统计判决与决策算法进行螺旋认知,基于控制时序与非线性动态逆控制律,完成无人机螺旋改出的制导与控制,最后通过数值仿真验证所提方法的有效性。
1 基于飞行状态认知的无人机自主安全控制框架
1.1无人机自主安全控制框架
无人机自主安全控制,是指无人机在飞行过程中能够依靠无人机系统的感知和认知计算功能,对即将或正在发生的飞行风险进行感知、识别,并自主生成正确规避或者改出策略的控制方法。此方法是认知计算[7-9]在无人机导航控制系统中的具体应用。
无人机利用机载惯导系统、高度计、GPS等传感器对自身飞行参数信息进行测量,测量数据在感知层进行处理,感知层输出的信息耦合到认知决策层进行更进一步的相关处理,通过与知识库的信息进行匹配分析,实现对自身飞行状态的认知,并结合任务和平台特性产生相应的制导决策指令,通过飞行控制系统驱动无人机规避或改出飞行风险。无人机自主安全控制方法框架如图1所示。

图1 基于飞行状态认知的无人机自主安全控制框架
由图1可知,无人机自主安全控制主要包含以下3个部分:飞行状态认知、自主决策和飞行控制。
1)飞行状态认知
飞行状态认知是无人机对来自数据链或机载传感器的飞行参数信息(如速度、高度、姿态角以及姿态角速率等)的感知和识别,进而实现自身状态理解与判断。一般而言,这些信息具有大量性、多样性以及复杂性。无人机将获得的新信息(表现为短时记忆)与先验信息(表现为长期记忆)进行数据融合,依据系统知识库,对数据信息进行自主分析、理解与认知。
2)自主决策
当认知无人机所处飞行状态后,系统基于认知和决策知识库做出决策,自主切换到对应控制模块,在此基础上进行实时飞行态势评估,准确把握系统的控制时序,并给定相应的输出。
3)飞行控制
针对每一种飞行状态,控制模块包含相应控制律,控制律设计主要考虑飞行状态特征与操纵舵效。无人机在飞控系统作用下,逐步脱离危险飞行状态。
1.2无人机螺旋认知与改出控制器结构
根据上述无人机自主安全控制框架,设计的螺旋自主认知与改出控制器结构如图2所示。

图2 无人机螺旋认知与改出控制器结构
首先采用一定的方法认知无人机螺旋状态,根据螺旋状态中的实时飞行参数,从控制时序和控制律出发,完成无人机的制导控制,实现无人机的安全飞行。
2 无人机螺旋认知
在实际飞行过程中,无人机面临的飞行风险状态主要包含失速、偏离(变状态)、失速性滚转、螺旋等[10]。因此,无人机进入非正常飞行状态后,必须迅速判断出飞机所处的风险状态类别,然后自主进行规避或改出的相应操作。
2.1螺旋成因分析
螺旋是无人机进入失速后发生的同时绕自身三轴自动旋转,并沿着一条小半径螺旋形轨迹急剧下降的一种非正常运动。无人机失速后发生的机翼自转或方向发散是形成螺旋的根本原因。
1)机翼自转
无人机机翼上的法向力系数Cz可表示为:

对于小型低速无人机,升力系数Cy较大,而阻力系数Cx较小,因此可以用升力系数分析大迎角滚转阻尼的变化。
无人机进入大迎角飞行,当产生滚转时,下沉机翼迎角增大,升力系数反而减小,上扬机翼迎角减小,升力系数反而增大,此时机翼滚转阻尼会发生变号,阻尼作用变成助滚作用,形成机翼自转。
2)方向发散
无人机进入失速后可能产生机头自动偏转的现象,这是由于无人机丧失了方向静稳定性所致。无人机出现方向发散后,侧滑引起两翼的升力差使无人机在偏转的同时发生滚转,偏滚中产生俯仰惯性力矩,将使无人机迎角进一步增大。
3)滚转发散
滚转发散通常发生在无人机处于负迎角飞行状态下。在负迎角状态下,横侧静稳定度时,无人机具有横侧静稳定性;当超过负的失速迎角,即横侧静稳定度时,无人机丧失横侧静稳定性,此时易导致滚转发散。
2.2螺旋认知方法
无人机进入螺旋飞行状态,飞行参数交叉发生剧烈变化,为了将无人机主观知识库与客观世界的随机性有机地结合在一起,采用直觉模糊统计判决与决策方法[11]进行螺旋认知。
设五元组{S,D,X,P(si),U(dj,si)},其中:S= {s1,s2,…,sn}是无人机飞行参数的集合,主要包含速度、高度、姿态角,姿态角速率等,D={d1,d2,…,dm}是飞行状态判决决策集合,主要包含失速、偏离、失速性滚转、螺旋等,X={x1,x2,…,xl}是追加的信息源,如系统误差、环境扰动等,其中每一条信息xk(k=1,2,…,l)对si的影响,P(si)表示si发生的概率,U(dj,si)为评价函数,即飞行参数为si时,判决为di取得的效果。

基于上述判决决策方案,即可判断出螺旋与否,实现飞行状态认知。
3 无人机螺旋改出控制
准确认知进入螺旋后,无人机切换到螺旋改出控制模块,控制器根据实际的螺旋动态,自主进行螺旋改出控制。
3.1状态变量控制时序与给定输出
无人机在失速飞行时,各个操控舵面存在耦合作用和位置约束,会出现舵面效用降低的情况[12-13],因此在螺旋改出过程中,很难对无人机系统中的各个状态变量同时进行有效控制。有人机螺旋改出的实践证明,比较有效的方法必须首先制止旋转。如果带着很大的旋转角速率控制迎角,推杆产生的操纵力矩不足以克服较大的上仰惯性力矩,不仅迎角减不下来,反而会因为推杆产生的助滚、偏力矩,加快无人机旋转,同时姿态角的控制主要依靠副翼,而副翼在大迎角下的操纵效率偏低,因此控制姿态角的前提是无人机处于较小迎角状态。
综上所述,在改出螺旋过程中,必须准确把握控制时序问题,给定对应输出,以进行相关变量控制。这样就可以防止螺旋更加发散,并最大限度发挥操纵舵面的作用。螺旋改出的控制时序如下:
Step 1 认知进入螺旋,切换至螺旋控制模块,给定角速率输出,进行减缓旋转角速率控制;
Step 2 当无人机偏转与滚转减慢后,给定迎角输出,进行迅速减小迎角控制;
Step 3 当迎角减小到临界迎角以下,给定姿态角输出,进行旋转姿态角控制;
Step 4 无人机停止偏转和滚转,达到期望姿态角,进行俯冲增速控制;
Step 5 当速度增大到一定程度,执行退出俯冲控制程序。
为研究简便,当无人机停止旋转并达到期望姿态角,即可认为已经完成螺旋改出。
3.2非线性动态逆控制律
无人机处于螺旋飞行状态时,非线性特性特别明显,为此在设计控制律时,不能在小扰动线性化的基础上进行三通道独立设计。在飞行器的设计中,使用较广的方法是非线性动态逆控制[14,15],本文利用奇异摄动理论结合动态逆方法设计无人机非线性动态逆控制律。
无人机的六自由度模型[16]是包含12个状态变量的非线性动力学系统,12个状态变量分别为

式中:p、q、r分别为滚转角速率、俯仰角速率、偏航角速率;α、β、μ分别为迎角、侧滑角、滚转角;V、χ、γ分别为速度、偏航角、航迹倾斜角;X、Y、Z分别为无人机质心位置在地面坐标系中的投影坐标。
根据无人机的运动规律和奇异摄动理论进行时标划分,将状态变量分成快速变量[p q r]T、中速变量[α β μ]T、慢速变量[Vχγ]T或[X Y Z]T,把无人机非线性方程组分解为3个不同时间尺度的子系统。大系统中各子系统之间按照时标分离的原则选择不同频带,在此基础上,使用状态反馈型动态逆控制方法[17]可使三组状态量的控制获得一阶线性解耦控制结构,而且3个快慢不同的回路可以独立设计。
在无人机螺旋飞行与改出控制过程中,关心的只是快速变量与中速变量,因此主要进行快速回路与中速回路控制律设计,非线性动态逆控制律结构如图3所示。
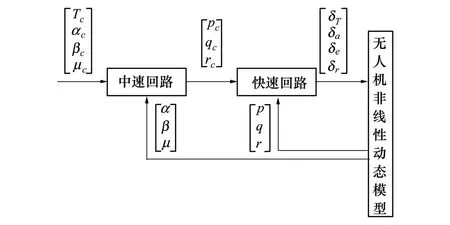
图3 非线性动态逆控制律结构
1)快速回路控制律
快速回路主要实现对p,q,r的控制,即根据给定角速率输入pc,qc,rc,求解控制舵偏量。快速回路方程写为仿射形式,即为

式中,x1=[p q r],x为8个无人机状态组成的向量,定义为

u是3个控制舵面偏角组成的向量,定义为

u是快速回路的输出,同时也是无人机对象的控制量输入。
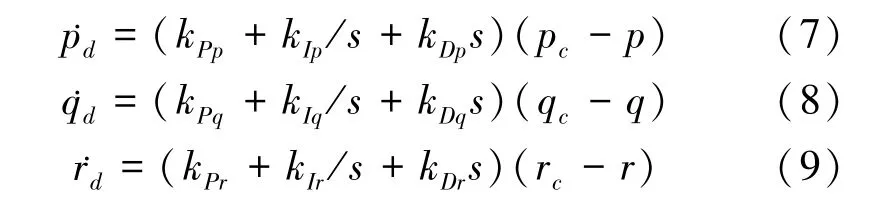
式中,变量KP∗、KI∗、KD∗为快速回路的PID反馈增益[18],其取值在20~30 rad/s。
则控制输入u应具有如下形式

结合无人机六自由度运动方程,展开(10)式,可得

式中
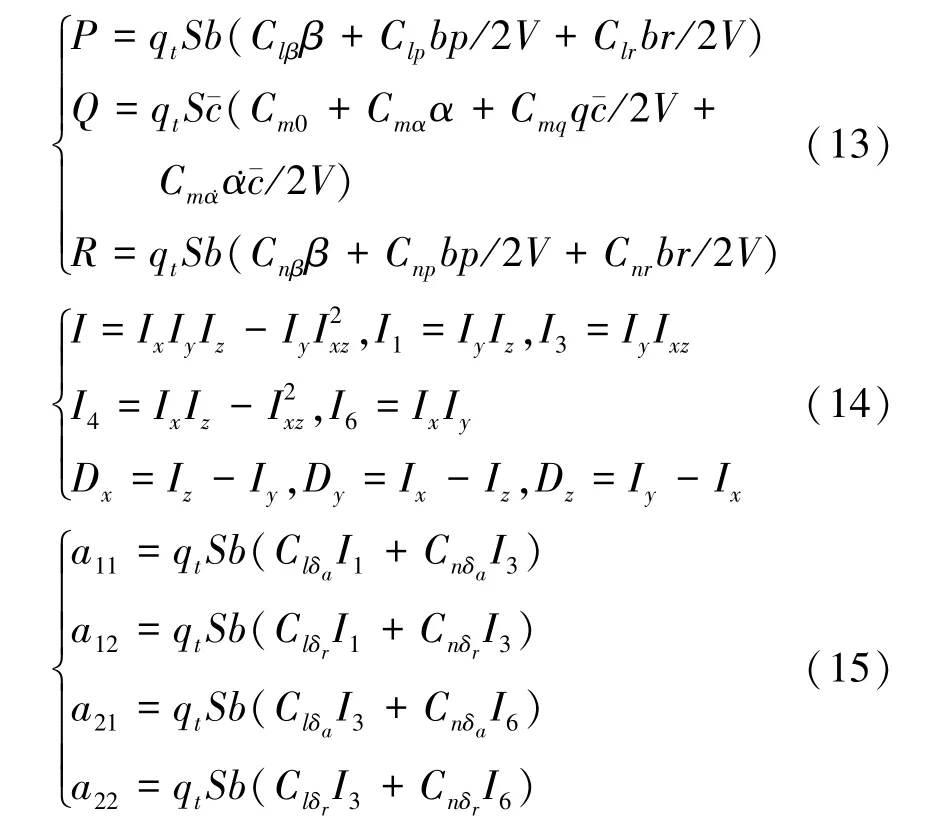
(7)式~(10)式结合在一起组成完整的快速回路,实现对无人机快速回路控制律设计。
2)中速回路控制律
中速回路主要实现对α、β、μ的控制,即根据给定姿态角输入αc、βc、μc,求解输出pc、qc、rc。忽略舵面偏转产生的直接力,其对应的无人机方程为

令快速回路期望角速率α□、β□、μ□的闭环动态响应具有如下形式

式中,kα、kβ、kμ为中速回路的带宽,其取值在5~10rad/s之间。
按动态逆思想得到控制指令输出

结合无人机六自由度运动方程,展开(18)式,可得

式中

(17)式~(18)式结合在一起组成完整的中速回路,实现对中速回路控制律设计。
4 数字仿真及分析
仿真样例无人机为以色列航空工业公司的IAI Pioneer小型无人机,具有固定翼翼型,其临界迎角为30°。选择高度2 000 m,巡航速度42 m/s的平飞状态作为无人机的初始运动状态。
仿真1 螺旋认知
首先在断开螺旋改出控制模块,即自动驾驶仪控制条件下,对无人机进入螺旋和螺旋认知进行仿真。
在初始状态下,对无人机实施“大拉杆”操作,无人机姿态角与角速率变化如图4a)~图4c)所示。

图4 无人机进入螺旋的动态过程
由图4输出结果,迎角发生周期性变化,均值大于临界迎角。令Q1表示“无人机进入失速状态”,Q2表示“无人机进入螺旋状态”,Q3表示“无人机进入失速性滚转”,Q4表示“无人机进入偏离状态”;M1表示“迎角到达临界角附近”,M2表示“偏航角速率增大”,M3表示“滚转角速率较大且滚转角大于某特定值”。
在t=4 s时,根据得到的条件概率,计算直觉模糊决策方案对直觉模糊时间的效用:

根据区间数比较方法,有

因此,无人机自主认知t=4 s时进入螺旋状态。在t=60 s内,无人机三维飞行轨迹如图4d)所示,可知,无人机螺旋自主认知结果与实际进入螺旋相符。
仿真2 自主改出控制方法(ARC)
在接通螺旋改出控制模块条件下,对无人机改出螺旋进行仿真。
无人机初始运动状态及其进入螺旋操作同上,在所设计的螺旋改出控制器作用下,无人机姿态角与角速率变化如图5a)、图5b)、图6c)所示。
控制参数设置为:
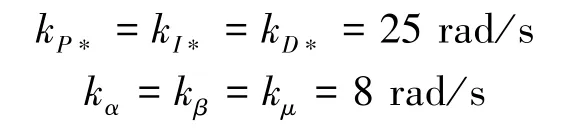
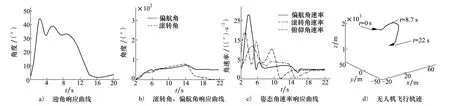
图5 无人机在ARC作用下的螺旋改出过程
由图5可知,t=4 s时,无人机认知进入螺旋,自动切换到螺旋改出模块并给定pc=0,qc=1,rc= 0,控制旋转角速率;t=8.7 s时,无人机认知旋转减慢,给定αc=5,βc=0,μc=50,控制迎角与姿态角;t =14 s时,无人机认知迎角变小,给定αc=4,βc=0,μc=0,t=19.8 s时,无人机停止旋转,达到期望姿态角,有效改出螺旋,即可进入退出俯冲控制模块,其螺旋改出三维飞行轨迹如图5d)所示。
仿真3 “平中顺”改出控制方法(FMP)
当无人机进入螺旋后,模拟地面操作人员,采用“平置方向舵,中立升降舵,顺压副翼”(“平中顺”)方法进行螺旋改出控制,无人机姿态角与姿态角速率变化如图6a)、图6b)、图6c)所示,螺旋改出三维飞行轨迹如图6d)所示。

图6 无人机在FMP作用下的螺旋改出过程
由图6可知,“平中顺”方法虽然也可以改出螺旋,但是该控制方法下的改出所需时间过长,这将导致无人机损失高度过大,从而引起坠毁。
仿真4 未考虑“控制时序”的自主改出控制方法(ARCNCS)
在无人机螺旋自主改出控制器设计中,不考虑状态变量控制时序,直接给定期望输出,在非线性动态逆控制律作用下进行螺旋改出控制,无人机姿态角与姿态角速率变化如图7a)、图7b)、图7c)所示,螺旋改出三维飞行轨迹如图7d)所示。

图7 无人机在ARCNCS作用下的螺旋改出过程
由图7可知,当无人机螺旋自主改出控制不考虑“控制时序”时,改出时间延长,同时姿态角及角速度响应出现振荡,使得无人机在某个阶段的螺旋特性更加复杂。
在ARC、FMP、ARCNCS 3种控制方法作用下,螺旋改出所需时间如表1所示。

表1 3种控制方法下的螺旋改出所需时间
从表1统计结果可以看出,3种控制方法均可以使无人机改出螺旋,但ARC方法具有最好的控制效果。
对上述4个仿真结果进行对比分析可知,本文采用的无人机螺旋认知方法能够实现对无人机进入螺旋状态的认知,所提的自主改出控制方法能克服其他方法的缺点,较为有效地解决了无人机螺旋改出问题。
5 结 论
本文针对无人机螺旋改出问题进行研究,设计了无人机螺旋自主认知与改出控制器。提出基于飞行状态认知的无人机自主安全控制方法,在此基础上采用直觉模糊统计判决与决策算法认知螺旋,并从控制时序与控制律出发,完成了螺旋改出的制导与控制。仿真结果验证了所提控制方法的有效性,表明该方法可以及时完成螺旋认知,并显著缩短改出所需时间,同时具有较好的动态特性。
[1] Loh R,Bian Y,Roe T.UAVs in civil airspace:safety requirements[C]//IEEE Aerospace and Electronic Systems,2009:5-17
[2] Leveson,N.Safeware:System Safety and Computers[M].Addison-Wesley,New Jersey,1995
[3] Leveson N.A New Accident Model for Engineering Safer Systems[J].Safety Science,2004,42(4):237-270
[4] 马庭亮.螺旋技术在飞行特技中的运用探讨[J].技术与市场,2011,18(7):91-92
Ma Tingliang.The Application Discussion of Spiral Technology on Aerial Acrobatics[J].Technology and Macket,2011,18 (7):91-92(in Chinese)
[5] 陈淑琴,赵文成,席剑辉.方向舵卡死无人机步出螺旋运动控制律的设计[J].电光与控制,2010,17(9):57-59
Chen Shuqin,Zhao Wencheng,Xi Jianhui.Control Law Designed for UAV to Step out Spiral Motion When Rudder Deadlock Happens[J].Electronics Optics&Control,2010,17(9):57-59(in Chinese)
[6] Clough B T.Unmanned Aerial Vehicles:Autonomous Control Challenges,a Researcher′s Perspective[C]∥2ndAIAA“Unmanned Unlimited”Systems,Technologies,and Operations,San Diego,California,2003
[7] Huang X,Huang H,Liao B,et al.An Ontology-Based Approach to Metaphor Cognitive Computation[J].Minds and Machines,2013,23(1):105-121
[8] Mark Bishop J,Erden Y J.Computational Creativity,Intelligence and Autonomy[J].Cognitive Computation,2012,4(3):209-211
[9] Squartini S,Hu S,Liu Q.Advances on Brain Inspired Computing[J].Cognitive Computation,2013,5(2):161-163
[10]Gomzin A V,Fesenko E V,Shataev V G.Spiral Descent of an Unmanned Aerial Vehicle[J].Russian Aeronautics,2009,52 (3):277-283
[11]樊雷,雷英杰.直觉模糊统计判决与决策[J].控制与决策,2011,26(3):356-362
Fan Lei,Lei Yingjie.Intuitionistic Fuzzy Statistic Adjudging and Decision-Making[J].Control and Decision,2011,26(3):356-362(in Chinese)
[12]陈勇,董新民,薛建平,等.多操纵面飞控系统约束自适应控制分配策略[J].系统工程与电子技术,2011,33(5):1118-1123
Chen Yong,Dong Xinmin,Xue Jianping,et al.Constrained Adaptive Control Allocation for Multi-Effector Flight Control System [J].System Engineering and Electronics,2011,33(5):1118-1123(in Chinese)
[13]Dyhr J P,Morgansen K A,Daniel T L,et al.Flexible Strategies for Flight Control:an Active Role for the Abdomen[J].The Journal of Experimental Biology,2013,216(9):1523-1536
[14]Sieberling S,Chu Q P,Mulder J A.Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction[J].Journal of Guidance,Control,and Dynamics,2010,33(6):1732-1742
[15]Shu Y,Tang S.Integrated Robust Dynamic Inversion Design of Missile Guidance and Control Based on Nonlinear Disturbance Observer[C]∥20124thInternational Conference on Intelligent Human-Machine Systems and Cybernetics,2012:42-45
[16]韩英华,范彦铭.基于非线性动态逆的无人机自动着陆控制系统[J].航空学报,2008,5(增刊):66-71
Han Yinghua,Fan Yanming.Control System of Automatic Landing of UAV Based on Nonlinear Dynamic Inversion[J].Acta Aeronautica Astronauotica Sinica,2008,5(Suppl):66-71(in Chinese)
[17]Reiner J,Balas G J,Garrard W L.Flight Control Design Using Robust Dynamic Inversion and Time-Scsle Separation[J].Automatica,1996,32(11):1493-1504
[18]Du D J,Fei M R,Hu H S.Two-Layer Networked Learning Control Using Self-Learning Fuzzy Control Algorithms[J].Chinese Journal of Scientific Instrument,2007,28(12):2124-2131
Autonomous Cognition and Recovery Controller Design of UAV Spiral
Huang Hanqiao1,2,Zhao Xin1,Zhou Huan1,Wang Zutong1
1.Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi′an 710038,China 2.Northwestern Polytechnic University,Xi′an 710038,China
Aiming at dealing with the spiral recovery puzzle of aerial vehicles,we put forward an autonomous spiral cognition and recovery control method of the unmanned aerial vehicle(UAV).First of all,the safety control framework of unmanned aerial vehicles(UAV)based on flight state-cognition is built and the autonomous spiral cognition and recovery controller is designed.Then,the spiral factors are analyzed and the spiral state is recognized by using intuitive fuzzy statistic adjudging and decision-making algorithm according to timing flight variables information afforded by airborne sensors.Finally,the control scheduling of state variables is considered,and nonlinear dynamic inversion control laws are designed,which accomplish the guidance and control of the UAV spiral.Simulation results and their analysis suggest that,compared with the existing strategies,the proposed control method can decrease the time needed for spiral recovery evidently and meanwhile has good dynamic response characteristics.
aneroid altimeters,angle of attack,angular velocity,computer simulation,control,control surfaces,controllers,damping,data fusion,decision making,degrees of freedom(mechanics),design,drag coefficient,dynamic response,efficiency,electronic guidance systems,errors,fixed wings,flight control systems,frequency bands,global positioning system,inertial navigation systems,measurements,probability,real time control,safety engineering,scheduling,sensors,statistics,time series,unmanned aerial vehicles(UAV),velocity;cognition,control law,control scheduling,flight state,nonlinear dynamic inversion(NDI),recovery,safety control,spiral statistic adjudging.
V249
A
1000-2758(2015)06-0879-08
2015-02-18
国家自然科学基金(71501184)与航空科学基金(20155196022)资助
黄汉桥(1982—),西北工业大学校友、博士后,空军工程大学讲师,主要从事无人飞行器作战系统与技术、无人作战飞机自主攻击技术等研究。

