向列相液晶弹性各向异性诱导液晶盒产生漏光的研究

王永超，张志东，周 璇

（河北工业大学理学院，天津300401）

向列相液晶弹性各向异性诱导液晶盒产生漏光的研究

王永超1，张志东2∗，周 璇3

（河北工业大学理学院，天津300401）

为了阐述具有体缺陷结构的向列相液晶盒在暗态出现漏光的原因，以及边界锚定条件对漏光的影响，首先，建立了3个向列相液晶盒模型，它们具有不同的初始指向矢排布.接着，基于Landau-de Gennes理论，通过对指向矢场的缺陷动力学计算，得到液晶盒截面内平衡态的指向矢分布.最后，使用琼斯矩阵法将该截面内的指向矢分布以透过率的形式表示出来.模拟结果显示，在无外场条件下，当向列相液晶的弹性常数满足L2/L1≥1（K22/K11≤2/3）时，具有体缺陷结构的液晶盒展现出了自发的扭曲结构，导致了漏光的出现.且漏光强度随着缺陷结构和边界条件的不同而不同.本文模型很好地解释了体缺陷造成液晶盒在暗态出现漏光的原因，且模拟结果与工业生产过程中观察到的现象是一致的.

体缺陷结构；漏光；Landau-de Gennes理论；自发扭曲形变

1　引 言

向列相液晶的弹性常数在显示应用技术中有着重要的作用，不仅表现在显著影响显示器件的电光特性，如视角、透过率等，而且在一定条件下能够使指向矢产生扭曲形变.在向列相液晶微滴中，当扭曲弹性常数较小时，能够诱导指向矢产生巨大的手征对称性破缺，这一现象可以用弹性自由能密度中较大的弹性各向异性来解释［1］.根据Williams［2］和Lavrentovich和Sergan的研究［3］，当扭曲弹性常数（K22）与展曲弹性常数（K11）和弯曲弹性常数（K33）相比较足够小时，分布在球形液晶微滴中，具有沿面锚定的指向矢的手征对称性将被破坏.后来通过实验证实，当弹性常数满足K33/K11≤2.32（1-K22/K11）时，具有双极结构的热致液晶微滴中发生自发扭曲［3-5］.此外，根据Atherton和Sambles的研究［6］，当向列相液晶的扭曲弹性常数分别小于展曲弹性常数和弯曲弹性常数时，在沿面锚定和垂面锚定交替分布的周期表面上，指向矢能够发生自发的取向转变.

近些年来，对于单轴向列相液晶中缺陷的研究已经引起了人们广泛的兴趣［7］.缺陷在新型显示设备中扮演者重要的角色，它们能够在无外场条件下调节稳态之间的转变［8］.有些缺陷在一些显示应用技术中是不可避免的，例如，在多畴显示应用技术中出现的向错线（disclination lines）.虽然这些向错线在低电压下降低了显示器的对比度，但是这种影响是微乎其微的，因为此时显示器处于亮态［9］.然而，缺陷在某些显示技术中的影响是不容忽略的.随着TFT-LCD技术的日益成熟，人们对显示器的显示性能的要求也在不断提高，这激起了人们对显示画面出现的不良现象的研究，如液晶面板在暗态画面下显示区域内发生的微小漏光［10］.此外，液晶盒中的有些缺陷对显示器的影响更加明显，例如体缺陷造成的漏光.液晶中的体缺陷是因为较大的弹性自由能被限制在较小的区域内而产生的［11］，其具体形成途径很多.例如，由于电极形状不均匀而在电极附近形成的缺陷核就可归类为体缺陷的一种［12］.体缺陷造成漏光的机理比较复杂，在本文中我们仅从一个角度对体缺陷造成液晶盒出现漏光的机理进行了探索.通过建立模型研究了具有不同体缺陷结构的向列相液晶盒中指向矢的扭曲形变与弹性各向异性之间的关系，并且运用琼斯矩阵法把指向矢的扭曲形变用液晶盒在暗态时的透过率曲线定量的表示出来.

2　几何模型和光学测量

我们建立了3个向列相液晶盒模型来阐述它们在暗态下出现漏光的原因，它们具有不同的体缺陷结构，我们把它们分别称之为cellⅠ，cellⅡ和cellⅢ，如图1所示.在初态，cellⅠ的左半部分是沿面锚定，右半部分是垂面锚定，指向矢的初态分布如图1（a）所示.cellⅡ是一个混合排列向列相液晶盒，它包含两个旋转角度分别为±π/2的兼并结构，如图1（b）所示.cellⅢ是一个均匀的混合排列向列相液晶盒，初态时盒内没有缺陷存在，如图1（c），它主要作用是作对比研究.

图1　向列相液晶盒模型:（a）cellⅠ；（b）cellⅡ；（c）cellⅢFig.1　Schematic diagrams of the NLC cells:（a）cellⅠ；（b）cellⅡ；（c）cellⅢ

我们假设向列相液晶被限制在间距为d的两基板之间.把上下基板分别置于笛卡尔坐标系的z=±d/2处，基板沿x方向和y方向的长度dx和dy远大于盒厚.在模拟中，我们用θ和φ分别描述指向矢的倾斜角和扭曲角，并且假设初始时刻所有指向矢都平行于y-z平面，因此，初始时刻所有的扭曲角都为零.为了简化计算，我们假设我们所研究的向列相样本与x方向无关.因此，我们可以选取液晶盒的一个垂直于x方向的截面来阐述平衡态指向矢的分布.参考David等人的研究方法［13］，把液晶盒置于两个正交的偏振片中间，让一束自然光垂直照在入射偏振片上，我们通过测量出射偏振片的透过率就能够分析指向矢在液晶盒内的分布情况.因为初始时刻所有指向矢都平行于y-z平面，因此初始时刻测得所有模型的透过率为零.在平衡态一旦指向矢发生扭曲，偏离开y-z平面，漏光就会被检测到，如图2所示.

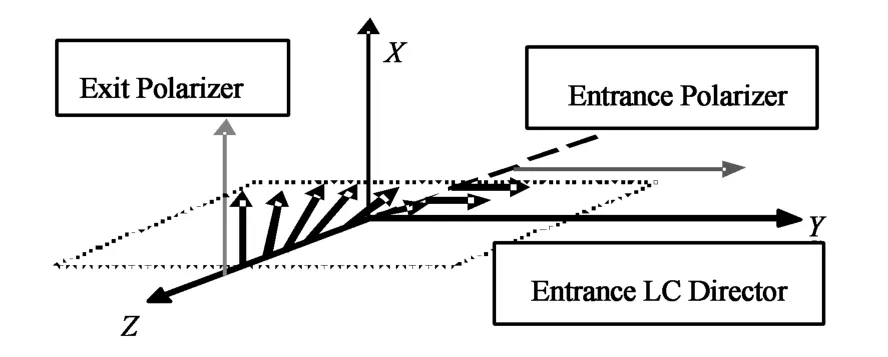
图2　指向矢扭曲形变的测量装置示意图Fig.2　Schematic diagram of measuring the twist deformation of the director

3　理论方法

为了得到含有体缺陷的液晶盒中指向矢在平衡态的分布，首先我们需要计算系统吉布斯自由能［7］.由于Oseen-Frank方程的矢量方法不能够解决含有缺陷的样本，因此我们使用de Gennes的序参数的张量表示来计算系统的平衡态［14］.然后，基于Landau-de Gennes理论，我们使用二维有限差分迭代的方法来计算向列相液晶指向矢场的缺陷动力学和拓扑非平衡态之间的转化［15］.

3.1自由能密度

用二阶对称无迹的序参数张量Q来描述液晶的取向序.在主轴系中，序参数张量可以表示为［16］:

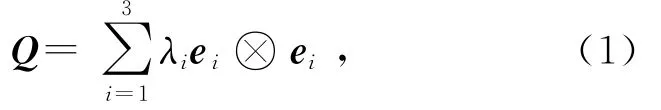
其中:λi和ei分别为Q的第i个本征值和本征矢.在各向同性相中，Q为零阶张量.当系统处于单轴态时，Q的两个本征值相等，可以表示为

其中:S为向列相单轴标量序参数，n为指向矢，I为单位张量.

在没有外场条件下，系统的吉布斯自由能一般包括本体自由能项、弹性自由能项和表面自由能项.当考虑介电效应和挠曲电效应的影响时，液晶系统的Landau-de Gennes自由能可以表示为

其中:V和σ分别表示样本在三维空间所占的体积和所接触的表面积.各物理量的定义及意义如下:

本体自由能密度定义为:［16-17］

弹性自由能密度用序参数的梯度形式表示:

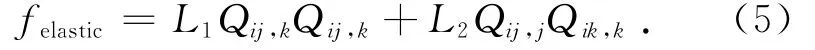
它是液晶取向序的不均匀引起的弹性自由能密度，依赖于序参数张量Q的空间变化率.与Frank弹性理论相比较，我们得到Li和Kii之间的对应关系，

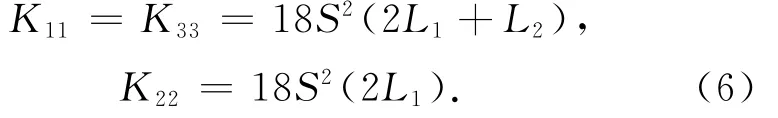
fdielectric项的一般表达式为

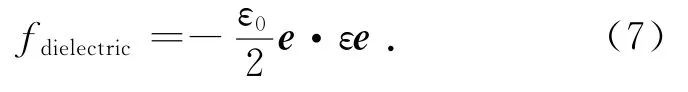
它描述了当给液晶体系施加一个外部电场时，在电场作用下由于指向矢取向改变而引起的自由能的变化，代表着介电效应对自由能的贡献.其中:ε0为真空中介电常数；ε是介电张量，它描述了向列序局部各向异性对电场的响应，它的一般表达式为:

这里εi=（ε∥+2ε⊥）/3和εa=（ε∥-ε⊥）/ 3Seq分别是介电各向同性常数和介电各向异性常数，本文选取εa＞0的材料作为研究对象.假设e垂直于基板表面并且沿z轴方向，即e=Eze，那么fdielectric项可以重新写成下面的形式:

fflexo项是挠曲电效应对自由能密度的贡献［18］；

电场与液晶之间的相互作用除了介电效应之外，还有一种重要的效应，即挠曲电效应.它描述了在电场作用下液晶体系产生极化能的大小.其中都是挠曲电系数，Ei是电场强度沿各坐标轴方向的分量.

fsurface是表面自由能密度项，它描述接近基板的液晶层与基板之间的相互作用

其中:WS=W/S2eq是锚定强度系数，W是Frank弹性理论中的锚定强度系数，Qs是表面处易取向的张量序参数［19］.

3.2约化变量

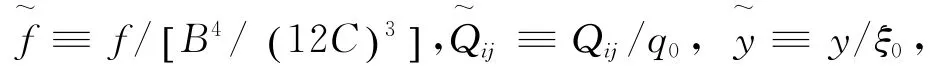
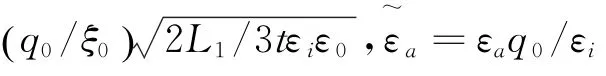
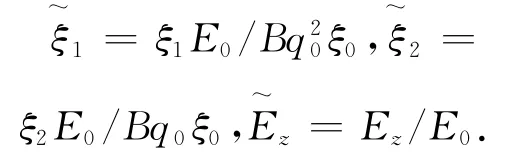
至此方程（9）～（11）可简化为如下形式:

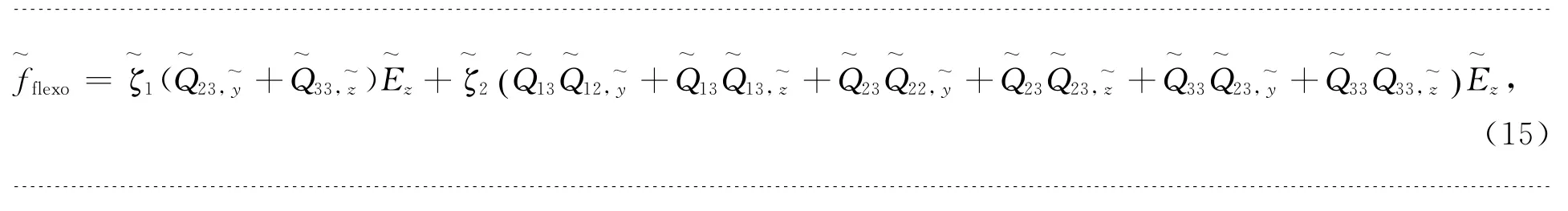
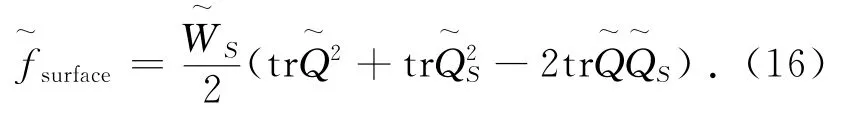
通过上述约化过程，约化后的单轴序为

并且约化后总自由能密度函数表达式为:

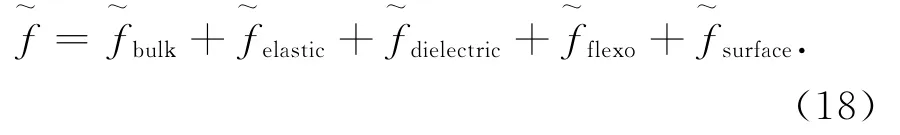
3.3数值方法

把上述3个模型用第二部分给出的边界条件分别进行松弛计算，即利用动力学方程，让序参数张量Q（r，t）在一定初始状态下随时间演化，得到其平衡态结果.标量序参数S和指向矢n的值分别从Q中最大本征值和最大本征值对应的本征矢得到.序参数张量Q的动力学方程可以写为［21-22］:

已知Q的稳定解必须满足方程（19），且本文中的数值计算过程都是使用约化后的变量和方程进行的，所以我们得到了方程（19）的约化形式:

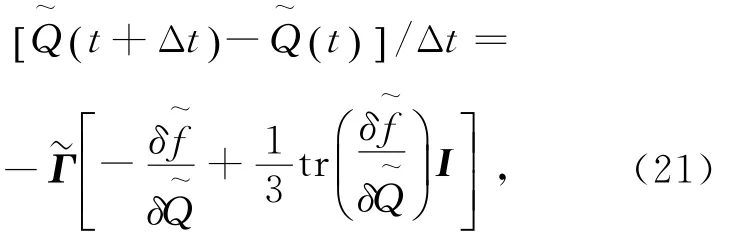
其中:

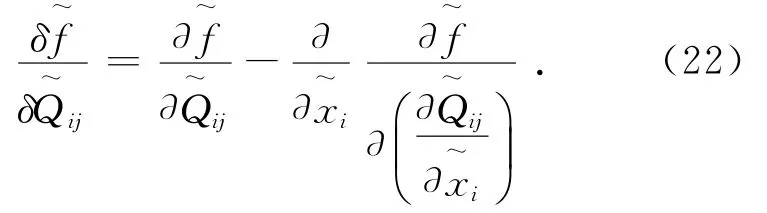
在数值计算中，我们发现给出1×10-6s的时间步长足以保证数值过程的稳定性.此外，运行2×106步，系统足以达到平衡态.

4　数值结果

4.1不同表面条件下cellⅠ中的漏光分析

图3描述了在均匀锚定条件下测得的cellⅠ截面内归一化的透过率曲线随锚定强度的变化.我们把表面锚定强度W的值分别设为1.7× 10-7，2.5×10-7，3.3×10-7，5.0×10-7，1.0× 10-6J/m2.通过光学模拟我们发现，当W小于1.0×10-6J/m2时，液晶盒内出现了漏光，并且漏光强度随着W的减小而增大.根据第2章所给出cellⅠ的模型以及初始条件可知，初始时刻cellⅠ中的指向矢都在y-z平面内，这时把cellⅠ置于两个正交的偏振片中测得cellⅠ的透过率为零.在该初始条件下通过改变表面锚定强度让y-z平面内的指向矢通过平衡态方程随着时间进行演化，然后把平衡态的指向矢同样置于上述正交的偏振片中检测cellⅠ的透过率，如果y-z平面内的指向矢出现了自发的扭曲，即离开了y-z平面，那么在发生扭曲的区域就会有漏光被检测到，且通过计算透过率的琼斯矩阵可知扭曲角越大漏光越大.因此cellⅠ在上述不同的锚泊强度下得到的模拟结果表明:在无外场条件下，当cellⅠ的表面锚泊强度足够小时，液晶盒内的指向矢确实出现了自发的扭曲，并且扭曲角随着锚泊强度的减小而增大.在图3中我们还注意到，液晶盒右半部分的漏光稍大于左半部分的漏光.这说明:在同等锚定强度条件下，在垂面锚定区域内的指向矢的取向对外部条件的响应更敏感.

图3　不同锚定强度下cellⅠ截面内的归一化的透过率曲线Fig.3　Normalized light transmittance in the cross section of cellⅠmeasured as a function of the surface anchoring strength

在图4中我们给出了当表面锚定强度不均匀时cellⅠ的某一截面内的透过率曲线.我们把cellⅠ的基板左半部分和右半部分的锚定强度分别设为W1=1.0×10-4J/m2和W2=1.7×10-7J/m2，如图4（a）所示.模拟结果显示，截面内的透过率几乎为零，即没有漏光出现，如图4（b）所示.为了进一步说明在该条件下液晶盒内的指向矢变化，在图4（c）中我们给出了指向矢在该截面内的二维分布图.在图中指向矢用一个短棒表示，棒的长度代表着指向矢在y-z平面内的投影.从图4（c）我们观察到，在垂面锚定区域内的指向矢虽然较之初始时刻有所倾斜，但是没有发生扭曲，即指向矢位置的变化都是在y-z平面内进行的.这些结果表明当基板表面锚定强度不均匀时，垂面锚定区域内的指向矢的自发扭曲受其相邻区域锚定强度的影响强烈，当且仅当其相邻区域的锚定强度小于某一值时自发扭曲才会发生.

图4　W1=1.0×10-4J/m2且W2=1.7×10-7J/m2时的模拟结果:（a）cellⅠ的不均匀锚定示意图；（b）归一化的透过率曲线；（c）指向矢在y-z平面的分布Fig.4　Simulation results obtained as W1=1.0× 10-4J/m2and W2=1.7×10-7J/m2:（a）Schematic of cellⅠwith a nonuniform surface；（b）The normalized light transmittance；（c）The director field n（y，z）in the cross section

在基板表面不均匀锚定的基础上我们还研究了当W1∈1.7×10-7～1.0×10-6J/m2且W2= 1.0×10-4J/m2的情况.模拟结果显示，漏光不仅出现在锚定强度较弱的沿面锚定区域而且在锚定强度较强的垂面锚定区域也出现了漏光，如图5所示.此外，与图3比较我们发现在沿面锚定区域的漏光有所变大.这些结果都说明，当基板表面锚定强度不均匀时，cellⅠ内的指向矢将会产生更加严重的的自发扭曲现象.

图5　W1∈1.7×10-7～1.0×10-6J/m2且W2=1.0× 10-4J/m2时的归一化的透过率曲线Fig.5　Normalized light transmittance measured as W1∈1.7×10-7～1.0×10-6J/m2and W2=1.0×10-4J/m2

CellⅠ中的漏光本质上是由其面内指向矢的剧烈形变诱导发生扭曲形变而引起的.对比图3和图4可知，沿面锚泊强度的大小决定了整个液晶盒平衡态的指向矢取向.该结论与Atherton和Sambles的研究［6］一致，他们指出在类似于cellⅠ这种具有“展弯”结构的液晶薄盒中，只有当沿面锚泊强度小于某一值时，在特定条件下这种“展弯”结构自发的向“扭曲”结构转变.因此当cellⅠ沿面锚泊强度高于某一值时，截面内无扭曲发生.由左右两部分的指向矢的几何排布可知，在同样大小的外力矩作用下，垂直锚泊区域内的指向矢在微小的扰动下，扭曲角就可以变化很大，远大于沿面锚泊区域内指向矢扭曲角的变化.因此，在均匀锚泊条件下就会出现图3所示的垂面锚泊区域内的漏光大于沿面锚泊区域内的漏光.从图3和图5的对比可知，在沿面锚泊强度都满足较弱的情况下，由于初始时刻cellⅠ截面内指向矢存在着剧烈形变，当沿面锚泊区域的泊强度和垂面锚泊强度大小相差很大时，指向矢在这个左右锚泊强度和锚泊形式都不同的液晶盒内受到表面作用力的悬殊更大，因此诱导指向矢产生更为剧烈的扭曲形变，即表现为更严重的漏光.

4.2不同表面条件下cellⅡ中的漏光分析

图6描述了cellⅡ的截面内的透过率随锚定强度的变化.从图中我们观察到，在截面中心出现了较大的漏光，其漏光强度明显大于cellⅠ.减小基板表面的锚定强度，漏光开始增大.这表明，cellⅡ中的指向矢发生高度的自发扭曲，且扭曲角随着锚定强度的减小而增大.

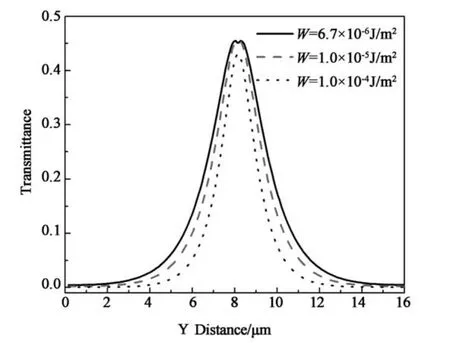
图6　cellⅡ截面内的归一化的透过率曲线随锚定强度的变化Fig.6　Normalized light transmittance in the cross section of cellⅡmeasured as a function of the surface anchoring strength

同样，我们也模拟了cellⅡ的表面锚定强度不均匀时的情形.设定cellⅡ基板右半部分的锚定强度W2=1×10-4J/m2，左半部分的锚定强度W1依次设定为2.5×10-6，3.3×10-6，5.0× 10-6，1×10-4J/m2，左右分别代表着弱锚定边界条件和强锚定边界条件，如图7（a）所示.模拟结果显示，左半部分的漏光强度明显大于右半分，且锚定强度越小漏光越严重，如图7（b）.此外我们还观察到在强锚定区域和弱锚定区域的临界处的漏光表现的较为复杂，这说明该区域的指向矢排列较为混乱，处于无序状态.

4.3自发扭曲现象的分析

对cellⅠ、cellⅡ进行模拟时我们发现，当改变夹在两基板间的液晶材料时，模拟结果大不相同.表1给出了若干液晶材料的模拟结果以及其对应的弹性常数.从表1中我们看到，有些液晶材料使得液晶盒中出现了漏光，有些却没有.通过计算机进行大量的模拟我们得出，只有弹性各向异性较大的液晶材料（L2/L1≥1，/K22/K11≤2/3）才会出现自发的扭曲现象，即才会出现漏光.

图7　不均匀锚定时cellⅡ的截面内归一化的透过率曲线Fig.7　Normalized light transmittance in the cross section of cellⅡmeasured as the surface anchoring strength is nonuniform

表1　漏光与弹性常数之间的关系Tab.1　Relationship between elastic constants and optical transmittance

这一结论与周璇等人的研究［21］是一致的，她们在单一常数近似（L2=0）下研究了具有体缺陷结构的混合排列向列相液晶盒（cellⅡ）的本征值交换.从她们的结果我们可知，指向矢的变化都平行于某一平面，即在液晶盒内没有出现自发的扭曲形变.

上述两个模型共同的特点是在初始条件下都包含体缺陷结构，为了证实漏光与缺陷结构之间的关系，我们对cellⅢ进行了研究.已知cellⅢ是一个不包含缺陷结构的混合排列向列相液晶盒，与cellⅠ、cellⅡ类似，我们通过改变cellⅢ边界条件对它进行了大量的数值模拟.模拟结果显示，无论是强锚定边界条件、弱锚定边界还是不均匀锚定边界条件，cellⅢ中都没有出现漏光，如图8所示.这意味着指向矢的自发的扭曲现象，在一定条件下，仅仅在包含体缺陷结构的液晶盒里出现.

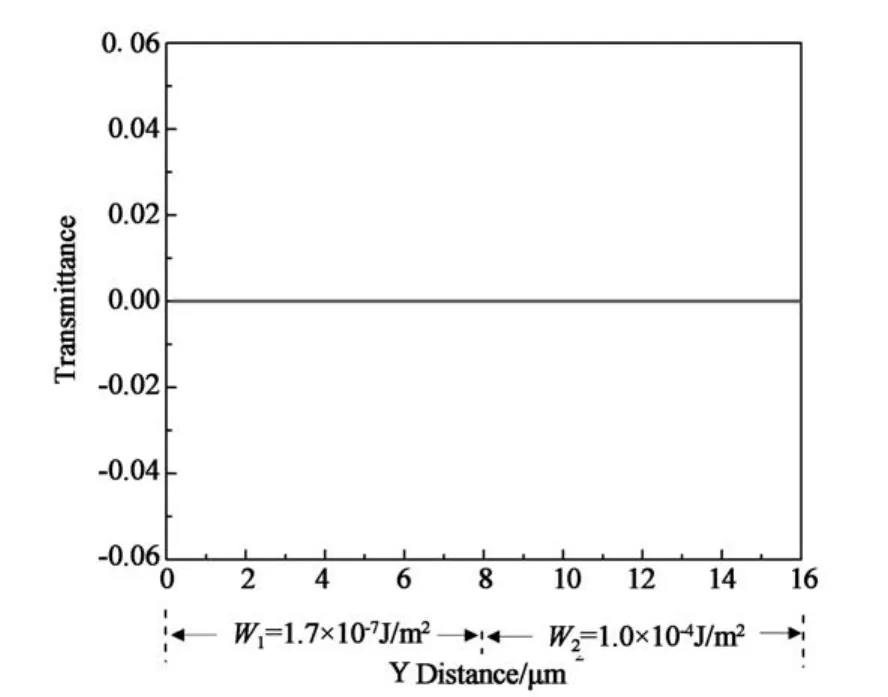
图8　不均匀锚定条件下cellⅢ截面内归一化的透过率曲线Fig.8　Normalized light transmittance in the cross section of cellⅢmeasured as the surface anchoring strength is nonuniform

我们的结论在TFT-LCD的生产过程中也得到了很好的证实.众所周知，液晶盒内指向矢的分布和受到电场和磁场作用一样，受基板表面作用的影响强烈［23-24］.然而，如果取向表面处理不当，液晶盒内将会产生各种缺陷.例如，在TFTLCD工业的取向工程阶段，在TFT基板和彩膜基板两侧需要涂覆上均匀的取向膜，然后通过摩擦的方法使得取向膜产生对液晶分子的定向能力，从而使液晶分子沿某一特定方向均匀排列.然而，当彩膜侧像素与黑矩阵之间的段差过大时，就会在段差过大区域形成摩擦弱区.摩擦弱区对液晶分子的配向能力较弱，进而各种不良现象，如漏光将会被检测到.此外，对于TFT-LCD技术的不同显示模式，摩擦强度的设置也不完全相同.摩擦强度偏低，漏光易发生，而摩擦强度偏高时，色度不均易发生.通过研究不同显示模式所需的最佳摩擦强度，能够有效降低液晶面板生产过程中不良产品的发生率.

综上所述，cellⅠ、cellⅡ在各自的边界锚定条件下，只有当夹在两基板间液晶材料的弹性常数满足L2/L1≥1（K22/K11≤2/3），即弹性各向异性较大时，指向矢才会出现自发扭曲现象，即液晶盒表现为漏光.结合上述研究我们还发现表面锚泊强度和锚泊形式对指向矢的自发扭曲影响强烈，因此我们认为本文中指向矢出现的自发扭曲现象，是在cellⅠ、cellⅡ这种具有体缺陷结构的向列相液晶薄盒中，弹性各向异性作用与表面锚泊条件共同作用的结果.

4.4介电效应和挠曲电效应对cellⅡ的影响

在TFT-LCD工业中，液晶盒在暗态出现的漏光现象可以通过施加一个较小电场来消除，这与我们的研究结果是相吻合的.我们通过给cellⅡ施加一个垂直于基板的电场来研究介电效应对自发扭曲现象的影响.模拟时我们对cellⅡ采取均匀锚定，锚定强度设定为1×10-5J/m2，施加的电场强度E∈0～0.5 V/μm.模拟结果显示，漏光强度随着电场强度的增加而减小，当电场强度达到Ec=0.163 V/μm时漏光为零，如图9（a）所示.图9（b）给出了当电场强度等于Ec时cellⅡ截面内的指向矢排布，从图中我们可以看到此时指向矢并不是都沿着电场线方向排列，这表明一定强度的电场能够克服指向矢的扭曲形变，使得漏光消失，但是不足以使指向矢全部按照电场线方向排布.继续增大电场，当E=0.362 V/μm时，液晶盒的漏光还是为零，但指向矢排布显示，几乎所有的指向矢都沿电场方向，如图9（c）所示.这一结果也再次证明了指向矢的自发扭曲现象的存在.

液晶盒内指向矢的取向受到很多外部因素的影响，接下来我研究了挠曲电效应对cellⅡ中指向矢影响.给cellⅡ施加电场时我们发现，当把挠曲电效应考虑在内时，在同等电场强度下漏光强度发生了明显的改变.图10（a）给出的是电场强度E=0.109 V/μm时cellⅡ截面内有无挠曲电效应的透过率曲线，从图中我们可以看出，在同样大小的电场强度下，挠曲电效应加剧了漏光，在一定的范围内增大电场，这种效应更加明显，如图10（b）所示.

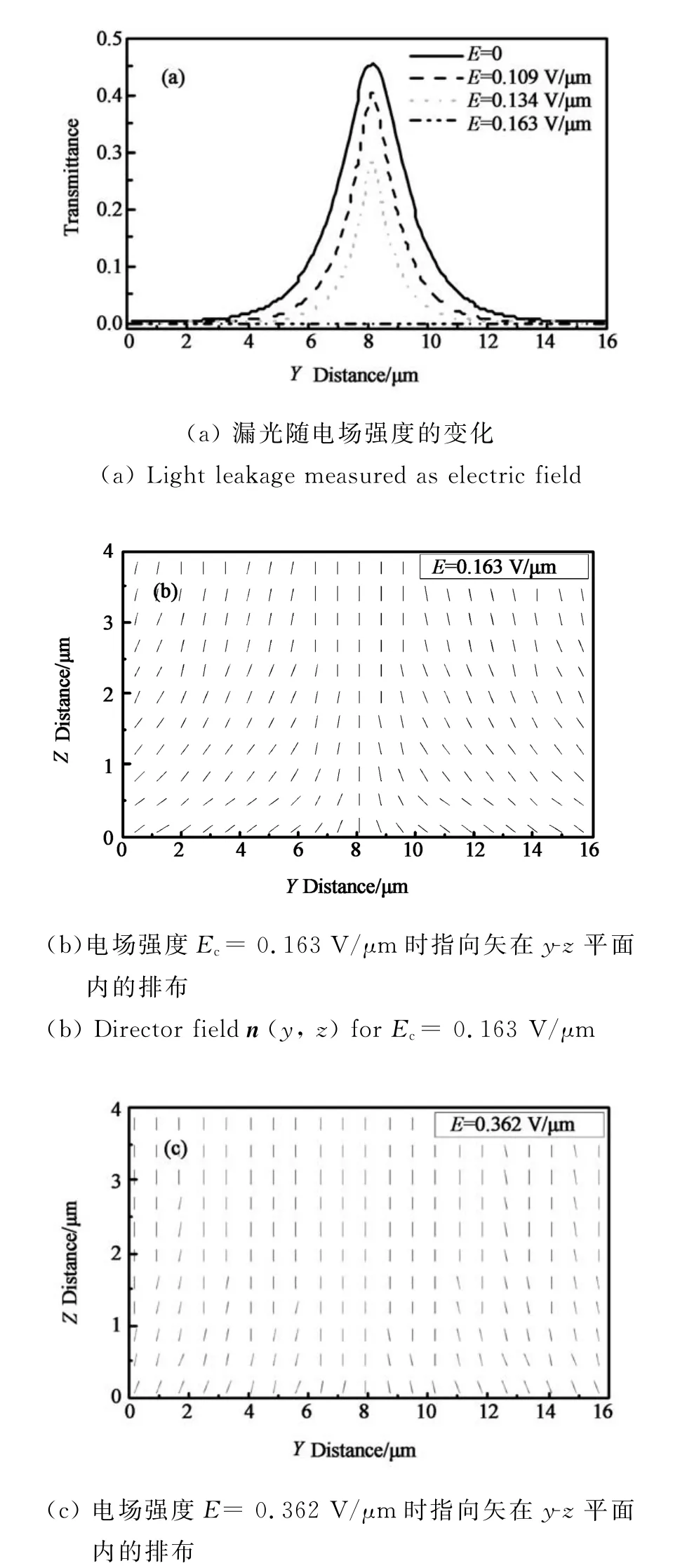
（c）Director field n（y，z）for E=0.362 V/μm图9　介电效应对cellⅡ的影响Fig.9　Influence of dielectric effect on cellⅡ

图11　较高电场强度下挠曲电效应对cellⅡ的影响Fig.11　Influence of flexoelectric effect on the light leakage in cellⅡwhen a larger electric field is applied

在考虑挠曲电效应的基础上继续增大电场强度，我们发现漏光强度随着电场强度的增加也是逐渐减小的，但是使漏光为零时所加的电场强度Ec∗=0.471 V/μm，这一数值明显高于只考虑介电效应所加的电场（Ec=0.163 V/μm），如图11所示.这些结果表明在一定的电场范围内，挠曲电效应加剧液晶盒内的漏光，即加剧了指向矢自发扭曲.

5　结 论

本文通过建立模型研究了向列相液晶弹性各向异性诱导指向矢产生的扭曲形变，这一结论在一定程度上可以解释体缺陷造成液晶盒在暗态产生漏光的现象.模拟结果显示，在无外场条件下，具有体缺陷结构的液晶盒在暗态出现的漏光是指向矢的自发扭曲形变造成的，且液晶材料的弹性各向异性（L2/L1≥1或K22/K11≤2/3）越大，自发扭曲现象越容易发生.Cell I和cell II的模拟结果都显示基板的锚泊强度越弱漏光越明显，即指向矢的扭曲角越大，并且当基板锚泊强度不均匀时漏光更严重.把cell I和cell II的模拟结果对比我们还得出，不同的体缺陷结构造成漏光的强度大小是不同的.为了研究介电效应对自发扭曲的影响，以及从多发面验证指向矢自发扭曲现象的确存在，我们以cell II为例，当给液晶盒施加一个垂直于基板方向的电场时漏光开始减小，当电场强度等于Ec时漏光消失.然而，当把挠曲电效应考虑在内时，需要施加一个更大的电场Ec∗才能使得漏光消失.

在我们的二维（y-z）模拟计算中，盒厚（z方向）取4μm，横向（y方向）线度取16μm.模拟结果表明，在这个较小的区域里可以表现为体缺陷，这种体缺陷只在偏光显微镜下才可以观测到.但事实上，当计算的横向线度扩大后，体缺陷的范围也随之扩大，对应于工艺中的可视缺陷.在TFT-LCD生产工艺中，体缺陷造成液晶盒在暗态下出现的漏光现象普遍存在，相信我们的研究能够对漏光机理解释有一定的参考价值.此外，在非显示应用领域，例如纯相位调制器件中，这种缺陷引起的扭曲形变而夹杂着振幅调制成分，由此减低了相位调制能力［25］，因此这实际上也是需要极力避免的.

［1］ Jeong J，Davidson Z S，Collings P J，et al.Chiral symmetry breaking and surface faceting in chromonic liquid crystal droplets with giant elastic anisotropy［J］.Proceedings of the National Academy of Sciences of the United States of America，2014，111（5）:1742-1747.

［2］ Williams R D.Two transitions in tangentially anchored nematic droplets［J］.Journal of Physics A:Mathematical and General，1986，19（16）:3211-3222.

［3］ Lavrentovich O D，Sergan V V.Parity-breaking phase transition in tangentially anchored nematic drops［J］.II Nuovo Cimento D，1990，12（9）:1219-1222.

［4］ Xu F，Kitzerow H S，Crooker P P.Director configurations of nematic-liquid-crystal droplets:Negative dielectric anisotropy and parallel surface anchoring［J］.Physical Review E，1994，49（4）:3061-3068.

［5］ Drzaic P S.A case of mistaken identity:spontaneous formation of twisted bipolar droplets from achiral nematic materials［J］.Liquid Crystals，1999，26（5）:623-627.

［6］ Atherton T J，Sambles J R.Orientational transition in a nematic liquid crystal at a patterned surface［J］.Physical Review E，2006，74（2）:022701.

［7］ Kléman M.Points，Lines and Walls:in Liquid Crystals，Magnetic Systems and Various Disordered Media［M］. New York:Wiley，1983.

［8］ Denniston C，Yeomans J M.Flexoelectric surface switching of bistable nematic devices［J］.Physical Review Letters，2001，87（27）:275505.

［9］ Varghese S.Patterned Alignment of Liquid Crystals by Microrubbing:A New Route Towards Wide Viewing Angle Flat Panel Displays［M］.Eindhoven:Technische Universiteit Eindhoven，2005.

［10］ 王海成，董天松，郑英花，等.TFT-LCD制程中Zara点状不良的产生与改善研究［J］.液晶与显示，2013，28（5）: 707-710.

Wang H C，Dong T S，Zheng Y H，et al.Occurrence and improvement of Zara particle in TFT-LCD cell process［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（5）:707-710.（in Chinese）

［11］ De Gennes P G，Prost J.The Physics of Liquid Crystals［M］.Oxford:Clarendon Press，1993.

［12］ Choi Y H，Kim K，Ji S，et al.Multidimensional simulation of the defect in the liquid crystal director field from Inhomogeneous patterned electrodes by using the fast Q-tensor method［J］.Journal of the Korean Physical Society，2007，51（5）:1700-1706.

［13］ Se D，Porenta T，Ravnik M，et al.Geometrical frustration of chiral ordering in cholesteric droplets［J］.Soft Matter Physics，2012，8（48）:11982-11988.

［14］ Kang W S，Joo W Y，Hur S Y，et al.Effect of the surface anchoring energy on modeling the defect in the liquid crystal director field［J］.Journal of the Korean Physical Society，2010，57（4）:752-755.

［15］ Zhou X，Zhang Z D.Dynamics of order reconstruction in nanoconfined twisted nematic cells with a topological defect.Liquid Crystals，2014，41（9）:1219-1228.

［16］ Virga E G.Variational Theories for Liquid Crystal s［M］.London:Chapman，1994.

［17］ Kleman M，Lavrentovich O D.Soft Matter Physics［M］.Berlin:Springer，2002.

［18］ Spencer T J，Care C M.Lattice Boltzmann scheme for modeling liquid-crystal dynamics:Zenithal bistable device in the presence of defect motion［J］.Physical Review E，2006，74（6）:061708.

［19］ Lombardo G，Ayeb H，Barberi R.Dynamical numerical model for nematic order reconstruction［J］.Physical Review E，2008，77（5）:051708.

［20］ Kralj S，Rosso R，Virga E G.Finite-size effects on order reconstruction around nematic defects［J］.Physical Review E，2010，81（2）:021702.

［21］ Zhou X，Zhang Z D.Dynamics of order reconstruction in a nanoconfined nematic liquid crystal with a topological defect［J］.International Journal of Molecular Sciences，2013，14（12）:24135-24153.

［22］ Guzmán O，Abbott N L，De Pablo J J.Quenched disorder in a liquid-crystal biosensor:Adsorbed nanoparticles at confining walls［J］.The Journal of Chemical Physics，2005，122（18）:184711.

［23］ Jérôme B.Surface effects and anchoring in liquid crystals［J］.Reports on Progress in Physics，1991，54（3）:391-451.

［24］ Luckhurst G R，Miyamoto T，Sugimura A，et al.The surface-induced static director distribution in thin nematic liquid crystal films:A deuterium nuclear magnetic resonance spectroscopy study［J］.The Journal of Chemical Physics，2001，114（23）:10493-10503.

［25］ 吴诗聪.液晶材料与应用［J］.现代显示，1995（2）:25-31，16. Wu S C.Materials and application of liquid crystal［J］.Advanced Display，1995（2）:25-31，16.（in Chinese）

Study of light leakage induced by the elastic anisotropy of the nematic liquid crystal

WANG Yong-chao1，ZHANG Zhi-dong2∗，ZHOU Xuan3

（School of Science，Hebei University of Technology，Tianjin 300401，China）

In the paper，we show the reasons for light leakage in the nematic liquid crystal（NLC）cells with bulk defect structure in the dark state and the influence of the anchoring conditions on it.Firstly，we give three models of NLC cells with different director distribution at the initial state.Secondly，based on the Landau-de Gennes theory，we calculate the defect dynamics of the director field and get the director distribution in the cross-section of the cells at equilibrium state.Finally，we express the director distribution in the form of light transmittance with Jones Calculus.Without applied field，the simulation results indicate that the cells with bulk defect have spontaneous twist structure under the condition of L2/L1≥1（K22/K11≤2/3），which leads to light leakage of the cells.The intensity of light leakage varies with defect structures and anchoring conditions at the boundaries.Our models can explain the light leakage in the NLC cells induced by the bulk defect in the dark state，and the results show a good agreement with the phenomena found in the process of industry manufacture.

bulk defect structure；light leakage；Landau-de Gennes theory；spontaneous distortion

O753.2

A doi:10.3788/YJYXS20153006.0949

1007-2780（2015）06-0949-11

王永超（1987-），男，河北邯郸人，硕士研究生，主要从事液晶物理等方面的研究.E-mail:929413721@qq.com

张志东（1961-），男，山东蓬莱人，教授，博士生导师，主要从事液晶物理等方面的研究.E-mail:zhidong_ zhang1961@163.com

2015-04-23；

2015-07-15.

国家自然科学基金资助项目（No.11374087；No.11447179）

Supported by National Natural Science Foundation of China（No.11374087；No.11447179）

∗通信联系人，E-mail:zhidong_zhang1961@163.com

周璇（1985-），女，河北石家庄人，博士，讲师，主要从事液晶物理等方面的研究.E-mail:zhouxuan198536@ 163.com