预测SARS疫情影响旅游人数的数学模型

郭争昊 戴依墨

摘 要：本文通過对给出的统计数据建立相应的数学模型，揭示了SARS对北京市旅游业造成的巨大影响，同时也预测了这种影响何时将会完全消除。

关键词：季节趋势;预测;数学模型;季节指数

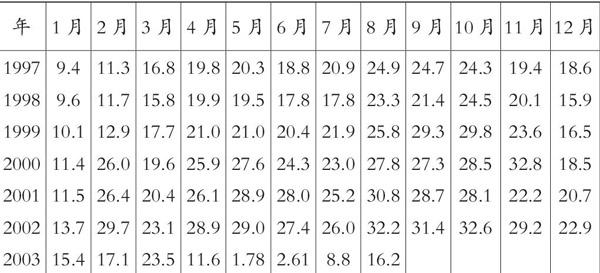
在2003年全国大学生数学建模竞赛A题第（3）小题中，要求根据北京市1997年1月至2003年8月的北京市接待的海外旅游人数，建立相应的数学模型，预测SARS疫情对北京市旅游人数造成的影响。本文根据所提供的数据的特点，采用平均趋势整理法，仅从来京旅游的海外人数的变化上，分析了SARS对北京市旅游业造成的巨大影响，同时根据给出的数据也估计出了北京市旅游业何时将彻底摆脱SARS造成的影响，使得来京旅游的海外人数将趋于正常。

一、问题的提出

根据上表给出的数据，建立相应的数学模型并进行预测。分析SARS对北京市旅游业造成的影响以及北京市的旅游业何时将趋于正常。

二、问题的分析

从表1给出的数据可以看出，1997～2002年的数据明显呈周期性的变化规律，其中周期为一年，且在不同年份的相同月份，来京旅游的海外人数是呈稳定增长趋势的。根据数据的这些特点，我们将建立平均数趋势整理法，结合1997～2002年给出的数据，预测2003年1～8月份来冰旅游的海外人数，同时跟实际人数比较，通过这几个月来京旅游的海外人数的变化，可大概得出SARS对北京市旅游业造成的影响。另外，由表1中2003年1～8月份的数据可看出，前三个月的数据基本是正常的，因此它们不受SARS的影响。从四月份开始，数据的变化明显是受SARS的影响，并且这些数据的变化规律明显呈二次曲线的变化趋势，故我们对这些数据建立它的二次曲线预测模型，来估计2003年哪个月份来京旅游的海外人数将趋于正常水平，摆脱SARS的影响。

三、模型的建立

1.趋势季节预测模型

我们使用平均数趋势整理法来建立预测模型。所谓平均数趋势整理法是先对历史资料中各年同月或同季的数据求出平均数，再利用所求出的平均数，消除其中的趋势成分，求出季节指数，最后建立趋势季节模型进行预测的方法。

以下我们用N表示年份数（即周期数），y1，y2，…yt-1，yt表示表1中1997～2003年各月份的数据，即时间序列，其中12N。

（1）求各年份同月平均数

我们以ri表示各年份第i个月的同月平均数，则有

（2）求各年份的月平均数

我们以Yj表示第j（j=1，2…，N）年的月平均数，则有

（3）建立趋势直线模型，求各趋势值

首先根据各年的月平均数，建立年趋势直线模型：T=a+bt

（t以年为单位）。可用最小二乘法来估计其中参数a，b，并取序列{Yj}的中点年作为时间原点（若N为偶数，则取年作为时间原点）。

然后我们再将此模型转化为原点年的月趋势直线模型：=a0+b0t（t以月为单位），式中a0=a+，b0=。它们分别为新原点的月趋势值和每月的增量，利用此月趋势直线模型便可求得原点年份各月份的趋势值，设分别为：1，2，…，12。

（4）求季节指数

我们先计算同月平均数与原点年该月的趋势值的比值，以fi（i=1，2，3，…，12）表示。再消除数据的随机干扰，经修正后便可得到季节指数Fi（i=1，2，…，12）。

fi=（i=1，2，…，12）

Fi=fi·θ （i=1，2，…，12. θ为修正系数）。

（5）计算预测值

首先我们用月趋势直线模型来求月份的趋势值：t=a0+b0t;其次，建立趋势季节预测模型：=（a0+b0i）Fi

（i=1，2，…，12），利用此预测模型便可求得各预测值。

2.二次抛物线预测模型

从表1给出的2003年4月份至8月份的数据可以看出，由于受到SARS的影响，它明显呈先减速后增的趋势，具有抛物线的性质，因此我们对其建立二次抛物线模型，来预测2003年8月份以后各月份海外来京旅游人数。二次抛物线预测模型为yt=a+bt+ct2，其中a，b，c为参数，t为时间变量，表示月份。同样，我们可以用最小二乘法来估计式中的参数a，b，c。

四、问题的求解

1.趋势季节预测模型的求解

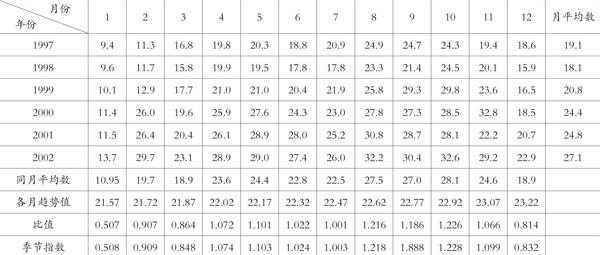
根据表1给出的数据，我们可分别求出趋势季节预测模型中的各值，结果如以下表2所示：

表2 趋势季节模型各月趋势值、季节指数计算表

月份

年份 1 2 3 4 5 6 7 8 9 10 11 12 月平均数

1997 9.4 11.3 16.8 19.8 20.3 18.8 20.9 24.9 24.7 24.3 19.4 18.6 19.1

1998 9.6 11.7 15.8 19.9 19.5 17.8 17.8 23.3 21.4 24.5 20.1 15.9 18.1

1999 10.1 12.9 17.7 21.0 21.0 20.4 21.9 25.8 29.3 29.8 23.6 16.5 20.8

2000 11.4 26.0 19.6 25.9 27.6 24.3 23.0 27.8 27.3 28.5 32.8 18.5 24.4

2001 11.5 26.4 20.4 26.1 28.9 28.0 25.2 30.8 28.7 28.1 22.2 20.7 24.8

2002 13.7 29.7 23.1 28.9 29.0 27.4 26.0 32.2 30.4 32.6 29.2 22.9 27.1

同月平均数 10.95 19.7 18.9 23.6 24.4 22.8 22.5 27.5 27.0 28.1 24.6 18.9

各月趋势值 21.57 21.72 21.87 22.02 22.17 22.32 22.47 22.62 22.77 22.92 23.07 23.22

比值 0.507 0.907 0.864 1.072 1.101 1.022 1.001 1.216 1.186 1.226 1.066 0.814

季节指数 0.508 0.909 0.848 1.074 1.103 1.024 1.003 1.218 1.888 1.228 1.099 0.832

根据最小二乘法，且分别取1997、1998、1999、2000、2001、2002的时间t分别为-3、-2、-1、0、1、2，则可算得参数a=22.39，b=1.82，故我们可得年趋势直线模型为T=22.39+1.82t。进一步我们可得：a0=22.47，b0=0.15。因此我们可得原点年（2000年）的月趋势直线模型为：=22.47+0.15t。此模型以7月为原点，则t分别取-6、-5、-4、-3、-2、-1、0、1、2、3、4、5，便可得原点年1—12月的月趋势值（如表2所示）。

另外，我们可出公式fi=（i=1，2，…，12）可得各比值（见表2）。

一般来讲，12个月的季节指数的平均数应为1，12个月的季节指数之和应为12，但是表2中的比值之和却为：Σ fi=11.982，因此，我们需要对它们进行修正。为此，先求修正系数θ。

再用此系数分别乘以表2中的各比值，即为各季节指数Fi（如表2所示）。

最后，根据趋势季节预测模型，我们可预测得到2003年各月份的海外来京旅游人数分别为

1=（22.47+0.15×30）×0.508=13.7

2=（22.47+0.15×31）×0.909=24.7

3=（22.47+0.15×32）×0.848=23.1

4=（22.47+0.15×33）×1.074=29.4

5=（22.47+0.15×34）×1.103=30.4

6=（22.47+0.15×35）×1.024=28.4

7=（22.47+0.15×36）×1.003=28.0

8=（22.47+0.15×37）×1.218=34.1

9=（22.47+0.15×38）×1.888=53.2

10=（22.47+0.15×39）×1.228=34.8

11=（22.47+0.15×40）×1.099=31.8

12=（22.47+0.15×41）×0.832=23.8

通过分析比较实际的数据与预测的数据，尤其是4月份至8月份的数据，我们可以看到，由于受到SARS的影响，实际上2003年4月份至8月份的数据分别为：11.6、1.87、2.61、8.8、16.2，而按到正常情况下，它应当和我们预测的数据差不多，这几个月预测的数据分别为：29.4、30.4、28.4、28.0、34.1。因此我们得到如下结论：由于SARS的影响，这几个月来京旅游的海外人数呈现急剧下降的态势，特别是5、6、7三个月，可见SARS对北京市旅游业的影响是非常严重的。另外，根据1至3月份的预测数据可以看出，用季节趋势预测模型去刻画表1中的数据还是比较精确的。

2.二次抛物线预测模型的求解

根据表1给出的2003年各月的数据，使用最小二乘法，可以估计出二次抛物线预测模型yt=a+bt+ct2中的各参数分别为：a=27.0259，b=-6.7477，c=0.6064。因此可得以上模型为yt=27.0529-6.7477t+0.6064t2

我们分别令t=9，10，11，12，则可得到2003年9、10、11、12這四个月份的预测数据为：y9=15.4，y10=20.2，y11=26.2，y12=33.4。

从这些数据可以看出，这四个月来京旅游的海外人数呈现恢复性增长，到11月份已基本上恢复正常了，这与事实也是比较相符的。

以上给出的两个模型虽然只是针对北京市的情况，但它具有一般性，对于其他地方也具有较好的应用价值。

参考文献：

[1]暴奉贤，陈宏立.经济预测与决策方法[M].广州：暨南大学出版社，1991.

[2]雷功炎.数学模型讲义[M].北京：北京大学出版社，1999.

[3]姜启源.数学模型[M].北京：高等教育出版社，1993.

[4]郭永发.线性回归模型的QR参数估计[J].数学的实践与认识，2002（1）：173-174。

[5]华伯泉，经济预测的统计方法[M].北京：中国统计出版社，1988.