基于复合单叶双曲面的广义Stewart平台全局动态各向同性优化设计*
田体先 姜洪洲 何景峰 佟志忠 黄其涛
(哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨150001)
完全动态各向同性的并联机构意味着其在各自由度方向上的加速度特性完全一致,具有最佳的控制精度与动态响应,是从设计角度解决传统并联机构因本征强耦合特性导致的控制性能变差问题的根本途径.
Asada[1-2]首次对并联机构动态特性进行了量化分析;随后Yoshikawa[3]提出了动力学操作度椭球(DME)的概念,描述了机构在局部位姿下其惯量特性与执行器末端加速度特性的关系,并给出了动力学操作度系数(DMI)的定义,其物理意义为动力学操作度椭球的长短轴比,反映了并联机构的动态各向同性;Ma 等[4-5]则进一步提出了动态条件数(DCI)指标并将其应用于结构优化设计中.
Jiang 等[6]提出了一种基于模态频率的动态各向同性指标,并证明了传统Stewart 并联机构实现完全各向同性时要求负载转动惯量满足条件:Ixx=Iyy且Izz=4Ixx.实质上,Izz=4Ixx这一约束条件在实际中很难满足.
为打破传统Stewart 并联机构对负载的苛刻约束条件,学者们提出了多种广义Stewart 并联机构.如McInroy 等[7-8]提出了一类局部运动各向同性的镜像对称冗余Stewart 并联机构的设计方法;He等[9]对旋转对称冗余Stewart 并联机构的动态各向同性进行了研究;而Jiang 等[10-11]则基于单叶双曲面重新描述Stewart 并联机构,并采用复合单叶双曲面形式构造出具有完全动态各向同性的广义Stewart 并联机构;佟志忠等[12-14]进一步深入分析了基于单叶双曲面广义Stewart 并联机构的力各向同性、解耦中心等问题,将其应用于隔振、精密跟瞄及六维力传感器领域.
然而,上述动态各向同性指标及其设计方法只适用于振动台或隔振平台等具有局部小工作空间的并联机构,而对于飞行模拟器等运动范围较大的并联机构而言,则需考虑全局特性.
截至目前,针对并联机构全局特性的文献尚不多见,目前学者们主要采用的方法为将局部性能指标在全域工作空间积分并取均值[15],这类方法计算量大且结果受工作空间网格划分的影响.
文中通过分析并联机构局部频率特性的导数信息,给出了一种新的全局动态各向同性指标,结合基于复合单叶双曲面的广义Stewart 平台,给出了具有局部动态各向同性且全局特性最优的结构设计方法.
1 广义Stewart 平台结构描述
1.1 定义
由上、下平台及6 条支腿组成并联机构,各支腿逆时针按照奇偶序号分为两组,奇序号支腿相同,偶序号支腿相同,分别位于上、下平台的两组同心圆内,且满足旋转对称性质,如图1 所示,称这类并联机构为广义Stewart 并联机构.

图1 广义Stewart 平台定义Fig.1 Definition of generalized Stewart platform
1.2 数学描述
由广义Stewart 并联机构的定义可知,6 条支腿按奇偶序号分为两组:a1b1、a3b3、a5b5为一组,a2b2、a4b4、a6b6为一组.从数学角度而言,两组支腿实质上位于复合单叶双曲面S1和S2中,如图2 所示.

图2 位于复合单叶双曲面上的广义Stewart 并联机构型式Fig.2 Structure type of generalized Stewart parallel manipulator lying on a pair of circular hyperboloid
复合单叶双曲面S1和S2则通过线列Г1和Г2分别逆时针依次旋转120°生成,二者的数学表述为

式中,r1、r2为单叶双曲面喉部半径,a1z、a2z为单叶双曲面中心距,c1、c2为单叶双曲面特征系数.
根据式(1)及(2),给出广义Stewart 并联机构的中位雅可比矩阵Jlx数学表述形式:

式中:α 为线列Г1和Г2绕z 轴的转动角度,0≤α≤30°;

1.3 局部完全动态各向同性解析约束条件
将并联机构各支腿看作刚度为kl的线性弹簧,则工作空间刚度阵Kt可表述为

式中,kl为支腿刚度.
当负载质心与并联机构惯性坐标系{M}的原点重合时,惯性参数阵可表述为

式中:I 为三阶单位阵;m 为负载质量;Ic为负载惯量阵,Ic=diag(Ixx,Iyy,Izz).
结合式(4)与(5),得到系统动态特性特征矩阵:

当系统动态特性特征矩阵GT为单位阵的倍数时,并联机构实现完全动态各向同性,此时并联机构各个自由度方向的加速度特性完全一致,具有最佳的动态特性.
对于标准Stewart 并联机构而言,实现完全动态各向同性的约束条件为Izz=4Ixx,这一约束条件在实际中无法满足[10].
文中采用复合单叶双曲面描述的广义Stewart并联机构,消除了对负载的约束条件.定义喉部半径比为

满足完全动态各向同性的复合单叶双曲面的解析参数约束条件如下.
(1)当n=1 时:

(2)当n≠1 时:

选择喉部半径比n 及角度α,则根据式(8)或式(9)得到一族具有相同雅可比阵、在中位具有完全动态各向同性的并联机构.
2 全局动态各向同性
为进一步设计得到并联机构的具体参数,如图3所示,首先以解耦中心O 为对称中心,对复合单叶双曲面分别偏置距离d,得到基准平面P1、P2,在此基础上,进一步将基准平面P1、P2向z 轴正向平移高度h,截取平面P1′和P2′作为上平台平面,固定支腿长度L,则构造出位于复合单叶双曲面上的具有工程可行性的广义Stewart 并联机构参数集合.

图3 广义Stewart 并联机构构造方式Fig.3 Construction of generalized Stewart parallel manipulator
可见,满足局部完全动态各向同性的广义Stewart并联机构结构参数为一个解集,而这些并联机构在全域工作空间内的特性并不相同,本节给出衡量并联机构全局频率变化特性的全局动态各向同性指标.
对考虑位姿x=[x y z Φ θ ψ]的系统动态特性特征矩阵GT(x)求其特征值,有

式中:ωi为GT(x)的第i 阶特征值,ui为GT(x)的第i 阶特征向量.
将式(10)两边对位姿变量xj(j =1,2…,6)偏微分,有

基于式(12),文中给出可表征并联机构全局特性的模态灵敏度矩阵H,表述为
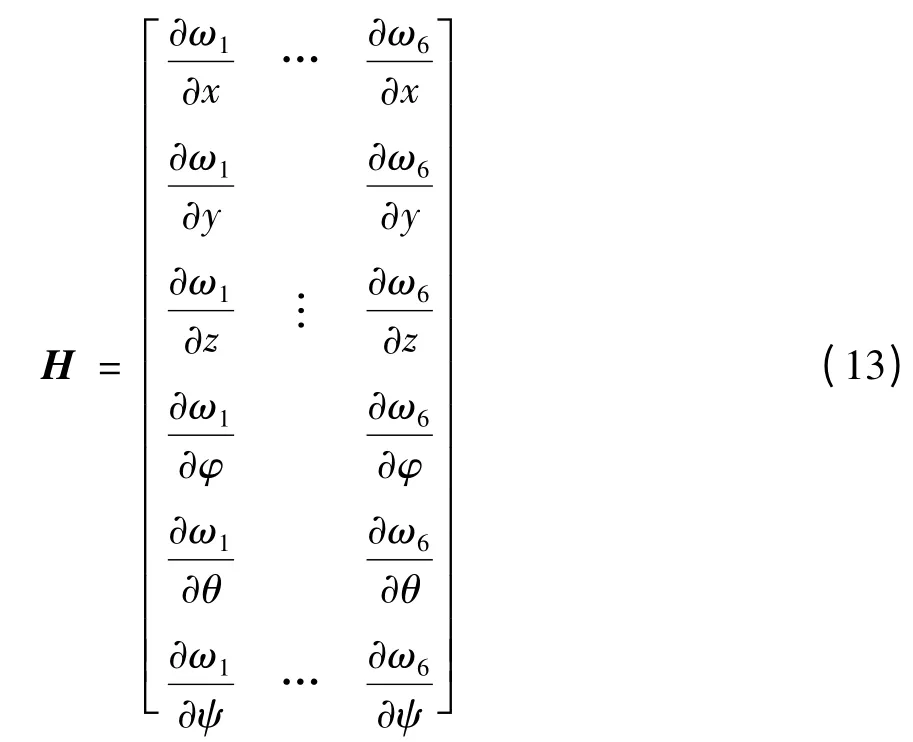
由于式(13)只适用于单特征值的情形,文中采用摄动法消除并联机构中位时由于重特征值造成的影响,式(13)中各元素求解方法为

式中,Δ 为相应自由度上的摄动量,如

H 即为全局动态各向同性评价矩阵,矩阵各元素值越小,表明频率对位姿的变化越不敏感,全局动态各向同性越好.
基于矩阵H,文中得到了一种新的评价并联机构全局动态各向同性指标(GDI),表述为

式中,hi,j为权重系数,
全局各向同性指标量化了并联机构在全域工作空间内各阶模态频率的变化情况.ηg越小,模态频率的变化率越小,全局空间内的各向同性特性越好,同时意味着全局空间内远离奇异的程度越好.
3 优化设计
基于全局动态各向同性指标,可对并联机构的全域频率特性进行量化分析,进而从满足局部完全动态各向同性的广义Stewart 并联机构参数解集中找到具有最优全局动态各向同性的结构参数.
3.1 优化问题描述
基于复合单叶双曲面描述的广义Stewart 并联机构的结构参数包括:r1、r2、a1z、a2z、ka1、ka2、kc1、kc2、α、d、h、L.实际工程设计中,支腿长度L 为设计值,以α、d、h 作为优化变量,以局部完全动态各向同性作为约束条件,则其他参数可唯一确定.
以全局动态各向同性为优化目标的优化设计问题描述如下:
目标函数:全局动态各向同性指标ηg最小.
优化变量:[α d h].
约束条件:局部完全动态各向同性.
优化设计的基本步骤如下:
(1)构型选择,即n=1 或n≠1;
当n=1 时,并联机构上平台平面P′1和P′2重合,此时d=0.当n≠1 时,优化变量多一个,机构灵活性更大.
(2)给定支腿长度L;
(3)以式(8)或式(9)为约束条件,寻找函数ηg(α,d,h)的最小值;
(4)校验结构可实现性,若不满足,则跳转到步骤(1).
3.2 设计实例
给定负载质量m = 4 300 kg,转动惯量Ic=diag(4100,4100,6700)kg·m2. 按3.1 节的描述进行优化设计,给出n=1 及n=0 时的两组优化结果.
(1)喉部半径比n=1 时
以α、h 作为优化变量,与全局各向同性指标GDI 的三维曲线如图4 所示.

图4 参数α、h 与GDI 的关系Fig.4 Relationship between parameters α,h and GDI
优化得到的并联机构结构如图5 所示.其中,上平台为两组蓝色同心圆所围成的环形区域,下平台为两组红色同心圆所围成的环形区域. 具体结构几何参数见表1.

表1 n=1 时优化的结构几何参数Table 1 Optimized structural geometric parameters when n=1

图5 n=1 时的优化结构Fig.5 Optimized structure when n=1
(2)喉部半径比n=0 时
以α、d 作为优化变量,与全局各向同性指标GDI 的三维曲线如图6 所示.
优化得到的并联机构结构如图7 所示.可以看到,对于喉部半径比n =0 的机构而言,其上平台或下平台并非一个平面,两组蓝色圆均为上平台,而两组红色圆均为下平台.具体结构参数见表2.

图6 参数α、d 与GDI 的关系Fig.6 Relationship between parameters α,d and GDI

图7 n=0 时的优化结构Fig.7 Optimized structure when n=0

表2 n=0 时优化的结构几何参数Table 2 Optimized structural geometric parameters when n=0
对比图5 与7,尽管二者结构型式相差很大,但其中位雅可比阵完全相同,且均远离奇异对比图4 与6 可以看到,尽管其喉部半径比n=0 的并联机构型式复杂,但具有更为良好的全局各向同性.
4 结语
文中通过对基于模态分析的系统动态特性特征矩阵特征值灵敏度进行分析,建立了表征并联机构全域工作空间内频率变化特性的全局各向同性指标.以该指标为优化目标,局部完全动态各向同性解析条件为约束,实现了具有最佳完全动态各向同性的广义Stewart 并联机构结构优化.该方法为大运动范围Stewart 并联机构如飞行模拟器等的结构设计提供了一个有效的工具.
[1]Asada H.A geometrical representation of manipulator dynamics and its application to arm design[J]. Journal of Dynamic Systems,Measurement,and Control,1983,105(3):131-135.
[2]Asada H.Dynamic analysis and design of robot manipulators using Inertia Ellipsoids [C]∥Proceedings of 1984 IEEE International Conference on Robotics and Automation.Atlanta:IEEE,1984:94-102.
[3]Yoshikawa T.Dynamic manipulability of robot manipulators[J].Journal of Robotic Systems,1985,2(1):113-124.
[4]Ma O,Angeles J.The concept of dynamic isotropy and its applications to inverse kinematics and trajectory planning[C]∥Proceedings of the IEEE International Conference on Robotics and Automation.Cincinnati:IEEE,1990:481-486.
[5]Ma O,Angeles J. Optimum design of manipulator under dynamic isotropy condition [C]∥Proceedings of the IEEE International Conference on Robotics and Automation.Atlanta:IEEE,1993:470-475.
[6]Jiang H Z,He J F,Tong Z Z. Characteristics analysis of joint space inverse mass matrix for the optimal design of a 6-DOF parallel manipulator[J].Mechanism and Machine Theory,2010,45(5):722-739.
[7]McInroy J E,O’Brien J F,Allais A A,.Designing dynamics and control of isotropic Gough-Stewart micromanipulators[C]∥Proceedings of 2013 IEEE International Conference on Robotics and Automation (ICRA). Karlsruhe:IEEE,2013:1458-1464.
[8]Allais A A,McInroy J E,O’Brien J F.Locally decoupled micromanipulation using an even number of parallel force actuators[J]. IEEE Transactions on Robotics,2012,28(6):1323-1334.
[9]He J F,Jiang H Z,Tong Z Z,et al.Study on dynamic isotropy of a class of symmetric spatial parallel mechanisms with actuation redundancy [J]. J Vibration Control,2012,18(8):1156-1164.
[10]Jiang H Z,Tong Z Z,He J F.Dynamic isotropy design of a class of Gough-Stewart parallel manipulators lying on a circular hyperboloid of one sheet [J]. Mechanism and Machine Theory,2011,46(3):358-374.
[11]Jiang H Z,He J F,Tong Z Z,et al.Dynamic isotropic design for modified Gough-Stewart platforms lying on a pair of circular hyperboloids [J]. Mechanism and Machine Theory,2011,46(9):1301-1305.
[12]佟志忠,姜洪洲,何景峰,等.基于广义Stewart 平台的精密跟瞄机构动态各向同性优化设计[J]. 宇航学报,2011,32(5):1019-1025.Tong Zhi-zhong,Jiang Hong-zhou,He Jing-feng,et al.Optimal design of generalized stewart parallel manipulator based precise tracking-pointing platform with dynamic isotropy [J]. Journal of Astronautics,2011,32(5):1019-1025.
[13]佟志忠,姜洪洲,何景峰,等.基于单叶双曲面的标准Stewart 并联结构六维力传感器各向同性优化设计[J].航空学报,2011,32(12):2327-2334.Tong Zhi-zhong,Jiang Hong-zhou,He Jing-feng,et al .Optimal design of isotropy performance of six-dimensional force sensor based on standard Stewart parallel structure lying on a circular hyperboloid of one sheet [J].Acta Aeronautica et Astronautica Sinica,2011,32(12):2327-2334.
[14]佟志忠,段广仁,何景峰,等.基于加速度各向同性的空间光学仪器主动隔振Stewart 平台设计[J]. 振动与冲击,2012,31(2):109-114.Tong Zhi-zhong,Duan Guang-ren,He Jing-feng,et al.Optimal design of an acceleration isotropy-based active vibration isolation Stewart platform for spaceborne optical instrument[J].Journal of Vibration and Shock,2012,31(2):109-114.
[15]Gosselin C M,Angeles J.A global performance index for the kinematic optimization of robotic manipulators [J]. ASME Journal of Mechanical Design,1991,113(3):220-226.

