薄壁箱梁的挠曲剪滞分析
卢重阳
(兰州工业学院 土木工程学院,甘肃 兰州 730050)
薄壁箱梁的挠曲剪滞分析
卢重阳
(兰州工业学院 土木工程学院,甘肃 兰州 730050)
剪力滞效应是箱形截面梁普遍存在的一种现象,不仅影响箱梁的应力分布还影响其挠度,致使不同桥型在各种荷载作用下其挠度增加。现详细论述剪滞效应对不同桥型挠度的影响,并总结剪力滞对箱梁挠度的影响程度。
薄壁箱梁;剪力滞;挠曲
0 引言
箱形截面梁由于具有自重轻、跨越能力大、抗扭刚度大及施工方便等优点,备受桥梁工程师的青睐,而剪力滞效应是箱形截面梁普遍存在的一种现象,如不考虑此影响,将会使结构的实际应力被低估[1]。而剪滞效应不但影响箱梁的应力分布,还会影响梁的挠度,致使不同桥型在各种荷载作用下其最大挠度的增加程度不同。
1 基本方程的建立
箱梁在任意竖向分布荷载q(z)作用下发生挠曲变形时(见图1),其纵向位移表达式为:
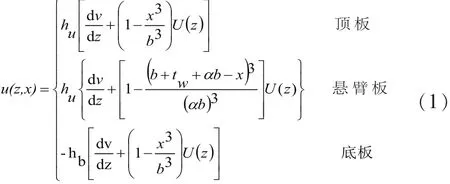
式中:U(z)---翼板最大位移差函数;
v(z) ---箱梁截面的竖向挠度。
箱梁的总势能为:

式中:V、U---外力势能及应变能;
E、G---弹性模量及剪切模量;
I、Is---箱梁截面的惯性矩及翼板对截面形心轴的惯性矩。

图1 箱梁的坐标系、荷载及横截面图
根据δⅡ=0,可得微分方程及边界条件如下:
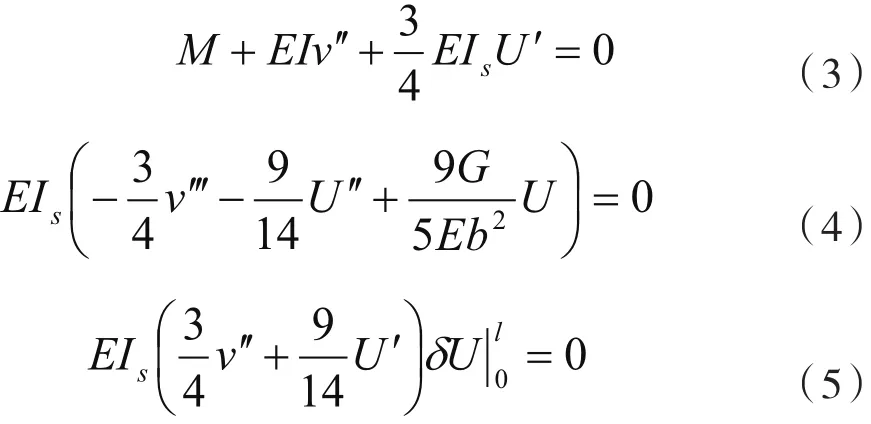
由式(3)、式(4)可得:

其中:

2 几种桥型的挠度公式
2.1 简支箱梁在集中荷载作用下(见图2)
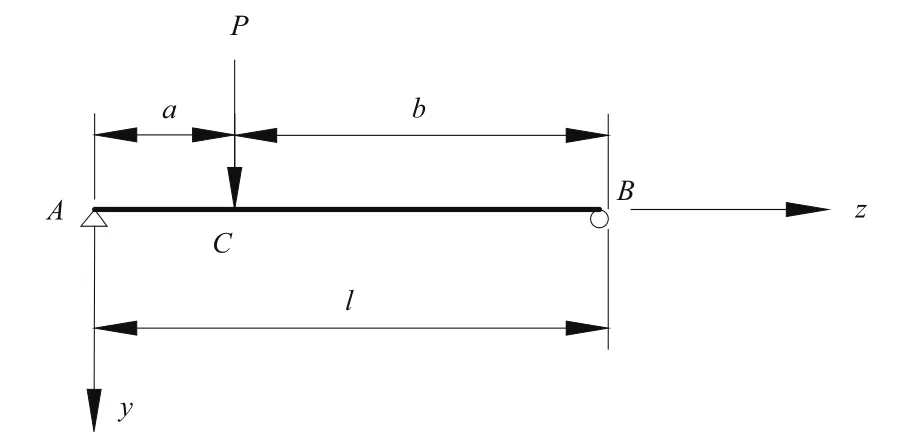
图2 简支箱梁承受集中荷载示意图
弯矩和剪力方程为:
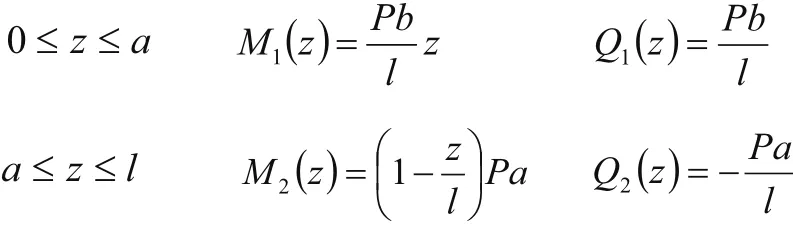

只考虑集中荷载作用在跨中则有:
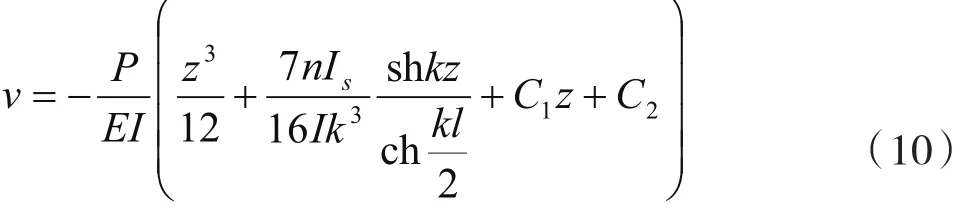

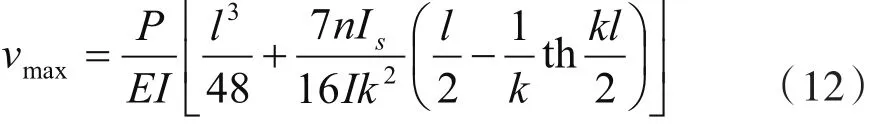
2.2 简支箱梁在均布荷载作用下(见图3)

图3 简支箱梁承受均布荷载示意图
弯矩和剪力方程为:


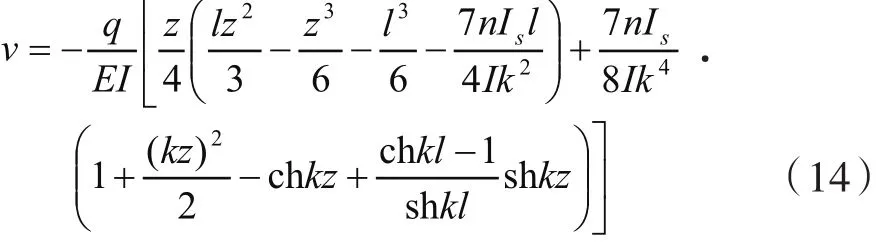
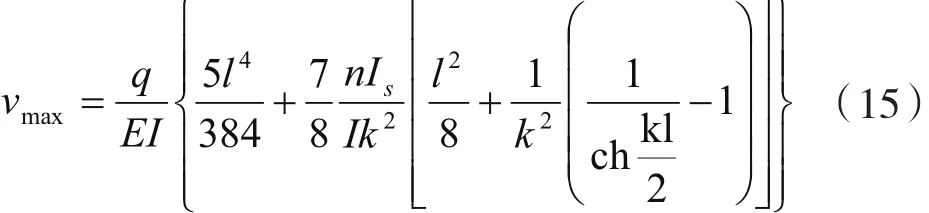
2.3 悬臂箱梁自由端作用集中荷载(见图4)
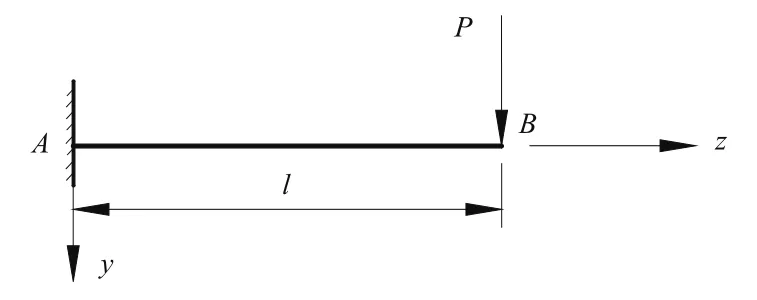
图4 悬臂箱梁自由端作用-集中荷载示意图
弯矩和剪力方程为:
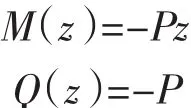

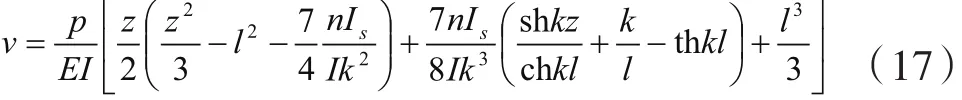
当z=0时,最大挠度为:

2.4 悬臂箱梁在均布荷载作用下(见图5)
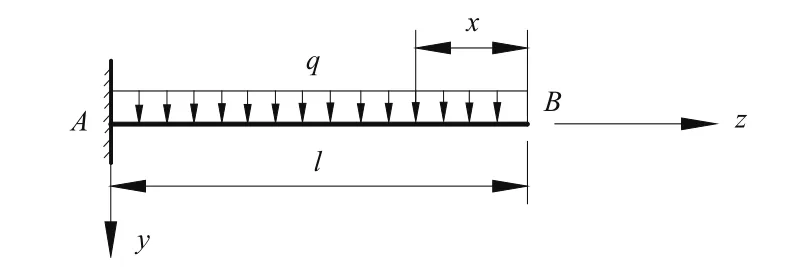
图5 悬臂箱梁承受均布荷载示意图
弯矩和剪力方程为:

由边界条件
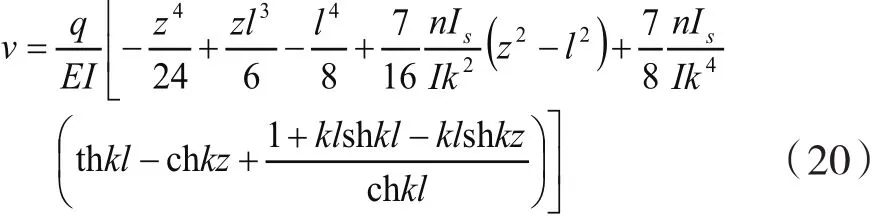
最大挠度为:

3 算例
取文献[2]算例,箱梁l=60 m,Is/I=0.821,b=7.9 m, k=0.262,n=3.55l。由式(12)、(15)、(18)、(21)求得简支箱梁在集中荷载作用、均布荷载作用下最大挠度分别为:

悬臂箱梁在自由端集中荷载作用下和均布荷载作用下的最大挠度分别为:

由算例得出,考虑剪滞效应时,不同类型的薄壁箱梁在集中荷载和均布荷载作用下,最大挠度值都有不同程度的提高,简支箱梁在集中荷载作用下提高10.8%,在均布荷载作用下提高9.6%,悬臂箱梁自由端作用集中荷载时提高2.9%,在均布荷载作用下提高了3.6%,简支箱梁的最大挠度值增加最为显著 。由此得出剪滞效应不仅影响箱梁的应力分布还影响其挠度,且对挠度的影响比较显著,特别是大肋间距的简支梁桥[3],因此在设计薄壁箱梁是必须考虑剪滞效应对其挠度的影响。
[1] 罗旗帜,吴幼明.薄壁箱梁剪力滞理论的评述和展望[J].佛山科学技术学院学报,2001,(3):29-33.
[2] Evans H R,Ahmad M K H,Kristek V Shear lag in comPosite box girders of complex cross-sections. J. Constr. SteelRes,1993.
[3] 张元海,李乔.斜交箱梁桥剪滞效应的有限元分析[J].西南交通大学学报,2005,40(1):64-68.
U441+.5
B
1009-7716(2015)07-0066-03
2015-04-10
卢重阳(1980-),女,甘肃通渭人,副教授,从事教学工作。

