同塔四回不对称参数线路的相模变换

刘 琦 邰能灵 范春菊 于仲安 尚



同塔四回不对称参数线路的相模变换

刘 琦1邰能灵1范春菊1于仲安2尚1

（1. 上海交通大学电子信息与电气工程学院 上海 200240 2. 江西理工大学电气工程与自动化学院 赣州 341000）

同塔多回线中线路自阻抗的不对称增大了矩阵解耦的难度，参数不对称同塔四回线为电力系统的故障分析带来新的挑战。在对以往同塔多回线相模变换进行大量研究的基础上，根据同塔四回线相模变换的特点，提出了基于线相解耦法的相模变换与基于相线解耦法的相模变换，这两种解耦方式对参数不对称的同塔四回线进行解耦。从变换矩阵的特性探索了这两种相模变换所表现的物理意义，从数学角度分析了相模变换解耦过程的顺序性与可逆性，并且从相模变换的数学方程与物理意义讨论了相模变换的适用性，对相模变换矩阵进行了推广应用。仿真结果表明此方法能够较准确地计算线路的故障电流，并能很好地适用于不对称线路的故障分析。

同塔四回线 不对称线路 相模变换 解耦 矩阵变换

0 引言

同塔四回线是指在同一杆塔上架设四回线路，该四回线路可以是同一电压等级，也可是不同的电压等级。采用同塔四回线输电可有效地解决输电走廊面临的土地资源问题，并能显著提升输电容量[1]。随着节约型社会的不断推进和电网建设的突飞猛进，输电走廊的征地和建设费用所占比例越来越高，电网输电线路的传输功率也越来越大，国内同塔四回线杆塔的比例也日益提升，自阻抗参数不完全一致的同塔四回线的比例也逐渐提升。

电力系统发生故障时，系统内的耦合将影响故障电流的计算，不利于电力系统的故障分析。输电线路的相模变换（如对称分量法）能消去系统网络方程中的互感耦合，得到不含耦合的序分量或模分量，便于故障电流的计算，序分量电压、电流的故障特性使系统的故障分析更方便，并在电力系统继电保护中得到了广泛应用[2-11]。文献[12]提出了一种新的单回线相模变换矩阵，使单一模量能反映所有类型的故障。文献[13]提出了一种同塔多回线的序网参数修正方法，为同塔多回线的序网结构和故障短路电流计算奠定了基础。

随着同塔多回线的不断发展，同塔双回线的故障分析与相模变换已得到广泛的研究与应用，但同塔四回线的研究相对较少。文献[14]提出了一种基于正序、负序和零序的复合序网法，解决同塔双回线的短路故障。文献[15-17]采用相分量法分析双回线的故障。文献[18]提出了多端口理论解决线路中的多重故障，但简单故障时的计算较为复杂繁琐。文献[19]提出了一种跨电压等级四回线的故障计算方法，但零序分量未完全解耦，序网图绘制复杂，在实际应用中存在一定的局限性。

本文针对线路自阻抗矩阵不一致的同塔四回线模型（简称不对称同塔四回线），对传统的对称同塔多回线的相模变换进行了研究，探索了不对称同塔四回线的相模变换方式，并研究了基于线相解耦的相模变换与基于相线解耦的相模变换两种解耦方式的区别及优缺点。分别从物理意义和数学分析的角度阐释了相模变换的本质与充要性，根据相模变换的数学方程与物理意义提出相模变换的适用性，对相模变换矩阵进行了推广，并利用文中所述的解耦方法进行了故障短路电流的仿真。

1 不对称参数的四回线的线路参数特点

12序分量法对线间耦合阻抗的考虑过于理想化[20-22]，在实际模型中，因为空间位置与线间距离的差异，各回线间的互阻抗是不可能完全相等的。文献[23]采用更接近实际的线路阻抗模型解决上述问题，提出12序分量扩展法实现了对称同塔四回线的阻抗解耦与故障分析，并进行了数学验证。不对称同塔四回线路则是在接近实际线路阻抗模型的基础上，考虑线路自阻抗不完全一致的情况，因此阻抗矩阵的解耦更为复杂与繁琐。

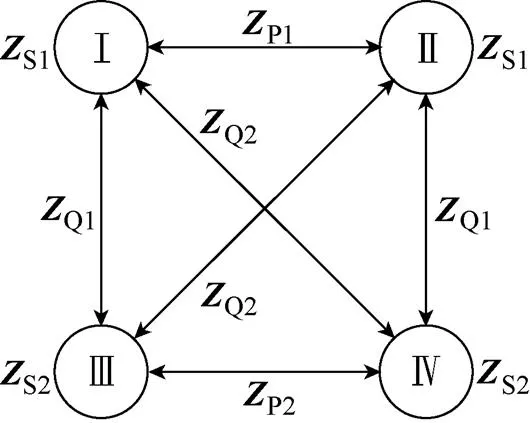
图1 不对称参数同塔四回线的线间互阻抗

由于杆塔结构存在一定的左右对称性，考虑线路互阻抗与空间距离的关系，图1结构中存在以下关系：Ⅰ、Ⅲ回线间的线间互阻抗和Ⅱ、Ⅳ回线间的线间互阻抗相同；Ⅰ、Ⅳ回线间的线间互阻抗和Ⅱ、Ⅲ回线间的线间互阻抗相同；而Ⅰ、Ⅱ回线之间的线间互阻抗和Ⅲ、Ⅳ回线间的线间互阻抗不同。

不对称参数的同塔四回线电压-电流关系为

式中

12序分量扩展法虽然能够完全解耦对称同塔四回线，但对式（1）进行相似变换后得到的矩阵并非对角矩阵，解耦后阻抗矩阵的非对角线元素中，存在3类非零元素，其表达式为

2 不对称同塔四回线的解耦方法

2.1 基于线相解耦法的解耦方法

传统的双回线和四回线相模变换均遵循先进行线间解耦，再进行相间解耦的方式实现多回线路的相模变换，这里统称为线相解耦法。对于不对称四回线路，也遵循同样原则，即使用线相解耦法进行解耦。对式（1），选择相似矩阵

式中

线路结构确定，可得到式（1）所示的线路矩阵，再计算式（3）的不对称补偿系数。引入不对称补偿系数，可较好地反映线路的空间结构特点。若线路完全对称，则和的值为1；线路的不对称度越大，和值越远离1。

式（1）经过式（2）的相似变换后，得到分块对角矩阵，此时各回线分量已完成了线间解耦，解耦后的各回线均与其他回线相互独立，因此只需再完成回线内三相线路的解耦，即可完成不对称四回线的完全解耦。变换后的分块对角阵中，每一个小的分块矩阵均与单回线的阻抗矩阵类似，因此可以选择相似矩阵

式中，矩阵表示单回三相线路解耦所使用的各种变换矩阵，如对称分量法的复数矩阵、卡伦鲍尔变换矩阵或克拉克变换矩阵等。经变换后得到

式中

线相解耦法采用先进行线间解耦，再进行相间解耦的方式实现不对称参数四回线的解耦。其中，线间解耦矩阵为矩阵，相间解耦矩阵为矩阵。由式（2）可知，线间解耦变换矩阵的物理意义没有12序分量扩展法明显。在不对称线路中，Ⅰ回线的每个分量与Ⅲ回线和Ⅵ回线中的所有分量均相关，Ⅱ、Ⅲ、Ⅳ回线也有类似情况。若将矩阵等效为对称分量法的复数矩阵，则经过相模变换后得到的各序分量中，Ⅰ回线的每个分量与Ⅲ回线和Ⅳ回线中的零序分量有关，而与Ⅲ回线和Ⅳ回线的正序分量和负序分量无关。由此可见，先进行线间解耦再进行相间解耦，会使矩阵物理意义变弱，且必须依赖矩阵才能更好地解释变换矩阵所表达的物理意义，降低了线间解耦变换和相间解耦变换物理意义的独立性。

2.2 基于相线解耦法的解耦

2.1节提出用线相解耦法进行不对称参数四回线的解耦，考虑变换矩阵的特殊性及矩阵乘法原则，可调整相模变换中解耦的顺序。即先进行各回线内的相间解耦，再进行线间解耦，从解耦角度同样能够实现四回线的完全解耦[24]，这里称之为相线解耦法。

对式（1）选择相似矩阵，其表达式如式（4）所示。变换后的阻抗矩阵为

至此已完成各回线内部的相间解耦，再进行线间解耦，即可实现矩阵的完全解耦。由式（6）可知，线间耦合量均集中在零序分量中，正序分量与负序分量已实现完全解耦。

由式（4）和式（7）可得到相线解耦法的综合变换式

由式（8）和式（9）可知，相线解耦法采用的变换矩阵与12序分量扩展法的变换矩阵略有区别，即矩阵中线间互感位置所对应的元素不同。在12序分量扩展法的变换矩阵中，3阶分块方阵都是由单位矩阵构成，而相线解耦法则由矩阵构成，非零元素只集中在第一列且与线路的不对称补偿系数直接相关。

对于正序分量和负序分量，e分量和f分量分别为Ⅰ回线与Ⅱ回线的同向分量与反向分量，g分量和h分量分别为Ⅲ回线和Ⅳ回线的同向分量和反向分量。零序分量与每回线均相关，e分量为四回线线间的同向分量，f分量、g分量和h分量为四回线线间的环流量。

相线解耦法分解得到的零序分量如图2所示。其中，e分量为四回线组间的同分量；f、g和h分量为四回线组间的环流量；和为不对称补偿系数。若将同塔四回线进行两两分组，即Ⅰ回线与Ⅱ回线一组，Ⅲ回线与Ⅳ回线为一组，则e分量为组间同向且组内同向的分量组，f分量为组间同向但组内反向的分量组，g分量为组间反向但组内同向的分量组，h分量为组间反向且组内反向的分量组。当线路对称时，可得到，此时同向分量和环流量将与12序分量扩展法所对应的同向分量与环流量基本一致。

图2 基于相线解耦法的零序电流

3 解耦的数学分析与推广

3.1 解耦法的数学解释

对式（1）相模变换过程的本质就是对阻抗矩阵进行对角化的过程。由数学分析可知，式（1）中的阻抗矩阵一定能对角化，因此必存在相似矩阵，使得阻抗矩阵实现对角化。其中，对角矩阵与原阻抗矩阵的特征值相对应，相似矩阵由特征值对应的特征向量组成。

结合同塔多回线的阻抗矩阵的特性，可将阻抗矩阵视为分块矩阵，因此可将矩阵对角化的过程划分为两个阶段。考虑变换的可逆性与顺序性，可得

式中，矩阵用于实现分块矩阵内部的对角化，即物理意义上的相间解耦，其表现形式如式（4）所示；矩阵与矩阵用于实现分块矩阵间的对角化，即物理意义上的线间解耦矩阵，且矩阵为前置线间解耦矩阵，为后置线间解耦矩阵。因此，线相解耦法和相线解耦法解耦得到的序分量是一致的，但因前置线间解耦矩阵与后置线间解耦矩阵的不同，导致两种方法解耦过程的物理意义发生变化。两个线间解耦矩阵之间的关系为

对于同塔四回对称线路，矩阵可分解为由3阶单位矩阵构成的12阶分块矩阵，考虑单位矩阵的特性，因此有

对于对称线路，先进行线间解耦再进行相间解耦，与先进行相间解耦再进行线间解耦，在数学计算与物理意义上不存在任何区别，即线相解耦法和相线解耦法所使用的数学方程与所表达的物理意义完全一致。但对不对称线路，由于线间解耦矩阵存在不对称补偿系数，因此不能推导出式（12），从而导致前置解耦矩阵和后置解耦矩阵是两个不同的矩阵。

3.2 相模变换的推广

考虑相线解耦法的线间解耦矩阵物理意义较明显，因此在相线解耦法的基础上，引入广义矩阵，用表示。可分解为3个矩阵。即

式中，矩阵为单回线内部解耦因子，是由单回线变换矩阵构成的对角阵；矩阵为线间对称解耦因子；矩阵为线间不对称修正因子，用于线间不对称部分的解耦和修正分解后各序存在的耦合。由此可将对称线路的变换矩阵与不对称线路的变换矩阵统一表示。对于对称线路，不需进行不对称修正，故为单位阵，在计算中不影响结果，在进行对称线路计算时可被忽略。同时，由于矩阵的特性，矩阵与矩阵的位置可互换，即可通过线相解耦法和相线解耦法解耦，且两者的、矩阵均相同。

当四回线均不对称，线间将不存在任何线间对称，所以矩阵将退化为单位阵，由矩阵负责完成线间的不对称解耦，实现变换矩阵表现形式的统一。在解耦时，矩阵将四回线的阻抗矩阵变换成如式（6）的形式，然后提取出未解耦的零序分量，利用矩阵对4阶矩阵进行再次解耦。一方面使得解耦的过程具有良好的物理意义，同时简化不对称参数四回线的解耦难度，从12阶矩阵转变为4阶矩阵的解耦。

线路的对称与否由线路的表现形式决定，因此可认为对称线路是不对称线路的一种特殊情况，并对线路按照不对称线路的方式进行解耦，则矩阵将退化为单位矩阵，线间耦合因子全部由矩阵负责解耦。此时可得到不对称补偿系数，零序分量的解耦方式与12序分量扩展法一致，验证了对称线路是不对称线路的一种特殊情况。因此，相线解耦法不仅能够解耦不对称参数的同塔四回线，同时还可解耦对称同塔四回线，实现对称同塔四回线解耦的一个矩阵为

式中，矩阵1的表达式如式（9）所示，1表示第1列为1，其余元素为0的三阶矩阵。

4 计算与仿真验证

4.1 故障计算

通过前文可计算适于不对称线路的解耦矩阵，在发生线路故障时，可得到故障时的边界条件，利用的逆矩阵可将边界条件转换为各解耦后的序分量之间的约束关系，从而构建序分量间的综合序网图。如A相接地（IAG）故障，其故障边界条件经过的逆矩阵变换后得到

（16）

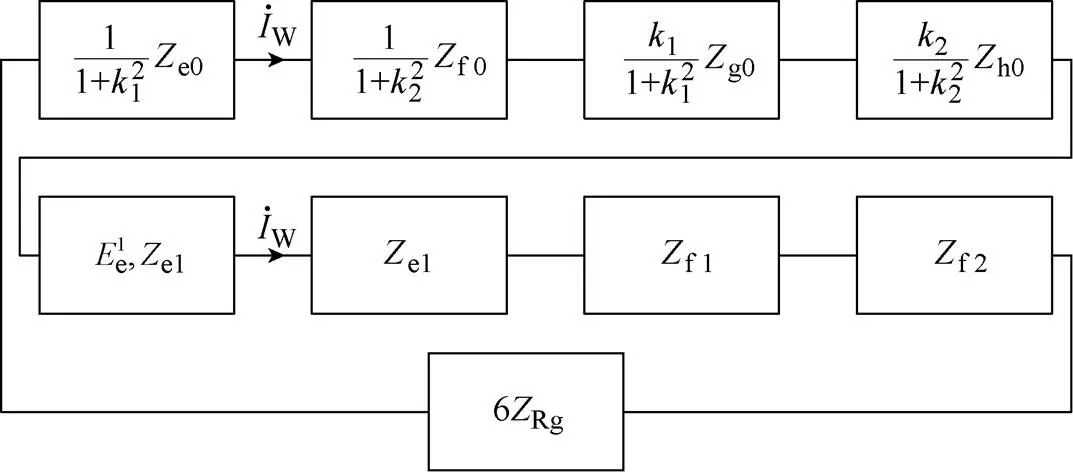
图3 IAG故障时的综合序网

4.2 系统模型与参数设定

本文采用PSCAD/EMTDC对不对称解耦方法进行仿真与验证。仿真系统结构如图4所示，线路模型采用总长为100km的TLine模型。TLine模型使用Frequency Dependent（Phase）Model进行仿真，线路换相方式采用仅回线内换相，各回线间不换相，其他参数参见附录。杆塔空间结构、导线模型等如附图所示，PSCAD计算的单位线路阻抗矩阵见附表1和附表2所示。

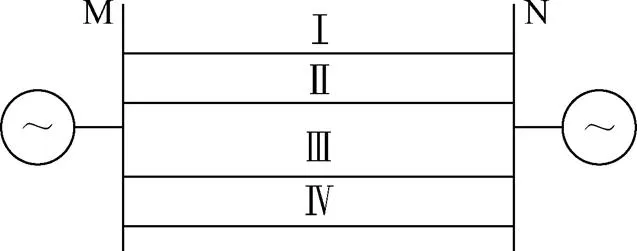
图4 不对称参数同塔四回线路仿真模型

附图 PSCAD输电线路杆塔模型

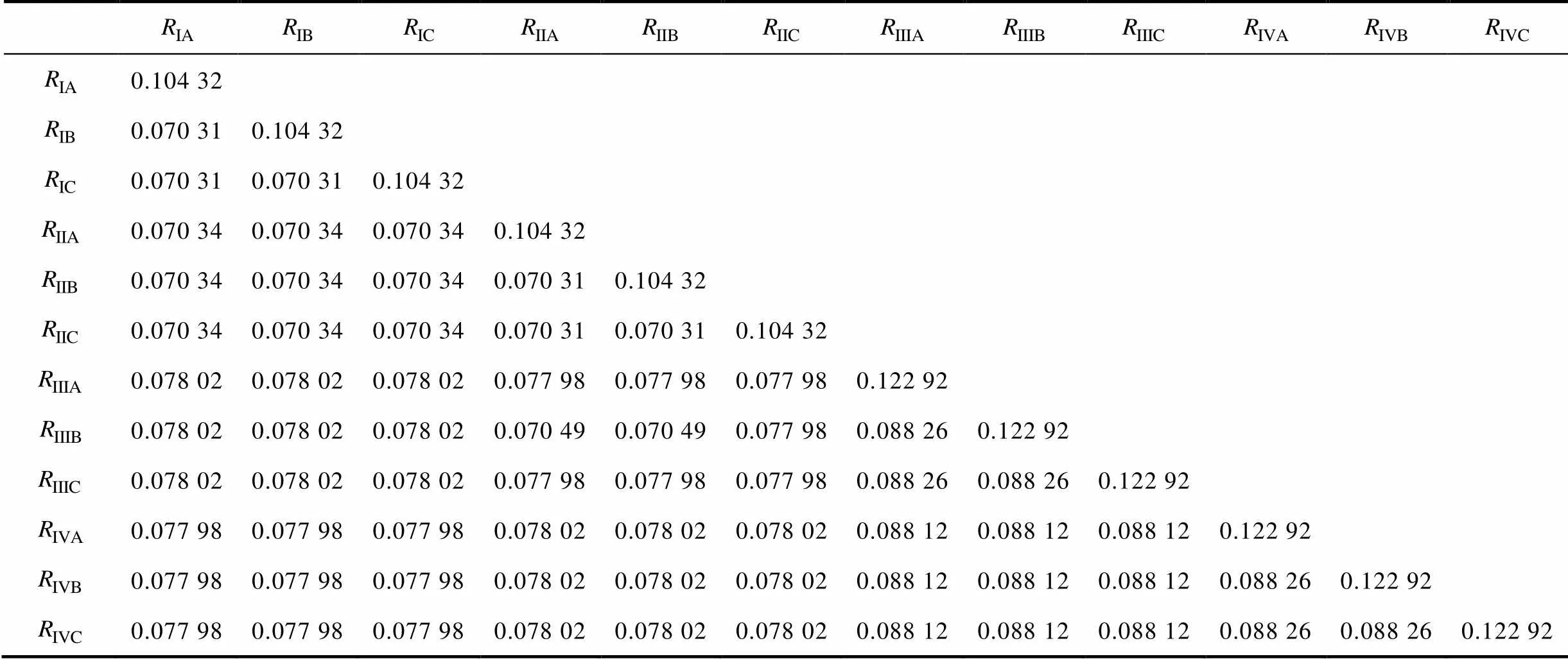
附表1 输电线路阻抗矩阵电阻部分

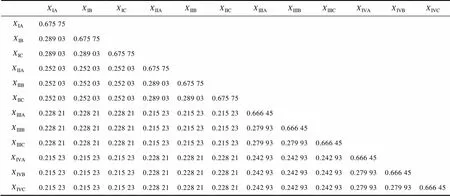
附表2 输电线路阻抗矩阵感抗部分

4.3 仿真结果

在传统多回线路故障仿真与计算中，当线路发生短路故障时，均认为故障为金属性接地。在实际短路故障中，故障点处存在一定的过渡电阻，该过渡电阻将影响故障综合序网的结构与序电流的大小，即影响故障时的各相故障电流。仿真时考虑了不同类型故障在不同接地电阻情况下的特点，金属性故障的仿真结果见表1，有过渡电阻的故障仿真结果见表2。其中，罗马字母Ⅰ、Ⅱ表示故障回线，英文字母A、B、C表示故障相，英文字母G表示接地故障，如IBCG表示Ⅰ回线B、C两相接地故障。

表1 不同故障类型下的故障电流（Rg=0）

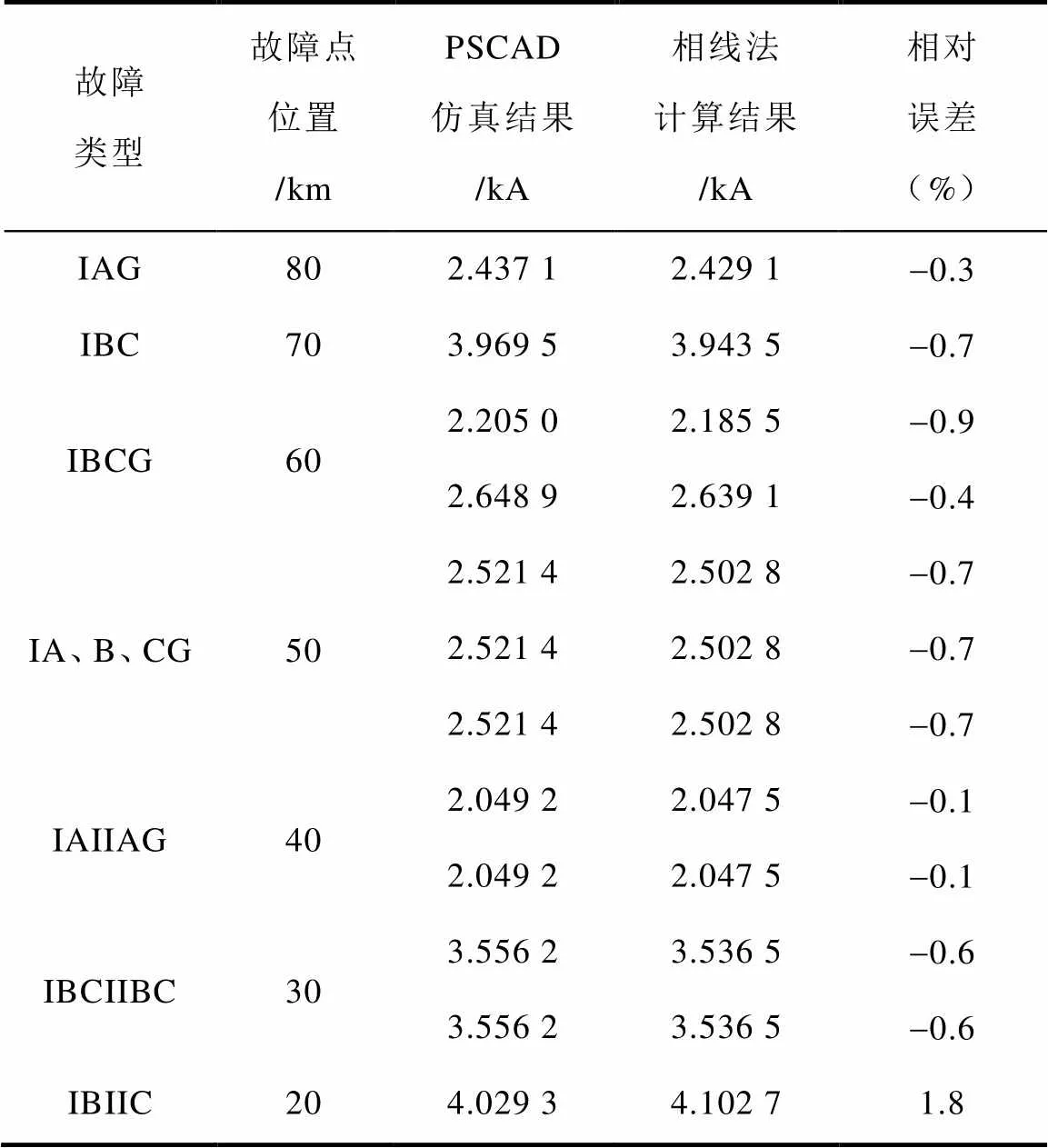
表2 不同故障类型下的故障电流（Rg=50W）

由表1可知，基于相线解耦法的不对称参数四回线解耦方法能够较好地实现故障分析，计算误差较小。由表2可知，相线解耦法具有较好的故障过渡电阻处理能力，且故障时的相对误差与金属性短路故障的误差接近。因此，相线解耦法能够很好地用于不对称线路的故障分析。

5 结论

本文基于不对称同塔四回线的数学模型，对不对称同塔四回线的相模变换进行了研究，提出了相线解耦法的分解方式，推导了数学变换的充要条件，从数学和物理意义上阐述了相模变换的意义，对变换矩阵进行了推广，并研究了相模变换的适用性。分析表明，相线解耦法不仅能够完全解耦不对称线路，还适用于对称线路的故障分析，能够简化运算，便于分析。仿真结果表明，基于相线解耦法的不对称参数四回线解耦方法不仅能够较准确地计算线路故障时的电流，而且很好地用于不对称线路的故障分析。

附 录

PSCAD的杆塔结构如附图所示。其中，C1～C3为第一回线；C4～C6为第二回线；C7～C9为第三回线；C10～C12为第四回线。杆塔的空间整个结构与文章的图2对应。杆塔的导线使用PSCAD自带的Chukar模型进行仿真。通过设置杆塔的空间参数生成线路的阻抗矩阵，PSCAD输出的线路阻抗矩阵见附表1和附表2。

PSCAD电源阻抗部分使用集中参数模型，电源电压为230kV，M端电源的正序阻抗为j12W、零序阻抗为0.349 05+j19.996 95W，N端电源的正序阻抗为j10W、零序阻抗为0.261 79+j14.997 72W。

由附表1和附表2可知，Ⅰ、Ⅲ回线间的线间互阻抗和Ⅱ、Ⅳ回线间的线间互阻抗相同，而Ⅰ、Ⅱ回线间的线间互阻抗和Ⅲ、Ⅳ回线间的线间互阻抗不同，与文章中图2的互阻抗的关系相对应，进而构建出如式（1）的矩阵表达式。此时各回线内互阻抗的不对称度接近5%，有些达到10%。

[1] 张嘉旻, 葛荣良. 同塔多回输电技术特点及其应用分析[J]. 华东电力, 2005, 33(7): 23-26.

Zhang Jiamin, Ge Rongliang. Features and application of power transmission technology of multi-circuit lines on the same tower[J]. East China Electric Power, 2005, 33(7): 23-26.

[2] 王向平, 徐磊, 张晓秋. 同塔并架四回线中线路保护的适应性[J]. 电力系统自动化, 2007, 31(24): 80-85.

Wang Xiangping, Xu Lei, Zhang Xiaoqiu. Line protection feature study on adaptation to four-circuit transmission lines on a same tower[J]. Automation of Electric Power Systems, 2007, 31(24): 80-85.

[3] 龚震东, 范春菊, 郁惟镛, 等. 一种基于六序网图的同杆双回线故障测距算法[J]. 电力系统自动化, 2007, 31(17): 58-60, 82.

Gong Zhendong, Fan Chunju, Yu Weiyong, et al. A new fault allocation algorithm for parallel transmission line based on six sequence network[J]. Automation of Electric Power Systems, 2007, 31(17): 58-60, 82.

[4] 徐鹏, 王钢, 李海锋, 等. 基于环流量的同杆四回输电线路故障选线[J]. 电力系统保护与控制, 2011, 39(3): 78-83, 118.

Xu Peng, Wang Gang, Li Haifeng, et al. Fault line selection for four-parallel lines on same tower based on circulation currents[J]. Power System Protection and Control, 2011, 39(3): 78-83, 118.

[5] 邓孟华, 范春菊, 宗明, 等. 基于环流分量的同杆四回线选相方法[J]. 电力系统保护与控制, 2012, 40(1): 138-144.

Deng Menghua, Fan Chunju, Zong Ming, et al. New faulted phase selecting method for four transmission lines on the same tower based on loop flow component[J]. Power System Protection and Control, 2012, 40(1): 138-144.

[6] 龚震东, 范春菊, 田羽. 一种适合于同杆4回线的故障测距方法[J]. 电力系统自动化, 2007, 31(23): 70-73.

Gong Zhendong, Fan Chunju, Tian Yu. A fault location algorithm suitable for jointed four transmission lines[J]. Automation of Electric Power Systems, 2007, 31(23): 70-73.

[7] 张琦兵, 邰能灵. 基于六序电流分量的同塔多回线横差保护选线元件[J]. 电力系统自动化, 2011, 35(14): 93-97.

Zhang Qibin, Tai Nengling. Fault line selection component of transverse differential protection based on six-sequence current component for multi-circuit transmission line on same tower[J]. Automation of Electric Power Systems, 2011, 35(14): 93-97.

[8] 林军. 超高压同杆双回线多重故障的计算[J]. 中国电机工程学报, 2010, 30(13): 89-93.

Lin Jun. Multi-fault calculation of EHV double circuits transmission lines[J]. Proceedings of the CSEE, 2010, 30(13): 89-93.

[9] Xu Peng, Wang Gang, Li Haifeng, et al. A new method for fault line selection of four-parallel transmission lines[C]. Asia-Pacific Power and Energy Engineering Conference, 2010: 1-4.

[10] Xu Peng, Wang Gang, Li Haifeng, et al. A short-circuit fault calculation scheme for four-parallel transmission lines[C]. Asia-Pacific Power and Energy Engineering Conference, 2010: 1-4.

[11] 葛耀中. 新型继电保护与故障测距原理与技术[M]. 西安: 西安交通大学出版社, 1996.

[12] 宋国兵, 李森, 康小宁, 等. 一种新相模变换矩阵[J]. 电力系统自动化, 2007, 31(14): 57-60.

Song Guobing, Li Sen, Kang Xiaoning, et al. A novel phase-mode transformation matrix[J]. Automation of Electric Power Systems, 2007, 31(14): 57-60.

[13] 舒巧俊, 范春菊. 同杆2回和4回线路中序网参数修正方法研究[J]. 现代电力, 2010, 27(1): 45-48.

Shu Qiaojun, Fan Chunju. Parameters’modification method to two- and four-jointed parallel lines[J]. Modern Electric Power, 2010, 27(1): 45-48.

[14] 李博通, 李永丽, 李洪波, 等. 同杆双回线短路故障复合序网分析法[J]. 电力系统自动化, 2010, 34(9): 53-58.

Li Botong, Li Yongli, Li Hongbo, et al. New method for short-circuit fault analysis on double-circuit transmission line based on interconnection of sequence networks[J]. Automation of Electric Power Systems, 2010, 34(9): 53-58.

[15] 傅旭, 王锡凡. 同杆双回线跨线短路故障计算的等值双端电源相分量法[J]. 电力系统自动化, 2004, 28(7): 54-57.

Fu Xu, Wang Xifan. An equivalent two source phase domain of interline fault analysis for the double circuit line on the same pole[J]. Automation of Electric Power Systems, 2004, 28(7): 54-57.

[16] 傅旭, 王锡凡. 同杆双回线断相故障计算的解耦相分量法[J]. 电力系统自动化, 2004, 28(6): 41-44.

Fu Xu, Wang Xifan. A decoupling phase domain method to calculate open conductor faults in the double circuit line on the same pole[J]. Automation of Electric Power Systems, 2004, 28(6): 41-44.

[17] 王安宁, 陈青, 周占平, 等. 改进的相分量法求解同杆双回线故障新算法[J]. 电力系统自动化, 2009, 33(13): 58-62, 77.

Wang Anning, Chen Qing, Zhou Zhanping, et al. An improved phase component method for calculating faults on the double-circuit transmission line on the same tower[J]. Automation of Electric Power Systems, 2009, 33(13): 58-62, 77.

[18] 陈青, 徐文远. 同杆双回线故障分析新方法研究[J]. 中国电机工程学报, 2005, 25(20): 68-71.

Chen Qing, Xu Wenyuan. Research on fault analysis of double circuit lines on the same tower[J]. Proceedings of the CSEE, 2005, 25(20): 68-71.

[19] 刘玲, 范春菊. 基于六序分量法的跨电压等级的同塔四回线的故障计算[J]. 电力系统保护与控制, 2010, 38(9): 6-11.

Liu Ling, Fan Chunju. Fault calculation for joint four transmission lines of different voltage grades on the same tower based on six-sequence-component method[J]. Power System Protection and Control, 2010, 38(9): 6-11.

[20] 田羽, 范春菊, 龚震东. 同杆4回线12序分量法[J]. 电力系统自动化, 2007, 31(21): 35-39, 105.

Tian Yu, Fan Chunju, Gong Zhendong. Twelve sequence component method of four-parallel lines on same towers[J]. Automation of Electric Power Systems, 2007, 31(21): 35-39, 105.

[21] Su Zhipeng, Wang Pingping, Yang Zheng, et al. Method for parameter decoupling for four-circuit transmission lines on the same tower[C]. Asia-Pacific Power and Energy Engineering Conference, 2012: 1-4.

[22] Fan Chunju, Liu Ling, Tian Yu. A fault-location method for 12-phase transmission lines based on

twelve-sequence-component method[J]. IEEE Trans- actions on Power Delivery, 2011, 26(1): 135-142.

[23] 张琦兵, 邰能灵, 袁成, 等. 同塔四回输电线的相模变换[J]. 中国电机工程学报, 2009, 29(34): 57-62.

Zhang Qibing, Tai Nengling, Yuan Cheng, et al. Phase-mode transformation of four-parallel lines on the same tower[J]. Proceedings of the CSEE, 2009, 29(34): 57-62.

[24] 李博通, 李永丽, 陈莉, 等. 同塔四回线参数解耦及故障分析方法[J]. 电力系统保护与控制, 2010, 38(19): 1-9.

Li Botong, Li Yongli, Chen Li, et al. Method for parameter decoupling and fault analysis of four- circuit transmission lines on the same tower[J]. Power System Protection and Control, 2010, 38(19): 1-9.

Phase-Mode Transformation of Asymmetry-Parameter Four-Parallel Lines on the Same Tower

11121

（1. Shanghai Jiaotong University Shanghai 200240 China 2. Jiangxi University of Science and Technology Ganzhou 341000 China）

Due to the asymmetrical self-impedance of the multi-circuit lines, it becomes much more difficult to decouple the network equation and brings new challenges for fault analysis with four-parallel lines on the same tower. According to the studies of existing phase-mode transformation and the characteristics of the four-parallel-line phase-mode transformation, two new decoupling methods are proposed to decouple the asymmetrical impedance matrix. One is to decouple the matrix with the original decouple steps, while the other uses the contrary order. The physical meanings of the two phase-mode transformations are discussed according to the characteristics of the transformation matrix, and their mathematical calculation is deduced to explore the sequentiality and the reversibility of the decouple steps. Applicability of the phase-mode transformations is explained according to their physical meanings and mathematical equations, and the phase-mode transformation form is also generalized. The simulation results indicate that the new method is suitable for the fault analysis involved in four-parallel lines with asymmetrical self-impedance.

Four-parallel lines on the same tower, asymmetry-parameter lines, phase-mode transformation, decoupling, matrix transformation

TM773

刘 琦 男，1987年生，博士研究生，主要研究方向为电力系统保护与控制。

邰能灵 男，1972年生，教授，博士生导师，主要从事电力系统保护与控制及电力市场方向的教学与研究工作。

2013-09-10 改稿日期 2014-01-14

国家自然科学基金资助项目（51177066、51377104）。