数学建模的教学方法与策略研究

董君

（吉林省经济管理干部学院 ，吉林　长春　130012）

数学建模的教学方法与策略研究

董君

（吉林省经济管理干部学院 ，吉林长春130012）

开展数学建模方法的教学的能够拓展、丰富和深化数学建模的教学理论，也能够更好地指导数学建模在教学中的实践。在具体的教学中应该注意对数学建模的教学策略，主要包括：注重数学建模方法的各环节之间的联系；对于数学建模方法采取分阶段的教学方式；加强数学建模方法的多元化表征；将数学建模方法与现实问题联系交叉。

数学建模；教学方法；教学策略

随着社会的不断发展和进步，我国的教育事业也快速的繁荣起来。数学建模的教学方法越来越受到大学老师的重视和青睐。在高校中，数学建模的教学具有十分重要的意义，但是也存在着较多的问题。要解决这些问题需要从老师和学生两方面共同抓起。需要对数学建模的教学方式与策略进行分析研究，

1　数学建模的概述和意义

简单来说，数学建模就是指数学模型的建立过程，主要是通过利用数学方式和方法解决实际问题。具体的过程是首先将所考察和研究的现实问题转化为数学问题，建立相应的数学模型，然后求解提炼的数学模型解决所探究的现实问题［1］。

如果对数学建模方法没有一个系统的掌握，只知道一些碎片化的零散知识，在遇到现实问题时就难以用数学建模的方式去解决和处理。虽然数学建模的方式和模式不存在固定、统一和通用，但在一定程度上，还是存在一些具有普遍适应性的基本方法。

2　数学建模的教学方法与策略

2.1注重数学建模方法的各环节之间的联系

2.1.1重视数学建模方法的步骤

首先，需要对于数学建模方法的各个步骤的含义、作用、特点以及各个步骤之间的关系及相互作用做出详细的讲解和阐述，并解释其各步骤应该注意的问题［2］。然后从数学建模的方法层次对情境感知、问题理解、做出假设、提炼模型、求解模型、解释应用和模型评价等各个步骤展开分析。在教学时，注意讲解步骤时需要在同一个现实问题的背景之中。使学生能够系统的掌握数学模型方法的建立，为以后模仿建模与独立建模提供可循的依据和原则指导。

2.1.2重视普遍适应性的数学建模方法

普遍适应的数学建模方法，对于解决现实问题是最简单可行的，也是在解决现实问题时，应该首先采用的办法。包括关系分析、理论分析、数据分析、图形分析、平衡原理法等数学建模基本方法。

2.1.3注意其他相关的数学建模方法

包括极限建模、微分建模、微分方程建模、积分建模、统计建模、概率建模、层次分析等多种方式的教学。

2.2对于数学建模方法采取分阶段的教学方式

数学建模方法的教学需要分阶段进行展开，遵循由简单到复杂，由容易到困难的阶梯状教学模式。其中，由容易到复杂可分为初级建模、典型建模与综合建模三个部分。初级建模是指数量关系比较明显，比较容易展开，运用基本的数学方法和知识就可以解决，求解简单明确，可以不用过多整理分析；典型建模是指所要探究的现实问题涉及面比较广，文字说明解释比较多，用容易的数学式子较难表述出来，需要经过判断分析，做出恰当的假设。去掉一些本质之外的因素，量与量的关系较容易发现，所求结果并不是十分精确，需要进一步的简单评价和分析说明；综合建模是指主要来源于生产生活的中的实际问题。都是没有经过转化和抽象的原始问题。问题的背景信息不明确，一般情况只有问题的基本要求和情境，在求解过程中除了数学知识，还要用到一定的在数学领域之外的知识。切入问题困难，量与量的关系也较难发现。需要花费较多的精力去收集整理和分析判断所用的信息和数据［3］。

2.3加强数学建模方法的多元化表征

对数学建模方法的教学需要从多角度多元化的表征，运用数学建模，可以用多种途径来解决现实问题，同一数学建模以不同的方式在不同的情境中可以多次出现，对于同一种数学建模方法要以不同的方式多角度多方面的分析，从而使其中隐含的关键要素不断的呈现出来，有助于学生掌握并运用到其他新的情境中去，提高对数学建模以及现实问题的灵活掌握。数学建模方法采用单一的视角和现实问题，会使学生容易错失对于数学建模的其他重要方面理解，并会导致学生在现实问题中不能够灵活多样的运用，因此在具体的教学中，注意展示数学家建模的方法间的多维关联，加强数学建模的方法的多元表征，实施对数学建模方法的多维分析［4］。

2.4将数学建模方法与现实问题联系交叉

数学建模方法的提出就是为了解决现实问题，因此在数学建模的教学中需要同具体的现实情境联系交叉。抽象的数学建模方法在现实问题的应用中存在着很多的变量，这就要求在教学中，注意覆盖多种现实问题，在丰富的现实问题中，向学生讲授数学建模方法的多个方面。由于不同问题所蕴含的情境也不相同，采用相同的数学建模方法的不同现实问题，能够反映出数学建模的方法的不同其他方面与特性，反之，对一种数学建模方法需要采用多角度的拟定问题情境，充分的展示出其数学建模方法的多样情境支持。

3　数学建模教学的教学方法的具体案例

3.1案例介绍

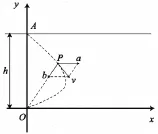
有一只鸭子想要游到河流对岸的某个位置O，若是这只鸭子的方向始终朝着河流对岸的O，求这只鸭子的游动曲线。

3.2模型假设和建立

首先假设河流两岸为平行直线，河流宽度为H；鸭子游水的速度为b，水流速度为a，两者均为常数；将鸭子出发点的位置设为A；鸭子的游动方向自始至终指向O［5］。

取O点为坐标原点，河流的顺水方向定位X轴，河流对岸则是Y轴指向。若是能求出p（x，y）关于时间t的表达式。具体如下图所示：

3.3模型计算求解

例如取a=1，b=2，h=10，t∆=0.3，则结果如下表所示：

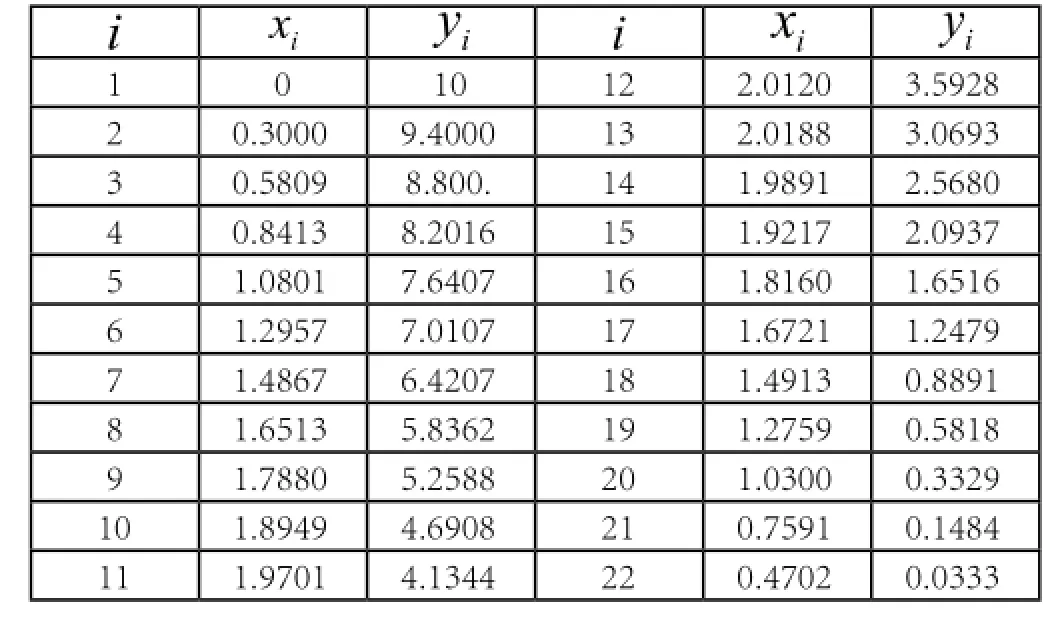
1　0　10　12　2.0120　3.5928 2　0.3000　9.4000　13　2.0188　3.0693 3　0.5809　8.800.　14　1.9891　2.5680 4　0.8413　8.2016　15　1.9217　2.0937 5　1.0801　7.6407　16　1.8160　1.6516 6　1.2957　7.0107　17　1.6721　1.2479 7　1.4867　6.4207　18　1.4913　0.8891 8　1.6513　5.8362　19　1.2759　0.5818 9　1.7880　5.2588　20　1.0300　0.3329 10　1.8949　4.6908　21　0.7591　0.1484 11　1.9701　4.1344　22　0.4702　0.0333

4　结语

综上所述，如今的大学教学中，对于数学建模的应用十分普遍，因为数学建模具有形象直观的功能，所以在数学建模讲述的案例比较容易被大家所理解，因而，数学建模得到了大学老师的重视和青睐。然而，数学建模的教学方法在实际的应用中，因为假设错误或者语言漏洞，给数学建模教学带来了严重的阻碍。基于此，为了促进数学建模的发展，必须对数据建模的教学方法存在的问题，进行妥善处理，才能进一步推动大学数学教学的进步。

［1］蒲俊，张朝伦，李顺初，等.探索数学建模教学改革提高大学生综合素质［J］.中国大学教学，2011，（12）:24-25，70.

［2］王诗云，单锋，刘勇进，等.大学生数学建模的发展历程［J］.林区教学，2012，（7）:100-102.

［3］宋云燕，朱文新.浅析大学数学教学中数学建模思想的融入［J］.教育与职业，2015，（10）:76-77.

［4］陈绍刚，黄廷祝，黄家琳，等.大学数学教学过程中数学建模意识与方法的培养［J］.中国大学教学，2010，（12）:44-46.

［5］侯晓帆，王以宁.行动学习法在教学中的应用——以数学建模实验教学为例［J］.中国电化教育，2011，（4）:105-108.

O242.1

A

1003-5168（2015）11-279-02