一种模拟岩体裂纹扩展的三角单元网格开裂技术

常 鑫，程远方，夏强平，韩修廷

（1.中国石油大学石油工程学院，山东青岛266580；2.清华大学航空航天与工程力学系，北京100084）

一种模拟岩体裂纹扩展的三角单元网格开裂技术

常 鑫1，程远方1，夏强平2，韩修廷1

（1.中国石油大学石油工程学院，山东青岛266580；2.清华大学航空航天与工程力学系，北京100084）

基于三角网格的几何特征，提出一种利用有限元方法模拟岩体裂纹扩展的三角单元网格开裂技术。该方法选取三角网格进行单元离散，采用远场围线积分计算裂尖应力强度因子，由最大周向应力准则确定裂纹扩展方向，最后通过开裂单元的网格分裂或节点移动，实现裂纹扩展的数值模拟。以有限宽中心裂纹板、曲线翼型裂纹扩展和含孔洞多裂隙岩体的裂纹扩展为例进行模拟验证。结果表明：在该方法中，裂纹可以直接劈开一个单元，或沿单元边界扩展，因此裂纹能够不受初始网格的限制沿任意路径扩展；与现有的网格重构算法相比，该方法只须对裂尖局部单元进行网格开裂或节点移动，更加简便、高效，该方法还具有较好的适用性，能够准确模拟拉伸、压剪等复杂应力状态下的裂纹萌生和扩展。

有限元法；三角网格开裂；裂纹扩展；数值模拟

岩体既非完全的连续体，也非完全的离散体，而是富含节理、裂隙等软弱结构面的地质缺陷体，极易发生脆性断裂。大量的岩土工程实践表明，岩体的失稳破坏与其内部节理、裂隙的扩展和贯通密切相关［1-8］。岩体裂纹扩展的实质是连续面到非连续面的转换，如何实现对不连续面的准确刻画是问题的关键。传统有限元方法（FEM）［9-12］模拟裂纹扩展时通常需要在裂尖构建奇异单元，且随着裂纹扩展不断地进行网格重构，该方法实现困难且低效。边界元法（BEM）［13-14］虽然避免了网格重新划分的问题，但严重依赖于问题的基本解，对于非线性、非均质等问题其优势大大降低。针对以上不足，研究者提出扩展有限元方法（XFEM）［15-17］，该方法在模拟裂纹扩展时无需重新划分网格，而是在原有网格方案基础上采用特殊的插值技术处理裂纹问题，虽然较传统FEM有了较大改进，但在处理复杂裂纹扩展时富集函数通常难以确定，且引入了附加自由度，计算量较大。笔者从三角单元几何特征出发，提出一种模拟岩体裂纹扩展的三角单元网格开裂技术，该技术只对裂尖局部单元进行网格调整，不涉及不连续位移场的处理问题，也无须引入额外自由度，并将数值模拟结果与试验结果进行对比，验证三角单元网格开裂方法的有效性。

1　基本原理

网格开裂技术的基本流程可以概括为：选取三角形非结构化网格进行单元离散；采用远场围线积分获取裂尖应力强度因子并确定裂纹扩展方向；通过开裂单元的网格分裂或节点移动，实现裂纹扩展的数值模拟。

1.1裂隙岩体的虚功方程

考虑裂隙岩体Ω，线弹性小变形，其应力和位移边界分别为Γσ和Γu，裂纹体Ω内含多条裂纹Γcr，如图1所示。

图1　裂隙岩体受力示意图Fig.1 Stress diagram of rock mass with cracks

根据虚位移原理，平衡方程的等效积分形式为

分布积分后可得如下弱形式

采用最小二乘有限元法求应力，定义泛函：

式中，σ0（u）为由变形算得的应力；σ为待求的应力。由变分原理知δF（σ）=0，可得

1.2应力强度因子计算及断裂准则确定

目前，求解复杂几何形状和复杂载荷下的混合型应力强度因子主要有权函数法、虚拟裂纹扩展法、边界配置法和J积分法等［18］，但上述方法一般对裂尖网格质量要求较高。本文中采用基于Betti功能互等定理的远场围线积分法计算裂尖应力强度因子，该方法只需要知道远离裂尖处某一积分路径上的应力解与位移解，便可计算出裂尖应力强度因子，计算结果不受裂纹几何形状的影响，而且在远场积分，裂纹尖端不需要采用特殊类型的单元，用较粗的有限元网格也可获得足够的精度。围线积分的基本原理如下。

不计体力时，均匀各向同性弹性体的Betti功能互等定理为

式中，Γ为弹性体内某闭合曲线；ui和ti为某一平衡状态下边界Γ上的位移和作用力；^ui和^ti为另一辅助平衡状态下围线Γ上的位移和作用力。

对于含裂纹体，积分围线示意图如图2所示。

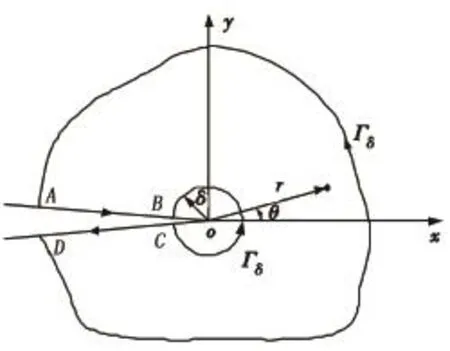
图2　积分围线示意图Fig.2 Principle diagram of contour integral

取闭合曲线Γ=Γδ′+AB+（-Γδ）+CD作为围线Γ。当裂纹面为自由面时，Betti功能互等定理等价于如下形式：

若围线Γδ取半径为δ的圆的边界，则令

式中，G为剪切模量；k=（3-ν）/（1+ν）（平面应力）或k=3-4ν，ν为材料的泊松比。

由于Γδ′为远场绕裂端的围线，ui和ti取有限元数值解，^ui和^ti分别取辅助位移场（^u^v）与辅助应力场（^σx^σy^τxy），在图2所示的局部坐标系下的表达式为

采用复化Simpson计算远场围线积分，其解为

将式（7）和式（9）代入式（6）可得

式中，KⅠ和KⅡ为应力强度因子。

比较CⅠ和CⅡ前面的系数即可得混合型裂纹的应力强度因子。

根据最大周向应力准则，裂纹开裂方向角θC为

当最大周向应力大于等于临界值时，裂纹继续扩展，此时有

1.3三角网格开裂算法

网格开裂算法遵循两大基本原则：首先，保证新旧网格之间具有较高的相容性；其次，保证对初始网格较低的依赖性。该算法主要包含破裂单元确定及单元分裂两大模块。

（1）确定破坏单元。根据最大周向应力准则计算单元破坏方向，通过矢量叉乘运算，搜索破裂方向通过单元，将该单元记为破裂单元。

（2）分裂破坏单元。沿着破裂方向与破裂单元对边交点连线将破裂单元进行单元剖分，如图3所示。

图3　三角网格开裂技术原理示意图Fig.3 Principle diagram of triangular mesh split method

详细的计算流程如下：

（1）通过远场围线积分，计算裂尖应力强度因子KⅠ、KⅡ以及裂纹开裂方向角θC，根据复合裂纹断裂准则确定开裂点。

（2）搜索包含开裂点的所有单元及单元信息。

（3）记录开裂点周围的边界信息（裂纹）即上游开裂点信息。

（4）通过裂纹开裂方向矢量与NECP中三角形单元以开裂点为起点的两条边的方向矢量做矢量叉乘运算确定开裂单元。

（5）增加与开裂点重合的节点，并求取开裂方向与开裂单元对边的交点。

（6）沿裂纹开裂方向，虚拟劈开单元，依据Delaunay准则判断网格的畸变性。

（7）若存在畸变网格，调整网格将网格棱边移至裂纹开裂方向，如图4所示。假设开裂方向为，棱边为，则将B点坐标替换为E点的值，同时将和作为裂纹边界，其中A′为第（5）步中新增节点。

（8）若不存在畸变网格，则沿开裂方向将开裂单元分裂为两个网格，增加节点E（图4），将和记为裂纹边界，同时将临开裂单元ΔBCD，在E点分裂为两个网格。

图4　网格优化Fig.4 Mesh optimization

（9）最后修正单元节点编号，顺时针侧单元用节点A表示，逆时针侧单元用节点A′表示，同时为新单元映射初始信息。

（10）重复（1）～（9），进行下一开裂点网格开裂操作。

网格调整方案如图5所示。

图5　裂纹扩展过程中的网格调整方案Fig.5 Grid adjustment programs of crack propagation process

2　裂纹扩展模拟

2.1有限宽中心裂纹板

对于特殊的含裂纹构件，已有学者求得了闭合形式解（以公式、曲线或图表的形式表示），并汇编成应力强度因子手册。以有限宽中心裂纹板为例对本程序断裂参数的计算精度进行验证。考虑如图6所示的有限宽中心裂纹板，板的半高H、半宽w和厚度B分别为200、100和1.0 mm，中心裂纹总长2a为40 mm。在板的远处承受均匀的拉应力σ=30 MPa。假设板各向同性、均匀、线弹性，弹性模量E= 200 GMPa，泊松比ν=0.3。应力强度［19］表达式为

其中F为有限宽度修正系数，典型的计算公式有以下3种。

Isida公式的近似：

修正的Koiter公式：

修正的Feddersen公式：

考虑模型对称性，取1/2模型进行分析，如图7所示。采用非结构化三角形网格进行单元离散（共11893个节点和23240个单元）。

图6　有限宽中心裂纹板Fig.6 Cracked plate of finite width center

图7　网格划分方案（1/2模型）Fig.7 Program of grid generation（1/2 model）

图8　裂纹体变形（×200倍）及裂尖前缘方向的应力云图Fig.8 Crack deformation（×200）and crack tip σystress nephogram

表1　无量纲化的应力强度因子Table 1 Dimensionless stress intensity factor

2.2压剪状态下曲线翼型裂纹扩展特性模拟

翼型裂纹的起裂、扩展及其失稳特性一直是研究脆性裂隙岩体渐近失稳破坏机制的基础，国内外众多学者对压剪状态下的翼型裂纹扩展进行了试验研究。为了验证本文中方法的准确性，将数值模拟结果与杨庆等［1］的试验结果进行对比。试验采用熟石膏作为试件材料，其弹性模量E=0.682 GPa，泊松比ν=0.32，抗拉强度为0.384 MPa，断裂韧度KIC=0.032 MPa·m1/2。试件外形尺寸为250 mm× 180 mm×20 mm，如图9所示。

图9　裂纹板几何模型Fig.9 Geometric model of cracked plate

在试件中预埋薄金属片，金属片的宽度为0.2 mm，当石膏凝结后拔出金属片，形成含预制裂纹试件，裂纹厚度为0.2 mm，裂纹的深度为20 mm。模拟不同裂纹角条件下裂纹的扩展路径，基本参数见表2。

表2　试样编号及裂纹特征Table 2 Sample number and crack characteristics

数值模型尺寸与试样尺寸相同，边界采用滑动边界，利用非结构化三角形网格进行单元离散。数值模拟开始后，计算当前载荷作用下的裂纹尖端应力强度因子KⅠ和KⅡ，并进行裂纹扩展判断，若满足式（13），则对裂纹尖端相应单元进行剖分，整个数值计算过程通过Mesh_operate.for程序自动实现。图10为试样I-2计算40步后的网格拓扑结构。图10中紫色曲线为裂纹扩展路径，与原始网格结构相比仅裂纹扩展路径附近单元发生了网格剖分，新生成的网格依然保持较高的网格质量。以试样I-2为例给出了翼型裂纹扩展的有限元实体模型，如图11所示。

图10　网格开裂后新裂纹拓扑结构（I-2）Fig.10 New crack topology structure after grid cracking（I-2）

图12为不同初始裂纹角条件下翼型裂纹形状及扩展角，给出了翼型裂纹扩展路径及扩展方向随裂纹扩展长度的变化关系。由图12可以看出：在翼型裂纹扩展中存在一条过初始裂纹中点平行于最大主应力方向的直线，随着裂纹长度增加，翼型裂纹不断逼近这条直线；同时发现在裂纹扩展初期，裂纹扩展方向变化较大，随着裂纹长度增加，裂纹扩展方向逐渐逼近90°。

图11　压剪作用下翼型裂纹扩展有限元模拟结果（I-2）Fig.11 Crack extension finite element simulation results under compression-shear action（I-2）

图12　不同初始裂纹角条件下翼型裂纹形状和扩展角Fig.12 Crack path and propagation angle under different initial crack angles

2.3含孔洞多裂纹岩体开裂过程模拟

岩石材料具有明显的非均质性，内部含有多种尺度、多种形状的孔洞、裂隙以及结构面，在工程计算领域对含孔洞多裂纹岩体开裂过程的模拟一直是一个难点问题。已有的研究大都集中在单一孔洞模型，对含孔洞多裂纹岩体的开裂过程和孔洞的存在对裂纹扩展路径的影响研究较少［20］，以双孔洞裂隙岩体为例对上述问题进行数值模拟，着重分析孔洞对裂纹扩展路径的影响，以证明网格开裂算法在模拟多裂纹扩展方面的适用性。模型结构如图13所示。

模型尺寸为D×L（127 mm×127 mm），厚度忽略不计，模型简化为平面应力问题。圆孔洞的半径为2 mm，初始裂纹长度a=2.54 mm，倾角θ=45°。其中：弹性模量E=0.689 GPa，泊松比ν=0.3，受双向拉伸载荷作用。仍然利用非结构化三角形网格进行单元离散，图14给出了计算30步后的右侧孔洞附近的网格拓扑结构，图14中紫色曲线为裂纹扩展路径，其中内侧裂纹（I-1、I-2号裂纹）在孔壁附近明显沿曲线路径扩展。

图13　含孔洞多裂纹体几何模型Fig.13 Geometric model of multiple cracks body with holes

图15为裂纹扩展过程中的第一主应力云图。从图15（a）可以看出，当内侧裂纹相遇后在孔洞内侧产生显著的应力集中，裂纹扩展发生明显偏折，呈现出“相互吸引”的特征，随着裂纹进一步扩展，内侧应力集中区域逐渐消失，相反外侧裂纹尖端处应力集中明显，如图15（b）所示。内侧裂纹同时受孔洞和原始裂隙的双重影响，扩展路径迂回曲折，而外侧裂纹呈现出近乎直线的扩展形态。图16为本文数值模拟结果与Moes等［21］的研究成果的对比，可以看出两者具有极高的吻合度。

图14　网格开裂后新网格拓扑结构Fig.14 New mesh topology structure after grid cracking

图15　裂纹扩展过程第一主应力云图（×2）Fig.15 The first principal stress nephogram during crack propagation process（×2）

图16　含孔洞多裂纹岩体裂纹扩展路径Fig.16 Crack propagation path of rock mass with holes

3　结 论

（1）采用三角单元网格开裂技术模拟裂纹扩展时，裂纹可以直接劈开一个单元或沿单元边界扩展，因此裂纹能够不受初始网格的限制沿任意路径扩展；与现有的网格重构算法相比，该方法只须对裂尖局部单元进行网格开裂或节点移动，更加简便、高效。

（2）三角单元网格开裂技术不仅具有较高的断裂参数计算精度，而且可以准确地模拟拉伸、压剪等复杂应力状态下的裂纹萌生和扩展，将为岩体基本力学性质以及岩体工程方法的基础研究提供有力支撑。

［1］杨庆，李强，赵维，等.翼型裂纹扩展特性的试验和数值分析［J］.水利学报，2009，40（8）：934-940. YANG Qing，LI Qiang，ZHAO Wei，et al.Experiment study and numerical simulation on propagation characteristrics of wing type cracks under compression［J］.Journal of Hgdraulic Engineering，2009，40（8）：934-940.

［2］陈卫忠，李术才，朱维申，等.岩石裂纹扩展的实验与数值分析研究［J］.岩石力学与工程学报，2003，22（1）：18-23. CHEN Weizhong，LI Shucai，ZHU Weishen，et al.Experimental and numerical research on crack propagation in rock under compression［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（1）：18-23.

［3］周火明，杨宇，张宜虎，等.多裂纹岩石单轴压缩渐进破坏过程精细测试［J］.岩石力学与工程学报，2010，29（3）：465-470. ZHOU Huoming，YANG Yu，ZHANG Yihu，et al.Fine test on progressive fracturing process of multi-crack rock samples under uniaxial compression［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（3）：465-470.

［4］李世愚，和泰名，尹祥础，等.岩石断裂力学导论［M］.合肥：中国科学技术大学出版社，2010：1-10.

［5］郑哲敏.连续介质力学与断裂［J］.力学进展，1982，12（2）：133-140. ZHENG Zhemin.Continuum mechanics and fracture［J］. Advances in Mechanics，1982，12（2）：133-140.

［6］唐春安，黄明利，张国民，等.岩石介质中多裂纹扩展相互作用及其贯通机制的数值模拟［J］.地震，2001，21（2）：53-58. TANG Chun'an，HUANG Mingli，ZHANG Guomin，et al.Numerical simulation on propagation interaction and coalescence of multi-cracks in rocks［J］.Earthquake，2001，21（2）：53-58.

［7］李强，张力霆，齐清兰，等.压缩载荷下闭合裂纹的曲线分支裂纹模型研究［J］.工程力学，2013，30（4）：294-300. LI Qiang，ZHANG Liting，QI Qinglan，et al.Study of the curve branch crack model for the closed flaw under compressive loading［J］.Engineering Mechanics，2013，30（4）：294-300.

［8］陈勉.页岩气储层水力裂缝转向扩展机制［J］.中国石油大学学报：自然科学版，2013，37（5）：88-94. CHEN Mian.Re-orientation and propagation of hydraulic fractures in shale gas reservoir［J］.Journal of China University of Petroleum（Edition of Natural Science），2013，37（5）：88-94.

［9］杨庆生，杨卫.断裂过程的有限元模拟［J］.计算力学学报，1997，14（4）：33-38. YANG Qingsheng，YANG Wei.Finite element simulation of fracture process［J］.Chinese Journal of Computational Mechanics，1997，14（4）：33-38.

［10］孙翔，刘传奇，薛世峰.有限元与离散元混合法在裂纹扩展中的应用［J］.中国石油大学学报：自然科学版，2013，37（3）：126-130，136. SUN Xiang，LIU Chuanqi，XUE Shifeng.Application of combined finite-discrete element method for crack propagation［J］.Journal of China University of Petroleum（E-dition of Natural Science），2013，37（3）：126-130，136.

［11］BELYTSCHKO T，BLACK T.Elastic crack growth in finite element with minimal remeshing［J］.International Journal for Numerical Method in Engineering，1999，45：601-620.

［12］DAVID A，MARCELO E，MARIA C R.Automatic LEFM crack propagation method based on local lepp-delaunay mesh refinement［J］.Advances in Engineering Software，2010，41：111-119.

［13］雷钧，黄祎丰，杨庆生.裂纹动态扩展的边界元模拟［J］.北京工业大学学报，2013，39（6）：806-810. LEI Jun，HUANG Weifeng，YANG Qingsheng.Dynamic crack propagation by boundary element method［J］. Journal of Beijing University of Technology，2013，39（6）：806-810.

［14］秦飞，岑章志，杜庆华.多裂纹扩展分析的边界元方法［J］.固体力学学报，2002，23（4）：431-438. QIN Fei，CEN Zhangzhi，DU Qinghua.Boundary element analysis of cracked bodies［J］.Acta Mechanica Solida Sinica，2002，23（4）：431-438.

［15］郭历伦，陈忠富，罗景润，等.扩展有限元方法及应用综述［J］.力学季刊，2011，32（4）：612-615. GUO Lilun，CHEN Zhongfu，LUO Jingrun，et al.A review of the extended finite element method and its applications［J］.Chinese Quarterly of Mechanics，2011，32（4）：612-615.

［16］方修君，金峰，王进廷.基于扩展有限元法的粘聚裂纹模型［J］.清华大学学报：自然科版，2007，47（3）：344-347. FANG Xiujun，JIN Feng，WANG Jinting.Cohesive crack model based on extended finite element method［J］.J Tsing Univ（Sci&Tech），2007，47（3）：344-347.

［17］刘剑，刘晓波，冯发强.基于扩展有限元法对含孔洞平板多裂纹扩展模拟研究［J］.失效分析与预防，2013，8（6）：326-330. LIU Jian，LIU Xiaobo，FENG Faqiang.Simulation study of multiple crack extension of holey plate based on extended finite element method［J］.Failure Analysis and Prevention，2013，8（6）：326-330.

［18］杨晓翔，范家齐，匡震邦.求解混合型裂纹应力强度因子的围线积分法［J］.计算结构力学及其应用，1996，13（1）：84-89. YANG Xiaoxiang，FAN Jiaqi，KUANG Zhenbang.A contour integral method for stress intensity factors of mixed-mode crack［J］.Computational Structural Mechanics and Applications，1996，13（1）：84-89.

［19］中国航空研究院.应力强度因子手册［M］.北京：科学出版社，1993：128-129.

［20］杨圣奇，吕朝辉，渠涛.含单个孔洞大理岩裂纹扩展细观试验和模拟［J］.中国矿业大学学报，2009，38（6）：774-781. YANG Shengqi，LÜ Chaohui，QU Tao.Investigations of crack expansion in marble having a single pre-existing hole：experiment and simulations［J］.Journal of China University of Mining&Technology，2009，38（6）：774-781.

［21］NICOLAS M，JOHN D，TED B.A finite element method for crack growth without remeshing［J］.International Journal for Numerical Methods in Engineering，1999，46：131-150.

（编辑 李志芬）

A triangular mesh split method for simulating crack propagation in rock matrix

CHANG Xin1，CHENG Yuanfang1，XIA Qiangping2，HAN Xiuting1
（1.School of Petroleum Engineering in China University of Petroleum，Qingdao 266580，China；2.Department of Engineering Mechanics in Tsinghua University，Beijing 100084，China）

Based on the geometrical characteristics of triangular meshes，a triangular mesh split method was proposed to simulate the propagation of cracks in rock matrix.Firstly，the rock matrix with primary cracks was divided by triangular elements. Then the stress intensity factors were calculated using a far-field contour integral，and the orientation of the crack propagation can be determined via the maximum circumferential stress criterion.Finally，the numerical simulation of crack propagation was realized by the mesh splitting or node movement.The applicability of the triangular mesh split algorithm was verified in case studies，including the crack propagation in a centrally cracked panel with a finite width，along curved wings and in a multi-fractured rock matrix with holes.The results show that the crack can split a unit element or can be extended along the mesh boundary，therefore the crack can be extended along arbitrary path without the limitation of the original mesh.Compared with the existing mesh reconstruction algorithm，this method is more convenient and efficient for use，and it can be also used effectively to simulate the initiation and propagation of cracks under complex stresses including tension，compression and shearing.

finite element method；triangular mesh split；crack propagation；numerical simulation

TU 457

A

1673-5005（2015）03-0105-08

10.3969/j.issn.1673-5005.2015.03.014

2014-07-26

“十二五”国家科技重大专项（2011ZX05037-004）；教育部长江学者和创新团队发展计划（IRT1086）

常鑫（1987-），男，博士研究生，主要从事非常规储层水力压裂裂纹扩展形态研究。E-mail：changxin7521@163.com。

引用格式：常鑫，程远方，夏强平，等.一种模拟岩体裂纹扩展的三角单元网格开裂技术［J］.中国石油大学学报：自然科学版，2015，39（3）：105-112.

CHANG Xin，CHENG Yuanfang，XIA Qiangping，et al.A triangular mesh split method for simulating crack propagation in rock matrix［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（3）：105-112.