基于Cryosat-2数据的南海2′×2′重力异常计算与分析

万剑华，李家军，刘善伟，杨俊钢

（1.中国石油大学地球科学与技术学院，山东青岛266580；2.国家海洋局第一海洋研究所，山东青岛266061）

基于Cryosat-2数据的南海2′×2′重力异常计算与分析

万剑华1，李家军1，刘善伟1，杨俊钢2

（1.中国石油大学地球科学与技术学院，山东青岛266580；2.国家海洋局第一海洋研究所，山东青岛266061）

利用Cryosat-2数据计算南海高空间分辨率高精度重力异常，对Cryosat-2 level 2 SIR_GDR-2A数据进行轨迹分析和交叉点分析。基于测高数据集（第1～4周期），借助加权最小范数最小二乘解计算网格剩余垂线偏差分量，然后计算中国南海海域（4°～24°，105°～120°）2′×2′重力异常。结果表明，Cryosat-2数据轨迹密度高且分布均匀规则，交叉点不符值均方根值为15.9cm，略高于同步时间段的Jason-2 GDR数据。与船测重力相比，中国南海海域（4°～24°，105°～120°）2′×2′重力异常误差为4.5×10-5m·s-2。

卫星测高；Cryosat-2；逆Vening-Meinesz公式；重力异常

海洋重力场对海洋油气勘探、军事国防具有重要意义，卫星测高技术是目前大面积、快速获取海洋重力场的最有效手段。众多学者联合多颗卫星测高数据开展了中国南海海域重力场的计算工作［1-6］，空间分辨率达到2′×2′，与船测重力相比，精度为（9～11）×10-5m·s-2，但这些传统卫星测高数据空间分辨率低，测高精度不同（T/P：6cm，Geosat：10～20cm，ERS-1/2：10cm），且多颗卫星测高数据之间也存在一定系统性偏差，影响重力异常计算精度，而Cryosat-2卫星的数据轨道密集，测高精度1～3cm［7-8］，笔者基于Cryosat-2测高数据计算中国南海海域2′×2′高精度重力异常。

1　Cryosat-2数据分析

Cryosat-2卫星于2010年4月8日发射成功，重复周期为369 d，子周期30 d，每周期有5344圈轨迹，在赤道上的轨道间距为7 km。其主要载荷是合成孔径/干涉高度计（SIRAL），采用延迟多普勒雷达高度计（DDA）技术。与传统的雷达高度计相比，DDA测高精度约为传统高度计的2倍，在海面平静时测高精度约为0.5cm，在海浪高度达4 m时测高精度仍能优于1.0cm。SIRAL有3种测量模式：低分辨率测量模式（LRM），对海面和平坦的冰盖内部进行测量，沿轨分辨率为5～7 km；合成孔径雷达（SAR）模式，对部分近岸海域和海冰进行测量，沿轨分辨率为250 m；合成孔径雷达干涉测量（SARIn）模式，对冰盖边缘和高山冰川进行测量，沿轨分辨率为250 m。SIRAL载荷在沿轨方向采用20 Hz测量，提高了数据分辨率和精度。

Cryosat-2 level 2 SIR_GDR_2A测高数据（1～4周期，2010.7～2013.11）研究区域内地面轨迹如图1所示，共有升轨迹255条，降轨迹234条，红色框内数据为SAR模式数据，其他为LRM模式数据（测量模式掩膜版本为3.3）。

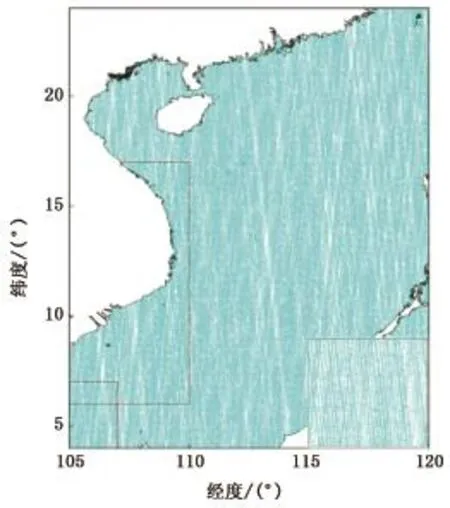
图1　Cryosat-2地面轨迹分布Fig.1 Cryosat-2 satellite altimeter data ground track distribution

1.1轨迹密度分析

Geosat/ERM、T/P、ERS-1/2、Jason-1、Jason-2和Envisat卫星重复轨道任务阶段赤道上的轨道间距分别约为164、316、80、316、316和80 km。其中T/P和Jason-1卫星经历过变轨，轨道处于原来轨道的中间，使其地面轨迹覆盖率增加1倍。多星重复轨道数据轨迹如图2所示，其构成的轨迹网格间距从几千米到一百多千米不等，数据分布比较散乱；将图1和图2对比可以看出，相对于多星重复轨道联合数据，Cryosat-2数据轨道间距小，数据密度高，且分布更加均匀规则。

图2　多星数据地面轨迹Fig.2 Multi-satellite altimeter data ground track distribution

1.2交叉点分析

交叉点不符值主要是由径向轨道误差引起，反映了卫星测高的精度。与Cryosat-2同步时间段的Jason-2 GDR数据交叉点不符值均方根（RMS）为15.1cm，Cryosat-2自交叉点不符值RMS为15.9cm，空间分布如图3所示，交叉点不符值分布均匀，没有明显的模式差异，LRM模式交叉点不符值RMS为15.4cm，与Jason-2交叉点不符值RMS相当；SAR模式交叉点不符值RMS为18.2cm，略高于Jason-2交叉点不符值RMS值。时标偏差是导致Cryosat-2交叉点不符值偏高的主要原因［9-10］，可通过时标偏差修正和交叉点平差以降低交叉点不符值［10-12］，本文中选择验后条件平差法［12］减小交叉点不符值，平差后交叉点不符值RMS值降至8.6cm。

将Cryosat-2数据与同步时间段的Jason-2数据进行互交叉点比较，验证测高数据的一致性，互交叉点不符值空间分布如图4所示，Cryosat-2 LRM模式数据交叉点不符值均值为-1.32 m，RMS为27.1cm；SAR模式数据交叉点不符值均值为-2.07 m，RMS为39.8cm。由此可知，Cryosat-2海面测高值与Jason-2测高值存在负的系统性偏差，主要原因是Cryosat-2 level 2 GDR数据没有进行海况偏差改正和内部延迟改正。本文中利用沿轨测高数据一次差分信息，借助移去-恢复技术计算重力异常，由于沿轨相邻两测高点海况偏差改正和内部延迟改正接近，故Cryosat-2测高数据的系统性偏差并不影响重力异常计算。

图3　Cryosat-2自交叉点不符值Fig.3 Crossover difference of Cryosat-2 satellite altimeter data itself

图4　Cryosat-2与Jason-2互交叉点不符值Fig.4 Crossover difference between Cryosat-2 and Jason-2

2　垂线偏差计算方法

垂线偏差法是当前利用卫星测高技术计算海洋重力场的最优方法［13］，由沿轨垂线偏差ε计算网格点垂线偏差的观测方程［14］为

式中，n为观测点的数目；υi、αi和εi分别为第i个观测点的残差、方位角和沿迹垂线偏差。

其矩阵形式为

由于系数矩阵A的元素扰动，采用间接偏差方法计算会发生矩阵秩亏，导致方程解不唯一。借助加权最小范数最小二乘解可解决矩阵秩亏问题［15］。假设矩阵A为m×n阶矩阵，对矩阵A进行奇异值分解

式中，矩阵U和V分别为m阶和n阶酉矩阵；Σ为对角矩阵。矩阵A的M-P广义逆A+为

参数X的解为

式中，P为与距离有关的权阵。

3　重力异常计算

由于垂线偏差含有丰富的重力场高频成分以及EGM2008重力场模型在长波分量上的优势，实验中采用移去-恢复方法［5］，利用沿轨迹一次差分信息，以计算网格点为中心，选取4′×4′窗口内的测高观测点，应用公式（1）～（5）计算2′×2′网格剩余垂线偏差分量，共得到251040个点。

采用逆Vening-Meinesz公式反演海洋重力异常时，剩余垂线偏差的范围会影响重力异常计算的精度。文献［4］中选取不同范围的剩余垂线偏差分量计算海洋重力场，结果表明选取5″内剩余垂线偏差分量计算的海洋重力场能够有效利用数据和保证海洋重力场的精度。据此，选取剩余垂线偏差分量绝对值小于5″的点，选择后得到232 948个点，数据剔除率为7.2%。

积分半径同样影响重力异常精度，积分半径太小，则区域内可用于计算的测高点太少，甚至没有；积分半径太大，虽然用于计算的测高点增多，但引入的海面地形影响变大，导致产生更大误差［16］。经试验比较，本文中选择积分半径为30′。由逆Vening-Meinesz公式得到中国南海海域（4°～24°，105°～120°）2′×2′重力异常，结果如图5所示。

图5　重力异常计算结果Fig.5 Gravity anomalies

4　结果分析

本文中采用船测重力数据检验重力异常计算结果的精度，经过精度控制和网格化处理，精度为（1～3）×10-5m·s-2，数据范围如图6所示，红色点代表船测重力异常点，相邻数据点距离为30′。

图6　船测重力数据点Fig.6 Shipboard gravity data points

以卫星测高数据计算的2′×2′重力异常网格数据为基础数据，内插出船测数据点重力异常，与船测数据作差比较，结果见图7。从图7中可看出，由卫星测高数据计算的重力异常与船测重力异常值非常接近，但并不完全相等。将本文重力异常结果与船测重力作差比较，差值最大值为18.9×10-5m·s-2，最小值为-11.8×10-5m·s-2，RMS为4.5×10-5m· s-2，考虑到船测重力精度，由卫星测高数据计算的重力异常精度可能会更高，且两者之间存在正的系统偏差，偏差值为1.4×10-5m·s-2。

图7　重力异常比较散点图Fig.7 Diagram of gravity anomaly comparison

（1）与文献［2-4］结果相比，重力异常空间分辨率相当，与船测数据差值绝对值的最大值明显减小，减小了约20×10-5m·s-2，RMS由（9～11）×10-5m· s-2降低到4.5×10-5m·s-2，精度明显提高，与文献［6］结果相比，RMS减小1.2×10-5m·s-2，但空间分辨率由2.5′×2.5′提高到2′×2′。相较于多星数据联合计算海洋重力异常，Cryosat-2测高数据轨道密集，精度高，并避免了多颗卫星数据之间参考椭球和参考框架不统一的问题，这是本实验取得高精度结果的主要原因。

（2）为研究卫星测高重力与船测重力差值的分布特点，本文中对差值数据进行统计分析，统计直方图如图8所示，分级统计结果如表1所示。由图8和表1可知，差值主要集中在（7～8）×10-5m·s-2，占全部测点数的90.5%，小于-7×10-5m·s-2或大于8×10-5m·s-2的点数只有21个点。本文结果与国内外同行结果相比，差值绝对值明显减小，减小了约20×10-5m·s-2。

图8　重力异常比较差值分布直方图Fig.8 Histogram of gravity anomaly difference

本文中仅用了4个周期的测高数据，随着Cryo-sat-2卫星测高数据的积累和数据质量的改善及卫星测高数据处理技术的进步，可进一步提高重力异常计算的精度。另外，在Cryosat-2测高数据基础上，联合其他测高精度较高的卫星测高数据，有望进一步提高海洋重力异常的空间分辨率和精度。

表1　测高重力异常与船测数据差值分级统计Table 1 Comparison between altimeter-derived and shipboard gravity anomalies with different ranges

5　结 论

（1）在网格剩余垂线偏差分量计算中，利用加权最小范数最小二乘解的奇异值分解方法求解方程，能有效解决因系数矩阵秩亏导致的方程解不唯一问题。

（2）Cryosat-2测高数据空间分辨率和测高精度高于传统卫星测高数据，基于该测高数据的南海海域2′×2′重力异常计算精度为4.5×10-5m·s-2，较国内外同行提高（4～6）×10-5m·s-2。

致谢 感谢欧空局（ESA）提供Cryosat-2卫星数据。

［1］HWANG C.Inverse vening meinesz formula and deflection-geoid formula：applications to the predictions of gravity and geoid over the South China Sea［J］.Journal of Geodesy，1998，72：304-312.

［2］王海瑛，王广运.卫星测高数据的沿轨迹重力异常反演法及其应用［J］.测绘学报，2001，30（1）：21-26. WANG Haiying，WANG Guangyun.Inversion of gravity anomalies from along-track vertical deflections with satellite altimeter data and its applications［J］.Acta Geodaetica et Cartographica Sinica，2001，30（1）：21-26.

［3］李建成，宁津生，陈俊勇，等.联合TOPEX/Poseidon，ERS2和Geosat卫星测高资料确定中国近海重力异常［J］.测绘学报，2001，30（3）：197-202. LI Jiancheng，NING Jinsheng，CHEN Junyong，et al. Determination of gravity anomalies over the South China Sea by combination of topex/poseidon，ERS2 and Geosat altimeter data［J］.Acta Geodaetica et Cartographica Sinica，2001，30（3）：197-202.

［4］胡淑梅，文汉江，李洪超，等.利用多种测高数据反演中国南海海域重力异常［J］.大地测量与地球动力学，2011，31（4）：56-59. HU Shumei，WEN Hanjiang，LI Hongchao，et al.Inversion of gravity anomalies over South China Sea by use of combination of multi-satellite altimeter data［J］.Journal of Geodesy and Geodynamics，2011，31（4）：56-59.

［5］王虎彪.用卫星测高和船测重力资料联合反演海洋重力场［D］.武汉：中国科学院测量与地球物理研究所，2005. WANG Hubiao.Inversion of marine gravity anomalies by combinating multi-altimeter data and shipborne gravimetric data［D］.Wuhan：Institute of Geodesy and Geophysics，Chinese Acaderny of Sciences，2005.

［6］DADZIE I，LI J，CHU Y.Prediction of gravity anomalies over the South China and Philippine seas from multi-satellite altimeter sea surface heights［J］.Geo-Spatial Information Science，2008，11（3）：174-179.

［7］SANDWELL D，GARCIA E，SOOFI K，et al.Toward 1-mgal accuracy in global marine gravity from Cryosat-2，envisat，and Jason-1［J］.The Leading Edge，2013，32（8）：892-899.

［8］STENSENG L，ANDERSEN O B.Preliminary gravity recovery from Cryosat-2 data in the Baffin Bay［J］.Advances in Space Research，2012，50（8）：1158-1163.

［9］GOMMENGINGER C，MARTIN-PUIG C，DINARDO S，et al.Improved altimetric performance of Cryosat-2 sar mode over the open ocean and the coastal zone［C］.Vienna：European Geosiciences Union，c2012.

［10］汪栋，范陈清，贾永君，等.HY-2卫星雷达高度计时标偏差估算［J］.海洋学报，2013，35（5）：87-94. WANG Dong，FAN Chenqing，JIA Yongjun，et al.The time tag bias estimation of hy-2 satellite radar altimeter［J］.Acta Oceanologica Sinica，2013，35（5）：87-94.

［11］翟国君，黄谟涛，谢锡君，等.卫星测高数据处理的理论与方法［M］.北京：测绘出版社，2000：119-123.

［12］刘传勇，暴景阳，黄谟涛，等.验后平差方法在Geosat/ERM卫星测高数据处理中的应用［J］.海洋测绘，2008，28（1）：5-8. LIU Chuanyong，BAO Jingyang，HUANG Motao，et al. The application of posteriori compensation theory of error in altimeter data set from geosat/erm crossover adjustment［J］.Hydrographic Surveying and Charting，2008，28（1）：5-8.

［13］彭富清，夏哲仁.卫星测高中的垂线偏差法［J］.海洋测绘，2004，24（2）：5-9. PENG Fuqing，XIA Zheren.Vertical deflection theoremof satellite altimetry［J］.Hydrographic Surveying and Charting，2004，24（2）：5-9.

［14］HWANG C，Eu-CHI K，BARRY P.Global derivation of marine gravity anomalies from seasat，geosat，ers-1 and topex/poseidon altimeter data［J］.Geophys J Int，1998（134）：449-459.

［15］鲁铁定，陶本藻，周世健.矩阵的SVD分解性质及其在秩亏网平差中的应用［J］.大地测量与地球动力学，2007，27（5）：63-67. LU Tieding，TAO Benzao，ZHOU Shijian.Characteristics of matrix SVD and its applications to rank deficiency free network adjustment［J］.Journal of Geodesy and Geodynamics，2007，27（5）：63-67.

［16］李娜，章传银.用逆Vening-Meinesz公式反演海洋重力场时积分半径的选择［J］.大地测量与地球动力学，2009，29（6）：126-129. LI Na，ZHANG Chuanyin.Option of integral radius in inversion of sea gravity with inverse vening-meinesz formula［J］.Journal of Geodesy and Geodynamics，2009，29（6）：126-129.

（编辑 修荣荣）

Calculation and analysis of 2′×2′gravity anomalies over the South China Sea based on Cryosat-2 satellite altimeter data

WAN Jianhua1，LI Jiajun1，LIU Shanwei1，YANG Jungang2
（1.School of Geosciences in China University of Petroleum，Qingdao 266580，China；2.First Institute of Oceanography，State Oceanic Administration，Qingdao 266061，China）

The gravity anomaly of the South China Sea was calculated with high spatial resolution and precision using the Cryosat-2 data.The tracks and crossover points of the Cryosat-2 satellite altimetry level 2 SIR_GDR_2A data were analyzed.The component of grid residual vertical deflection was calculated with the weighted minimum least squares solution method using the cycle1-cycle4 data，then the gravity anomalies in 2′×2′grid over the South China Sea between 4°-24°latitude and 105° -120°longitude were determined.The results show that the Cryosat-2 data have a high track density，and are distributed regularly and uniformly with a 15.9cm RMS value of crossover point differences，which is slightly higher than the synchronous Jason-2 GDR data.Compared with the post-processed shipboard gravimetry，the root mean square value of the gravity anomaly in 2′×2′grid over the South China Sea is 4.5×10-5m·s-2.

satellite altimetry；Cryosat-2；inverse Vening-Meinesz formula；gravity anomaly

P 228.3

A

1673-5005（2015）03-0070-06

10.3969/j.issn.1673-5005.2015.03.009

2014-06-30

海洋公益性行业科研专项（201305032）；中欧龙计划合作项目（ID.10466）

万剑华（1966-），男，教授，博士，研究方向为“3S”在海洋领域中的应用和数字海洋关键技术。E-mail：wjh66310@163.com。

刘善伟（1982-），男，讲师，博士，研究方向为海洋遥感。E-mail：shanweiliu@163.com。

引用格式：万剑华，李家军，刘善伟，等.基于Cryosat-2数据的南海2′×2′重力异常计算与分析［J］.中国石油大学学报：自然科学版，2015，39（3）：70-75.

WAN Jianhua，LI Jiajun，LIU Shanwei，et al.Calculation and analysis of 2′×2′gravity anomalies over the South China Sea based on Cryosat-2 satellite altimeter data［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（3）：70-75.