材料科学基础课程晶体结构概念上现存误区的探讨
毛卫民
北京科技大学 北京 100083
晶体结构是材料科学基础课程重要而基础性的知识。[1]在当前的教学实践中尚存在一定的概念误区,值得探讨和改进。通常采用14种布拉菲点阵描述实际晶体可能存在的各种平移对称性,且用不同点阵的单胞常数表达不同的平移对称规律。[2]另一方面,根据晶体的主要点对称特征又可以把晶体归结成7种不同的晶系。[2]如果不注意区分晶体这两类对称性的差异,就会造成用描述晶体平移对称性的单胞常数特征区分晶体所属晶系的不当阐述,而晶体所属晶系本来只能根据其点对称特征区分。在现有教科书中代表性的非严谨表达为:“根据晶胞的6个参数可以把14种空间点阵归纳为七大晶系”。相应习题为“已知某一晶体单胞的常数为a=b=c且α=β=γ=90°,试判断该晶体所属的晶系”时,典型的非严谨答案为:该晶体一定属于“立方晶系”。这种误区在本科教学阶段往往并不会直接造成即刻而显著的不良后果。但当学生进入深层次的学习和研究时,尤其在许多新材料及其相关结构的分析研究时常常会造成明显的困扰。
1 晶体平移对称性的确认
多数材料均具备一定的晶体结构。晶体被定义为结构基元三维长程有序排列的固体物质,因此平移对称性是晶体的核心特征。图1左侧显示了由A,B,C三种原子所构成晶体的一个晶胞,用a,b,c和α,β,γ表示该晶胞的3个棱边长及棱边之间的夹角,用实线、矢量线、虚线等表示原子间不同的键合方向和性质。将这个晶胞在三维空间根据a,b,c和α,β,γ等晶胞参数作周期性平移就可以构造出整个晶体结构。可以看出,平移时晶胞中A,B,C原子及原子间不同的结合键都会以a,b,c和α,β,γ等晶胞参数为单位作周期性平移。通常用点阵表达晶胞内所有组成部分的这种相同的平移规律,可简略地用点阵单胞表示;相应的单胞常数也是a,b,c和α,β,γ,如图1右侧所示,可见其中表示平移的几何点并不是各向同性的。人们熟知,现存大量晶体的平移对称性各有差异,但总体只可能有14种不同性质的平移规律,可用十四种布拉菲点阵来表示(见表1)。
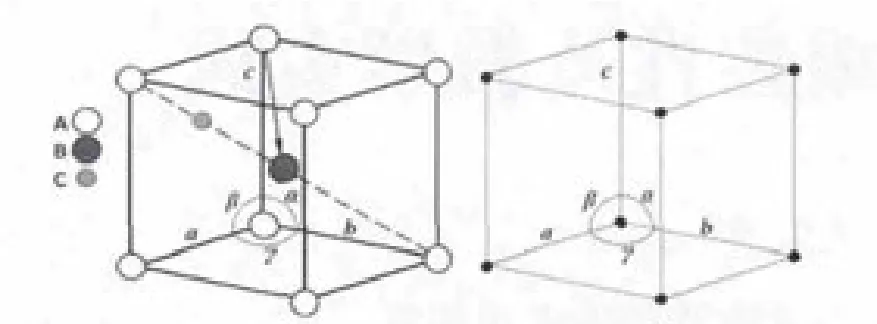
图1 由A,B,C三种原子所构成晶体的晶胞(左)及表达其平移对称性的点阵单胞(右)

表1 表达晶体平移对称性的14种布拉菲点阵
不论晶胞的a,b,c是否相等,α,β,γ是否为90º或其他特征角度,在描述晶体平移对称性时并未能直接说明晶体是否具备任何旋转对称性,或称点对称性。可见晶胞的边角关系并不必然说明晶体所具备的点对称性及所属的晶系。
2 晶体的点对称性
晶体所具备的旋转、反演、平面反映、旋转反演等非平移对称性统称为点对称性。从点对称性的角度出发,根据晶体所具备最高的点对称性或主要的点对称性特征可以把晶体划分成七大类,称为7种晶系(见表2)。根据各晶系的点对称性特征可以从理论上推导出[2]其晶胞的边、角之间有一些特定的关系或规律(见表2),如对立方晶系必有a=b=c且α=β=γ=90°。因此,是晶体的点对称性特征决定了其单胞、即其平移对称行为必须遵守的规则。
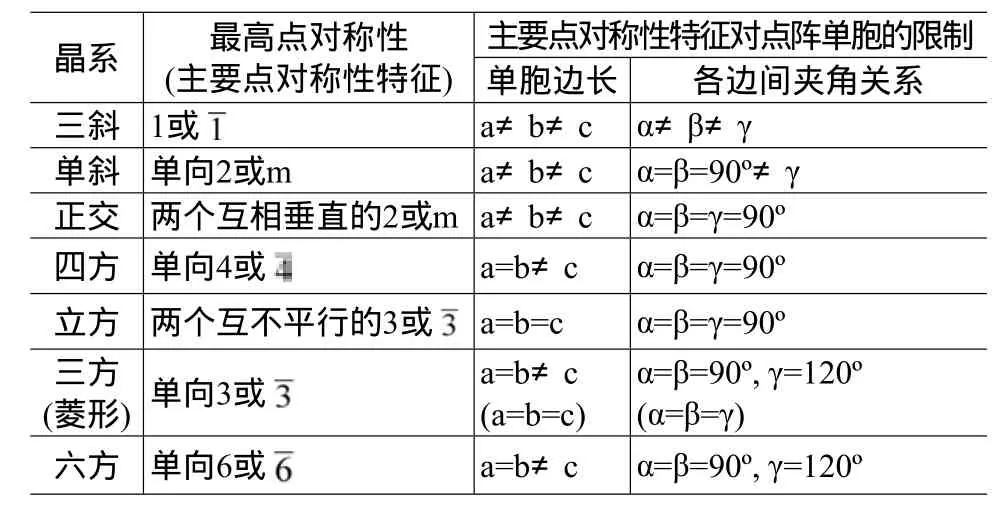
表2 7种晶系的主要点对称特征及其晶胞的边角关系
3 晶体结构的对称性与晶胞常数
如图1所示的晶体结构,即使在a=b=c且α=β=γ=90°的情况下也不可能属于立方晶体,因为该晶胞不存在立方晶体所要求的2个互不平行的3次对称轴。换句话说,已知晶体的主要点对称特征可以判定出其晶胞常数之间的特定关系;而仅知道晶胞常数存在特定关系并不能准确判断晶体所属的晶系。因此可见,表1和表2中晶胞或单胞边角关系的“≠”号是不要求相等,不是不允许相等。
当前新材料研究中经常需要分析新结构或新相及其特性。许多学生在测得其点阵常数后就急于判定其所属晶系,并对后续研究工作造成困扰。例如,FeS2晶体可以具备三斜、正交、立方等多种不同的晶体结构。检测发现[3],其晶胞常数为a=b=c=0.541 7 nm,且有α=β=γ=90º;分析其晶胞结构发现各原子在晶胞内的占位情况(见表3)使其无法具备立方结构,因此只能属于三斜晶系。此时若草率地认为其具备立方结构就会给后续研究造成误导。
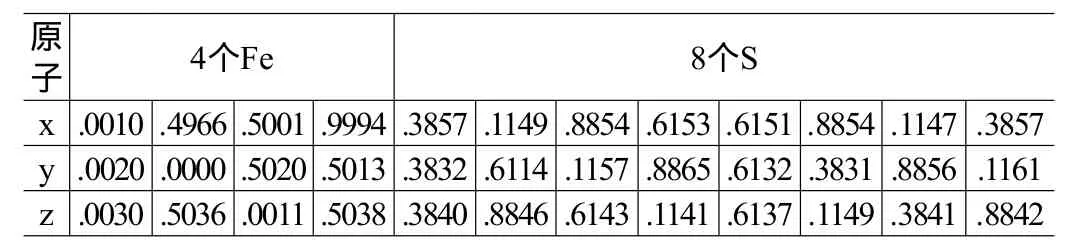
表3 三斜晶系FeS2晶胞内各原子的位置[3](x,y,z取值0~1,分别表示晶胞常数a,b,c的分数)
4 问题与总结
现有材料科学基础课程教材或课件对晶体结构的描述中常见到:“根据晶胞的六个参数可以把14种空间点阵归纳为七大晶系” “通常是根据六个点阵参数的相互关系,考虑晶胞棱边是否相等以及是否是直角,可以把空间点阵分为七种类型,称为七大晶系”“根据6个点阵参数间的相互关系,可将全部空间点阵归属于7种类型,即7个晶系”“晶系与布拉菲点阵:按棱长a,b,c和夹角α,β,γ分为七大晶系”“按晶胞外形即棱边长度之间的关系和晶轴夹角情况归类,每一个类别即一个晶系,晶系只有7种”“在晶体学中,根据棱边长度a,b,c是否相等、晶轴间夹角α,β,γ分是否相等、是否为直角等因素,又可以把这14钟空间点阵归纳为七大晶系”等描述。如上分析可知这类根据晶体平移规律来确定晶系的描述并不很严谨,也容易导致学生的误解。
在讲解晶胞常数时应注意:晶胞边角关系仅说明晶体的平移对称特征,晶胞任何特殊边角关系都不可直接用于判别晶系。是晶体的点对称性决定了其晶胞必备的特定边角关系,晶胞边角关系中的≠为不要求相等,非不允许相等。
[1]余永宁.材料科学基础[M].第二版.北京:高等教育出版社,2012.
[2]毛卫民.材料的晶体结构原理[M].北京:冶金工业出版社,2007.
[3]Bayliss P. Crystal structure refinement of a weakly anisotropic pyrite[J]. American Mineralogist, December, 1977(62): 1168-1172.

