一种新的低频超宽带干涉合成孔径雷达绝对相位估计方法
许军毅 安道祥 黄晓涛 王广学
一种新的低频超宽带干涉合成孔径雷达绝对相位估计方法
许军毅①安道祥*①黄晓涛①王广学②
①(国防科学技术大学电子科学与工程学院 长沙 410073)②(空军预警学院信息对抗系 武汉 430019)
该文针对低频超宽带(UWB)干涉合成孔径雷达(InSAR),提出一种新的干涉相位绝对值估计方法。该方法首先对干涉图像进行非参数模型的精配准,并利用配准偏移量生成配准相位。然后将配准相位从干涉相位中去除,得到失配相位。最后估计失配相位的绝对相位,进而得到绝对干涉相位的值。该方法利用失配相位具有无相位缠绕或只在相干性较差区域存在相位缠绕的特性估计其绝对相位,相比传统的绝对干涉相位估计方法具有更小的运算复杂度。P波段UWB InSAR实测数据处理结果验证了该方法的有效性。
干涉合成孔径雷达;超宽带;绝对相位
1 引言
交轨干涉合成孔径雷达(InSAR)能够利用雷达回波的相位信息获取地面高度,被广泛应用于地形测绘中。InSAR处理流程可以分为绝对相位值估计与高程反演两部分[1]。前者是为了获取代表波程差的干涉相位真实值,后者将该相位转换为地面高度信息。其中获取高精度的干涉相位是高程反演的关键,也是InSAR研究的重点。
频域的方法实际上是通过对SAR图像的频谱进行分割实现多通道干涉[7,8]中多频干涉的目的。具有代表性的频域方法主要有两种,即谱分割算法[5](split-spectrum algorithm)与多频分析(Multi Chromatic Analysis, MCA)的算法[9,10]。这两种算法均对信号的频谱进行了分割。前者获得了两个子频段的干涉图,并将两个干涉图进行求差,再乘以一个比例系数,即可得到子频段干涉的绝对相位,再利用估计得到的绝对相位为辅助估算全频段干涉相位解缠后的残余相位模糊。而MCA则是获得两个以上的子频段,并采用线性回归的方法估算子频段的绝对干涉相位。选取估算结果中高质量的点与全频段的干涉相位解缠结果进行对比,即可估计残余相位模糊[10]。频域的方法具有运算速度快的特点,但由于需要进行频谱分割,以提取子频段,因此该类算法主要用于绝对带宽较大的情况[9]。
本文的研究针对相对带宽大于0.2的低频(载频小于1 GHz)超宽带(Ultra-WideBand, UWB) InSAR数据[11]。低频UWB InSAR系统结合了低频信号的叶簇穿透特性,以及超宽带信号的高分辨优势,主要用于丛林地区的数字地形模型(Digital Terrain Model, DTM)反演研究。由于干涉相位大小与波长成反比,因此,为了得到对高度较灵敏的干涉相位图,低频干涉需要很长的干涉基线。这使得数据的采集不得不以重航过模式(repeat-pass mode)进行。虽然如此,由于低频UWB InSAR具有很大的相对带宽,且长波信号对地表的小尺度变化不敏感,因此低频UWB InSAR数据依然能够获得较强的空间相关性,甚至在植被覆盖区域也是如此[12]。此外,由于图像分辨率接近信号波长量级,因而在一个分辨单元内,等效散射中心个数较少。相比窄带干涉,超宽带干涉受相干斑影响较小。
低频SAR系统的绝对带宽通常不大,但具有很大的相对带宽。例如瑞典的CARABAS系列低频UWB SAR系统,绝对带宽仅为70 MHz[13],但相对带宽却大于1.2。这种相对带宽大的特性为其估计绝对相位带来优势。文献[6]中曾指出,利用相对带宽较大的特性,UWB InSAR的绝对相位估计过程有可能被简化,使得无需进行相位解缠,或相位解缠复杂度变小。
无需相位解缠的情况在瑞典防务研究局(FOI)的研究人员利用CARABAS系列低频UWB SAR系统(相对带宽约为1.2)开展重轨干涉试验时得到了验证。其提出了一种新的绝对相位计算方法[13]。原理为:首先,以小于一半聚焦深度(Depth Of Focus, DOF)为间隔,将待处理图像在不同参考高度上进行重采样;然后,以相关系数作为准则,判断每个像素的最佳参考高度,并将相同最佳参考高度的区域作为一个子图像;最后,将不同子图像分别在不同参考高度上进行干涉处理。由于相对带宽大于1,因而DOF的一半小于模糊高度[13],从而获取的干涉相位是无缠绕的。这一方法避免了相位解缠。然而,当相对带宽小于1时,其子图像内相位还是会出现缠绕。一种解决办法是减小重采样参考高度的间隔,使其小于模糊高度。然而,对像素参考高度的估计能力往往是有限的,当参考高度间隔很小时,其估计精度难以满足,且运算复杂度大大增加。针对这种情况,只能采用别的方法进行绝对相位估计。
本文针对UWB InSAR信号特点,提出一种新的绝对相位估算方法。该方法根据InSAR图像配准精度与干涉相位的关系,利用非参数模型配准方法,将干涉相位真实值的估算转换为对代表配准误差的失配相位计算。理论推导表明,若配准精度足够高,失配相位无缠绕或缠绕只发生在少数低相干区域。这一特性使得绝对相位估计过程被大大简化。
本文内容安排如下:第2节描述了本文方法的理论依据;第3节阐述了本文方法的关键步骤及实现流程;第4节利用重航过P波段UWB SAR实测数据验证了本文方法的有效性;第5节总结全文。
2 理论依据
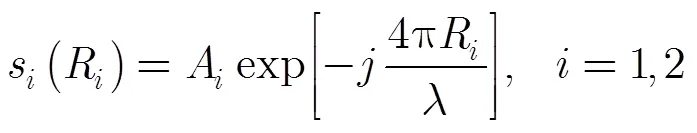
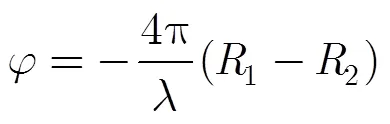

图1 干涉测量几何原理
干涉测量首先要对主图像与辅图像进行配准,使得图像中的点能一一对应,再进行共轭相乘以得到干涉相位。设经过配准在辅图像中的位置为,则有

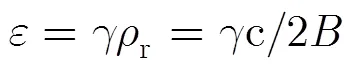
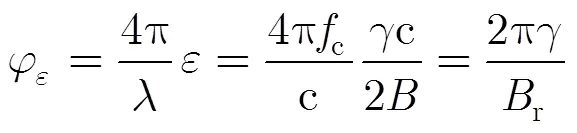
从式(5)可知,若配准误差系数满足条件:
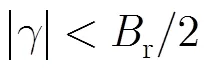
3 本文方法
基于前文的理论分析可知,高精度的配准结果能够直接确定绝对干涉相位。然而,在实际使用中,还存在多个问题需要解决。其中包括如何获取高精度的图像配准结果,以及当图像中存在配准精度不满足式(6)条件时的处理。
3.1 UWB InSAR图像配准
现有干涉配准算法通常将主、辅图像间的变换表示为参数模型[14],模型的参数借助控制点的配准偏移量进行估计。考虑低频UWB InSAR的基线通常较长,主图像与辅图像因入射角的差异,对地形的几何形变存在不可忽略的差异,因而不能采用参数模型的方法估计配准偏移量[15]。本文采用如下的非参数模型方法:
(1)基于相关法对主图像与辅图像作全局粗配准,使得图像能够初步对应起来。
(2)在主图像中等间隔布置控制点,并采用实相关函数法对控制点做局部亚像素级配准,得出所有控制点的配准偏移量。其中以控制点为中心截取的图像块大小为128像素×128像素[15]。
(3)再对图像中阴影等相关性较小区域的控制点进行校正[13]。这些区域内控制点的配准偏移量通常与周围存在明显差异,类似噪声,通过与周围控制点的偏移量进行对比即可检测出。校正时,利用周围正确的控制点偏移量,采用线性插值的方法计算该点偏移量[13]。
(4)对控制点的偏移量进行内插,得出所有位置的配准偏移量。
第(4)步中控制点内插的方法获得的实际是原配准偏移量的下采样后再上采样的结果,等同于进行了低通滤波。控制点的间隔越小,分辨能力越强,则配准误差越小。此外,考虑到对控制点配准时,截取的图像块的大小为128像素×128像素,相邻点截取的图像块之间存在很大的重复区域,因此相邻点计算得到的配准偏移量差异通常较小。为了降低运算复杂度,而又不引入过大误差,本文设置控制点的间隔为10个分辨单元(此时,相邻两个控制点截取的局部图像块重合面积超过了90%)。这种内插的方法在地形变化缓慢的地区能够取得较高的精度。而在地形变化剧烈的区域,则精度较低。总的来讲,设定控制点的间隔越大,配准误差的分布方差也越大。
在得到高精度的配准偏移量后,对辅图像进行重采样并与主图像进行共轭相乘即可得到原始干涉相位。同时,根据式(3),还可得到配准相位。将配准相位转换为复数数据取共轭与原始干涉相位的复数数据相乘,所得到的结果的相位即为失配相位。
3.2失配相位解缠
由于干涉图像中不可避免地存在一些相干性较小的区域,其配准精度可能会出现不满足式(6)的情况。此外,前文的分析均是基于获得的干涉相位绝对精确、系统参数无误差的前提。在实际测量中,由于配准误差、图像去相关以及SAR系统自身的测量误差等因素,获得的干涉相位包含大量噪声,在进行噪声抑制后,干涉相位与失配相位也会存在误差。即使配准精度达到式(6)要求,可能也会存在相位缠绕,此时相位解缠不可避免。
但需要指出的是,当配准误差过大时,失配严重将导致错误的干涉相位,无法用于测量高度。这里假设配准误差不应超出0.5个分辨单元,否则认为得到的干涉相位无意义。根据式(6)可知,相对带宽大于1的InSAR数据,失配相位应是无缠绕的,这与文献[13]方法的基本要求一致。在实际情况中,配准误差通常也远优于0.5个分辨单元,因而对于相对带宽大于1的InSAR数据,相位解缠是不必要的。
对于相对带宽处于0.2~1.0之间的数据,由于并不能完全保证失配相位的无缠绕,因此需要进行相位解缠。考虑到失配相位在高相干区域通常能够满足式(6)的条件,因而这些区域通常不存在相位缠绕。若对失配相位进行解缠,难度要比直接对干涉相位进行解缠容易。
本文引入Flynn的最小不连续算法[16,17]进行相位解缠。该算法是一种基于范数准则的全局最优化算法[17],通过最小化相位图中的不连续点个数来实现相位解缠。由于该算法实现了全局的最优化解缠,因而能够提供高质量的解缠结果。该算法通过多次迭代来减少图像中的不连续点个数,解缠过程往往耗时很大[17]。但由于算法的运算复杂度与图像中的不连续点个数相关,而失配相位图中不连续点数量很少,因而对其进行解缠时,运算复杂度相比解缠常规的干涉相位要小很多。
3.3 残余相位模糊估计
路径追踪类的相位解缠算法最终获得的相位是一个相对相位,与真实相位之间还存在的常数偏差,称之为残余相位模糊。由本文第2节分析可知,失配相位在高相干区域主要分布在区间,相位的缠绕值为0。而当存在残余相位模糊时,解缠相位对应的缠绕值变为。因而若能够分辨出相位图像中的高相干区域,则残余相位模糊可通过式(7)估算。
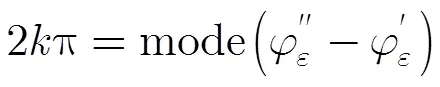
在本文中,高相干区域通过计算图像的相关系数来区分。根据文献[18]的研究可知,相关系数越大,配准精度越高。设定相关系数的阈值可确保挑选配准精度较高区域进行残余相位模糊估计。事实上,本文实验部分的结果还表明,配准误差与对应的失配相位分布类似于高斯分布。分布的均值接近0,且误差越大,出现的概率越小。因此,根据概率理论,配准误差的方差越小,样本的数量越多,式(7)中的众数运算得到的结果可信度越高。在实际应用中,为了获取较小的配准误差方差,需要设定较大的相关系数阈值,然而过大的阈值会导致样本数量过少。权衡之下,本文取相关系数的阈值为0.5。大于这一阈值的像素点通常具有较高的配准精度,且数量较多。
还应指出的是,由于系统噪声、配准误差等因素影响,原始干涉相位存在大量的噪声,从而得到的失配相位也是存在噪声的。在本文处理方法中,采用均值滤波器对失配相位中的噪声进行了抑制。滤波一方面能够降低相位解缠难度,另一方面也能减少其对残余相位模糊估计的影响。
3.4处理流程
图2为本文方法的最终处理流程。首先,采用非参数模型方法对主图像与辅图像进行亚像素级的配准。然后,利用配准结果得到干涉相位与配准相位,将配准相位从干涉相位中去除后,得到失配相位。接下来,根据相对带宽的大小选择相位解缠与残余相位模糊估计或直接得到无缠绕的失配相位。最后,将得到的失配相位与配准相位相加即为干涉相位的绝对值。
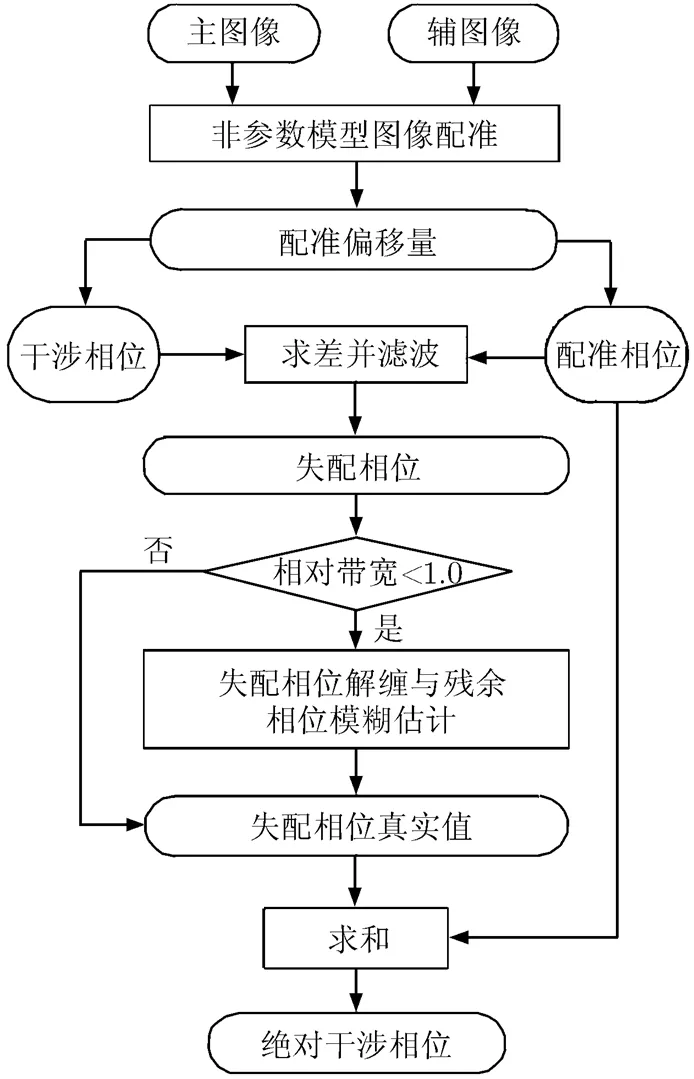
图2 本文方法处理流程
4 实测数据处理与分析
4.1 UWB SAR实测数据
为验证本文方法的有效性,本文利用某机载P波段UWB SAR系统录取的重航过实测数据,进行了重轨干涉处理。被处理数据的相对带宽约为0.25,分辨率约为1.5 m×1.5 m(距离向×方位向)。两次飞行航迹几乎平行,干涉基线长度约为100 m,与水平方向垂直,“模糊高度”为6~8 m。图3为某地区在两次航过中的成像结果。为保证相位精度,我们采用后向投影(Back-Projection, BP)算法进行成像处理。此外,飞行过程中,由于受到空中气流影响,载机飞行航迹并不是理想直线,出现了轻微的偏移。因此,成像过程中还采用了基于机载GPS录取测量数据的运动补偿。选取的主图像大小为1.1 km×1.0 km(距离向×方位向),辅图像大小为1.3 km×1.0 km(距离向×方位向)。两幅图像以相同的参考高度被重采样为地距图像,左侧为雷达近端。图3(c)中还给出了从Google Earth软件中截取的图像场景光学图像。图像中比较突出有3种地貌,即上方的A区域、中间的B区域以及下方C箭头所指公路。其中A区域为山丘地形,并覆盖有明显的植被。B区域为在山丘地形上的居民区,为人造地物。C箭头所指的公路由于表明较平,难以形成较强的雷达后向散射,因而在SAR图像中表现为很暗的亮度。图像中其他的地区地形整体变化较为缓慢,并覆盖有一定的植被。
4.2 试验结果与分析
图4给出了非参数模型方法的配准结果。图4(a)为距离向偏移量,图4(b)为方位向偏移量。图4(c)为根据配准结果计算的相关系数图。配准后对应区域在图3中用方框标出。观察图4(a)的配准结果与图3中的地形,可以看到距离向的偏移量与地形相关。这说明地形的起伏用参数模型拟合会带来很大的误差,因此必须使用非参数模型的方法进行配准。
基于图4中的配准结果,可得到图3中主图像与辅图像方框区域内的干涉相位,结果如图5(a)中所示。图5(a)中能够观察到清晰的干涉条纹,此时干涉相位中不仅包含噪声,还因为相位缠绕而呈现出条纹状。观察图4(c)中的相关系数图与图5(a)中的干涉相位图可发现,在场景中的A区域,即使存在大量植被覆盖,低频UWB InSAR也能够获得较高的相关性与较清晰的干涉条纹(雷达照射阴影区域除外)。图4(c)中同样存在多处相关系数很小的区域。较突出的是在B区域的居民区与阴影,以及C箭头所指的公路区域。对于公路与阴影区域,由于雷达回波较弱,导致图像信噪比低,因而相干性较差。而居民区则由于结构复杂,以不同角度成像时,回波特性差异较大,因而图像相关性差,难以获得较高的配准精度,从而导致较低的相关性。这些相关系数很小的区域在干涉相位图中表现为噪声相位,干涉条纹难以辨别。下面分别采用传统的方法与本文方法对获得的干涉条纹进行处理。
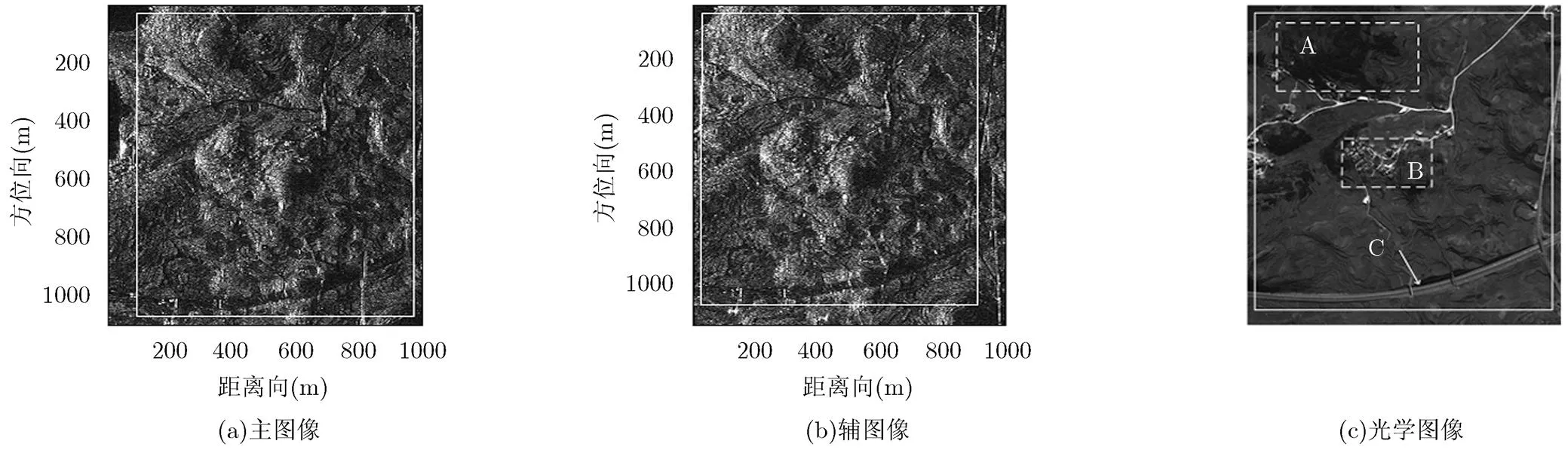
图3 P波段UWB SAR实测数据及场景光学图像

图4 图像配准结果
首先给出传统方法的处理结果。在传统的处理方法中,首先进行平地相位去除、噪声抑制等处理,结果如图5(b)所示。其中,平地相位是根据参考高度计算得出,而噪声抑制则采用了窗口大小为9像素×9像素的均值滤波。去平地相位后的干涉相位仍然存在较严重的缠绕,采用Flynn的最小不连续解缠方法进行解缠后,还需要估计残余相位模糊。本文使用残余偏移量估计的方法(具体步骤见文献[5])估计传统相位解缠结果的残余相位模糊。图5(c)为得到的绝对干涉相位结果。为方便查看,去除了其中的平地相位成分。
接下来给出本文方法的处理结果。图5(d)为利用配准结果计算得到的配准相位。将其中的平地相位成分去除,结果如图5(e)所示,相位的大小与地形相关。将配准相位从原始干涉相位中去除(即将图5(d)中相位从图5(a)中减去,采用复数共轭相乘实现)得到失配相位。同样采用窗口大小为9像素×9像素的均值滤波器进行噪声抑制后的结果如图5(f)所示。图5(f)中大量的相位缠绕被消除,仅有少数区域仍然存在缠绕。这表明所使用的配准算法不论是在山丘地形还是在平缓地形均能够达到绝对相位估计所需的配准精度。利用Flynn的方法对图5(f)进行解缠,并以相关系数图为参考,选出相位图中相关系数大于0.5的点估算残余相位模糊。最终得到失配相位的绝对相位估计结果如图5(g)所示。将失配相位与配准相位相加即可得到干涉相位的绝对值。图5(h)为本文方法估计的绝对干涉相位去除平地相位后的结果。
为证明本文方法的相位解缠结果与传统方法的一致性,用图5(h)减去图5(c),结果如图5(i)所示。计算其柱状图,结果如图6所示。从图中可以看到两者的差异集中在零相位附近,均值为0.0235 rad,方差为0.8364 rad。这证明了本文方法的绝对相位估计结果与传统方法是一致的。存在较小的相位差异主要由相位滤波引起。传统方法的滤波对象是去平地相位后的干涉相位,而本文方法滤波的对象是失配相位。此外,两种方法在低相干区域的解缠结果还存在较大的差异,这是因为低相干区域相位表现为噪声形式,存在大量的残差点,而残差点在原始干涉相位与失配相位的滤波结果中位置并不相同,从而导致最终的解缠差异。

图5 P波段实测数据处理结果
图7给出了失配相位的统计分布柱状图,这一结果也反映了配准误差的分布。从图中可以看出,其分布近似于高斯分布(分布均值为-0.4191 rad,方差为1.7758 rad),误差越大,出现的概率越小。根据统计,其中约90%的相位分布于区间。这进一步说明了式(7)中采用众数运算确定残余相位模糊的正确性。此外,还说明了本文方法对残余相位模糊的估计精度还取决于失配相位分布的方差大小。方差越小,则估计出正确结果的概率越高。而噪声等对失配相位的影响,会增加失配相位分布的方差(即使经过噪声抑制),此时需要增加样本数量来提高估计精度。
最后,表1给出了本文方法与传统方法在相位解缠与残余相位模糊估计时的耗时对比。运行程序的计算机CPU主频为3.2 GHz,内存为8 GB,程序代码在Matlab平台上运行。从表1中可以看到,传统干涉相位解缠耗时是失配相位解缠耗时的约15倍。这表明采用本文方法能够大大简化相位解缠的复杂度。此外,在残余模糊相位估计时,传统方法需要大量子图像块的配准偏移量估计运算,耗时巨大。而本文方法仅需一次众数统计运算,耗时几乎可以忽略。两者相比,本文方法在运算速度上具有很大的优势。
表1耗时对比(s)

方法相位解缠残余相位估计 传统方法55.710122.943 本文方法 3.510 0.140
5 结束语
本文针对低频UWB InSAR提出一种新的绝对相位估计方法。该方法利用了非参数模型的图像配准结果,将干涉相位估计转换为失配相位真实值估计。失配相位仅与配准精度以及信号的相对带宽相关。在高相干区域,失配相位具有无缠绕或缠绕值为的特性,因而利用这一特性能够很容易地确定解缠相位的残余相位模糊。本文方法利用了低频超宽带SAR信号的分辨率与波长相当的特性,简化了绝对相位估计的过程,特别是降低了相位解缠的复杂度。P波段UWB InSAR实测数据处理结果验证了本文方法的有效性。
此外,本文方法还需要进一步改进。一方面,需要研究更加稳定可靠的方法去判断失配相位是否需要相位解缠。另一方面,本文方法对配准精度的依赖较大,若能进一步改进配准算法的精度,则本文方法的精度与效率都会得到提高。
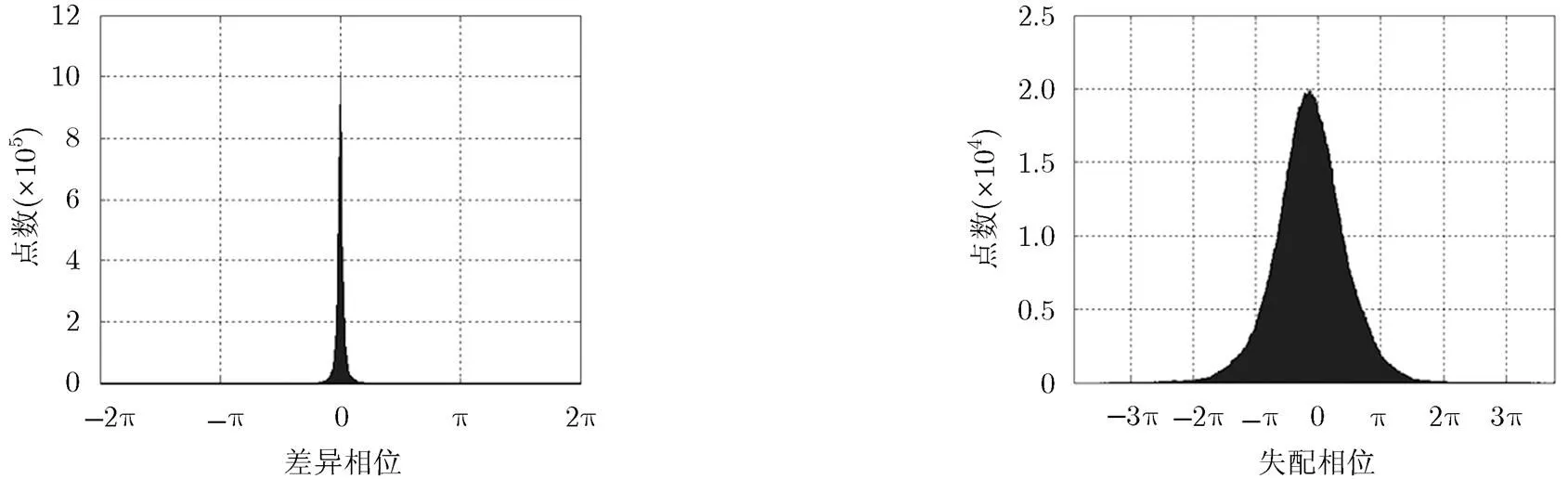
图6 本文方法与传统方法结果对比柱状图 图7 失配相位分布统计结果
[1] Rosen P A, Hensley S, Joughin I R,.. Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382.
[2] Zhong H P, Tang J S, Zhang S,.. A quality-guided and local minimum discontinuity based phase unwrapping algorithm for InSAR/InSAS interferograms[J]., 2014, 11(1): 215-219.
[3] Yu H, Xing M, and Bao Z. A fast phase unwrapping method for large-scale interferograms[J]., 2013, 51(7): 4240-4248.
[4] Liu G, Wang R, Deng Y K,.. A new quality map for 2-D phase unwrapping based on gray level co-occurrence matrix[J]., 2014, 11(2): 444-448.
[5] Madsen S N. On absolute phase determination techniques in SAR interferometry[C]. Proceedings SPIE Conference on Radar Sensor Technology, Orlando, 1995: 393-401.
[6] Bamler R and Eineder M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems[J]., 2005, 2(2): 151-155.
[7] 袁志辉, 邓云凯, 李飞, 等. 改进的基于最大似然估计的多通道InSAR高程重建方法[J]. 电子与信息学报, 2013, 35(9): 2161-2167.
Yuan Z H, Deng Y K, Li F,.. Improved multichannel InSAR height reconstruction method based on maximum likelihood estimation[J].&, 2013, 35(9): 2161-2167.
[8] Liu H, Xing M, and Bao Z. A cluster-analysis-based noise- robust phase-unwrapping algorithm for multibaseline interferograms[J]., 2015, 53(1): 494-504.
[9] Bovenga F, Giacovazzo V M, Refice A,.. Multichromatic analysis of InSAR data[J]., 2013, 51(9): 4790-4799.
[10] Bovenga F, Rana F M, Refice A,.. Multichromatic analysis of satellite wideband SAR data[J]., 2014, 11(10): 1767-1771.
[11] Federal Communications Commission (FCC). Revision of part 15 of the commission’s rules regarding ultra-wideband systems: First report and order[S]. 2002.
[12] Ulander L M H and Frolind P. Ultra-wideband SAR interferometry[J].1998, 36(5): 1540-1550.
[13] Frölind P and Ulander L M H. Digital elevation map generation using VHF-band SAR data in forested areas[J]., 2002, 40(8): 1769-1776.
[14] Sansosti E, Berardino P, Manunta M,.. Geometrical SAR image registration[J]., 2006, 44(10): 2861-2870.
[15] Fritz T, Rossi C, Yague-Martinez N,.. Interferometric processing of TanDEM-X data[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 2011: 2428-2431.
[16] 钟何平, 唐劲松, 张森. 一种基于质量引导和最小不连续合成的InSAR相位解缠算法[J]. 电子与信息学报, 2011, 33(2): 369-374.
Zhong H P, Tang J S, and Zhang S. A combined phase unwrapping algorithm based on quality-guided and minimum discontinuity for InSAR[J].&, 2011, 33(2): 369-374.
[17] Ghiglia D C and Pritt M D. Two-dimensional Phase Unwrapping: Theory, Algorithms, and Software[M]. New York: John Wiley & Sons. Inc, 1998: 151-172.
[18] De Zan F. Accuracy of incoherent speckle tracking for circular gaussian signals[J]., 2014, 11(1): 264-267.
A Novel Absolute Phase Determination Approach for Low Frequency Ultra-wideband SAR Interferometry
Xu Jun-yi①An Dao-xiang①Huang Xiao-tao①Wang Guang-xue②
①(,,410073,)②(,,430019,)
Estimation of topography for the generation of Digital Elevation Models (DEM) requires the absolute interferometric phase. However, the existing absolute phase determination methods are complicated for processing the Ultra-WideBand (UWB) Synthetic Aperture Radar Interferometry (InSAR) data. To resolve this problem, a new approach is proposed in this paper. First, to acquire the high accuracy image registration result, the registration offsets are obtained from the interpolation of the offsets of the control points. Then, based on the offsets, the interferometric phase is computed and divided into two partsthe Registration Phase (RP) and the MisRegistration Phase (MRP). The RP is derived from the registration offsets, and the MRP is dependent on the unknown misregistration. Theoretical derivations show that the MRPs are unambiguous in most high coherence areas, so MRP can be unwrapped efficiently, and its absolute phase can be obtained directly without using any auxiliary data. Finally, the absolute interferometric phase is obtained from adding the RP and the true MRP. Compared with the existing algorithms, the proposed approach has lower complexity. Experimental results on P-band UWB InSAR data prove its effectiveness.
Synthetic Aperture Radar Interferometry (InSAR); Ultra-WideBand (UWB);Absolute phase
TN957.52
A
1009-5896(2015)11-2705-08
10.11999/JEIT141334
2014-10-20;改回日期:2015-08-13;
2015-08-28
安道祥 daoxiangan@nudt.edu.cn
国家自然科学基金(61571447, 61201329)
The National Natural Science Foundation of China (61571447, 61201329)
许军毅: 男,1987 年生,博士生,研究方向为InSAR.
安道祥: 男,1982 年生,博士,讲师,从事低频超宽带SAR成像与超高分辨聚束式SAR成像技术研究.
黄晓涛: 男,1972 年生,博士生导师,教授,主要从事SAR信号处理、阵列信号处理、谱分析等信号与信息系统领域的研究工作.
王广学: 男,1981年生,博士,讲师,主要从事SAR目标检测等领域的研究工作.

