E.Ghys猜想的注记

郭亚晓，杨将

(西北大学数学学院，陕西 西安　710127)

E.Ghys猜想的注记

郭亚晓，杨将

(西北大学数学学院，陕西 西安710127)

通过类比自治动力系统中拓扑熵指数收敛的定义，给出了非自治拓扑熵指数收敛的定义及非自治Lipschitz系统中E.Ghys猜想成立的充分条件与必要条件，推广了自治动力系统中的相关结论.

非自治动力系统；拓扑熵；熵维数；Lipschitz系统.

1　引言

1965年，文献[1]定义了紧致拓扑空间上的连续自映射拓扑熵，它是一个测量系统复杂程度的不变量.1971年，文献[2]引入生成集和分离集的概念，对紧度量空间上的连续自映射定义了等价的拓扑熵，使人们对这一概念有了更直观清晰的认识.

对于有限维紧无边黎曼流形M，若f：M→M 是C1映射，Kushnirenko定理[3]给出了拓扑熵的上界

对于更一般的 Lipschitz系统，则 htop(f)≤dimEX·lnL(f)，其中 (X，d)是紧度量空间，f：X→X是Lipschitz映射，dimEX是熵维数，L(f)是映射f的Lipschitz常数.

对于给定的动力系统(X，f)，由于拓扑熵与度量无关，故

其中D是诱导相同拓扑的度量的集合，Ld(f)为相对于度量d的Lipschitz常数.

不等式(1)给出了拓扑熵、熵维数及Lipschitz常数三者的关系.之后，E.Ghys给出E.Ghys猜想，将不等式(1)变为等式

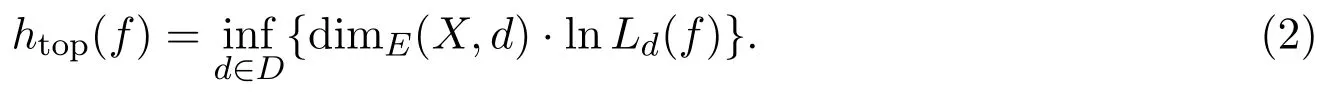
2009年，文献[4]给出了等式(2)成立的充要条件为拓扑熵指数收敛.

本文所做的工作是在文献[4]的研究基础上引入非自治拓扑熵指数收敛的概念，并且给出非自治Lipschitz系统中E.Ghys猜想成立的一个充分条件和一个必要条件.

2　预备知识

定义 2.1设(X，f1，∞)为非自治紧动力系统，若任意fi都是Lipschitz映射，则(X，f1，∞)为非自治Lipschitz动力系统.

记Sd(r)为半径为r的开球所形成X覆盖的最小基数.

定义 2.2[6]设(X，d)为紧度量空间，其熵维数定义为：

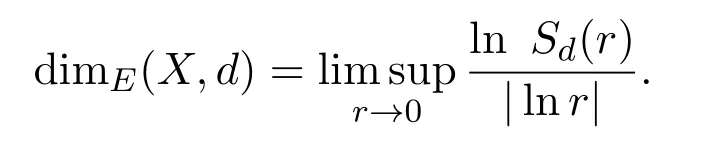
定义2.3[5]设n∈Z+，任意ε＞0，称X的一个子集F为X的相对度量d的(n，ε)生成集，如果任意x∈X，存在y∈F使得

记Md(f1，∞，n，ε，X)为相对度量d的(n，ε)生成集的最小基数.

定义 2.4[5]设(X，f1，∞)为非自治动力系统，映射f1，∞的拓扑熵定义为：

定义2.5设(X，f1，∞)为非自治动力系统，非自治拓扑熵指数收敛是指任意δ＞0，存在与原度量d等价的度量dδ和常数Cδ＞0，εδ＞0，使得对于任意0＜ε＜εδ，N＞Cδ·|lnε|，不等式

成立.

3　非自治动力系统中E.Ghys猜想成立的充分与必要条件

文献[5]给出非自治Lipschitz动力系统中拓扑熵、熵维数、Lipschitz常数三者不等关系式

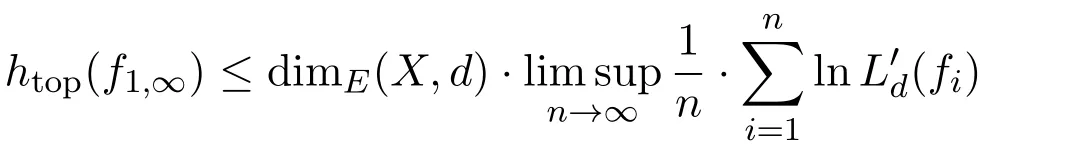
(其中L′d(fi)=max{1，Ld(fi)}，而Ld(fi)为fi相对于度量d的Lipschitz常数)的证明.为了证明的完整性，下面给出证明过程.

定理 3.1[5]设(X，f1，∞)为非自治Lipschitz动力系统，则

其中L′d(fi)=max{1，Ld(fi)}.

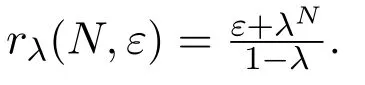
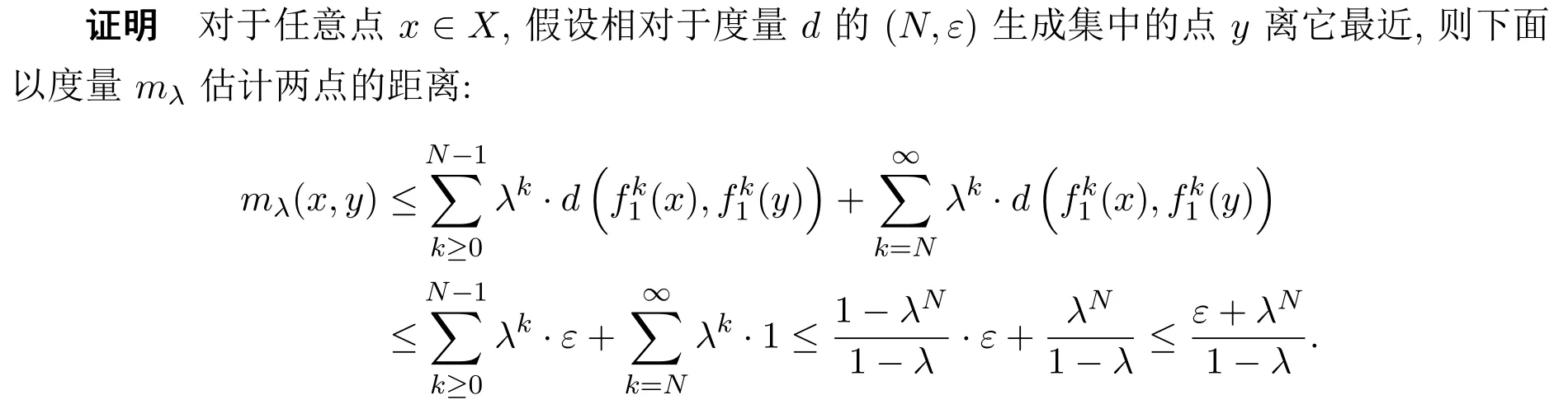
推论 3.1对于任意r＞0和λ∈(0，1)，设

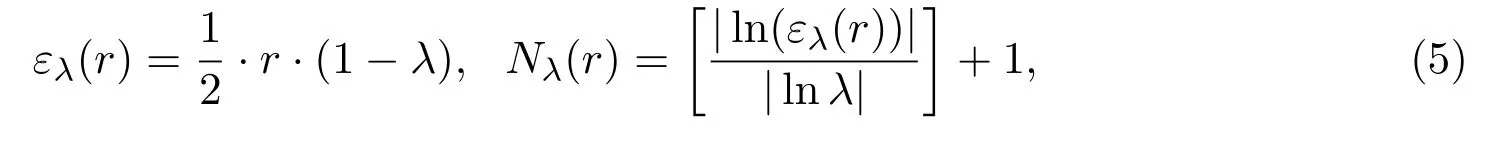
则Smλ(r)≤Md(f1，∞，Nλ(r)，ελ(r)，X).

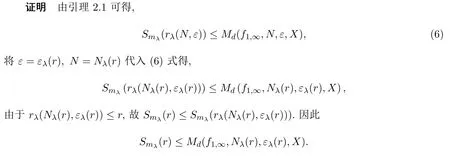
引理 3.2设 (X，f1，∞)为非自治动力系统，若非自治拓扑熵指数收敛，则存在常数λδ＞ 0，rδ＞0，对于任意0＜r＜rδ，λδ＜λ＜1，下列不等式成立

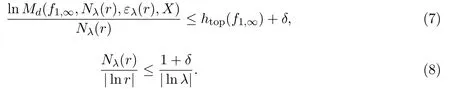
因此存在λδ＞0，rδ=min(r1，r2)＞0，对于任意0＜r＜rδ，λδ＜λ＜1时，不等式(7)(8)同时成立.

定理 3.2设(X，f1，∞)为非自治Lipschitz动力系统，若非自治拓扑熵指数收敛，且对任意λ∈(0，1)时，存在与原度量d等价的度量mλ，若对于任意i∈Z+，映射fi相对度量mλ的Lipschitz常数则等式

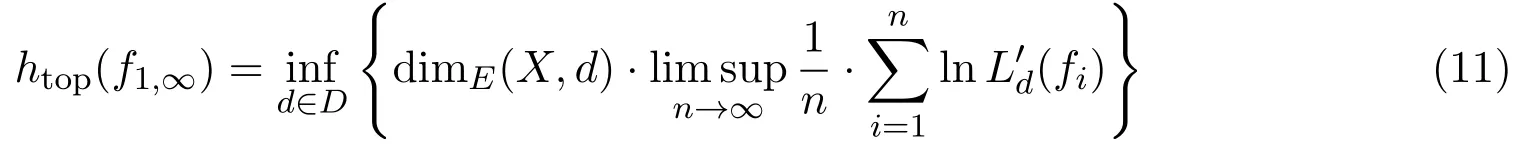
成立，其中L′d(fi)=max{1，Ld(fi)}.

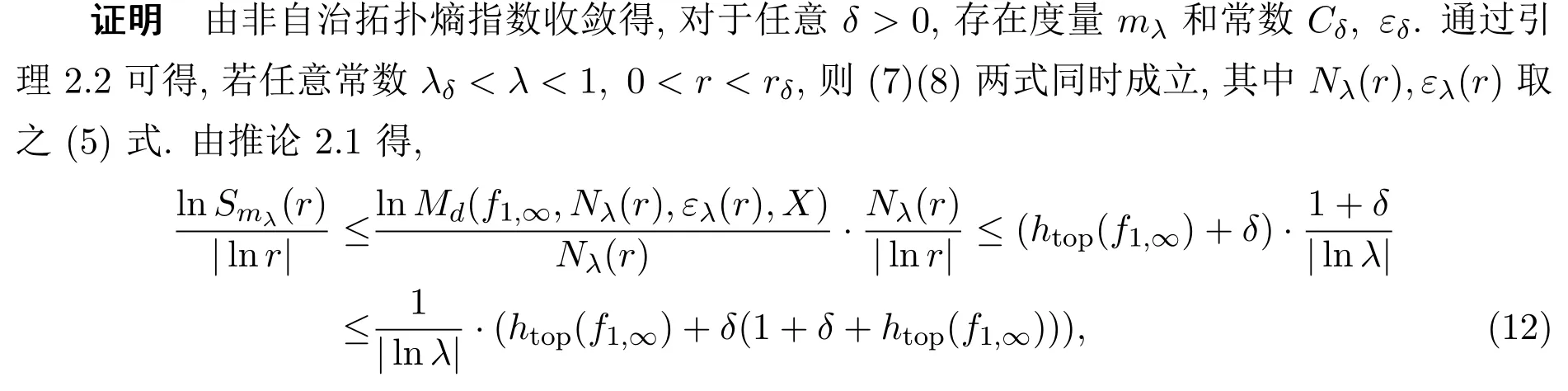
下面给出等式(11)式成立的必要条件.

定理3.3设(X，f1，∞)为非自治Lipschitz系统，等式

[1]Adler R L，Konheim A G，McAndrew M H.Topological entropy[J].Trans.Amer.Math.Soc.，1965，114：309-319.

[2]Bowen R.Topological entropy and Axiom A[J].Proc.Sympos.Pure.Math.，1971，14：23-42.

[3]Kushnirenko A G.An upper bound for the entropy of a classical system[J].Dokl.Akad.Nauk.SSSR.，1965，161：360-362.

[4]Saltykov P S.On the relation between topological entropy and entropy dimension[J].Matematicheskie Zametki，2009，86：280-289.

[5]Zhu Yujun.Entropy of nonautonomous dynamical systems[J].J.Korean Math.Soc.，2012，1：165-185.

[6]Kenneth Falconer.Fractal Geometry：Mathematical Foundations and Applications[M].America：Wiley，2013.

The remark on E.Ghys conjecture

Guo Yaxiao，Yang Jiang
(College of Mathematics，Northwest University，Xi′an710127，China)

In this paper，through analogy to the definition of topology entropy exponential convergence of the automomous dynamical system，we obtain the nation of nonautonomous topological entropy exponential convergence，and we also give the sufficient condition and the necessity condition of E.Ghys conjecture in the nonautonomous Lipschitz dynamical systems，such that we expand the related solution of application of the automomous dynamical system.

nonautonomous dynamical systems，topological entropy，entropy dimension，Lipschitz system

O189

A

1008-5513(2015)01-0065-08

10.3969/j.issn.1008-5513.2015.01.008

2014-09-15.

国家自然科学基金(11301417).

郭亚晓(1989-)，硕士生，研究方向：拓扑动力系统.

2010 MSC:37B40