具有奇性与真空粘性依赖于密度的非牛顿流局部强解的存在唯一性

张蕊，方莉

(西北大学数学学院，陕西 西安　710127)

具有奇性与真空粘性依赖于密度的非牛顿流局部强解的存在唯一性

张蕊，方莉

(西北大学数学学院，陕西 西安710127)

研究一维有界区间上粘性依赖于密度且具有奇性、初始允许真空的可压缩非牛顿流.通过正则化奇性项以及逐步迭代构造初边值问题的逼近解，对逼近解取极限得到其局部强解的存在唯一性，进一步推广了相关文献中关于非牛顿流解的存在性结果.

可压缩非牛顿流；局部强解；粘性依赖于密度

1　引言

考虑一维情形下，粘性依赖于密度的一类可压缩非牛顿流初边值问题：

初边值条件为：

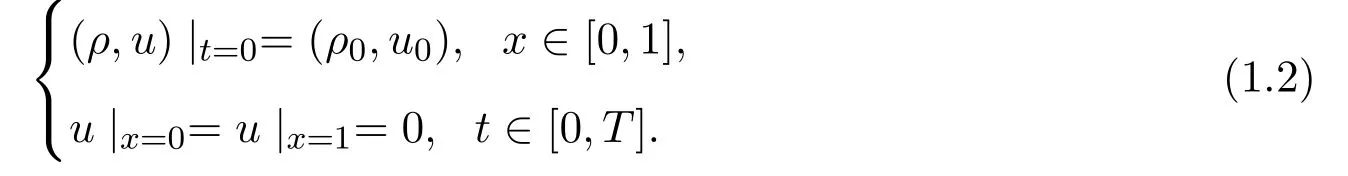
其中，ρ，u和π分别表示密度、速度和压力，ρ0≥0，1＜p＜2，α∈(0，1).由于π(ρ)中的常数A并不影响后面的分析，因此不失一般性，设A=1.为方便叙述，记I=[0，1].

对于可压缩牛顿流(p=2)，许多数学工作者已得到当初始密度具有真空时解的存在性理论并在可压Euler方程或可压Navier-Stokes方程的背景下，得到了关于初值具有紧支撑的强解的存在性结果[1-8].近年来，对于可压非牛顿流的研究也有了一些进展[9-14].

本文主要得到了初边值问题(1.1)式-(1.2)式的局部强解的存在唯一性.以下给出局部强解的定义及本文的主要结果.

定理 1.1设(ρ0，u0)满足以及相容性条件：

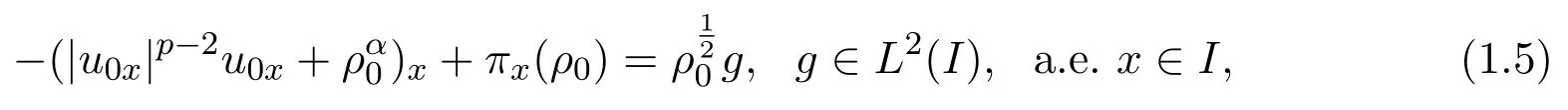
则存在T∗∈(0，T)以及初边值问题(1.1)-(1.2)的唯一强解(ρ，u)满足：

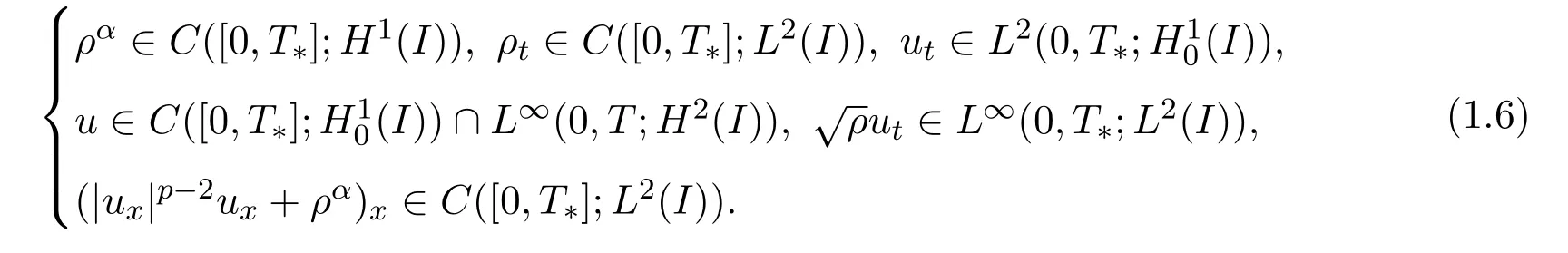
注记 1.1本文中，|·|表示Banach空间上的范数.

2　预备知识

引理 2.1[11]设Ω是R1中的有界集，1≤q≤p≤+∞.则

引理 2.2[11]设在∂Ω上f=0且则特别地，当1＜q＜+∞时，其中，Ω是R1中有界开集，d(Ω)表示Ω的长度.

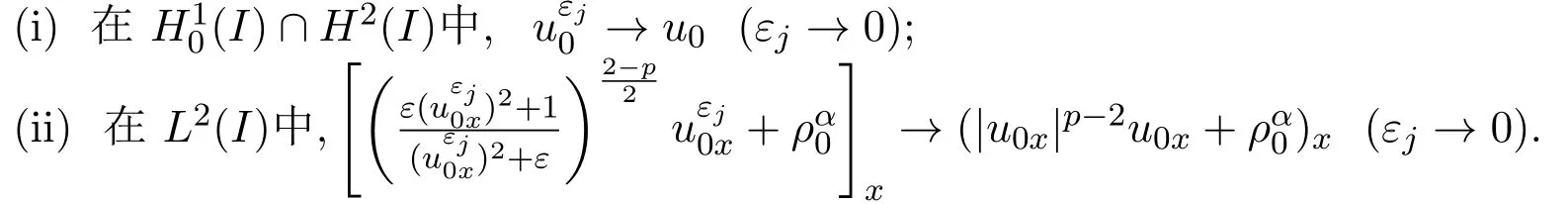
3　逼近解的构造及一致估计

4　逼近解的收敛性

5　定理 1.1的证明

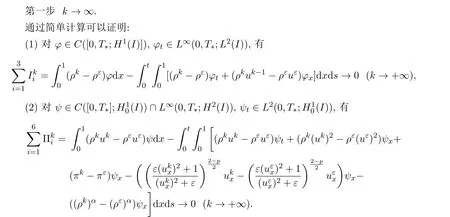
[1]Cho Y，Choe H，Kim H.Unique solvability of theinitial boundary valueproblems for compressible viscous fluids[J]，J.Math.Pures.Appl.，2004，83：243-275.

[2]Choe H，Kim H.Strong solutions of the Navier-Stokes equations for isentropic compressible fluids[J].J. Differential Equations，2003，190：504-523.

[3]Choe H，Kim Hyunseok.Global existence of the radially symmetric solutions of the Navier-Stokes equations for isentropic compressible fluids[J].Math.Methods Appl.Sci.，2005，28：1-28.

[4]Liu T，Xin Z，Yang T.Vacuum states of compressible flow[J].Discrete Contin.Dyn.Syst.，1998，4：1-32.

[5]Xin Z.Blow-up of smooth solutions to the compressible Navier-Stokes equations with compact density[J]. Comm.Pure.Appl.Math.，1998，51：229-240.

[6]Yang T，Yao Z，Zhu C.Compressible Navier-Stokes equations with density-dependent viscosity and vacuum[J].Comm.Partial Differential Equations，2001，26：965-981.

[7]Yang T，Zhu C.Compressible Navier-Stokes equations with degenerate viscosity coefficient and vacuum[J]. Comm.Math.Phys.，2002，230：329-363.

[8]Málek J，Nečas J，Rokyta M，et al.Weak and Measure-Valued Solutions to Evolutionary PDEs[M].New York：Chapman and Hall，1996.

[9]NečasováŠ，Lukáčová M.Bipolar isothermal non-Newtonian compressible fluids[J].J.Math.Anal.Appl.，1998，225：168-192.

[10]Bae H O.Existence，regularity，and decay rate of solutions of non-Newtonian flow[J].J.Math.Anal.Appl.，1999，231：467-491.

[11]Yuan H，Xu X.Existence and uniqueness of solutions for a class of non-Newtonian fluids with singularity and vaccum[J].J.Differential Equations，2008，245：2871-2916.

[12]Bognár G.Similarity solution of boundary layer flows for non-Newtonian fluids[J].Int.J.Nonlinear.Sci. a Numer.Simulat.，2009，10：1555-1566.

[13]Yuan H，Li H.Global existence and uniqueness of solution for a class of non-Newtonian Fluids[J].J.Partial Differential Equations，2012，25：13-36.

Existence of solutions for a class of non-Newtonian fluids with density-dependent viscosity，singularity and vacuum

Zhang Rui，Fang Li

(College of Mathematics，Northwest University，Xi′an7110127，China)

This paper aims to discuss existence and uniqueness of local strong solutions for a class of compressible non-Newtonian fluids with density-dependent viscosity，singularity and vacuum in one-dimensional bounded intervals.By regularizing the viscosity term with singlarity and iterating step by step，we construct the approximate solutions and prove the existence and uniqueness of the local strong solution.Furthermore，we extend the existence results in relative

for non-Newtonian fluids.

compressible non-Newtonian fluid，local strong solution，density-dependent viscosity

O175.2

A

1008-5513(2015)01-0097-014

10.3969/j.issn.1008-5513.2015.01.012

2014-05-02.

陕西省科技计划项目(2012JQ020).

张蕊(1990-)，硕士生，研究方向：偏微分方程.

2010 MSC:35A25