巧用数形结合 提高解题效率

邵燕文

摘要 数形结合是数学的基本解题方法，它包括“以形助数”和“以数解形”两个方面。在解决数学问题时，将抽象的数学语言同直观的图形相结合，实现抽象的概念与具体形象的联系和转化，使数与形的信息相互渗透，开拓了解题思路，使许多数学问题简单化。本文结合中学教材，举例说明“以形助数”和“以数解形”在解决数学问题中的一些用法。

关键词 抽象 抽象 以形助数 以数解形

中图分类号：G633.6 文献标识码：A 文章编号：1002-7661（2015）08-0070-02

“数”和“形”是组成数学的两大要素。数学家华罗庚说过：“数与形本是两依倚，焉能分作两边飞。数缺形时少直观，形少数时难入微。”教师在课堂教学过程中，要结合教材内容，根据学生实际，结合数学知识，采用教者有意、学者无心的方法，反复向学生介绍数形结合的方法。

所谓数形结合，包括两个方面的内容，其一为“从几何直观的角度，利用几何图形的性质研究数量关系，寻求代数问题的解决方法（即以形助数）；其二是利用数量关系来研究几何图形的性质，解决几何问题（即以数解形）”。它将抽象的语言和直观的图形（几何性质）结合起来，使抽象思维和形象思维结合起来，实现抽象概念与具体形象的联系和转化，实质就是“将较难问题转化为较易问题，将未知问题转化为已知问题，将复杂问题转化为简单问题”。

一、“以形助数”

每个学生在日常生活中都具有一定的图形知识，如绳子和绳子上的结、刻度尺与它上面的刻度，温度计与其上面的刻度，我们每天走过的路线可以看作是一条直线，教室里每个学生的座位等等，我们利用学生的这一认识基础，把生活中的形与数相结合迁移到数学中来，在教学中进行数形结合思想的渗透，挖掘教材提供的机会，把握渗透的契机。如有理数中数轴的引入、不等式及不等式组的解集在数轴上表示，使抽象的概念、性质得到直观的理解；解二元一次方程组、解不等式时，利用平面直角坐标系，通过转化成一次函数图像图解，问题变得简单易懂。统计部分三类统计图应用后即可使啰嗦的语言文字变得简洁明了；用“树形图”分析事件的概率，可使事件简单而明确。学生在画图中整理信息，分析信息，短时间内就找到了解决问题的方法，巧妙地用图形来表达抽象的数学知识，构建出清晰的数学知识体系，促进知识的“消化”。有些繁杂的代数题，若我们借助于图形的性质，可以使许多抽象的概念及复杂的数量关系直观化、简单化，从而探索出巧妙的解法。

二、“以数解形”

许多几何问题仅仅是单纯的图形研究，透过形的外表，已经触及其内在的数量特征，探索由图形到数量的联系与规律，即“以数助形”就是将图形信息转化为代数信息，使要解决的几何问题化为数量关系来实现“数形结合”。在数学问题中，经常会遇到一些探索规律题，在教学中图形规律题的探索也是常见一种形式，遇到这一类问题，我们必须学会分析图形位置与图形本身的联系，将几何图形变化情况进行数字化、代数化，这就是“以数解形”。

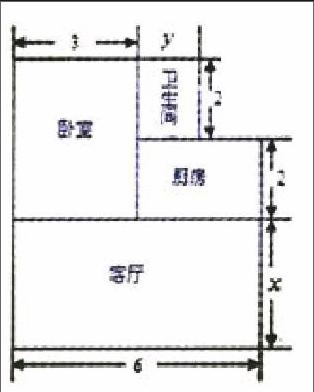
例：小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示。根据图中的数据（单位：m），解答下列问题：

（1）用含x、y的代数式表示地面总面积；

（2）已知客厅面积比卫生间面积多21m²，且地面总面积是卫生间面积的15倍。若铺1m²地砖的平均费用为80元，那么铺地砖的总费用为多少元？

[解析]（1）地面总面积为：6x+2y+18（m²）

（2）根据题意，得

∴地面总面积为：6x+2y+18=45

∴铺地砖的总费用为：45×80=3600（元）。

解题的关键是理解题意，读懂图表。通过对图表中数据信息的分析、比较、判断和归纳，弄清数据间的内在联系，然后利用所学知识（主要是方程（组）、不等式（组）、函数及统计知识），正确建立数学模型解决问题。

总之，通过数与形有机结合，使学生的思维完成从“形象到“抽象”的概括，从“抽象”到“形象”的再现。数学思想方法既是数学基础知识，又是将知识转化为能力的桥梁，用好了就是能力。因此我们数学老师在教学中要注重数学思想方法的渗透、概括和总结，要重视数学思想方法在解题中的应用。

（责任编辑 曾卉）