两类本原有向图的广义scrambling指数

张洁敏，高玉斌



两类本原有向图的广义scrambling指数

张洁敏，*高玉斌

（中北大学理学院，山西，太原 030051）

对两类本原有向图进行研究。结合本原有向图的特点，对图中的每一点经过长途径所到达的点集合进行分析，根据广义scrambling指数定义，得到了这两类本原有向图的广义scrambling指数。

本原有向图；点；途径；广义scrambling指数

2009年，Akelbek M 和Kirkland S根据随机矩阵的第二大特征值，在文献[1]中提出了本原有向图的scrambling指数定义，并在文献[2]中给出了围长为s的本原有向图scrambling指数的上确界，还解决了一般本原有向图的scrambling指数上确界。Akelbek M，Fital S等在文献[3]中利用布尔秩求出本原有向图的scrambling指数的上界。文献[4]研究了一类特殊本原有向图的scrambling指数。2010年，黄宇飞，柳柏濂在文献[5]中将scrambling指数推广到广义scrambling指数，给出了本原有向图的广义scrambling指数定义，并给出了三类本原有向图的广义scrambling指数的确界与极图。文献[6] 研究了2个特殊本原有向图的scrambling指数与广义scrambling指数。

1 预备知识

设为阶有向图（可以有环，但不能有重弧），若存在正整数，使得对任意一对从到都有长为的途径（记），则称为本原有向图，并称满足条件的最小正整数为本原有向图的本原指数，记为。有向图是本原有向图等价于有向图为强连通图，且中所有圈长的最大公因子为1[7]。

对有向图D有如下定义：(D)=()，对有向图D有如下定义：(D)=()

定义1[1]设为阶本原有向图，若存在正整数对任意一对总存在一点使得在中有则称满足条件的最小正整数为的scrambling指数，记为。

定义2[5]设为阶本原有向图，正整数对于集合用来表示最小的正整数使得存在个顶点对于在中都有，则将

分别称为本原有向图的重下–scrambling指数和重上–scrambling指数。当=1时，记称为本原有向图的广义scrambling指数。

引理1[5]设为阶本原有向图，有，。

2 主要结果

定理1 令1为如图1表示的阶本原有向图，则对正整数有

。

；

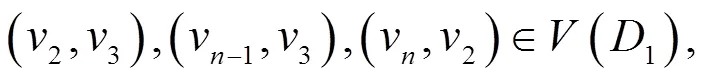
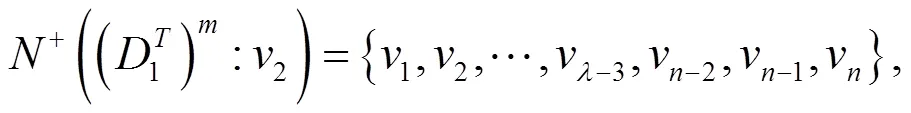
根据引理1可知

。

图2 n阶本原有向图

；

。

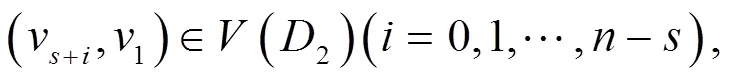
参考文献：

[1] Akelbek M, Kirkland S. Coefficients of ergodicity and the scrambling index [J].Linear Algebra and its Applications, 2009,430(4):1111-1130.

[2] Akelbek M, Kirkland S. Primitive digraphs with the largest scrambling index [J]. LinearAlgebra and its Applications, 2009, 430(4):1099-1110.

[3] Akelbek M, Fital S, Shen J. A bound on the scrambling index of a primitive matrix using Boolean rank [J]. Linear Algebra and its Applications, 2009,431(10):1923-1931.

[5] Huang Yufei, Liu Bolian. Generalized scrambling indices of a primitive digraph [J]. Linear Algebra and its Applications, 2010, 433(11):1798-1808.

[6] 代爱凤,邵燕灵.2个特殊本原有向图的scrambling指数与广义scrambling指数[J].天津师范大学学报:自然科学版, 2012, 32(3):9-12.

[7] Brualdi R A, Ryser H J. Combinatorial Matrix Theory [M]. Cambridge:Cambridge University Press, 1991.

GENERALIZED SCRAMBLING INDICES OF TWO CLASSES OF PRIMITIVE DIGRAPH

ZHANG Jie-min,*GAO Yu-bin

（School of Science, North University of China, Taiyuan,Shanxi 030051, China）

Two classes of primitive digraph are discussed. Combing with the characteristics of the digraph, we analyze the sets formed by the vertexes, which are arrived by every vertex passing a walk of lengthin the digraph. According to the definitions of generalized scrambling indices, we obtain the generalized scrambling indices of two classes of primitive digraph.

primitive digraph; vertex; walk; generalized scrambling indices

1674-8085(2015)01-0030-04

O157.5

A

10.3969/j.issn.1674-8085.2015.01.006

2014-09-24；修改日期：2014-11-20

山西省回国留学人员科研项目（2012-070）

张洁敏(1990-)，女，河南焦作人，硕士生，主要从事组合数学的研究(E-mail:1367356120@qq.com);

*高玉斌(1962-)，男，山东保德人，教授，博士生导师，主要从事组合数学的研究(E-mail:ybgao@nuc.edu.cn).