一种M-FSK信号的能量度量Viterbi软译码算法性能分析
董彬虹 唐 鹏 杜 洋 赵 岩
一种-FSK信号的能量度量Viterbi软译码算法性能分析
董彬虹 唐 鹏*杜 洋 赵 岩
(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)
Viterbi译码算法广泛应用于无线数字通信系统,一般采用比特对数似然信息(LLR)作为译码器的输入。针对-FSK信号,该文提出一种采用信号解调得到的维能量信息,直接作为译码器分支度量值,并给出了相应的Viterbi译码算法。在加性高斯白噪声(AWGN)和瑞利(Rayleigh)衰落信道下对所提算法的BER性能进行了理论推导,得到了闭合表达式。通过仿真验证了理论推导的正确性,与常规Viterbi算法相比,所提算法避免了比特LLR和分支度量值的计算,降低了算法复杂度和减少了信息损失,提高了-FSK信号软解调Viterbi译码算法的BER性能,是一种更适用于工程实现的-FSK信号的Viterbi译码算法。
Viterbi译码;比特对数似然信息;能量度量;多元频移键控;误比特率
1 引言
1955年,文献[1]首先提出了卷积编码技术,与分组码不同,卷积码是由连续输入的信息序列得到连续输出的编码序列。与卷积编码技术相对应的所有译码算法中,Viterbi译码算法[2]是在多数信道下的最优译码算法,其充分利用了码字之间的相关性,提高了编码码字的纠错能力,被广泛地应用于WiMAX[3],无线传感器网络[4],航空[5]和航海[6]等无线数字通信领域。因此一直以来Viterbi译码算法的研究文献层出不穷:文献[7]提出了4D-8PSK-TCM系统下的维特比译码算法,采用一种辅助网格的方法,极大降低了计算路径度量值的运算复杂度;文献[8]提出了一种差分协调信号的Viterbi译码算法,针对差分相移键控(Differential Phase Shift Keying, DPSK)系统,构建了一个基于Viterbi译码接收的三节点差分协同通信系统模型,提高了系统性能;文献[9]对正交相移键控(Quadrature Phase Shift Keying, QPSK)和正交幅度调制(Quadrature Amplitude Modulation, QAM)下使用Viterbi译码的脉冲干扰抑制技术进行研究,结果发现使用基于限制的度量值方法能获得更高的BER性能;文献[10]在高速QPSK解调输出下,提出了一种应用于高速数据接收机下的并行Viterbi译码结构,以此来应对未来数传系统Gbps译码速率的需求。以上文献都是针对相移键控(Phase Shift Keying, PSK)或幅度调制(Amplitude Modulation, AM)信号,其Viterbi译码通常采用输入比特对数似然信息(Log- Likelihood Ratio, LLR)的软判决译码算法[11,12],文献[13]中给出了一种4FSK信号的软解调方法,将软解调后的4维频点能量信号经过降维运算,得到2维的近似比特LLR信息,送入Viterbi译码。
2 M维能量度量Viterbi软译码算法
Viterbi译码主要包括3个单元:分支度量值计算单元,加比选单元和译码回溯单元,PSK, AM信号和文献[13]采用的基于比特LLR软信息输入的Viterbi译码步骤如下:
步骤1 比特LLR软信息计算:在工程中对于PSK和AM信号,由于比特LLR运算量过大,一般采用近似比特LLR算法[14];而对于-FSK信号,文献[13]给出了一种4FSK信号通过降维运算得到比特LLR的方法。
步骤2 分支度量值计算:将步骤1得到的比特LLR软信息与译码状态网格图的输出值逐分支进行欧氏距离计算。
步骤3 加比选单元:将步骤2得到的分支度量值与当前状态的分支度量值之和(初始值为0)进行累加;比较进入同一状态的所有路径的分支度量值之和,保留最小值路径;选取所有状态更新后的分支度量值之和最小的路径,得到此路径对应的状态编号。
步骤4 译码回溯单元:将步骤3得到的状态编号送入回溯单元进行缓存;达到译码深度后,输出译码结果。
本文针对-FSK信号特点,提出一种能量度量Viterbi软译码算法,直接将信号解调的维能量值作为状态网格图的分支度量值,其中维能量值是接收信号通过一组并行的中心频率为,,,的匹配滤波器,再进行平方律检测得到的;而通常Viterbi软译码算法是以欧式距离作为分支度量值。以=4为例,图1为4维能量度量Viterbi译码状态网格图,图中卷积编码约束长度=3,生成多项式为[5 7],分支度量值为4-FSK信号软解调得到的4维能量值,,和。
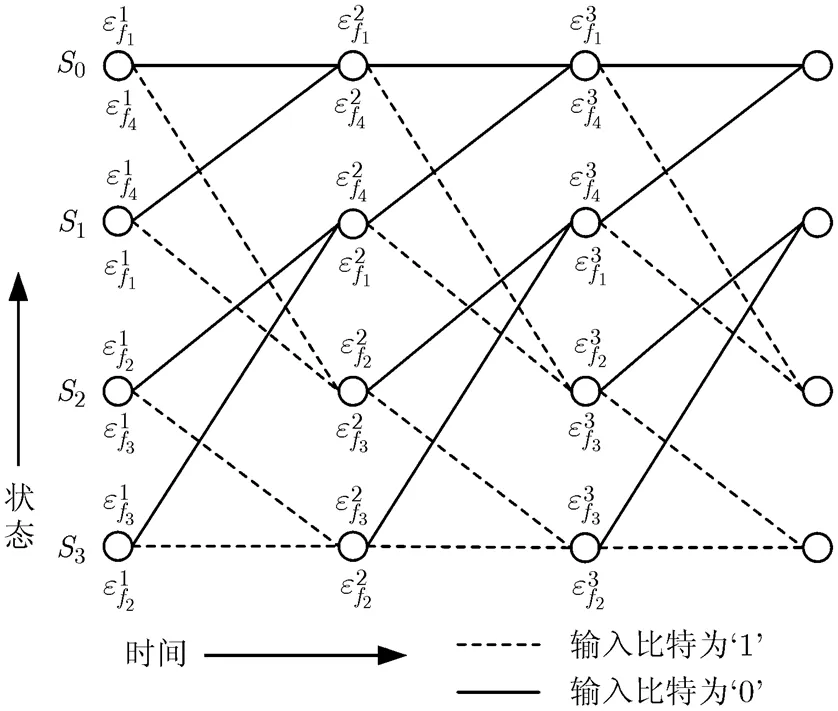
图1 4维Viterbi译码状态栅格图
维能量度量Viterbi软译码算法主要包括两个单元:加比选单元和译码回溯单元,具体步骤如下:
步骤1 加比选单元:将输入的能量分支度量值直接作为分支度量值,并与当前状态的分支度量值之和(初始值为0)进行累加;比较进入同一状态的所有路径的分支度量值之和,保留最大值路径;选取所有状态更新后的分支度量值之和最大的路径,得到此路径对应的状态编号。
步骤2 译码回溯单元:将步骤1得到的状态编号送入回溯单元进行缓存,达到译码深度后,输出译码结果。
对比以上两种Viterbi软译码算法,主要不同之处为:
(1)分支度量值的含义不同:维能量Viterbi软译码算法分支度量值为接收到的维频点能量值,比特LLR输入的Viterbi软译码算法的分支度量值为欧式距离;
(2)加比选的准则不同:维能量Viterbi软译码算法的加比选单元内是选择并保留分支度量值之和最大的路径,比特LLR输入的Viterbi算法在加比选单元内是选择并保留分支度量值之和最小的路径;
(3)算法复杂度不同:维能量Viterbi软译码算法避免了比特LLR和分支度量值的计算,简化了译码器结构,降低了算法复杂度。
此外维能量Viterbi软译码算法相比文献[13]中关于-FSK软解调Viterbi译码算法,由于其避免了计算接收信号比特LLR的信息损失,相应提高了-FSK信号的传输性能;综上所述,本文所提算法更有利于-FSK软解调Viterbi译码的工程实现。
3 接收机模型
-FSK发送信号可以表示为个能量相等、频率不同的正交信号波形,假设发送频率序号为,则相应的信号可以表示为[15]
定义成对比较路径编号为,其中正确路径编号为=0,错误路径编号为=1,表示第条合法频率转移路径上,第时刻信号在第个基带频率的平方包络。成对比较路径上分支度量累加值为
4 BER理论分析
-FSK信号的维Viterbi软译码算法采用基于状态网格序列检测方法,误符号率上界(Symbol Error Rate, SER)可以表示为[15]
4.1 AWGN信道
AWGN信道下,成对比较度量0和1,当1>0发生判决错误:
非中心参数[15],其中为零阶修正贝塞尔函数,可以近似为。
因为符号的接收信号不存在符号间串扰,相互独立,因此正确路径分支度量累加值0的特征函数为
错误路径分支度量累加值1的特征函数为
对特征函数求傅里叶反变换,可得到的概率密度函数为
成对比较度量0和1,当0>1发生判决错误,得成对差错概率为
参照二进制正交信号在个信道上平方律合并的差错概率传输性能的推导,可得到的闭合公式为
4.2 Rayleigh信道
对于Rayleigh信道下,其信道噪声()是方差为的零均值宽带高斯白噪声过程,其中表示单边功率谱密度,表示单边功率谱带宽;是接收信号幅度,随机变量服从瑞利分布,其概率密度函数为
因为每符号信号所经历的衰落是相互独立统计的,不存在符号间串扰,因此正确路径分支度量累加值0的特征函数为
同样,错误路径的分支度量累加值1的特征函数为
对特征函数求傅里叶反变换,可得0的概率密度函数为
1概率密度函数为
成对比较度量0和1,得成对差错概率为
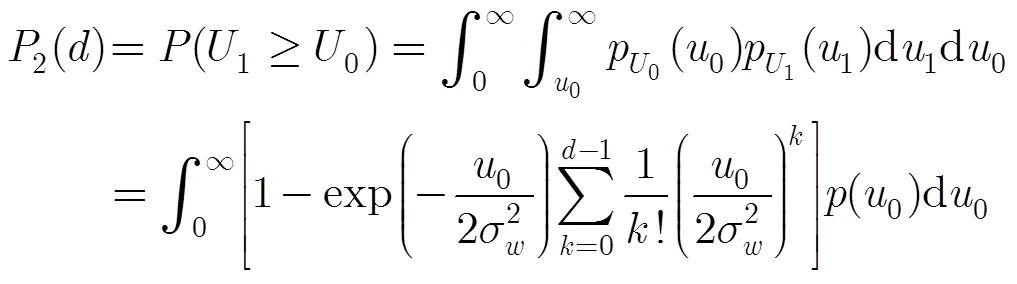
4.3 BER闭合表达式
通过4.1节和4.2节的推导,分别得到了AWGN和Rayleigh信道下,最后将式(15)代入式(5)可以得到-FSK信号在AWGN信道下的SER上界为
而将式(27)代入式(5)就可以得到-FSK信号在Rayleigh信道下的SER上界为
若每个数据符号由个信息比特组成,根据关系式
5 仿真结果
本文中,-FSK信号频率间隔为5 kHz且= 1,量化精度为14 bit,译码深度为64,为保证-FSK信号正交性,设置符号驻留时间μs;经过计算,在AWGN信道中,当式(5)中, Rayleigh信道中,当,基本趋于稳定。因此,下面的理论分析中,对AWGN信道采用=,对Rayleigh信道采用=近似计算,其中是最小自由距离,其余系统参数如表1所示。

表1系统参数
图2和图3分别为AWGN信道和Rayleigh信道下,本文提出的-FSK信号的能量度量Viterbi软译码算法BER性能理论和仿真分析结果。可以看到,理论上界随着信噪比的增加迅速逼近仿真曲线,这是因为式(5)中不同路径的首次差错事件概率重复累加,导致理论界大于仿真结果,但是随着E/0的增大,首次差错事件概率重复累加造成的误差迅速减小,理论上界迅速逼近仿真结果,因此本文对所提算法BER性能理论分析的结果是正确的。
从图2和图3中还可以看到,在AWGN信道或者Rayleigh信道中,当时,从4增加到8,本文提出算法的增益分别增加了0.482 dB和1.257 dB,这是因为本文提出算法最大程度利用FSK软解调输出的频点能量信息进行译码,使Viterbi译码获得了相应的增益,而当继续增加到16,本文提出的算法性能增益变化不大,这是因为在译码过程中,符号的信号非相干合并损失的增加抵消了编码增益。
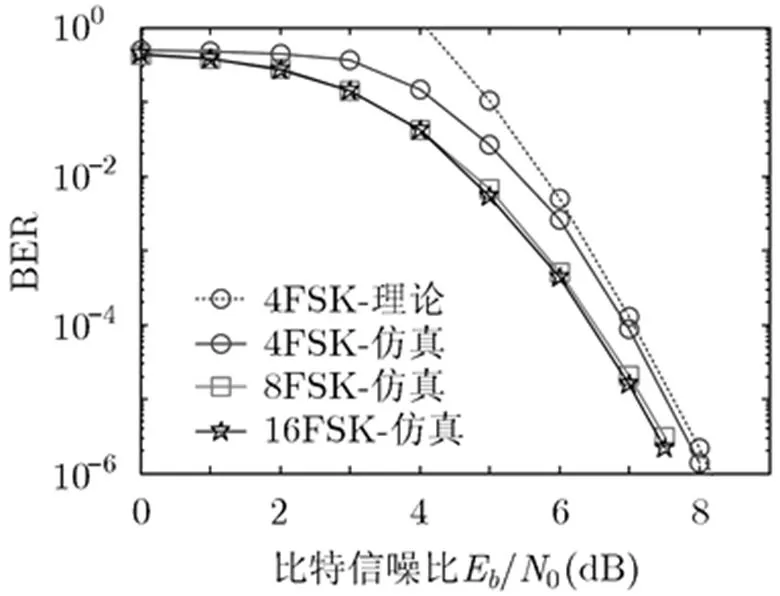
图2 AWGN信道下本文算法理论和仿真性能

图3 Rayleigh信道下本文算法理论和仿真性能
图4和图5分别为4FSK通信系统在AWGN信道和Rayleigh信道下,文献[13]算法与本文算法的BER性能对比。结果表明,当时,在AWGN信道中,本文提出的Viterbi译码算法比文献[13]算法提高了约0.62 dB的信噪比增益;在Rayleigh信道中,提高了约0.67 dB的信噪比增益。这是因为文献[13]算法需要将维能量信息通过降维运算,生成的比特似然信息,值越大,降维后损失的维度也就越大。本文所提算法采用-FSK信号解调和译码器的紧耦合设计,避免了比特LLR计算带来的降维信息损失,因此BER性能得到了提高。
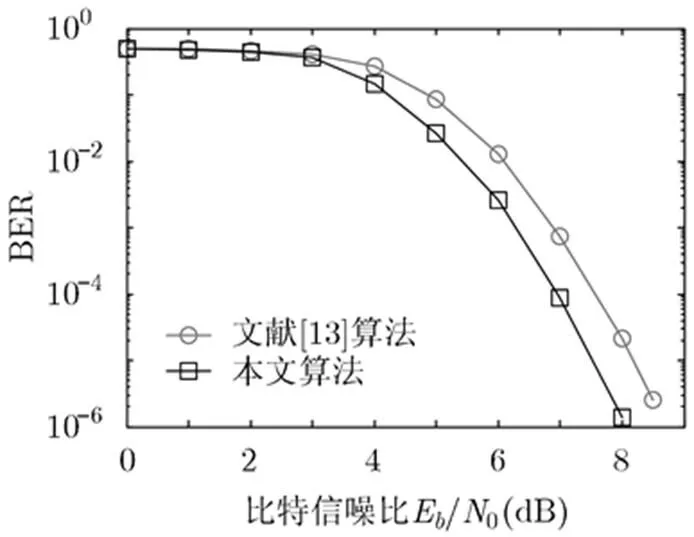
图4 在AWGN信道下文献[13] 与本文算法的性能对比
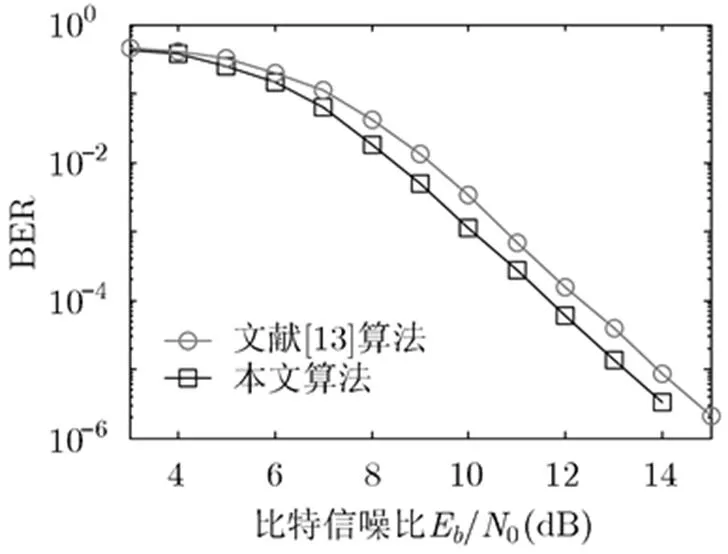
图5 在Rayleigh信道下文献[13]与本文算法的性能对比
5 结束语
为了提高-FSK信号的传输性能,本文提出了一种适用于-FSK信号的维能量度量Viterbi软译码方法,并对-FSK系统在AWGN信道和Rayleigh信道下的性能进行了理论推导,得到了BER的上界闭合表达式,通过仿真验证了理论推导的正确性;对比比特LLR输入的Viterbi译码算法,由于本文所提算法采用-FSK信号解调和译码器的紧耦合设计,避免了比特LLR和分支度量值的计算,减小了复杂度,更利于工程实现。此外,由于避免了文献[13]算法进行比特LLR计算带来的降维信息损失,因此BER性能也得到了提高。
参考文献
[1] Elias P. Coding for noisy channels[C]. 1955IRE Convention Record, 1955: 37-47.
[2] Viterbi A J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm[J]., 1967, 13(2): 260-269.
[3] Kene J D and Kulat K D. WiMAX physical layer optimization by implementing SOVA Decoding algorithm[C]. Proceedings of 2014 International Conference on Circuits, Systems, Communication and Information Technology Applications (CSCITA), Mumbai, India, 2014: 179-183.
[4] Kudeshia A and Jagannatham A K. Optimal viterbi based total variation sequence detection(TVSD) for robust image/video decoding in wireless sensor networks[J]., 2014, 21(6): 722-726.
[5] Chen Tao, Chen Bo, Xu Ding-hai,.. Channel quality estimation with MMSE filter and Viterbi decoding for airborne communications[C]. Proceedings of 2014 Integrated Communications, Navigation and Surveillance Conference (ICNS), Herndon, USA, 2014: 8-10.
[6] Li Yang, Liu Kui-sheng, Tao Ran,.. Adaptive Viterbi- based range-instantaneous doppler algorithm for ISAR imaging ship target at sea[J]., 2014, DOI:10.1109/JOE.2014.2312237.
[7] 黄远达, 熊蔚明, 孙辉先. 采用辅助网格的4D-8PSK-TCM维特比译码[J]. 空间科学学报, 2008, 28(6): 578-583.
Huang Yuan-da, Xiong Wei-ming, and Sun Hui-xian. Auxiliary trellis based Viterbi decoding algorithm research of 4D-8PSK-TCM[J]., 2008, 28(6): 578-583.
[8] 臧国珍, 宋贝, 田冲. 差分协同信号的维特比译码接收[J]. 军事通信技术, 2013, 34(1): 17-20.
Zang Guo-zhen, Song Bei, and Tian Chong. Viterbi decoding for differential cooperative communication[J]., 2013, 34(1): 17-20.
[9] Morishima Y, Oka I, and Ata S. Pulse interference mitigation techniques for QPSK and QAM using Viterbi decoding[C]. Proceedings of 2010 International Symposium on Information Theory and its Applications (ISITA), Taichung, 2010: 639-643.
[10] 罗宁. 一种高速数传接收机的高效维特比译码结构设计[J]. 信息通信, 2013(2): 80-81.
Luo Ning. A high efficient viterbi decoding structure in high data rate receiver[J].&, 2013(2): 80-81.
[11] Saleh T S, Marslan I, and Ei-Tanany M. Simplified LLR-based Viterbi decoder for convolutional codes in symmetric alpha-stable noise[C]. Proceedings of 2012 25th IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), Montreal, Canada, 2012: 1-4.
[12] Hagenauer J and Hoeher P. A Viterbi algorithm with soft-decision outputs and its applications[C]. Proceedings of 1989 IEEE Global Telecommunications Conference and Exhibition Communications Technology for the 1990s and Beyond (GLOBECOM), Dallas, USA, 1989: 1680-1686.
[13] 程郁凡, 裴亚丽, 李少谦. 一种4FSK软解调方法[P]. 中国, 200610020632.X, 2009-3-18.
[14] Viterbi A J. An intuitive justification and a simplified implementation of the MAP decoder for convolution code[J]., 1998, 16(2): 260-264.
[15] Proakis J G and Salehi M. Digital Communications[M]. 5th Edition, New York: McGraw-Hill, 2008: 45-48, 109-110, 491-516.
Performance Analysis of Energy Metrics for Viterbi Soft Decoding Algorithm Based on-FSK Signal
Dong Bin-hong Tang Peng Du Yang Zhao Yan
(,,611731,)
The Viterbi decoding algorithm is widely used in the wireless digital communication system, generally using the bit Log-Likelihood Ratio (LLR) as its input. For an-ary Frequency Shift Keying (-FSK) signal, a corresponding Viterbi decoding algorithm by directly adopting the-dimensions energy information of the signal demodulation as the decoder branch metrics is proposed. This paper analyzes the theoretical performance of the proposed algorithm in the AWGN and the Rayleigh fading channels, and the upper bound for closed-form expressions of the Bit Error Rate (BER) performance are derived. The validity of the theoretical derivation is demonstrated by the simulations. Compared with the existing Viterbi algorithm, the proposed scheme can avoid the computing of the bit LLR and the branch metric, also it can descend the complex of the algorithm and decrease the loss of the information, improve the BER performance in the presence of Viterbi decoding algorithm which based on the-FSK signal soft demodulation. Thus, the proposed scheme is a Viterbi decoding algorithm that is more adaptive to the actual project based on the-FSK signal.
Viterbi decoding; Bit Log-Likelihood Ratio (LLR);Energy metrics;-ary Frequency Shift Keying (-FSK); Bit Error Rate (BER)
TN911.22
A
1009-5896(2015)08-1920-06
10.11999/JEIT141532
唐鹏 454847157@qq.com
2014-12-02收到,2015-03-03改回,2015-06-08网络优先出版
国家自然科学基金(61201126),新世纪优秀人才支持计划(NCET- 11-0058)和四川省青年科技基金(2012JQ0020)资助课题
董彬虹: 女,1972年生,教授,研究方向为无线通信系统的抗干扰技术、差分跳频通信系统关键技术.
唐 鹏: 男,1989年生,硕士,研究方向为无线通信、扩频通信系统关键技术.
杜 洋: 男,1988年生,博士,研究方向为无线通信、差分跳频通信系统关键技术.
赵 岩: 男,1990年生,硕士,研究方向为无线通信、同步与捕获通信系统关键技术.

