基于距离检测的自动识别系统和对海雷达航迹抗差关联算法
齐 林 崔亚奇 熊 伟 王 聪
基于距离检测的自动识别系统和对海雷达航迹抗差关联算法
齐 林*崔亚奇 熊 伟 王 聪
(海军航空工程学院信息融合研究所 烟台 264001)
现有的多传感器航迹抗差关联算法,如基于图像配准技术、基于参照拓扑关系的关联算法,计算流程复杂,难以在工程实践中实时应用。该文结合海面舰船目标航迹分布特点,基于单元平均恒虚警检测原理,提出了适用于自动识别系统(AIS)和雷达航迹数据的可信关联算法,为对海雷达系统误差配准和海战场多传感器信息融合的快速有效实现提供保证。蒙特卡洛仿真结果表明,可信关联算法在海面目标环境下具有较高的关联准确性;算法的平均耗时与现有抗差关联算法相比显著降低;基于航迹可信关联结果完成对雷达的自动标校,将雷达量测数据的平均误差降低了近90%。
对海雷达;抗差关联;自动识别系统;单元平均恒虚警检测;实时性
1 引言
对海雷达自身存在的定位偏差、雷达量测精度、数据处理方法等因素容易造成系统误差的产生。雷达系统误差会造成目标量测数据与目标真实位置间存在较大的偏差,进而导致雷达难以准确地对目标进行定位。在海面局部稳定的2维直角坐标系中,测距系统误差使目标航迹发生整体平移,测角系统误差使目标航迹发生整体旋转。为提高雷达量测的准确性,必须借助一些辅助措施实现对海雷达系统误差的估计和补偿。
民用船舶大部分都安装有船舶自动识别系统(Automatic Identification System, AIS),军用平台通过加装具有静默模式的AIS设备获得的合作船舶位置信息可以认为是目标的真实航迹。利用AIS上报的目标位置信息对雷达量测数据进行校正可以有效提高雷达的量测精度,误差配准的前提是系统误差下AIS与雷达航迹的准确关联。
本文基于海面舰船目标航迹分布特点和单元平均恒虚警检测原理[14]提取海面目标可信航迹关联对,基于可信航迹关联对估计雷达量测数据系统误差,基于误差补偿后的雷达量测实现与AIS航迹的抗差关联。全文内容安排如下:第2节给出AIS与雷达航迹的可信关联流程:包括数据预处理,距离矩阵的求取,可信航迹关联对的定义及提取方法;第3节仿真验证及结果分析,实验证明了本文算法相对于现有算法的优越性能;第4节总结全文。
2 航迹的可信关联流程
通过对大量AIS和对海雷达上报的海面目标航迹数据分析可得,海面目标航迹具有如下特点:(1)航迹分布零散;(2)系统误差对目标航迹造成一定的偏差,但通常情况下仍小于船舶之间的实际距离;(3)海面舰船目标不都安装有AIS设备,非合作目标的AIS位置信息也不可能为我方所知,造成AIS和雷达上报的目标个数不一致。基于上述特点,可以认为系统误差存在的条件下海面上距离较小且附近一定范围内没有其它目标的一对来自不同传感器的航迹源自同一目标,本文将其定义为可信航迹关联对。
2.1 AIS与雷达量测数据的坐标统一
AIS上报的目标位置信息以地理坐标(经度、纬度、高度)的形式表示,雷达对海量测通常在空间极坐标系下完成,并上报极坐标系下的目标位置数据。为实现AIS和雷达数据的航迹关联,首先需要将它们的数据形式统一到以雷达所在位置为原点的海面局部稳定2维直角坐标系中。
AIS上报的目标位置信息以地理坐标表示,假设雷达所在位置的地理坐标为,其中,,分别表示雷达所在位置的经度、纬度、高度;目标所在位置的地理坐标为,这里针对海面目标,默认。本文基于简化的高斯-克吕格投影原理[15],得到AIS上报目标在海面局部平面直角坐标系中的位置为
2.2距离矩阵的建立
要求出雷达与AIS目标航迹之间的距离,需要实现雷达与AIS上报点迹的时间对齐。这里以AIS的点迹时刻为基准,用插值法[16]将雷达的目标位置数据对齐到AIS的目标点迹时刻,得到
2.3可信航迹关联对定义
海面上某对来自不同传感器的目标航迹,如果满足条件:(1)它们是距离彼此最近的航迹,它们的间距小于某个阈值;(2)在它们周围一定范围内没有其他航迹出现,即距离它们次近的航迹与它们之间的距离大于某个阈值;满足上述条件的航迹对即可信航迹关联对。
2.4 基于单元平均恒虚警率(CA-CFAR)检测的可信航迹关联对的提取方法
由于系统误差引起不同的目标发生基本一致的航迹偏差,且通常情况下上述航迹偏差与船舶之间的实际距离相比较小,所以距离矩阵中最小的若干个元素可以看作由系统误差引起的同源航迹间的距离偏差。由于随机误差的存在,可信航迹关联对的航迹偏差不会完全相等,但它们大小相近,且它们与船舶实际距离间存在距离突变。本文基于上述原理及CA-CFAR检测方法求同源航迹距离阈值和非同源航迹距离阈值。将距离矩阵中所有元素按由小到大的顺序放入集合中,,将中相邻元素按序作差放入集合中,。
如图1所示为CA-CFAR检测器原理框图,其中为加权系数;前沿参考滑窗长度为;为恒虚警检测器输入信号,为第个检测统计量;和为与检验统计量相邻的两个保护单元;取自检测统计量前沿的个输入数据的均值;为第个检测统计量对应的恒虚警输出。此时满足

图1平均值类单脉冲恒虚警检测器框图
3 仿真验证及结果分析
3.1可信航迹关联流程仿真
某海域有20批舰船目标,目标初始位置在海域中均匀分布,目标以匀速直线航行,初始速度和初始航向分别在和之间均匀分布。AIS和雷达上报的目标航迹如图2所示,雷达设备系统误差测距、测角,随机误差满足测距,测角的高斯分布。
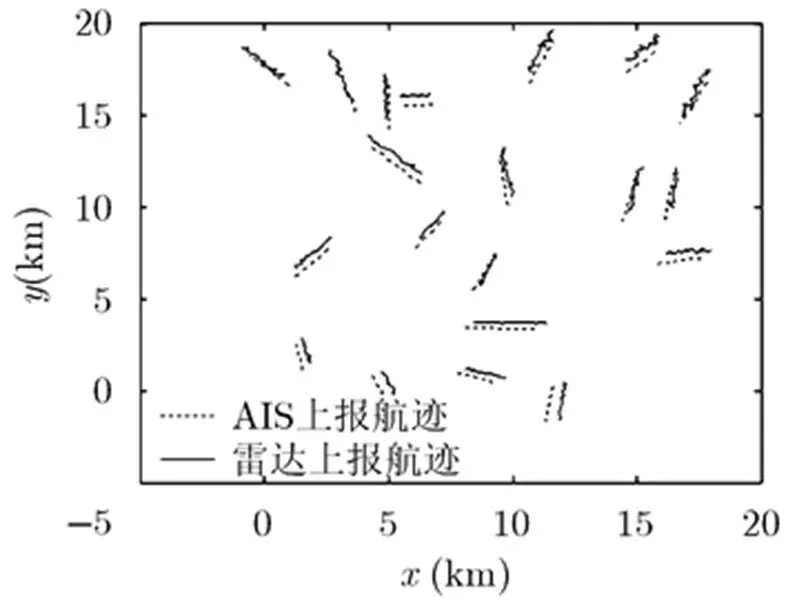
图2 AIS和对海雷达上报的海面舰船目标航迹分布图
分别求出AIS上报航迹与雷达上报航迹之间的距离,组成距离矩阵,这里海面目标批数,则中元素个数。按可信关联算法运算步骤求出集合,,如图3,图4所示,并作为CA-CFAR检测器的输入单元得到输出矢量,如图5所示,按定义求出同源航迹距离阈值,取,得到非同源航迹距离阈值,提取满足要求的可信航迹关联对。基于可信航迹关联对估计系统误差,。对雷达量测数据做误差补偿后海面舰船目标航迹分布如图6所示。

图3 距离矩阵中的元素按序排列

图4距离按序作差

图5 CA-CFAR检测输出矢量

图6 误差补偿后海面舰船目标航迹分布图
3.2算法性能比较与分析
3.2.1目标密集程度对关联性能的影响 对3.1节海面舰船目标仿真环境中的目标个数和系统误差大小做适当修改,对本文提出的基于CA-CFAR原理的可信航迹关联算法与典型的基于图像配准技术的航迹抗差关联算法和基于参照拓扑关系的航迹抗差关联算法进行综合比较与分析。仿真环境具体设置如表1所示。

表1仿真条件参数设置
仿真结果如表2所示,表中列出了在6种环境下,经过50次蒙特卡洛仿真,可信航迹关联算法与图像配准航迹关联算法、目标参照拓扑航迹关联算法的正确、错误、漏关联概率及平均单次耗时。图7为测距系统误差,测角系统误差,海域中目标批数由5增加至30时,各算法平均耗时。这里使用,,分别表示正确、错误、漏关联概率。

图7 算法在不同目标分布密集程度下的平均耗时

表2关联算法性能比较
由表2所示,3种算法都具有较高的正确关联率和较低的错误关联率及漏关联率,说明基于图像配准技术的航迹抗差关联算法,基于目标参照拓扑关系的航迹抗差关联算法及本文提出的可信航迹关联算法在测距误差小于,测角误差为,海域中目标批数小于条件下都具备较高的关联准确性。
结合可信航迹关联算法的特点,比较表2和图7不同环境下算法的平均耗时,分析不同环境条件对算法耗时的影响。比较环境1, 2, 3(或环境4, 5, 6)条件下3种算法的平均耗时,当系统误差不变,海域中目标密集程度逐渐增加时,图像配准关联算法平均耗时基本不变,始终维持在8 s以上。基于目标参照拓扑关系的航迹抗差关联算法平均耗时随着环境中目标密集程度的增大平方增长,当海域中有30批舰船目标时,算法平均耗时达到了近8 s,接近图像配准关联算法;当海域中目标批数为10时,算法平均耗时为0.25 s左右。可信航迹关联算法平均耗时同样随着环境中目标密集程度的增大而增长,但始终保持在低耗时水平,当海域中舰船目标批数增加到30时,算法平均耗时接近0.5 s。
基于图像配准技术的航迹抗差关联算法平均耗时较长,从原理上分析,该算法将海面传感器照射的航迹数据空间做网格化描述,基于一定的数域变换原理(Radon变换)和相位相关技术估计出系统误差造成的航迹数据偏差,确定关联航迹对。由于网格长度的确定与目标密集程度、系统误差大小等环境参数无关,算法计算量基本恒定。但由于算法流程中数域变换需要大量的计算,算法整体耗时较长,不适合实时应用。基于目标参照拓扑关系的航迹抗差关联算法的平均耗时基本不受系统误差大小的影响,但随着环境中目标个数增多平方增长。考虑到目标参照拓扑关联基于目标间的相对位置关系描述目标的拓扑特征,而目标之间互为参照对象,当环境中目标个数增多时,对象周围目标个数增多,计算每个对象的拓扑特征所需的计算量随之增大,而描述所有目标的拓扑特征需要的计算量平方增长。本文提出的可信航迹关联算法随着环境中目标个数增多耗时缓慢增大,由于算法核心步骤基于单元平均恒虚警检测原理的距离阈值提取流程简单,算法整体耗时较短。
3.2.2系统误差大小对关联性能的影响 传感器系统误差大小是衡量关联性能的重要指标,本节在海面目标个数为10个,AIS上报目标个数为5个,测距误差和测角误差如表3所示的条件下综合比较图像匹配关联、目标参照拓扑关联、可信关联3种算法的关联准确性和算法耗时,关联结果如表4所示。如表所示,各算法的运算耗时基本不受系统误差大小的影响,在各自均值周围小幅浮动。基于CA- CFAR检测的可信航迹关联算法展现出计算流程简单,耗时较少的特性,目标参照拓扑关联算法次之,图像匹配关联算法耗时较长,不具备数据实时处理能力。

表3仿真条件参数设置

表4关联算法性能比较
随着仿真环境中系统误差的增大,算法的关联准确性呈现不同的变化趋势。环境1, 2, 3, 4中系统误差较小,3种算法都具备较高的正确关联率,错误关联率和漏关联率很低。环境5, 6, 7, 8中,测距误差增大至2000 m以上,基于目标参照拓扑关系的航迹抗差关联算法的正确关联率有小幅下降,但仍然维持在较高水平。基于图像匹配的航迹抗差关联算法和可信航迹关联算法的正确关联率有明显下降。分析上述结果产生的原因,首先考虑雷达系统误差造成的航迹偏差,如图8所示是雷达系统误差分解图,图中目标真实位置,即AIS上报目标位置信息为

图8 雷达系统误差分解图
由式(17),式(18)可知,系统误差造成的整体航迹图像的平移量大小主要与测距误差及目标方位角有关,当较小时,平移量随方位角变化幅度较小,可以忽略;当取值较大,达到几千米时,平移量随方位角的变化幅度达到千米量级,造成整体航迹图像变形。基于图像匹配原理的航迹抗差关联算法基于数域变换原理寻找使AIS航迹图像和雷达航迹图像匹配最好的平移量和旋转角,由于大的测距误差引起图像中的平移量随方位角大幅变化,甚至造成整体航迹图像变形,当测距误差达到千米以上时算法关联准确性明显降低。
可信航迹关联算法要求系统误差引起的航迹偏差小于目标间的实际距离,基于单元平均恒虚警检测原理可提取出有效的距离阈值,当系统误差引起的航迹偏差过大,算法提取的距离阈值不准确。实际情况下,为确保航行安全,海面上船舶之间要保持一定的距离。海面舰船目标航迹分布零散,系统误差造成的航迹偏差小于目标之间的实际距离的条件通常容易满足,本文提出的基于CA-CFAR原理的可信航迹关联算法具有广泛的应用背景,适宜在工程实践中推广应用。
4 结束语
本文针对AIS和对海雷达信息融合中的航迹实时抗差关联问题提出了基于单元平均恒虚警检测原理的可信航迹关联算法。经仿真验证及结果分析,得到关于算法的如下结论:(1)可信航迹关联算法相对于现有多传感器航迹抗差关联算法的显著优势是运算流程简化、运算时间大幅降低。特别是环境中目标批数较多时(达到30批),基于目标参照拓扑关系的航迹抗差关联算法的平均耗时接近8 s,与基于图像匹配的航迹抗差关联算法接近,已不具备数据实时处理能力,相同条件下可信航迹关联算法平均耗时0.5 s,体现出优越的实时性。(2)可信航迹关联算法在海面目标环境下具有较高的关联准确性和较好的鲁棒性。仿真结果表明,经可信关联及系统误差配准,对海雷达量测误差降低近90%。(3)本文使用误差补偿后的二次关联得到准确的航迹关联关系,也可基于一次可信关联结合2维最优分配方法解决系统误差下海面目标航迹间的抗差关联问题。(4)基于可信关联的对海雷达自动标校技术能大幅降低雷达量测数据的系统误差,快速有效提升雷达跟踪融合系统的准确性;可信关联算法为海战场多传感器信息融合技术提供了一种新思路和新方法。
参考文献
[1] 何友, 王国宏,, 等. 多传感器信息融合及应用(第2版) [M]. 北京: 电子工业出版社, 2007: 128-165.
He You, Wang Guo-hong, Lu Da-jin,. Multisensor Information Fusion with Applications(Second Edition)[M]. Beijing: Publishing House of Electronics Industry, 2007: 128-165.
[2] 何友, 王国宏, 关欣. 信息融合理论与应用[M]. 北京: 电子工业出版社, 2010: 178-238.
He You, Wang Guo-hong, and Guan Xin. Information Fusion Theory with Applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 178-238.
[3] Liu Xi, Yin Hao, Tian Chang,. An improved 2-D assignment algorithm for track-to-track association[C]. 25th Chinese Control and Decision Conference, Guiyang, China, 2013: 3698-3703.
[4] Phani C and Arye N. Concurrent particle filtering and data association using game theory for tracking multiple maneuvering targets[J]., 2013, 61(20): 4934-4948.
[5] 何友, 宋强, 熊伟. 基于相位相关的目标航迹对准关联技术[J]. 电子学报, 2010, 38(12): 2718-2723.
He You, Song Qiang, and Xiong Wei. Track alignment- correlation technique based on phase correlation[J]., 2010, 38(12): 2718-2723.
[6] 何友, 宋强, 熊伟. 基于傅里叶变换的航迹对准关联算法[J]. 航空学报, 2010, 31(2): 356-362.
He You, Song Qiang, and Xiong Wei. A track registration- correlation algorithm based on fourier transform[J]., 2010, 31(2): 356-362.
[7] 宋强, 熊伟, 何友. 基于复数域拓扑描述的航迹对准关联算法[J]. 宇航学报, 2011, 32(3): 560-566.
Song Qiang, Xiong Wei, and He You. A track alignment- correlation algorithm based on topological description of complex number field[J]., 2011, 32(3): 560-566.
[8] Tian Wei, Wang Yue, Shan Xiu-ming,. Track-to-track association for biased data based on the reference topology feature[J]., 2014, 21(4): 449-453.
[9] Tian Wei, Wang Yue, Shan Xiu-ming,. Analytic performance prediction of track-to-track association with biased data in multi-sensor multi-target tracking scenarios[J]., 2013, 13(9): 12244-12265.
[10] 田威, 王钺, 山秀明, 等. 稳健的联合航迹关联与系统误差估计[J]. 清华大学学报(自然科学版), 2013, 53(7): 946-950.
Tian Wei, Wang Yue, Shan Xiu-ming,. Robust method for joint track association and sensor bias estimation[J].(), 2013, 53(7): 946-950.
[11] 石玥, 王钺, 王树刚, 等. 基于目标参照拓扑的模糊航迹关联方法[J]. 国防科技大学学报, 2006, 28(4): 105-109.
Shi Yue, Wang Yue, Wang Shu-gang,. Fuzzy data association based on target topology of reference[J]., 2006, 28(4): 105-109.
[12] 杨哲, 韩崇昭, 李晨, 等. 基于目标之间拓扑信息的数据关联方法[J]. 系统仿真学报, 2008, 20(9): 2357-2360.
Yang Zhe, Han Chong-zhao, Li Chen,. Data association based on target topology[J]., 2008, 20(9): 2357-2360.
[13] 吴泽民, 任姝婕, 刘熹. 基于拓扑序列法的航迹关联算法[J]. 航空学报, 2009, 30(10): 1937-1942.
Wu Ze-min, Ren Shu-jie, and Liu Xi. Topology sequence based track correlation algorithm[J]., 2009, 30(10): 1937-1942.
[14] 何友, 关键, 孟祥伟, 等. 雷达目标检测与恒虚警处理(第2版)[M]. 北京: 清华大学出版社, 2011: 36-53.
He You, Guan Jian, Meng Xiang-wei,. Radar Target Detection and CFAR Processing(Second Edition)[M]. Beijing: Tsinghua University Press, 2011: 36-53.
[15] 徐志京, 王解先. AIS与雷达目标信息融合中坐标位置的计算方法[J]. 上海海事大学学报, 2005, 26(4): 78-81.
Xu Zhi-jing and Wang Jie-xian. Numerical method to calculate coordinate transformation between AIS and radar object for information fusion[J]., 2005, 26(4): 78-81.
[16] Mathews J H and Fink K D著. 周璐, 陈渝, 钱芳, 等译. 数值方法(MATLAB版, 第4版)[M]. 北京: 电子工业出版社, 2010: 195-202.
Anti-bias Association Algorithm for Automatic Identification System and Radar Based on Bias Detection
Qi Lin Cui Ya-qi Xiong Wei Wang Cong
(,,264001,)
The classical multi-sensor anti-bias association algorithms require complex calculation procedure, can not be used in real-time condition, for instance the algorithms based on image matching and reference topology feature. On the basis of tracks distribution feature on sea surface and Cell-Average Constant False Alarm Rate (CA-CFAR) detection theory, a real-time anti-bias association algorithm for Automatic Identification System (AIS) and the data track of radar is proposed, named confidential-association algorithm, to make real-time radar systematic error registration and multi-sensor information fusion come true. Monte-Carlo simulation results show that the accuracy of confidential-association algorithm maintains on a high level on the sea-surface environment, it has the superiority of simply calculation procedure and substantially reduces run-time in comparison to current anti-bias association algorithms. Radar automatically registration technique based on confidential-association algorithm reduces average error of the measured data by nearly 90%.
Radar for sea; Anti-bias association; Automatic Identification System (AIS); Cell-Average Constant False Alarm Rate (CA-CFAR) detection; Real-time
TN953; TN957
A
1009-5896(2015)08-1855-07
10.11999/JEIT141472
齐林 3278pirate@163.com
2014-11-24收到,2015-04-10改回,2015-06-09网络优先出版
山东省自然科学基金青年基金(ZR2012FQ004)和飞行器测控与通信教育部重点实验室开放基金(CTTC-FX201302)资助课题
齐 林: 男,1989年生,博士生,研究方向为多传感器信息融合.
崔亚奇: 男,1987年生,博士,讲师,研究方向为误差配准、状态估计融合.
熊 伟: 男,1977年生,博士,教授,研究方向为多传感器信息融合、指挥自动化.
王 聪: 男,1989年生,博士生,研究方向为多目标跟踪、信息融合.

