记忆阻尼力作用下非相对论吸积盘的随机共振
汪志云,陈培杰
记忆阻尼力作用下非相对论吸积盘的随机共振
汪志云,陈培杰
(湖北文理学院物理与电子工程学院,湖北襄阳441053)
采用受记忆阻尼力和色关联随机力作用下的广义朗之万方程描述黑洞吸积盘的垂向振荡,用拉普拉斯变换的方法推导得到吸积盘随机振荡的光度和功率密度谱,并分析阻尼力的记忆时间和吸积盘系统参数对功率谱曲线的影响. 研究结果表明:随着阻尼力记忆时间的增大,功率谱()随频率的变化从单调减小到出现极大值,曲线上出现了单峰和多峰的随机共振现象.粘滞系数、吸积率和中心黑洞的质量对曲线上共振峰的强度和位置都有较大的影响.
记忆阻尼力;广义朗之万方程;吸积盘;功率密度谱;随机共振
在天体物理中,包围致密天体的吸积盘已经成为解释许多天文观测现象的一个标准模型,吸积盘作为类星体和黑洞双星系统等致密天体高能辐射的主要能源已被广泛接受[1-2].近来年,随机力作用下的吸积盘振荡引起了越来越多的关注,其研究理论也在不断完善,并成功地解释了一些天体的光变特性[3-9].如Harko 和 Mocanu等用数值模拟方法,推导出广义相对论框架下超大质量黑洞吸积盘垂向振荡光度,并分析了功率密度谱随频率变化[4];Leung 等研究发现Blacc天体24小时内的光度变化与吸积盘的随机振荡有关[5]. 这些研究均采用一个广义朗之万方程来描述吸积盘的振荡.基于此模型,我们分析了在相对论和非相对论两种框架下吸积盘随机振荡光度的功率密度谱,并讨论了功率密度谱曲线上的随机共振现象,解释黑洞双星X射线的低频准周期振荡[6-8]. 然而这些模型并不能解释高频准周期振荡,因为其共振频率是小于1的,并且所采用朗之万方程中的阻尼力是固定不变的.最近研究表明,阻尼力的记忆因素对于吸积盘的动力学行为有较大的影响[9-10]. 本文主要工作是在Leung等人在文献[10]提出的模型基础上,用考虑记忆阻尼力和色关联随机力共同作用的广义朗之万方程描述黑洞吸积盘垂向随机振荡,并用拉普拉斯变换方法从理论上计算其振荡光度的功率密度谱,讨论系统参数对功率谱曲线的影响,分析其共振现象.
1 记忆阻尼力和随机力作用下吸积盘振荡的功率密度谱
考虑包围一黑洞或中子星的标准吸积薄盘,将吸积盘作为整体,受记忆阻尼力和随机力作用产生振荡,其垂向振荡可以用一广义的朗之万方程描述[5]:
式(1)中,是盘的垂向振荡位移,且随时间变量和发生变化;是由黑洞双星系统决定的常量;M是吸积盘质量;阻尼核函数()的表示式为:
式(2)中,是阻尼力的强度,表示吸积盘能量耗散的强度;是阻尼力记忆时间. 式(1)中,()是与记忆阻尼力有关联的随机力,其平均值和在不同时间和的关联满足以下
式(3)中,是决定随机力作用大小的常量.
式(4)中,()满足统计性质为,.
假设0时吸积盘垂向振荡的位移和速度分别为. 通过拉普拉斯变换,可以求解方程(4),并得到吸积盘在任意时刻的位移、速度和加速度分别为:

式中,1、A和3是由初始条件和系统参数所决定的积分常量,G1、G2和0是代数方程的3个根.
吸积盘垂向振荡的总能量可以表示为
由于存在粘滞耗散和随机力的作用,吸积盘的能量会损失.用单位时间内损失的能量表示吸积盘的振荡光度,则有
那么可以得到吸积盘振荡平均光度的自关联函数为

由以上推导可知,要得到受阻尼力和随机力作用下吸积盘的功率密度谱,必须知道吸积盘的质量、阻尼强度等物理量.对于一个包围黑洞的流体吸积标准薄盘,其质量可表示为[11-12]:
式中,R和R分别表示吸积盘的最内边缘半径和外半径,R是调整半径,是面密度指数.S和S0分别表示吸积盘内部和边界层的面密度.令R=3R,r=R/R,r=R/R,=/M,其中表示引力半径,和分别为引力常量和光速. 则[12],、分别为粘滞系数和以临界吸积为单位的吸积率. 根据文献[5],吸积盘振荡阻尼力的强度和频率分别为:
2 吸积盘振荡光度功率密度谱的随机共振
通过以上分析发现,当系统的物理参数选取一定值时,可以通过拉普拉斯变换方法求解吸积盘垂向振荡的位移、速度和加速度,得到振荡光度的功率密度谱(). 因此,将所有参量都采用无量纲量,并假设吸积盘面密度指数=3/5,调整半径为R=3R、外半径为R=104R,可求解式(8)即得到功率密度谱()随谱频率变化关系.下面讨论各系统参数对功率密度谱曲线上随机共振现象的影响.
2.1 阻尼力记忆时间τ对功率密度谱的影响
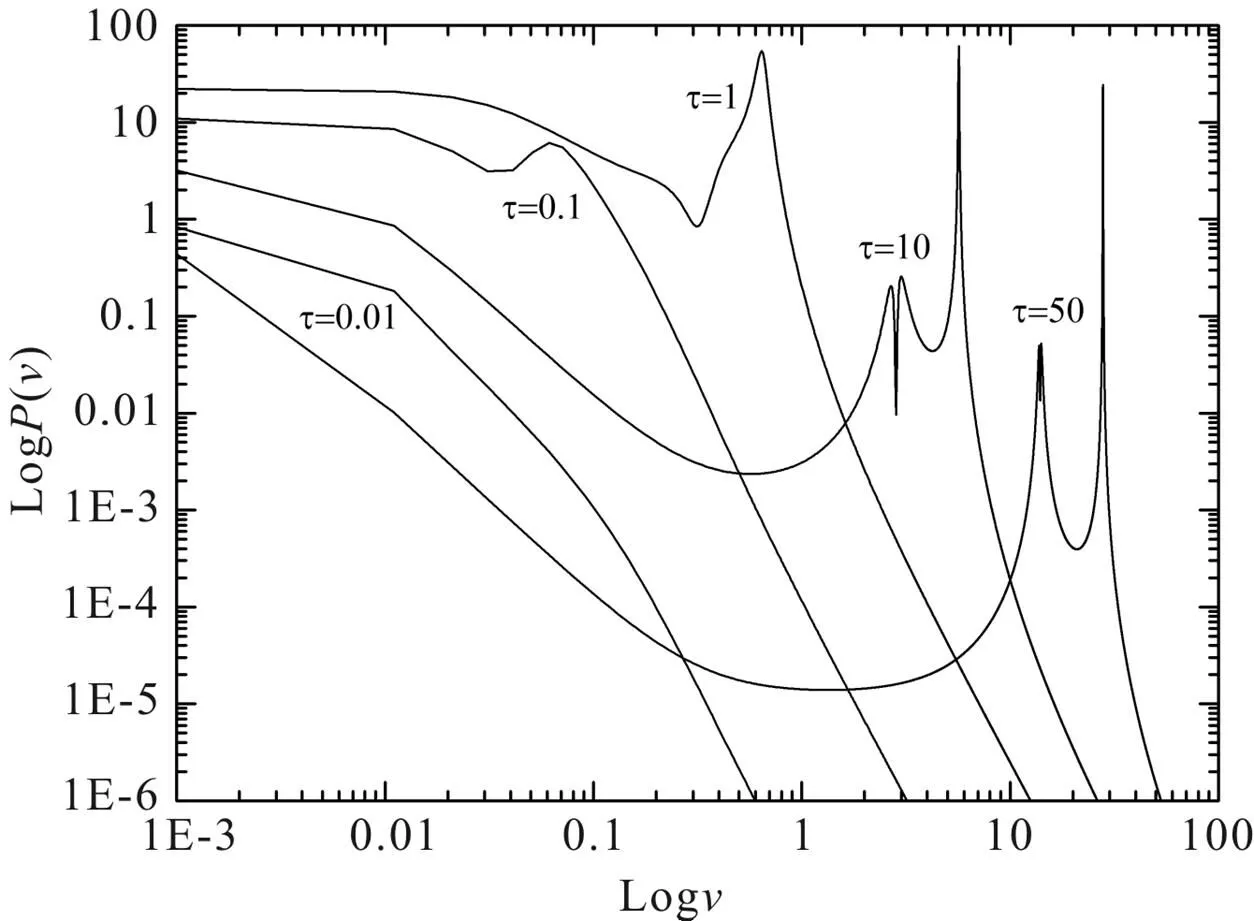
当阻尼核函数的记忆时间τ取不同值时,吸积盘振荡光度的功率密度谱曲线如图1所示. 可以看出:功率密度谱随频率的变化曲线出现一截断,将其大致分为斜率不相同的两部分,且当τ取不同值时,曲线上出现了不同数量的极大值,即出现了不同类型的随机共振现象. 当τ取值较小(τ =0.01)时,(ν)随谱频率ν单调减小,并没有出现极值,即无共振现象;当τ取值从0.1到1之间时,曲线不再是单调变化,而是出现了一个极大值,这是典型的随机共振现象. 随着τ的增大,共振峰越来越尖锐,共振频率越来越大,共振现象更加明显;当τ =10时,曲线上出现了3个共振峰,此为多峰随机共振. 最高共振频率对应的共振峰相比较另外两个共振峰,峰值更高,更尖锐,而较低频率对应的两个共振峰靠得很近,高度几乎相同,中间形成一个共振谷;而当τ =50时,共振峰的数量却减小到两个,形成双峰共振. 随着记忆时间的延长,系统的共振现象更加明显,共振峰的位置向谱频率增大的方向移动,即共振频率增大.
注:
图1不同记忆时间阻尼力作用下吸积盘随机振荡光度的功率密度谱
以上现象说明阻尼力的记忆时间对吸积盘振荡光度功率密度谱的共振现象具有十分重要的影响,相比较固定阻尼作用下的情况[8],产生的共振行为更加丰富,即产生多峰共振. 可以解释为阻尼力的延迟记忆使更多的随机力所做功转换成粘滞耗散的能量,光度增强,共振现象更容易发生.
2.2 吸积盘的粘滞系数和吸积率对功率密度谱的影响
图2表示的是产生阻尼力的粘滞系数和吸积盘的吸积率取不同值时,吸积盘振荡光度的功率密度谱曲线. 可以清晰地看到:和对)~ν曲线的影响是完全相同的. 当它们取值较小时,曲线上现三个极大值,其特征如图1所示一致;随着的增大,低频对应的两个共振峰不断靠拢,且两峰之间的共振谷位置不但上升,使两峰最后合并成一个共振峰,形成双峰共振;(ν)~ν曲线随和的增大而上升,但共振现象减弱,共振峰的位置向频率增大的方向移动.
从式(2)、(3)和(9)可以发现,粘滞系数和吸积率取值较大时,吸积盘边界层的面密度S0减小,吸积盘的质量越小,系统的固有频率越大,则共振峰所对应的频率(共振频率)越高,这与固定阻尼作用下的情况(和不影响共振峰的位置[8])是不相同的. 另外,由式(6)和(7)可以发现,吸积盘质量的减小,导致吸积盘垂向振荡的能量与光度都降低,使随机共振现象减弱.

注:(a)(b)
图2粘滞系数和吸积率取不同值时吸积盘随机振荡光度的功率密度谱
2.3 中心黑洞的质量对功率密度谱的影响
为了讨论黑洞双星系统参数对功率密度谱的影响,图3表示中心黑洞的质量取不同值时吸积盘振荡光度的功率密度谱. 这组曲线显示出与前面相同的双峰或三峰共振现象. 黑洞质量对低频率部分(<0.2)对应的曲线没有影响;当黑洞质量越大时,共振现象更加明显;随着黑洞质量的减小,由三峰共振演变成为双峰共振,峰值更高,且共振峰的位置却向频率增大的方向移动. 由式(10)可知,黑洞的质量主要影响吸积盘振荡的固有频率,质量越大,固有频率越小,所以共振频率也就越小.

注:
图3 黑洞质量取不同值时吸积盘随机振荡光度的功率密度谱
3 结语
本文用一个受记忆阻尼力和随机力作用下的广义朗之万方程表示吸积盘系统垂向振荡,用拉普拉斯变换的方法求解振荡的位移和速度,并求出其振荡光度的功率密度谱. 通过讨论不同参数对功率谱的影响可以发现:功率密度谱随谱频率的变化出现两种不同形式的随机共振现象,当阻尼力记忆时间较短时,功率密度谱随频率单调减小,而随着记忆时间的延长,(ν)~ν曲线上出现了极大值,且其数量也由一个增加到三个,而后又减小到两个,即存在单峰和多峰随机共振现象. 系统的粘滞系数和吸积率对功率密度谱曲线的影响是相同. 而中心黑洞的质量因为决定了吸积盘垂向振荡的固有频率,所以其主要影响随机共振的频率,质量越小,共振频率越大,这与实际观测的黑洞双星系统X射线光变曲线的高频准周期振荡频率与质量成比的关系相一致.
相对于文献[8]所讨论的固定阻尼力作用下吸积盘振荡光度的功率密度谱,曲线上不仅出现了双峰共振,而且其共振频率也增加到几十赫兹,这与观测到黑洞双星系统高频准周期振荡(HFQPOs)相似.因此,考虑记忆阻尼力作用下的吸积盘模型可以作为解释黑洞双星系统的光变特性的理论依据.
[1] REMILLARD R A, MCCLINTOC J E. X-Ray properties of black-hole binaries[J]. AA&A, 2006, 44(1): 49-92.
[2] MCCLINTOC J E, REMILLARD R A. Black hole binaries[M]. Cambridge: Cambridge Univ. Press, 2006.
[3] IOANNOU P J, KAKOURIS A. Stochastic dynamics of keplerian accretion disks[J]. The Astrophysical Journal, 2001, 550(4): 931-943.
[4] HARKO T, MOCANU G. Stochastic oscillations of general relativistic discs[J]. MNRAS, 2012, 421(4): 3102-3110.
[5] LEUNG C S, WEI J Y, HARKO T, et al. Modeling the IDV emissions of the BL Lac objects with a Langevin type stochastic differential equation[J]. J. Astrophys. Astron., 2011, 32(1-2): 189-192.
[6] WANG Z Y, CHEN P J, WANG D X, et al. Stochastic resonance of accretion disk and the persistent low-frequency quasi-periodic oscillations in black hole X-ray binaries[J]. J. Astrophys. Astron., 2013, 34(1): 33-40.
[7] WANG Zhiyun, CHEN Peijie, ZHANG Liangying. Stochastic resonance of a general relativistic accretion disk[J]. CHIN. PHYS. LETT., 2013, 30(9):099801-1-4.
[8] 陈培杰, 蒋亚玲, 汪志云. 色关联随机力作用下吸积盘振荡光度的功率密度谱[J]. 湖北文理学院学报, 2015, 36(2): 5-8.
[9] HARKO T, LEUNG C S, MOCANU G. Generalized Langevin equation with colored noise description of the stochastic oscillations of accretion disks[J].The European Physical Journal C, 2014, 74(5): 2900-1-16.
[10] LEUNG C S, MOCANU G, HARKO T. Generalized Langevin equation description of the stochastic oscillations of general relativistic disks[J]. J.Astrophys. Astron., 2014, 35(3): 449-452.
[11] TITARCHUK L, OSHEROVICH V. The Global Normal Disk Oscillations and the Persistent Low-Frequency Quasi-periodic Oscillations in X-Ray Binaries[J]. The Astrophysical Journal, 2000, 542(2): L111-L114.
[12] SHAKURA N I, SUNYAEV R A. Black holes in binary systems: Observational appearance[J]. A&A, 1973, 24: 337 – 355.
Stochastic Resonance of Non-relativistic Accretion Disks Driven by a Memory-Damped Friction
WANG Zhiyun, CHEN Peijie
(School of Physics and Electronic Engineering, Hubei University of Arts and Science, Xiangyang 441053, China)
By using a generalized Langevin equation to describe the vertical oscillations of a non-relativistic disk subjected to a memory-damped friction and a stochastic force, we derive the power spectrum density (()) of accretion disk oscillating luminosity by the method of Laplace transform, and discuss the influence of system parameters on the() curves. The results show that as the memory timeof the friction increase, the variation of() with spectrum frequencyfrom monotonous decreasing to occur maximums, and the phenomenon of a general stochastic resonance with single-peak and multi-peaks can be found in() curves. The viscidity coefficient, mass accretion rate and the massof black hole have significant influences on the SR phenomena in system of black hole binaries.
Memory-damped friction; Generalized Langevin equation; Accretion disk; Power spectrum density; Stochastic resonance
(责任编辑:饶 超)
P145. 8
A
2095-4476(2015)08-0005-05
2015-03-12;
2015-05-15
湖北省教育厅重点研究项目(D20132603)
汪志云(1973-), 男, 湖北浠水人, 湖北文理学院物理与电子工程学院副教授

