密度核估计的广义相合性

王 敏，李开灿



密度核估计的广义相合性

王 敏，李开灿*

(湖北师范学院数学与统计学院，湖北黄石 435002)

研究独立样本下密度核估计的相合性. 在-2距离和-距离意义下，提出密度核估计广义相合性的概念，并获得密度核估计的各种广义相合性.

-2距离；-距离；密度核估计；广义相合性

密度核估计由和提出，并已成为密度估计的主要方法，其相合性也已得到广泛深入的研究，如文献[1—3]等，但这些研究都是在常见传统距离(如绝对距离)意义下进行的.-2距离和-距离虽然不具备传统距离的对称性，但有非负性和重合性等性质(详见文献[4, 5])，已越来越多地被统计学家接受并应用到统计上，如文献[6—8]等. 但是很少有文献对在-2距离和-距离意义及独立样本下的密度核估计相合性进行研究，因此本文打算讨论这一问题.

1 相关概念及其引理

本文按文献[3]的记号来描述密度函数核估计的概念.

假设1,2, …,n是来自未知密度函数()的独立同分布样本，(×)为¢上的概率密度函数，h>0是一个同有关的常数，定义

为总体未知密度()的一个核估计. 其中(×)为核函数，h为窗宽. 众所周知当(×)为密度函数时，f()也是密度函数. 并且f()是()的无偏估计.

另外，若T()是未知密度函数()的一个估计，如果对固定的有，则称T()为()(在处)的均方相合估计，通常简记为.

为了讨论独立样本下密度核估计的广义相合性，下面定义-2距离和-距离.

设随机变量的密度函数为()，的密度函数为(). 如果，记

称之为密度函数()到()的-2距离.

若()>0，()>0，，则称之为密度函数()到()的-距离，记

引理1[3]设(×)及(×)均为¢上的可测函数，若它们满足条件：1)(×)有界；2)；3)或(×)有界；4). 又常数序列h满足，令，则. 其中"Î()，()表示(×)的连续点集.

引理2[3]设f()是总体未知密度()的一个核估计，即，则有

引理3[3]设核函数(×)为上的密度函数，且满足引理1条件1)和2)，其窗宽满足，则

其中()表示(×)的连续点集合. 若()一致连续，则式(6)关于一致成立.

引理4[3]设核函数(×)是上的概率密度且有界，，，，则f()Þ()，.

2 密度核估计的-2和相合性

事实上，如果核函数(×)是密度函数，则Ef()也是密度函数. 由引理2知，显然Ef()≥0. 又，. 则由定理知

定义1 设T()是未知密度函数()的一个估计，若

则称T()是()的Ⅰ型-2相合估计.

定理1 设1,2, …,n是抽自未知密度函数()的一个简单随机样本，f()是由式(1)定义的核估计，且核函数(×)和密度函数()满足引理3条件，则f()是()的Ⅰ型-2相合估计

证明：由-2距离定义知，，所以

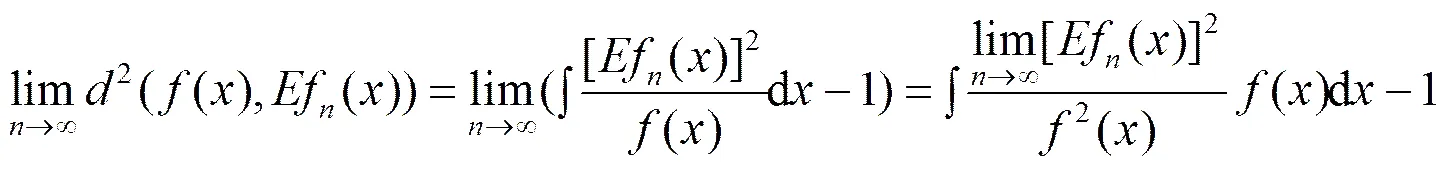
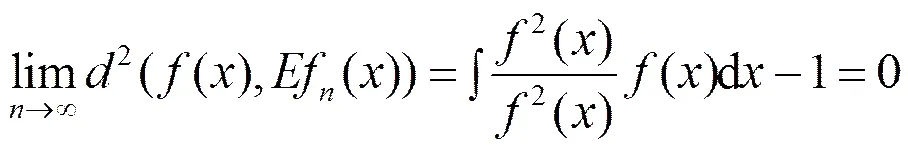
由定义1知f()是()的Ⅰ型-2相合估计.

定义2 设T()是未知密度函数()的一个估计，若

则称T()是()的Ⅰ型-相合估计.

定理2设在定理1的条件下，f()是()的Ⅰ型-相合估计.

证明：由-距离定义知，

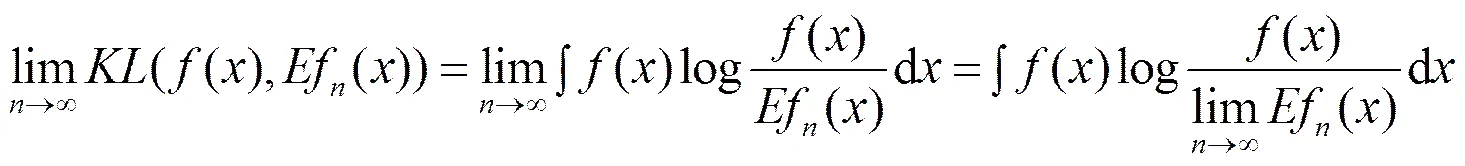
定义3设T()是未知密度函数()的一个估计，若

则称T()是()的Ⅱ型-2相合估计.

定理3 若f()是由(1)式定义的核估计，其中核函数和密度函数()满足一致连续，且当时，，则f()是()的Ⅱ型-2相合估计.

证明：由-2距离定义知. 所以，由定理知.

定理4 设核函数(×)是上的概率密度且有界，，，，则f()是()的Ⅱ型-2相合.

证明：若()，()是密度函数，则

由定义1已知，当(×)是上的概率密度时，f()也是密度，和定理可得

又因为核函数(×)是上的概率密度且有界，，，由引理4知，则.

故f()是()的Ⅱ型-2相合. 由定理4可以得到下面推论：

推论如果密度核估计f()是()的均方相合估计，那么f()是()的Ⅱ型-2相合.

[1] PARZEN EMANUEL. On estimation of a probability density function and mode[J]. The Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.

[2] 陈希孺, 方兆本, 李国英, 等. 非参数统计[M]. 上海: 上海科技技术出版社, 1989.

[3] 陈希孺, 柴根象. 非参数统计教程[M]. 上海: 华东师范大学出版社, 1993.

[4] 李开灿. Peason-c2距离的若干性质[J]. 数学的认识与实践, 2003, 33(1): 49-53.

[5] 蔡择林, 李开灿. 常见分布的最大Kullback-Leibler距离[J]. 武汉大学学报: 理学版, 2007, 53(5): 513-517.

[6] ROBERTS G O, SAHU S K. Updating schemes, correlation structure, blocking and parameterization for the Gibbs Sampler[J]. Journal of the Royal Statistical Society: Series B, 1997, 59(2): 291-317.

[7] LIU S J, WANG W H, KONG A. Correlation structure and convergence rate of the Gibbs Sampler with various scans[J]. Journal of the Royal Statistical Society: Series B, 1995, 57: 157-169.

[8] REISS R D. Approximate Distributions of Order Statistics: With Applications to Nonparametric Statistics[M]. New York: Springer-Verlag, 1980.

Generalized Consistency for Kernel Density Estimation

WANG Min, LI Kaican

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

In this paper, we discuss the consistency of the density kernel estimation under the independent sample. We give the definitions of generalized consistency for kernel density estimation and obtain several kinds of generalized consistency of kernel density estimation under the-2distance and the-distance.

-2distance;-distance; Density kernel estimation; Generalized consistency

O212.7

A

2095-4476(2015)11-0019-04

2015-09-06;

2015-10-15

湖北省教育厅重点项目(D20112503)

王 敏(1992— ), 女, 湖北黄梅人, 湖北师范学院数学与统计学院硕士研究生.

李开灿(1962— ), 男, 湖北武汉人, 湖北师范学院数学与统计学院教授, 主要研究方向: 多元统计分析.

(责任编辑：饶 超)