软弱围岩下浅埋隧道稳定性的能量分析

陈洪林, 吴卫, 树新文



软弱围岩下浅埋隧道稳定性的能量分析

陈洪林, 吴卫, 树新文

(湖南省永龙高速公路建设开发有限公司, 湖南永顺, 416700)

基于能量的角度, 采用极限分析理论中的上限定理对软弱围岩下浅埋隧道的稳定性进行分析, 得到了围岩压力的理论公式。研究表明: 埋深、土体容重越大及黏聚力、内摩擦角越小, 浅埋隧道的围岩压力越大, 破坏范围也越大; 当埋深较大、围岩较好时, 浅埋隧道由于自稳能力有可能不会发生破坏, 而对于比较差的围岩, 在施工过程中应采取更为安全可靠的支护措施, 以防止发生垮塌破坏。

浅埋隧道; 软弱围岩; 极限分析上限法; 围岩压力; 破坏范围

随着我国经济的快速发展, 人们生活水平的提高, 人们对于交通的快捷与便利的要求也随之提高, 从而高速铁路与地下铁道等交通工程得到迅速发展。隧道作为一种重要的地下构筑物, 在高速铁路及城市轨道交通中成为必不可少的组成部分。隧道比较容易发生破坏, 其稳定性问题成为一个热点和难点问题[1–5]。对于浅埋隧道, 由于覆土厚度较小, 围岩的自稳能力相对较差, 在施工过程中容易发生较大的变形, 从而引发隧道塌方等事故[6–8]。目前在我国实际工程中, 对于浅埋隧道的稳定性计算大多采用极限平衡理论。极限分析理论运用于边坡稳定性等岩土工程中, 与极限平衡法等方法相比, 其计算得到的结果更加精确。许多学者将极限分析理论运用于隧道工程稳定性问题研究中, 如文献[9–15]分析了各种不利因素对隧道掌子面稳定性的影响。还有一些学者运用极限分析理论的上限定理对隧道顶部围岩稳定性问题进行了分析[16–20]。本文基于Mohr-Coulomb准则, 构建了一种刚性块体的破坏模式, 采用极限分析法的上限理论对软弱围岩下浅埋隧道的稳定性进行能量分析, 并讨论各个参数的变化及软弱围岩对于浅埋隧道围岩压力和破坏机制的影响, 从而指导类似实际工程的安全施工。

1 破坏模式与速度场

采用极限分析理论来研究浅埋隧道的围岩稳定性问题时, 必须要先假定临界破坏形状。根据已有的研究成果, 浅埋隧道和深埋隧道的区别主要在于埋深, 而关于破坏形状, 则表现为破坏面是否会延伸到地表面。根据已有的破坏机制[11–16], 本文引入了浅埋隧道的破坏机制与速度场(图1)。如图1所示, 隧道洞径为, 埋深为。在施工过程中, 浅埋隧道发生破坏, 破裂面、延伸到地表面, 拱顶上方岩体以0的速度竖直运动, 速度间断线、以01的速度朝洞内运动, 破坏刚体、以速度1朝洞内运动, 破裂角为。所有速度与破坏面夹角均为内摩擦角, 且假定洞室边缘的围岩压力荷载均匀分布, 压力荷载为。

(a) 破坏机制          (b) 速度场

2 求解过程

2.1 基本假定

对浅埋隧道围岩的稳定性进行分析计算时, 作了以下假设: (1) 破坏模式当做二维的平面应变问题进行分析研究; (2) 将破坏体视为体积不变的刚性破坏块体; (3) 采用矩形横截面对圆形洞室进行计算。

2.2 围岩压力

由于破坏机制是对称的, 故取隧道破坏的一半进行分析计算, 以减少分析过程中的计算量。

如图1(b)所示, 根据构建的速度场, 可以得到各间断线的速度分别为:;。由图1(a)可得各间断线的长度和破坏体的面积分别为:,,;,。

采用极限分析定理对浅埋隧道围岩进行分析时, 首先要计算重力和支护力产生的外力功率和破坏过程中速度间断线上产生的能量耗散。其计算的具体表达式分别为: 土体的重力功率,P=00+11cos(+); 洞室支护反力功率,P=-0–1cos(π/2 ––); 速度间断线上的能量耗散,P=0cos+01cos+1cos。

根据虚功率原理, 外力功率和能量耗散相等, 即可以得到围岩压力的上限解析解

根据图1(b)可得, 变量的几何边界条件为:

(2)

那么, 在几何边界条件式(2)下, 求解式(1)中围岩压力的最大值, 即为围岩压力的最优上限解。

3 结果分析

3.1 单一参数变化对浅埋隧道围岩稳定性的影响

采用极限分析上限法研究不同单一参数对浅埋隧道稳定性的影响, 其围岩压力与破坏模式的变化规律如图2～9所示。其中参数取值: 洞径= 10 m; 埋深= 20 m; 土体容重= 20 kN/m3; 黏聚力= 10 kPa; 内摩擦角= 18°。

图2 埋深比对围岩压力的影响

图3 埋深比对破坏机制的影响

图4 重度对围岩压力的影响

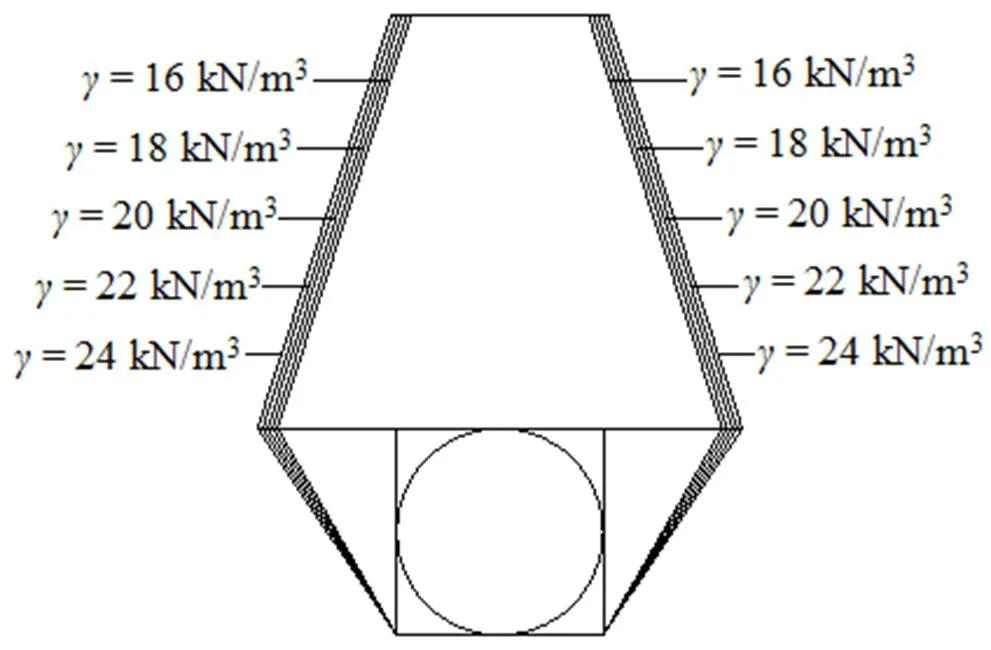
图5 重度对破坏机制的影响

图6 黏聚力对围岩压力的影响

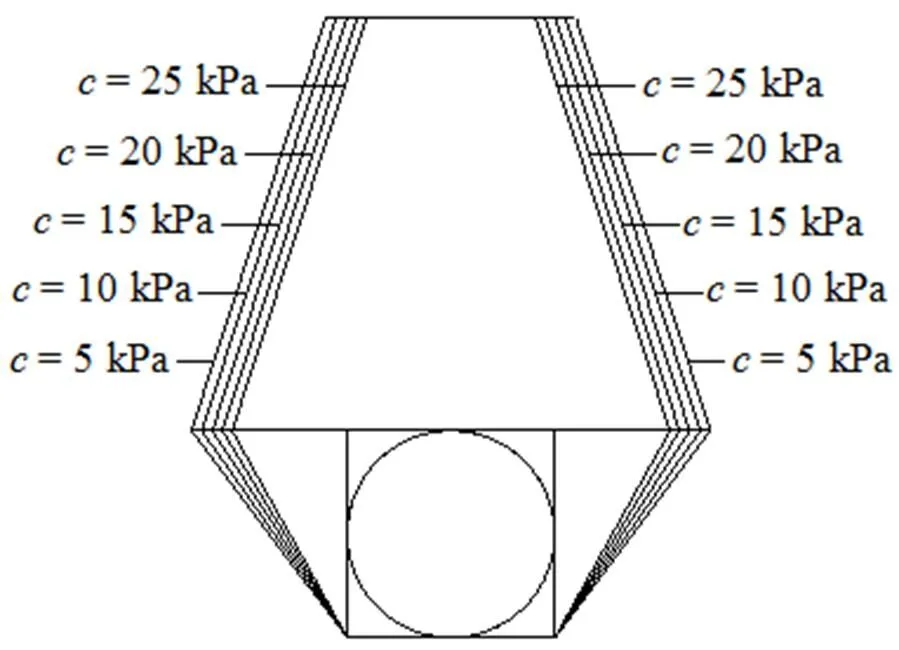
图7 黏聚力对破坏机制的影响

图8 内摩擦角对围岩压力的影响

图9 内摩擦角对破坏机制的影响

由图2可知, 埋深比的增大会导致浅埋隧道的围岩压力增大, 即当隧道洞径固定不变时, 隧道埋深增大, 浅埋隧道围岩压力增大。由图3可知, 埋深比的增大会导致浅埋隧道的破裂面向外扩展, 即当隧道洞径固定不变时, 随着隧道埋深的增大, 土体的自稳能力变差, 产生塑性区的范围变大, 浅埋隧道的破裂面向外扩展。因此, 对于埋深较大的浅埋隧道应采用更安全可靠的支护措施, 防止发生垮塌事故。

由图4可得, 当隧道围岩重度增大时, 浅埋隧道的围岩压力亦增大。根据图5可知, 当隧道围岩重度增大时, 浅埋隧道的破裂面向外扩展。因此, 对于围岩重度较大的浅埋隧道应采取更为安全可靠的支护措施, 防止发生垮塌事故。

由图6可得, 当黏聚力增大时, 浅埋隧道的围岩压力减小。根据图7可知, 当黏聚力减小时, 隧道的破裂面向外扩展, 即黏聚力越大, 土体的自稳能力将会越强, 隧道的支护反力、破坏范围就会越小。对于围岩较差的浅埋隧道应采取更为安全可靠的支护方案, 防止发生垮塌事故。

由图8可得, 内摩擦角越大, 浅埋隧道洞室的围岩压力越小。由图9可得, 随着内摩擦角的增大, 浅埋隧道的破裂面收缩, 即内摩擦角变大, 土体的自稳能力增强, 隧道的支护反力以及破坏范围减小。故对于内摩擦角较小地段的浅埋隧道应采取更为安全可靠的支护方案, 以防止发生垮塌等安全事故。

3.2 软弱围岩对浅埋隧道稳定性的影响

针对Ⅴ级或以下软弱围岩, 假定5组不同的围岩参数, 采用极限分析上限法研究不同埋深比下浅埋隧道破坏时的围岩压力以及破坏范围, 其中5组软弱围岩物理力学性质参数如表1所示。

表1 软弱围岩物理力学性质参数

由图10知, 随着软弱围岩参数的增大, 浅埋隧道围岩压力减小; 而随着埋深比的增大, 浅埋隧道围岩压力增大, 但针对参数相对较好的第1组围岩, 当埋深比增大到一定值时, 由于围岩较好, 埋深较大, 围岩的自稳能力较强, 则浅埋隧道不会发生破坏。在埋深比为2的情况下, 图11示出了5组不同软弱围岩下浅埋隧道的破坏范围。由图11可知, 随着软弱围岩参数的增大, 浅埋隧道破坏范围减小。所以, 针对埋深较浅、围岩较差的浅埋隧道, 应该加强支护措施。

图10 软弱围岩参数对围岩压力的影响

图11 软弱围岩参数对破坏机制的影响

4 结论

(1) 针对软弱围岩的浅埋隧道, 采用极限分析上限法得到了围岩压力的解析表达式, 并且采用序列二次迭代算法得到了围岩压力的优化解和优化后的破坏模式。

(2) 针对浅埋隧道的稳定性问题, 分析了单一参数对围岩压力和破坏面的影响。若埋深越大、土体容重越大、黏聚力越小以及内摩擦角越小, 则浅埋隧道的围岩压力越大, 破坏范围也越大。讨论了Ⅴ级或以下软弱围岩浅埋隧道的稳定性, 当埋深较大、围岩较好时, 由于自稳能力, 浅埋隧道有可能不会发生破坏, 相反, 则应该加强支护措施, 防止发生垮塌事故。

参考文献：

[1] 谢骏, 刘纯贵, 于海勇. 双平行圆形隧道稳定的塑性极限分析上限解[J]. 岩石力学与工程学报, 2006, 25(9): 1835– 1841.

[2] Yang X L, Huang F. Slope stability analysis considering joined influences of nonlinearity and dilation [J]. Journal of Central South University of Technology, 2009, 16(2): 292–296.

[3] Yang X L, Sui Z R. Seismic failure mechanisms for loaded slopes with associated and nonassociated flow rules [J]. Journal of Central South University of Technology, 2008, 15(2): 276–279.

[4] 伍良波, 刘运思. 不同埋深比下浅埋隧道稳定性的上限分析[J]. 公路工程, 2013, 38(4): 262–264.

[5] Yang X L, Zou J F. Cavity expansion analysis with non-linear failure criterion [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2011, 164(1): 41–49.

[6] Yang X L. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948–953.

[7] Yang X L. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion [J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46–56.

[8] Yang X L, Zou J F. Stability factors for rock slopes subjected to pore water pressure based on the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1 146–1 152.

[9] 许敬叔, 潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报, 2014, 11(4): 80–84.

[10] 王路路, 潘秋景. 三级台阶边坡稳定性分析的上限解研究[J]. 铁道科学与工程学报, 2013, 10(3): 43–46.

[11] Yang X L, Huang F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686–691.

[12] Yang X L, Wang J M. Ground movement prediction for tunnels using simplified procedure [J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462–471.

[13] Yang X L. Seismic passive pressures of earth structures by nonlinear optimization [J]. Archive of Applied Mechanics, 2011, 81(9): 1 195–1 202.

[14] Yang X L, Yin J H. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505–511.

[15] Yang X L. Seismic bearing capacity of a strip footing on rock slopes [J]. Canadian Geotechnical Journal, 2009, 46(8): 943–954.

[16] Yang X L, Yin J H. Upper bound solution for ultimate bearing capacity with a modified Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 550–560.

[17] Yang X L, Li L, Yin J H. Seismic and static stability analysis for rock slopes by a kinematical approach [J]. Geotechnique, 2004, 54(8): 543–549.

[18] Yang X L, Yin J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267–273.

[19] Yang X L, Huang F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 189–195.

[20] 严若明, 周光裕, 唐金. 浅埋隧道塌方机理上限分析[J]. 铁道科学与工程学报, 2014, 11(5): 96–99.

(责任编校: 江河)

Energy analysis of stability of shallow tunnel in weak surrounding rock

Chen Honglin, Wu Wei, Shu Xinwen

(Yonglong Expressway Construction and Development Co Ltd, Jishou 416700, China)

From the viewpoint of energy, the stability of shallow tunnel is analyzed based on the upper bound theorem of limit analysis. The expression of surrounding rock pressure and the position of failure surface are obtained by calculating. Result shows that the surrounding rock pressure and the region of the collapsing block increases with the increasing of buried depth and unit weight of soil mass, however it decreases with the increasing of cohesion and internal friction angle. Moreover, it can also be found that the tunnel with a higher buried depth and a better characteristic of surrounding rock mass is not easy to collapse. While a more reliable supporting measure should be taken in the excavating tunnel in poor surrounding rock so as to keep from collapsing.

shallow tunnel; weak surrounding rock; upper bound theorem of limit analysis; earth pressure; failure scope

10.3969/j.issn.1672–6146.2015.04.016

U 451

1672–6146(2015)04–0075–05

陈洪林, chl_hn@163.com。

2015–07–28

湖南省永龙高速公路建设开发有限公司资助课题(1228)。