复合优化问题的Lagrange全对偶

龚鑫, 方东辉



复合优化问题的Lagrange全对偶

龚鑫, 方东辉

(吉首大学数学与统计学院, 湖南吉首, 416000)

在函数不一定下半连续的情况下, 利用次微分的性质, 引进新的约束规划条件, 刻画了复合优化问题的稳定全对偶, 并把相关结论应用于复合锥规划的研究之中, 推广了前人的相关结论。

复合优化; 稳定全对偶; 复合锥规划

约束优化问题是优化理论中的重要课题之一, 受到了有关学者的广泛关注。特别地, 许多学者研究了经典的凸约束优化问题[1–6], 建立了一系列有关凸约束优化问题的对偶理论,类最优性条件等。例如, 文献[1]借助共轭函数上图技巧引入了一类新的正则条件, 等价刻画了一类特殊的复合凸优化问题的稳定强对偶性、全对偶性及逆对偶性。文献[2]研究了凸约束优化问题的强对偶、全对偶等, 而文献[3]在函数不具有连续性的假设下, 利用次微分性质, 等价刻画了凸约束优化问题的全对偶和最优性条件。

由于许多优化问题, 例如凸约束优化问题、极大极小问题、锥规划等, 都可以看成复合优化问题的特例, 因此, 复合优化问题的对偶理论引起了学者们的广泛关注[7–11]。本文在上述文献的基础上, 研究如下复合优化问题:其中,是实局部凸Hausdorff拓扑向量空间,是的非空凸子集,是中的闭凸锥,是一个指标集(可能是无限集),是真函数且是–凸函数, (是关于偏序下的最大元),是真凸函数且关于是递增的,是真凸函数。

本文在函数不一定下半连续, 集合不一定是闭集的假设下, 研究复合凸优化问题的全对偶。利用函数的次微分性质, 引进新的约束规范条件, 建立了Lagrange稳定全对偶和全对偶成立的充分和/或必要条件。由于凸约束优化问题是问题的特例, 因此本文推广了凸优化中的相关结论。

1 预备知识

设,是实局部凸Hausdorff拓扑向量空间,和是和的共轭空间, 分别赋予弱拓扑和。表示泛函在的值, 即。非空集合的示性函数和对偶锥分别定义为。记且仅有有限多个。

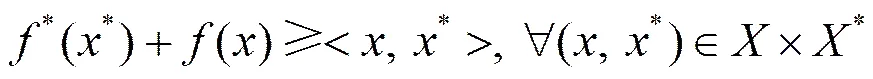
当且仅当。 (2)

2 Lagrange全对偶

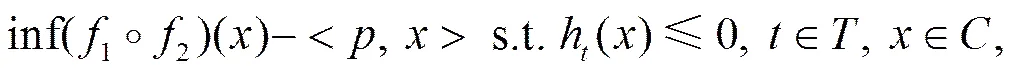
。 (5)

故式(7)成立当且仅当

。 (9)

。 (12)

由定理1可得如下推论。

3 复合锥规划中的应用

(15)

。 (17)

设

则由定理1和推论1可得如下结论。

参考文献：

[1] Li C, Fang D H, Lopez G, et al. Stable and total Fenchel duality for convex optimization problems in locally convex spaces [J]. SIAM J Optim, 2009, 20: 1 032–1 051.

[2] Li C, Ng K F, Pong T K. Constraint qualifications for convex inequality systems with applications in constrained optimization [J]. SIAM J Optim, 2008, 19: 163–187.

[3] Fang D H, Li C, Ng K F. Constraint qualifications for optimality conditions and total Lagrangian dualities in convex infinite programming [J]. SIAM J Optim, 2010, 73: 1 143–1 159.

[4] Fang D H, Li C, Ng K F. Constraint qualifications for extended Farkas's lemmas and Lagrangian dualities in convex infinite programming [J]. SIAM J Optim, 2009, 20: 131–132.

[5] Li C, Ng K F, Pong T K. The SECQ linear regularity and the strong CHIP for infinite system of closed convex sets in normed linear spaces [J]. SIAM J Optim, 2007, 15: 643–666.

[6] Goberna M A, Jeyakumar V, Lopez M A. Necessary and sufficient conditions for solvability of systems of infinite convex inequalities [J]. Nonlinear Anal, 2008, 68: 1 184–1 194.

[7] Lemaire B. Application of a subdifferential of a convex composite functional to optimal control in variational inequalities [C]// Nondifferentiable optimization: motivations and applications(Sopron, 1984). Berlin: Lecture Notes in Econom and Math Systems 255, 1985: 103–117.

[8] Zhou Y Y, Li G. The Toland-Fenchel-Lagrange duality of DC programs for composite convex functions[J]. Numerical Algebra Control and Optimization, 2014, 4: 9–23.

[9] 赵丹, 孙祥凯. 复合凸优化问题的稳定强对偶[J]. 吉林大学学报(理学版), 2013, 51(3): 441–443.

[10] 孙祥凯. 复合凸优化问题全对偶性的等价刻画[J]. 吉林大学学报(理学版), 2015, 53(1): 33–36.

[11] Zalinescu C. Convex Analysis in General Vector Spaces [M]. New Jersey: World Scientific, 2002.

(责任编校:刘晓霞)

Lagrangian total duality of the composite optimization

Gong Xin, Fang Donghui

(College of Mathematics and Statistics, Jishou University, Jishou 427000, China)

Under the assumption that the functions are not necessary continuous, the total duality and the stable total duality between the composite problem and its dual problem are established by using the properties of subdifferentials. And its applications to the composite conical optimization problem is also given. The results extend the corresponding results in the previous papers.

composite optimization; the stable total duality; composite conical optimization

10.3969/j.issn.1672–6146.2015.04.001

O 221.6

1672–6146(2015)04–0001–04

方东辉, dh_fang@163.com; 龚鑫, 15225396406@163.com。

2015–09–06

国家自然科学基金项目(11461027);湖南省优秀青年科研项目(13B095);湖南省研究生创新科研基金资助项目(CX2015B548);吉首大学校级科研项目(13JDY040)。