具有最小压缩功的氢网络优化设计

邓春，周宇航，周业扬，冯霄



具有最小压缩功的氢网络优化设计

邓春1，周宇航，周业扬1，冯霄2

（1重质油国家重点实验室，中国石油大学（北京）化学工程学院，北京 102249；2西安交通大学化学工程与技术学院，陕西 西安，710049）

炼油厂用氢装置多在高压下操作，为此配置有很多新氢和循环氢压缩机用于提升氢气流股的压力，从而消耗大量的压缩功，同时大量地增加了炼油厂的操作费用。因此，氢网络的优化，除了需要优化氢气公用工程的用量，减少整个网络的压缩功也十分重要。本文借鉴邻近算法的思想，进一步考虑压力约束，提出了改进邻近算法以及压力-浓度图，能够设计具有最小压缩功的氢网络。案例分析所求得的最小压缩功为16.435 MJ，压缩机数目为9个，比文献优化结果减少两个。

过程系统；优化设计；氢；图示法；压缩功；邻近算法；

引 言

重质劣质原油的加工比例不断增加，以及环境法规的愈发严格，促使炼油厂增加加氢催化裂化、加氢精制等工艺过程的比例，致使炼油厂耗氢量剧增。然而，为了达到油品标准中的芳烃含量的要求，催化重整等产氢装置的加工量不断减少。产氢量的降低和耗氢量的增加形成了强烈的反差，炼油厂氢气的亏缺加剧。因此，能够有效地提高氢气利用率，节约氢气消耗，实现节能降耗，一直是研究的热点。通常，氢网络优化的方法主要有两类：氢夹点法[1-3]和数学规划法[4-12]。

炼油厂用氢单元对氢气流股的氢气纯度和杂质浓度均有一定的要求。此外，氢气流股的压力也要求高于用氢单元的压力条件。因此，炼油厂有很多新氢和循环氢压缩机，用于提升氢气流股的压力，从而消耗大量的压缩功，同时也增加了氢气分配网络的操作费用。Ding等[13]提出利用平均压力-流量图判断局部系统是否需要添置压缩机，然而并未给出确定最小的压缩功的系统化方法。Bandyopadhyay等[14]提出一种精确确定氢气分配网络最小压缩功的方法。该方法将具有多个压力等级的氢气分配网络分解为多个具有两个压力等级的子网络，进而通过最小化压力等级之间的流率而最小化压缩功。然而，压力等级之间的流率的最小值需要采用Sahu和Bandyopadhyay[15]提出的代数法。此法意义明确，但是其繁琐程度随氢气分配网络的压力等级数的增加而增大。

邻近算法（nearest neighbor algorithm, NNA）[16]已经广泛应用于仅考虑浓度约束的水[2,16-18]和氢气分配网络[2,19]的设计。结合Bandyopadhyay等[14]提出的计算最小压缩功的方法，本文拟提出改进的邻近算法，考虑压力约束，以设计具有最小压缩功的氢气分配网络。

1 问题描述

给定一个氢气分配网络，包括一些用氢单元。它们的出口流股可看做一系列的过程氢源（ÎNSR），入口流股则作为一系列的过程氢阱（ÎNSK）。每一股过程氢源具有一定的流率（SRi）、杂质浓度（SRi）和压力（SRi）。每一个过程氢阱有一定的入口流率（SKj）、最高入口杂质浓度限制（）和入口压力要求（SKj）。部分过程氢源可以直接/提纯回用或者提升压力以满足过程氢阱的需求，多余的不能回用的过程氢源则排放至燃料系统。另外，可能需要外部新鲜氢源（例如氢气公用工程）作为补充，其杂质浓度为HU，压力为HU。本文旨在利用改进的邻近算法设计具有最小压缩功的氢气分配网络。

2 压缩功的统一表达式

压缩功由流股流经压缩机前后状态（流率和压力）所决定的。对于等温压缩过程，压缩功的表达式如方程（1）所示

对于等温过程有=常数。因此等温压缩过程的压缩功表达式可以用方程（2）表示

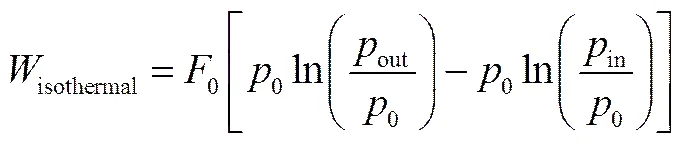
其中，下标0表示标况。in和out分别为压缩机的入口和出口压力。Bandyopadhyay等[14]提出将和分别改写为out和in，定义为压缩过程的压力指数[14]。

对于绝热/多变压缩过程，有=常数。其中为绝热/多变指数。于是绝热/多变压缩功的表达式可由式（3）和式（4）表示

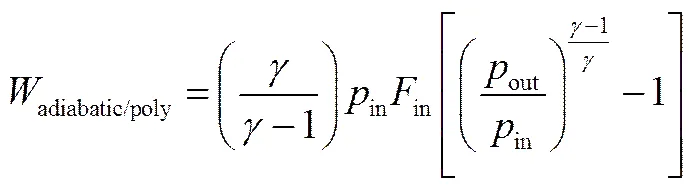
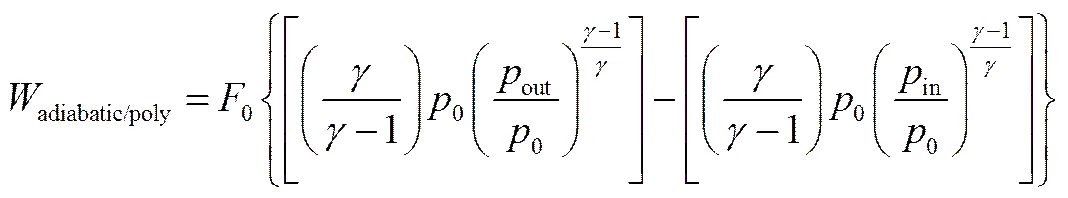
其中，Bandyopadhyay等[14]提出将和改写为out和in。

于是，压缩功的表达式可以统一表达为

=(out-in) (5)

其中

3 改进的近邻算法

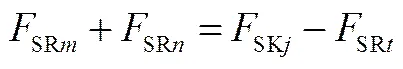
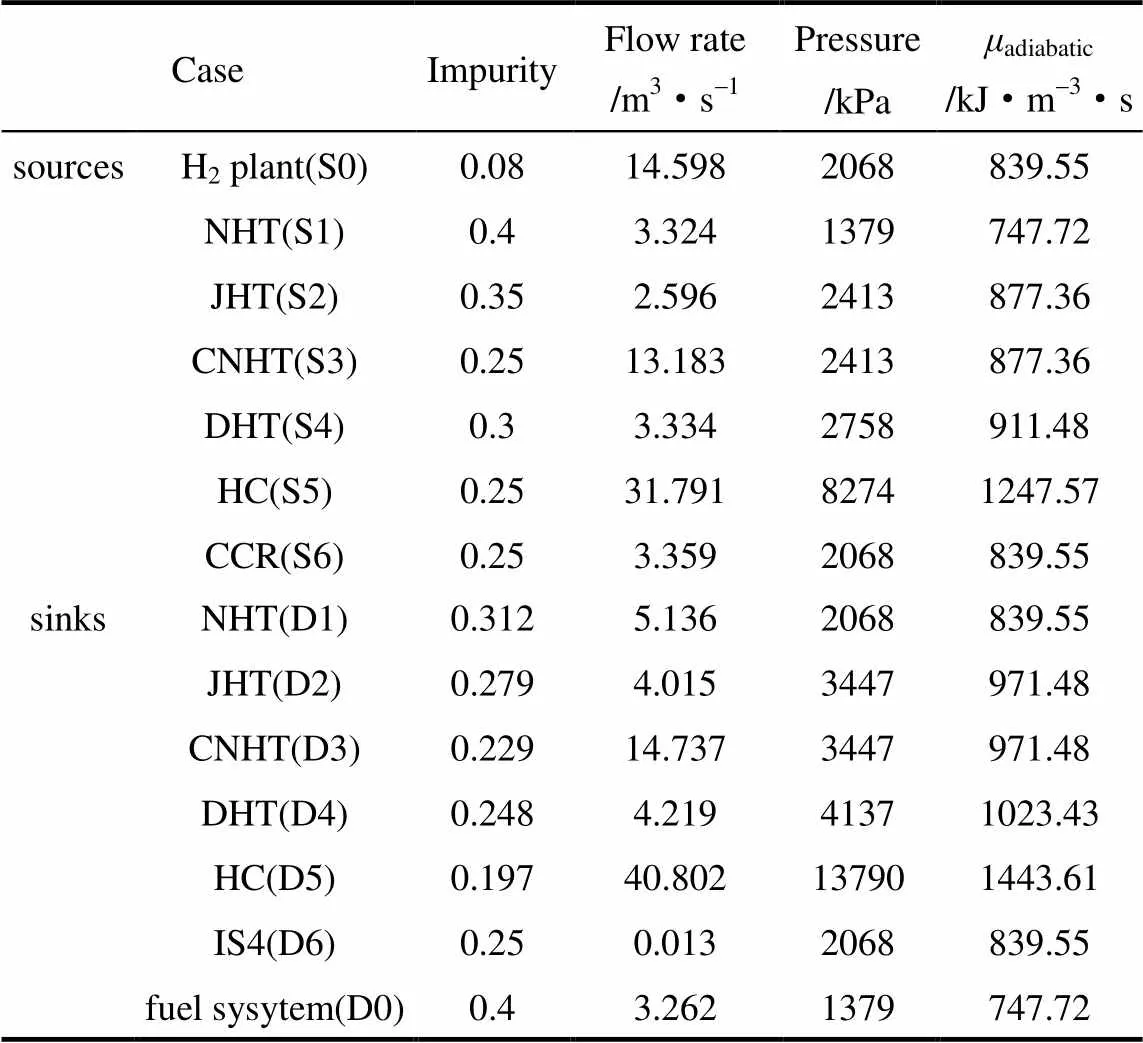
借鉴Bandyopadhyay等[14]提出的计算最小压缩功的方法，结合邻近算法的思想，本文提出改进的邻近算法用以设计最小压缩功的氢气分配网络。另外，本文还提出压力-浓度图以辅助改进的邻近算法的实施。具体步骤为：（1）确定氢阱的匹配次序：按照压力等级从高到低，压力相同时按照杂质浓度从低到高的顺序对氢阱进行排序。（2）氢阱的最高入口杂质浓度限制和压力要求分别为和SKj，首先选择杂质浓度相同的氢源（），若压力满足条件SKt≥SKj，则压缩功为零。若压力满足条件SKt

4 案例研究

氢气分配网络的极限数据提取自文献[4]，如表1所示。首先利用夹点法[1-3,19-20]确定该网络最小的氢气公用工程用量。本文采用改进的问题表法[19]，最小的氢气(标准状态)公用工程用量为14.6m·s-1，记为S0，CCR装置的用量为3.36 m3·s-1，排放至燃料系统的流股杂质浓度为0.4（体积分数，下同），流率为3.26 m3·s-1，记为D0。然后根据方程（6）计算氢源氢阱的压力指数，为了与文献[14]进行比较，本文计算绝热压缩过程的压力指数，见表1的第6列。

下面举例介绍提出的改进邻近算法的实施步骤。首先按照步骤（1）确定氢阱的匹配次序为：D5，D4，D3，D2，D6，D1，D0；然后利用步骤（2）和（3）依次对氢阱进行匹配。例如，氢阱D4（流率为4.219 m3·s-1，杂质浓度上限为0.248，压力为4137 kPa）的匹配，按照传统的邻近算法，应该选择杂质浓度为0.08（氢源S0）和0.25的氢源来满足。而杂质浓度为0.25的氢源有S5（8274 kPa）、S3（2413 kPa）和S6（2068 kPa）。传统的邻近算法并未考虑压力约束，只能随便选择其中的一个来满足D4的需求。而本文提出的改进的邻近算法则会优先选择其中压力最高的S5，流率不足再选择压力较高的S3，最后再选择S6。求解式（7）和式（8），计算出具体的流率分配为S0：0.05 m3·s-1，S5：3.71 m3·s-1, S3：0.458 m3·s-1。氢阱D4的匹配关系如图1所示，其中需要升压的流股加粗以示区别。

表1 案例的氢气极限数据 Table 1 Limiting hydrogen data for case study

由方程（5）可知，绝热压缩功等于绝热压力指数差乘以流率。例如：从S5到D5的流股，需要升压，其流率为28.081 m3·s-1，而绝热压力指数差为196.04 kJ·(m3·s-1)-1。所以绝热压缩功=（28.081 × 196.04）kJ=5505 kJ。整个网络的绝热压缩功可以计算得到为16.435 MJ。

最后根据图1进行压缩机的配置。需要注意的是，并不是每一股升压的流股都需要配置压缩机。例如，从S0到D3和D2的流股都是从1379 kPa升压到3447 kPa；S6到D3和D2的流股都是从2068 kPa升压到3447 kPa。只需分别配置一个压缩机即可。最后得到的带有压缩机的氢气分配网络如图2所示。总压缩机数为9个，比文献[14]少两个。与文献[14]的网络进行比较，文献中CCR供给DHT的流股在本文的网络中则是供给CNHT，但是这个流股分配的变化不影响压缩功的计算，而网络其他部分与文献[14]一致。所以最小压缩功应该与文献[14]一致，但是最终计算结果（16.435 MJ）高于文献[14]的结果（15.09 MJ），分析文献[14]可知，首先文献[14]中S4的压力（2767.9 kPa）与原始文献[4]不一致，其次氢气公用工程量的最小值（14.61 m3·s-1）与本文优化得到的结果（14.598 m3·s-1）不同，导致计算所得的氢源氢阱之间的分配流股的流率值有误差，最终使得结果数值有了差异。

5 结 论

本文结合邻近算法的思想，考虑压力约束，提出改进的邻近算法，用以设计具有最小压缩功的氢气分配网络。另外，提出压力-浓度图以辅助改进的邻近算法的实施。在压力-浓度图上，利用所提出的改进邻近算法的详细步骤，进行最小压缩功的计算和压缩机配置的分析，并对压缩机进行合并。最后设计出具有最小压缩功的氢气分配网络。本文利用改进的邻近算法分析案例得到最小压缩功为16.435 MJ。另外因为本文考虑了压缩机的合并，压缩机个数比文献[14]中的减少了两个。

符 号 说 明

c——杂质浓度 F——流率，m3·s-1 HU——氢气公用工程 NSK——过程氢阱 NSR——过程氢源 p——压力，kPa μ——压力指数，kPa g——绝热/多变指数

References

[1] Alves J J, Towler G P. Analysis of refinery hydrogen distribution systems [J]., 2002, 41(23): 5759-5769.

[2] Agrawal V, Shenoy U V. Unified conceptual approach to targeting and design of water and hydrogen networks [J]., 2006, 52(3): 1071-1082.

[3] Foo D C Y, Manan Z A. Setting the minimum utility gas flowrate targets using cascade analysis technique [J]., 2006, 45(17): 5986-5995.

[4] Hallale N, Liu F. Refinery hydrogen management for clean fuels production [J]., 2001, 6(1): 81-98.

[5] Liu F, Zhang N. Strategy of purifier selection and integration in hydrogen networks [J]., 2004, 82(A10): 1315-1330.

[6] Liao Z, Wang J, Yang Y, Rong G. Integrating purifiers in refinery hydrogen networks: a retrofit case study [J]., 2010, 18(3): 233-241.

[7] Jia N, Zhang N. Multi-component optimisation for refinery hydrogen networks [J]., 2011, 36(8): 4663-4670.

[8] Wu S, Liu G, Yu Z, Liu Y, Deng C. Optimization of hydrogen networks with constraints on hydrogen concentration and pure hydrogen load considered [J]., 2012, 90(9): 1208-1220.

[9] Zhou L, Liao Z, Wang J, Jiang B, Yang Y. Hydrogen sulfide removal process embedded optimization of hydrogen network [J]., 2012, 37(23): 18163- 18174.

[10] Deng C, Pan H, Lee J Y, Foo D C Y, Feng X. Synthesis of hydrogen network with hydrogen header of intermediate purity [J]., 2014, 39(25): 13049- 13062.

[11] Deng C, Pan H, Li Y, Zhou Y, Feng X. Comparative analysis of different scenarios for the synthesis of refinery hydrogen network [J]., 2014, 70(2): 1162-1179.

[12] Deng Chun(邓春), Zhou Yeyang(周业扬), Chen Jie(陈杰), Feng Xiao(冯霄). Optimization of inter-plant hydrogen system with purification reuse in petrochemical complex [J].(化工学报), 2014, 65(12): 4914-4920.

[13] Ding Y, Feng X, Chu K H. Optimization of hydrogen distribution systems with pressure constraints [J]., 2011, 19(2/3): 204-211.

[14] Bandyopadhyay S, Chaturvedi N D, Desai A. Targeting compression work for hydrogen allocation networks [J]., 2014, 53(48): 18539-18548.

[15] Sahu G C, Bandyopadhyay S. Mathematically rigorous algebraic and graphical techniques for targeting minimum resource requirement and interplant flow rate for total site involving two plants [J]., 2012, 51(8):3401-3417.

[16] Prakash R, Shenoy U V. Targeting and design of water networks for fixed flowrate and fixed contaminant load operations [J]., 2005, 60(1): 255-268.

[17] Shenoy U V. Enhanced nearest neighbors algorithm for design of water networks [J]., 2012, 84: 197-206.

[18] Deng C, Feng X. Targeting for conventional and property-based water network with multiple resources [J]., 2011, 50(7): 3722-3737.

[19] Deng C, Zhou Y, Chen C, Feng X. Systematic approach for targeting interplant hydrogen networks [J]., 2015, 90(1): 68-88. DOI:10.1016/ j.energy. 2015.05.054.

[20] El-Halwagi M M, Gabriel F, Harell D. Rigorous graphical targeting for resource conservationmaterial recycle/reuse networks [J]., 2003, 42(19): 4319-4328.

Optimal design of hydrogen network with minimum compression work

DENG Chun1，ZHOU Yuhang1，ZHOU Yeyang1，FENG Xiao2

（1；2School of Chemical Engineering and Technology, Xi’an Jiaotong University, Xi’an 710049, Shaanxi, China）

Hydrogen consuming units in refineries are operated in high pressure, thus some makeup hydrogen and recycle hydrogen compressors are utilized to increase the pressure of hydrogen streams. It leads to a large increase on compression work and operating cost. Therefore, except for the minimizing the flowrate of hydrogen utility, it is extremely important to reduce the compression work when optimizing hydrogen network. In this paper, based on the concept of the nearest neighbors algorithm, pressure constraints are taken into consideration, a novel nearest neighbors algorithm as well as pressure-impurity concentration diagram are proposed to design hydrogen network with minimum compression work. The results for the case study show that the minimum compression work achieves 16.435 MJ, and the number of compressor is nine which is two less than that in the literature.

process systems; optimal design; hydrogen; graphical approach; compression work; nearest neighbors algorithm

2015-09-06.

DENG Chun, chundeng@cup.edu.cn

10.11949/j.issn.0438-1157.20151393

supported by the National Basic Research Program of China(2012CB720500), the National Natural Science Foundation of China (U1162121,21276204) and the Science Foundation of China University of Petroleum, Beijing (2462015YQ0305).

TQ 021. 8

A

0438—1157（2015）12—4883—05

国家重点基础研究发展计划项目（）；国家自然科学基金项目（U1162121，21276204）；中国石油大学（北京）科研基金项目（2462015YQ0305）。

2015-09-06收到初稿，2015-09-30收到修改稿。

联系人及第一作者：邓春（1984—），男，博士，副教授。